公交加气站选址布局优化模型和算法

魏明，陈学武，孙博

（1.东南大学城市智能交通江苏省重点实验室，南京210096；2.南通大学交通学院，江苏南通226019）

公交加气站选址布局优化模型和算法

魏明*1,2，陈学武1，孙博2

（1.东南大学城市智能交通江苏省重点实验室，南京210096；2.南通大学交通学院，江苏南通226019）

针对不同线路的车辆加气需求在时间和空间上的不平衡性，将加气站抽象为多服务台排队系统，综合考虑车辆行驶、排队加气、加气站的位置对公交运营的影响等现实因素，以加气站的建设费用最小为第一目标，以极小化所有公交车的加气成本为第二目标，建立一种多目标公交加气站选址模型.根据问题特征，利用约束法，将之转化为单目标问题，设计求解该问题的遗传算法，定义解的编码方案、适应度函数、产生初始种群的启发式算法等.最后，结合一个算例，计算最佳的公交加气选址方案，分析加气站的能力对其布局的影响程度，从而验证模型和算法的有效性.

城市交通；加气站选址；车辆排队加气；多目标；遗传算法

1 引言

城市居民出行在时间和空间上不均衡，以及时疏散乘客为目标，必须统筹与之相匹配的线网密度、车队规模及其运营计划，因而各线路在不同时段利用其客流的高平锋间隙满足它们显著差异的加气需求.若公交加气站的建设规模及布局缺乏科学规划，造成部分加气站数量不足导致车辆排起长龙，不能及时返回车场按计划正常运营；而部分加气站数量过多或布局不当，出现土地资源浪费、加气成本上升等问题[1，2].因此，针对多线路车辆的加气需求在时空分布上的特征，如何合理布设公交加气站的规模与数量，显得尤为重要.

该问题为公交加气站选址布局问题（Bus Gas Station Site Layout Problem，BGSSLP），与天燃气(Compressed NaturalGas，CNG)加气站布点问题类似，均属于组合优化的NP-Hard问题，前者研究较为少见，而后者吸引了众多国内外学者的关注.前者研究可借鉴后者的研究思路，主要有二：

首先，科学计算最佳CNG加气站选址方案，该研究较少，童岱等采用定性分析与定量计算相结合的方法综合探讨了CNG优化布局选址方法[3]；Am ir等人研究车辆进入CNG加气站的排队特征并给出布局优化方法[4]；赵涛等人研究模拟退火算法在天然气加气站选址中的应用[5]；吴芳构建了一类城市CNG加气站布点优化模型[6]；黄海波等根据最短路径理论建立了加气站和车站车源分配模型[7].

其次，评价CNG加气站布点的合理性，这方面研究相对成熟，已经在该领域综合运用模糊数学、色关联分析等[8-11]方法，并开发软件推广应用[12].

由上可知，现有研究没有考虑加气站的通行能力对其布局的影响，也未涉及加气站的布局如何影响公交运营.

针对现有研究的不足，本文考虑加气站的选址布局对公交运营的影响，将车辆在加气站的补充燃料排队过程抽象为多服务台排队系统，以追求加气站建设费用和车辆加气成本最少为目标，建立了多目标公交加气站选址布局优化模型，并设计求解该问题的遗传算法.最后，通过一个实例计算最佳的公交加气选址方案，分析加气站的能力对其布局的影响程度，检验本研究的有效性.

2 问题描述及数学模型

某区域总共有S个站场和M个候选加气站地点.每个站场∀s∈S经营Rs条线路，对每条线路∀j∈Rs，在时间段离开站场去气站加气的车辆数为nj.根据公交运营的时间约束，这些车辆在加气站的排队时间均不超过一定时间T，要求它们在时间段内必须返回站场.每个候选地点∀i∈M的土地经济费用为ci元、停车能力约束为li，可购置yi个加气设备（其费用为p元），每台设备给车辆加气的平均时间为o小时.站场∀s∈S和候选地点∀i∈M之间距离为ds,i≤D（D为车辆的最大行驶距离），车辆在两地之间行驶速度为vs,i，单位运输费用为r元.线路∀j∈Rs（∀s∈S）的唯一加气站点为φ(j)，φ(φ(j),i)表示φ(j)是否为候选地点∀i∈M.线路∀j∈Rs的车辆一次完整加气时间为Tj=2ds,φ(j)/vs,φ(j)+o+ΔTj，包括行驶时间加气时间o和平均等车时间ΔTj≤T.所有车辆在各个加气站∀i∈M的车辆排队长度为Li≤li.xi表示某个地点∀i∈M是否被选为加气站.

将加气站抽象为一个多服务台排队系统，按先进先出原则，假设车辆到达加气站服从泊松分布和服务时间为负指数分布，根据各个站场不同线路的车辆加气需求在时间和空间上的不平衡性，确定某个地点是否被选为加气站，以及其加气设备的数量，考虑最大行驶里程、排队长度和等车时间等现实约束，追求加气站的建设费用和所有公交车的加气成本最小.

综上所述，本文的数学模型如下：

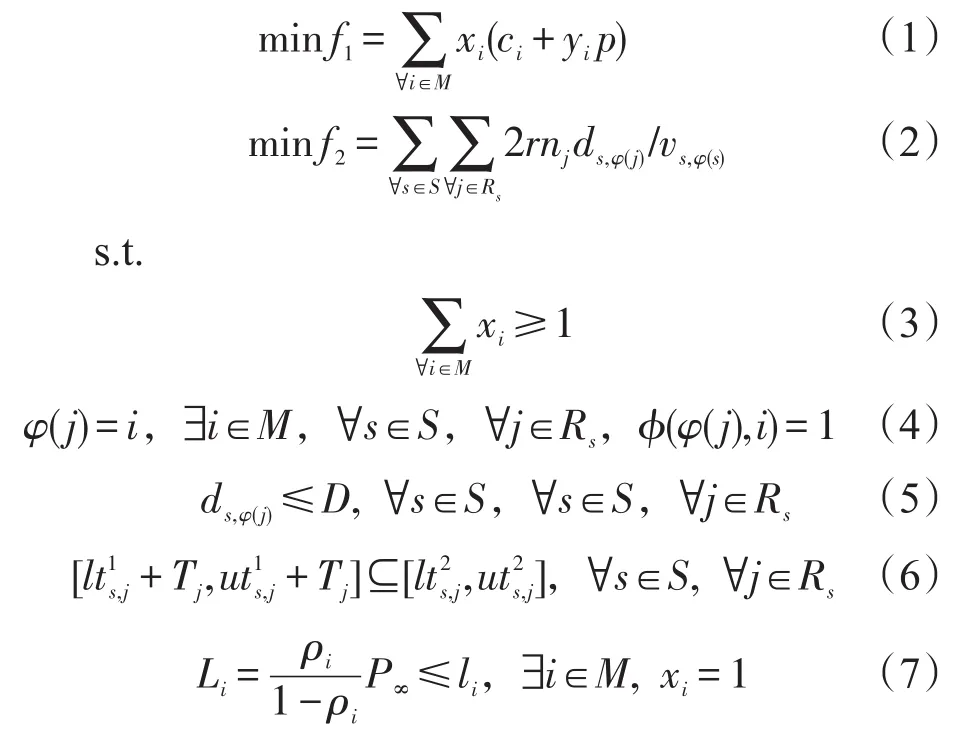
在上述模型中，式(1)–式(2)是问题的目标函数.式(1)表示极小化公交加气站的建设管理费用；式(2)表示各个站场的车辆去附近加气站的运行成本最少.式(3)–式(8)是约束条件.式(3)表示至少建设一个加气站；式(4)确保任意线路都能在附近加气站补充燃料；式(5)表示站场和加气站之间距离小于一定距离；式(6)限制公交车从站场出发后完成加气的返回时间；式(7)表示加气站的服务能力约束；式(8)表示车辆在加气站排队等候加气的平均时间小于一定值；式(9)表示两个决策变量的0–1和整数约束.

3 求解BGSSLP的遗传算法

由上可知，BGSSLP属于任务分配问题范畴，为一类NP难题[9].针对很难于构建BGSSLP的高效启发式算法的缺陷，文中利用遗传算法(Genetic A lgorithm,GA)[13]求解BGSSLP，借鉴GA求解该复杂问题的通用框架，根据问题特征，定义解的编码方案、适应度函数、产生初始种群的启发式算法等，其详细过程如下.

3.1 编码方案

采用自然数编码方式,用向量X=(x1,x2,...,xM)表示一个解的染色体，元素xi≥0为候选地点i的加气设备数量，若xi=0，则该候选站点未被选中.由上可知,任意X都遵守约束式(3)，对∃xi≠0，基于贪婪规则确定(∀s∈S,∀j∈Rs)φ(j)=i，将X解码为各个加气站服务的站场集合，若它满足约束式(5)–式(9)，则X对应一个可行解.

例如：染色体X=[1 0 1 0 0 0 3 0]蕴含8个候选站点，1、3和7候选站点被选中，它们建设加气设备的数量为1、1和3.

3.2 适应度函数的设计

在现实中，交通部门投入建设气站费用一般是有限的.因此，以f2为主目标，将f1转为约束，构造BGSSLP的单目标规划模型[14].

其它约束与原来的相同.式(11)表示交通部门投资建设公交加气站的总费用不超过一定值c，其中c由政府预算决定.由式（10）推导可知，加气站点的总数量取值在一定范围内.

本文以Fit(f)=f2为适应度函数，利用其评价个体的好坏，求解BGSSLP的非劣解.

3.3 产生初始种群的启发式算法

BGSSLP的影响因素众多，随机产生的个体很难满足全部约束，初始种群的质量不高影响GA的求解效率.因此，构造启发式算法求得不同可行个体，具体步骤如下.

步骤1根据S个站场的坐标位置，遵从约束式（5），利用聚类算法，将它们划分为K个子区域S=(S1,S2,…,SK).设置c'=0.令k=1，转向步骤2.

步骤2对每个子区域Sk，查找可行的候选加气站集合Vk，转向步骤3.

步骤3从Vk中随机选择加气站i，计算车辆到达率决定ΔTj、Li，根据li和T确定yi的下限根据约束式（11）确定yi的上限随机产生个体X的基因转向步骤4.

步骤4对Sk的全部加气需求，若加气站i的设备满足约束式（6）–式（8），转向步骤5；否则，根据约束式（4），基于贪婪原则将Sk的剩余加气需求并入相邻子区域，或单独作为一个子区域，转向步骤5.

步骤5令k=k+1，若k≤K，转向步骤2；否则，算法终止，输出可行个体X.

显然，根据上述启发式算法获取的个体都是BGSSLP的可行解.

3.4 遗传操作

遗传操作包括选择、交叉和变异，其中选择运算采用轮盘赌选择法和精英保留法组合的策略，从父代种群中优选出下一代个体；交叉运算采用单点交叉策略，以一定概率选择交叉点，交换一组染色体对应基因段，产生一组新解；变异运算直接使用基本位变异策略，依据变异概率，判断个体的每一个基因座是否为变异点，并对之做相关运算，进而产生出新个体.

显然，交叉和变异操作可能破坏解的可行结构，舍弃这些新产生的不可行个体.

3.5 终止原则

种群完成预先给定的进化代数.

4 算例分析

某城市区域有14个站场和10个候选加气地点，其网络拓扑结构如图1所示，不同站场经营21条线路在加气高峰时段的最大需求如表1，候选地点的基本信息如表2，其它参数为p=50 000元/个、T=10m in、D=6 km、o=5m in和r=22元/h.

图1 站场和候选地点的网络拓扑结构Fig.1 Network topology network topology between busand gas stations

在MATLAB中，利用Sheffield的GA工具箱函数编写求解BGSSLP的仿真程序，设置相关参数为迭代次数10 000、染色体数100、交叉率0.7和变异率0.05，在政府预算c=3 800 000情形下计算机运行实例10次，获得该问题的最优气站布局方案如表3所示，从表中可知：针对21条线路在加气高峰时段的时空分布需求，总投资3 650 000元，建设5个加气站和购买13套加气设备，这些线路的128辆车加气运营费用为741.8元，共行驶579 km，其用时2 845.4m in（等车时间占14.84%）.

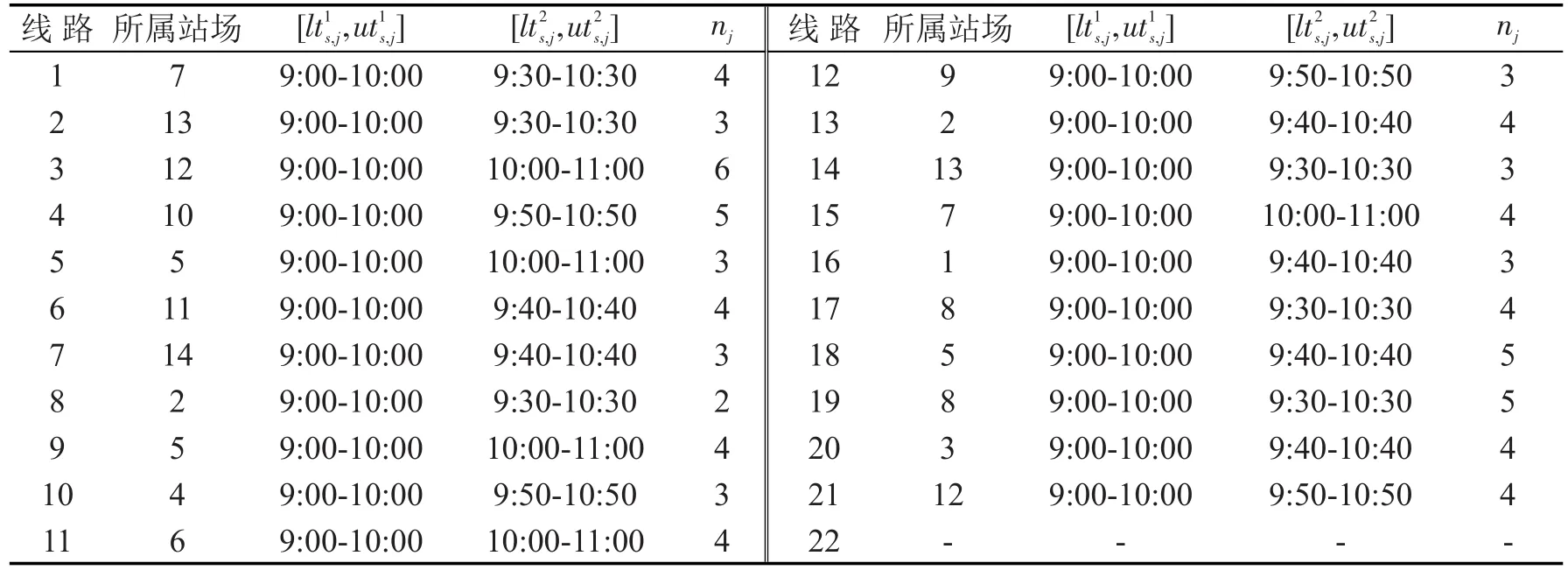
表1 各线路在加气高峰时段的最大需求Table 1 The num ber ofeach line's fuelling vehicles in aerated peak periods

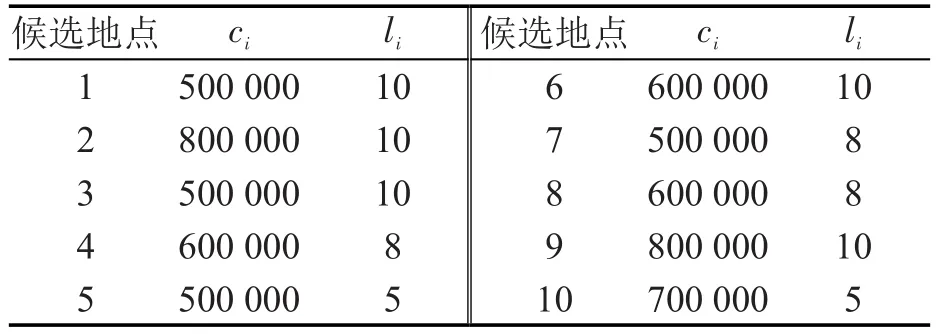
表2 候选地点的基本信息Table 2 Basic information of candidate gas stations

由上可知，当某加气站的公交车到达率较高时，若其服务水平低，此时加气站的服务强度较大，致使车辆等待时间（排队长度）较长，各线路的车辆在加完气后可能不能按规定时间返回车场.虽然增加一定数量的加气设备数可以缩短车辆运营时间，这确保为下一阶段的公交运营提供运力支撑，但与加气设备的使用率矛盾，故综合考虑公交运营、加气站的通行能力和加气设备闲置之间最佳联系，计算结果和直观分析一致.

此外，考察c、D和T对BGSSLP的影响，如表4和表5所示，从表中可知：

（1）当加气设备数不低于某值时才满足所有车辆的加气需求，随着c的变小，布局方案偏向于ci较小的候选地点或减少加气站数，这可能引起空驶距离增大，故f1和f2分别逐步变小和变大.

表3 最优公交加气站选址布局方案Table 3 Optim al layoutscheme for bus gas stations

表4 不同c的最优公交加气站选址布局方案Table 4 Optimal layoutscheme for bus gas stations under differentvalues of c

（2）随着D的变小，各个加气站辐射公交站场的范围缩小，必须增加一定数量的公交站点才满足所有车辆的加气需求，因而所有车辆在站场和气站之间总行驶里程减少，故f1和f2分别逐步变大和变小.

表5 不同D的最优公交加气站选址布局方案Table 5 Optim al layoutschem e for bus gas stations under differentvalues of D

（3）随着T的变小，进一步限制了车辆在某气站的等待时间，与该气站的服务水平ρi相关，取决于其车辆到达率λi和服务率yiμi，因而增加一定数量加气设备或调整部分线路的加气需求至相邻气站（相对较远），故f1和f2均逐步变大.

表6 不同T的最优公交加气站选址布局方案Table 6 Optimal layoutscheme for bus gas stations under differentvalues of T

5 研究结论

本文考虑加气站的选址布局对公交运营的影响，将车辆在加气站的补充燃料排队过程抽象为多服务台排队系统，研究一种多目标公交加气站选址布局优化模型及其求解算法，它可计算一个适于需求时空分布不均匀的最佳公交加气站选址布局方案.该研究对城市公交加气站的建设规模及布局具有一定的指导意义.

但是本文将公交和出租车分开讨论，没有考虑随机到达的出租车的加气需求影响公交车补充燃料，仅研究公交加气站的选址布局问题，若集成它们于一体，加气站的能力是动态变化的；另外，文中假设随机干扰不影响车辆正常运行，随机旅行时间的BGSSLP更具有实际价值，这类BGSSLP将是今后进一步研究的方向.

[1]David A，Jenny K．Parking demand and responsiveness to supply，pricing and location in the Sydney central business district[J].Transportation Research Part A, 2001,35(1):177-196．

[2]Larson R C．A Hypercube queuing model for facility location and redistricting in urban emergency services[J]. Computersand OperationsResearch,1974,56(1):67-95．

[3]童岱,殷国富,骆勇,等.天然气汽车加气站优化布点方法初探[J].四川工业学院学报,2002,21(4):17-19.[TONG D,YIN G F,LUO Y,et al.An initial probe into the optimal layout of CNG station in a city[J]. Sichuan University of Science and Technology,2002,21 (4):17-19.]

[4]Amir A S,Meysam H,Farshid A.Hybrid systems modeling in non standard queue and optimization with the simulation approach in CNG stations[J].Research Journal of Applied Sciences,Engineering and Technology,2012,4(14):2110-2119.

[5]赵涛,夏雨.模拟退火算法在压缩天然气加气站选址中的应用[J].价值工程,2010,29(10):121-122. [ZHAO T,XIA Y.The application of simulated annealing algorithm in layout of CNG filling stations[J]. Value Engineering,2010,29(10):121-122.]

[6]吴芳,马昌喜,李志成.城市CNG加气站布点优化的混合粒子群算法仿真[J].交通运输系统工程与信息,2011,11(5):134-139.[WU F，MA C X，LI Z C.Simulation of hybrid particle swarm algorithm for optimizing urban compressed natural gas station arrangement[J].Journal of Transportation Systems Engineering and Information Technology,2011,11(5): 134-139.

[7]黄海波,殷国富.城市CNG汽车加气站布点计算机辅助评价方法[J].天然气工业,2004,24(2):93-96. [HUANG H B,YIN G F.Computer aided evaluation method for layout of urban CNG filling stations[J]. NaturalGas Industry,2004,24(2):93-96.]

[8]徐晋,梁冠民.基于模糊层次分析法的CNG加气站选址研究[J].交通科技与经济,2011,65(3):82-84. [XU J,LIANG G M.Based on fuzzy analytic hierarchy process of CNG fueling station location research[J].

Technology&Economy in Areas of Communications, 2011,65(3):82-84.]

[9]侯晓,张鹏,陈利琼.基于模糊综合法的加气站风险评价研究[J].天然气与石油,2009,27(5):14-17. [HOU X,ZHANG P,CHEN L Q.Study on risk evaluation of CNG filling station based on fuzzy comprehensive evaluation method[J].Natural Gas and Oil,2009,27(5):14-17.]

[10]陈杰,石超,方来华.基于灰色关联分析和IAHP的CNG加气站安全评价方法研究[J].中国安全科学学报,2009,19(6):159-164.[CHEN J,SHIC,FANG L H.Study on safety evaluation of CNG filling station based on the grey correlation method and IAHP[J]. China Safety Science Journal,2009,19(6):159-164.]

[11]王琢玉.城市LPG加气站规划布局评价方法研究[J].城市公共交通,2006,5(2):217-230.[WANG Z Y.Study on the evaluation methods for the layout of urban LPG stations[J].City Transportation,2006,5(2): 217-230.]

[12]尹燕莉.CNG加气站安全评价技术研究及软件开发[D].西华大学，2004.[YIN Y L.Software development and safety evaluation study of CNG filling station[D].Xihua University,2004.]

[13]雷英杰,张善文,李续武,等.Matlab遗传算法工具箱及应用[M].西安：西安电子科技大学出版社, 2005,62-94.[LEIY J，ZHANG SW，LIX W,et al．MATLAB genetic algorithm toolbox and its applications[M].Xian：Xidian University Press,2005:62-94.]

[14]《现代应用数学手册》编委会.现代应用数学手册:运筹学与最优化理论卷[M].北京：清华大学出版社,2004,318-323.[Modern application math manual editorial board.modern application math manual operational research and optimization theory[M]. Beijing:Tsinghua University Press,2004,318-323.]

Model and Algorithm for Bus Gas Station Site Layout Optimization Problem

WEIM ing1,2,CHEN Xue-wu1,SUN Bo2

(1.Jiangsu Key Laboratory of Urban ITS,SoutheastUniversity,Nanjing 210096,China; 2.Schoolof Transportation,Nantong University,Nantong 226019,Jiangsu,China)

For the imbalance in time and space of refueling vehicleswhich belonged to different routes,a multiple objective model is studied for bus gas station site layout optim ization to meet many realistic constraints such as vehicle’s travel,lining up to fuelatgas station,and influence of gas station’s location on bus operation,etc.,by assuming that each gas station is looked as amulti-server queuing system.Previous objective is tom inimize a total of cost for building gas stations,and secondary objective aims atminimizing fueling fee for all vehicles.According to characteristic of themodel,it is converted into a single objective programming problem with constraintmethod.A design of genetic algorithm,which redesigns a solution coding,heuristic procedure to initialize chromosomes random ly,etc.,is proposed to obtain themodel’s noninferior solutions.Finally,a numerical example is taken to calculate itsbestscheme and analyze influence of gasstation’s fueling capacity on them,which showsmodeland itsalgorithm’correctnessand effectiveness.

urban traffic;gas station site layout;all vehicles queuing for fueling at stations;multiple objective;genetic algorithm

1009-6744（2015）03-0160-06

TP301.6，U116.2

A

2014-09-05

2015-01-15录用日期：2015-03-11

国家重点基础研究发展计划（973计划）资助项目(2012CB725402)；中国博士后科学基金面上项目（2013M540408）；江苏省高校自然科学研究面上项目(13KJB580008).

魏明(1984-)，男，安徽芜湖人，讲师，博士后.＊通信作者：mingtian911@163.com