基于谱分析的路段行程时间多步预测方法

邓明君，曲仕茹，秦鸣

（1.西北工业大学自动化学院，西安710072；2.华东交通大学土建学院，南昌330013）

基于谱分析的路段行程时间多步预测方法

邓明君*1，2，曲仕茹1，秦鸣2

（1.西北工业大学自动化学院，西安710072；2.华东交通大学土建学院，南昌330013）

路段多步行程时间预测数据是动态交通诱导系统的重要参数，但已有研究成果，大多集中于一步预测，且存在适应性不强、计算量大、基础数据需求多等不足.应用谱分析及Karhunen-Loeve（K-L）变换对历史及当前检测行程时间序列进行分解与重构，重构时以历史序列与当前检测序列的欧式距离作为相似性度量指标，优化重构时的特征向量系数，使与当前检测序列相似度高的历史序列信息在重构中占据主要地位，通过重构，实现对后续若干时段的行程时间的预测，实测数据检验显示该方法可实现多步预测，预测精度良好，较以往方法有所提高，且历史数据需求量小，计算量小.

城市交通；行程时间；多步预测；Karhunen-Loeve变换；时间序列重构

1 引言

路段行程时间是交通诱导方案生成的重要基础参数，但道路上的交通状态瞬息万变，直接用当前检测数据制定下一时刻的交通管控方案，会产生方案滞后于实际交通状态的结果.若预先估算出将来某个时段的路段行程时间，并以此制定诱导方案，则方案的实时性提高，有利于合理选择出行路径.当前该方向的成果大致分为两类，一类是基于统计的方法，如非参数回归、卡尔曼滤波和小波模型.第二类为智能学习模型,如模糊预测、遗传算法和神经网络等[1，2].但这些方法均存在无法体现交通流的动态性，需要历史数据量大，具有一定的滞后性等不足,且这些模型多以单步预测为主，尽管文献[3，4]提出了2种行程时间多步预测方法，但这两种方法仍然存在预测值滞后、数据需求量大的缺憾.

信息理论中的频谱分析方法可以揭示隐含在随机序列中的趋势信息，从而实现对随机信号的估计.1974年Nicholson[5]，第一次将谱分析法应用于交通流量预测，他将随机流量序列表示为若干正交向量的线性组合，用最小二乘法确定组合系数，建立了流量预测模型.虽然这一方法具有较高的预测精度，但需实时修正组合系数，计算量大，应用困难，文献[6]将该方法程序化，并能够完成多步预测，但该方法没考虑历史数据与当前数据间的相关性，信息挖掘不充分，文献[6]的验证结果显示，平均一步预测误差为11%.进一步研究历史数据与当前数据的相关性可能是提升谱分析预测精度的一个思路.本文在文献[5，6]基础上，通过优化特征向量系数，使历史序列中，更符合当前交通变化趋势的序列在预测中得到更多的权重表达，并采用时间窗滚动方法实现多步预测.

2 谱分析原理

谱分析方法是将随机序列分解为不同振幅、相位、频率的序列组合，通过分解发现随机序列的主要变化规律，从而实现对随机序列的估计.应用于谱分析的变换有多种，其中离散Karhunen-Loeve (K-L)变换是以随机序列统计特征为基础的在均方意义下为最佳的正交变换.该变换只要较少个数的系数就能恢复出精度不错的原随机序列.

将M维间隔为k,k=1,2,…,N的离散随机序列定义为

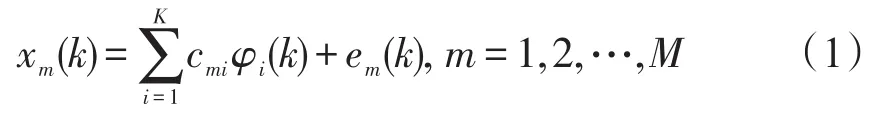
式中xm(k)表示M维序列中第m个序列在第k个时间间隔时的值；em(k)为该时刻的误差；φi(k)为一组正交向量；cmi为对应的正交向量系数.

由于K-L变换的能量集中性，式（1）中i的取值可做K步截断,i=1,2,…,K.即在有限的K项分解下，式（1）右侧就可很好地逼近xm(k).

式（1）中正交向量有如下性质：

式中δij为Kronecker对角阵.

将式（1）用向量表示：

因为φTφ=I，可得特征向量系数矩阵：

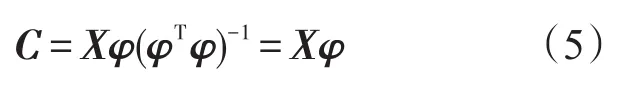
C中的每一个元素相互独立，且对应于用于预测的互不相关的一个基.Davenport[7]发现可以用离散形式的K-L积分方程来表示随机序列协方差矩阵的分解，如式（6）所示.

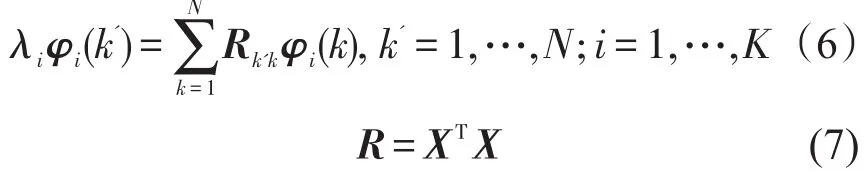
式（6）求得特征向量矩阵φ及对应的特征根λ，将λ由大到小排列，由K-L变换能量集中性，用部分较大特征根对应的特征向量，通过重构便能恢复出随机序列的主要信息.将不同时段检测的路段行程时间看作是一组随机序列X，求得系数C后，结合特征向量矩阵φ，由式（3）可反求时间序列Xˉ.上述方法能够实现对历史数据序列的再现，但预测问题不是历史数据的重现，而是要从历史数据中挖掘出对预测有用的信息以指导预测.路段交通特性显示，同一路段相同工作日的交通特性具有相似性，因此融合历史数据序列的相似性，则有可能得出符合当前数据变化规律的结果.

3 基于谱分析的多步行程时间预测方法

3.1 基于谱分析法行程时间预测的优化思路

统计历史上某道路某工作日IT分钟间隔的平均行程时间序列值，全天共计组数据，连续统计S周，获得一个S×F的矩阵，由式（5）～式（7）求得S×K维的系数矩阵Ch及对应的特征向量矩阵φ.用当前检测序列构造一个新序列Xc用以计算当前序列特征向量系数Cc，Xc=(T1,T2,…,Tt,Tt+1,Tt+2,…,Tt+b)，其中，T1～Tt为当前检测序列，Tt+1～Tt+b为对应时刻历史序列均值，由式（5）求得1×K维系数向量Cc，将Ch与Cc加权合并，得1×K维系数加权和向量Cv，Cv=WC，其中，W为组合权重向量.优化组合权重便可达到历史数据、当前检测数据最优融合的目的.

3.2 cv合成时的权值优化

ch蕴含了该序列的波动信息，为预测准确，那些与当前序列波动更为相似的序列应提供更多信息，为体现这一原则，以当前序列与对应历史序列值之间的欧氏距离来描述其相似性.设当前检测值与各历史序列对应值的欧氏距离为d(i)，则Ch中各行的权重向量：

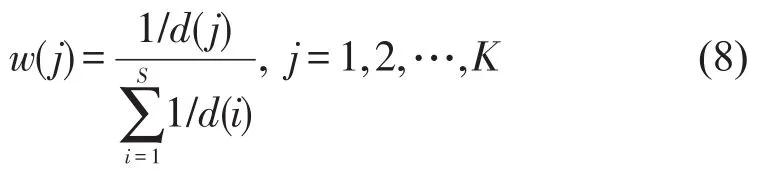
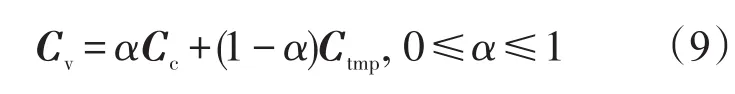
假设在一个适当的时段内，当前检测序列与历史综合序列对待估序列的影响权重具有延续性，则可以通过回朔当前已检测的若干连续时段的预测值与其对应检测值的误差平方和最小来确定α，而在下一步预测中延续这种组合，并在每次获得检测值后，计算预测误差，当预测误差超过设定阈值ε后，则重新优化α，设回朔时段为a,得优化问题模型.

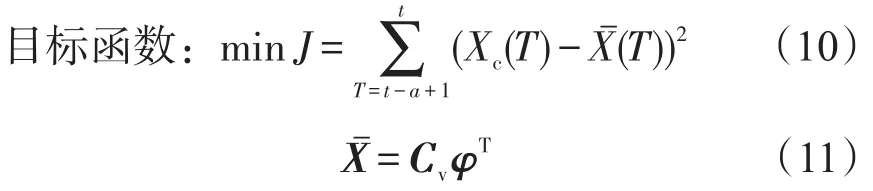
结合式（9）的条件，构成一个带约束的二次优化问题，决策变量为α，对于二次优化问题求解，一类方法是消去约束，用数值计算方法求解，另一类方法是采用智能计算方法求解.数值计算法对目标函数及约束条件要求严格，某些时候可能无法求解，而智能计算方法不基于理论推导，求解条件相对宽松，给定学习终止条件，总可以在给定区域找到最优或局部最优解，因此本研究采用粒子群算法，以式（10）目标函数为适应度函数，约束条件为粒子的取值范围，用式（12）对粒子的速度和位置进行更新，并设定终止迭代条件，当前后两次迭代的差值小于某一个给定阈值θ，或迭代次数达到某设定阈值G，则终止迭代，输出α的优化值.

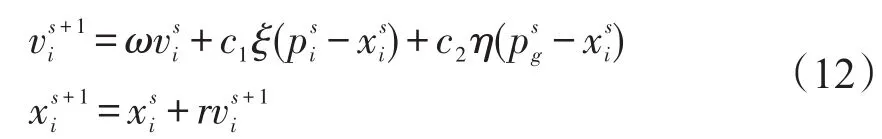
计算步骤：

Step 1随机生成满足约束条件的一定数量的粒子个体；

Step 2依据目标函数，计算每个粒子的适应度，并更新每个粒子历史最优适应度值对应的位置信息及全局最优适应度粒子对应的位置信息；

Step 3依据式（12）对各粒子的速度和位置进行更新；

Step 4转至Step2，并判断是否终止，以输出最优值；

Step 5得出α最优值，由式（9）计算Cv，并进行下一步预测计算.

3.3 多步预测及滚动

距离当前时间越近的时段，其之间的相关性越强，为减少不必要的计算，在多步预测中，只考虑当前时段之前的a个时段及之后的b个时段的数据，通过对特征向量矩阵φ的滚动来实现这一目标.即在求特征向量系数Ch和Cc时，选取特征向量

3.4 预测方法应用流程

通过上述分析，总结基于谱分析的行程时间多步预测流程如下：

（1）给定回朔时段a和预测步数b,读入S天同一工作日的历史序列矩阵X，求其协方差矩阵及特征根和特征向量.

（2）以历史序列计算特征向量系数Ch.

（3）依据各天历史序列与当前检测序列的欧式距离计算组合特征向量系数Ctmp，用当前检测序列计算Cc.

（4）根据前一步预测误差e是否超过误差阈值ε，确定是否需要更新α，是则转（5），否则转（6）.

（5）用粒子群算法确定回朔时段内Cc与Ctmp的组合权重α.

（6）用α和Cc、Ctmp计算最终特征向量系数Cv.

（8）计算预测误差e，时间推进一步，转（3）.

4 验证分析

利用南昌市洪都大桥连续六周，星期二的行程时间作为验证数据，行程时间为检测间隔内通过检测路段所有车辆行程时间的均值.关于检测时间间隔大小，对预测精度也有一定影响，当间隔较短时，序列的波动性变大，而对于波动性较大的序列，预测时需要准确描述其高频特性，因此在相同精度条件下需要更多特征向量来重建，即需要更大的截断值K,从而增加计算量.文献[6]验证，当间隔为15m in时，谱分析法的综合性能最好，因此用15m in间隔行程时间数据进行验证.其中前五周的数据作为历史数据，第六周的数据为检验数据.分别选取不同回朔时段a及预测步长b进行预测，选取平均相对误差、均方根相对误差作为评价指标分析预测效果.在Matlab平台上，实现本文方法，输出的各指标如表1所示.

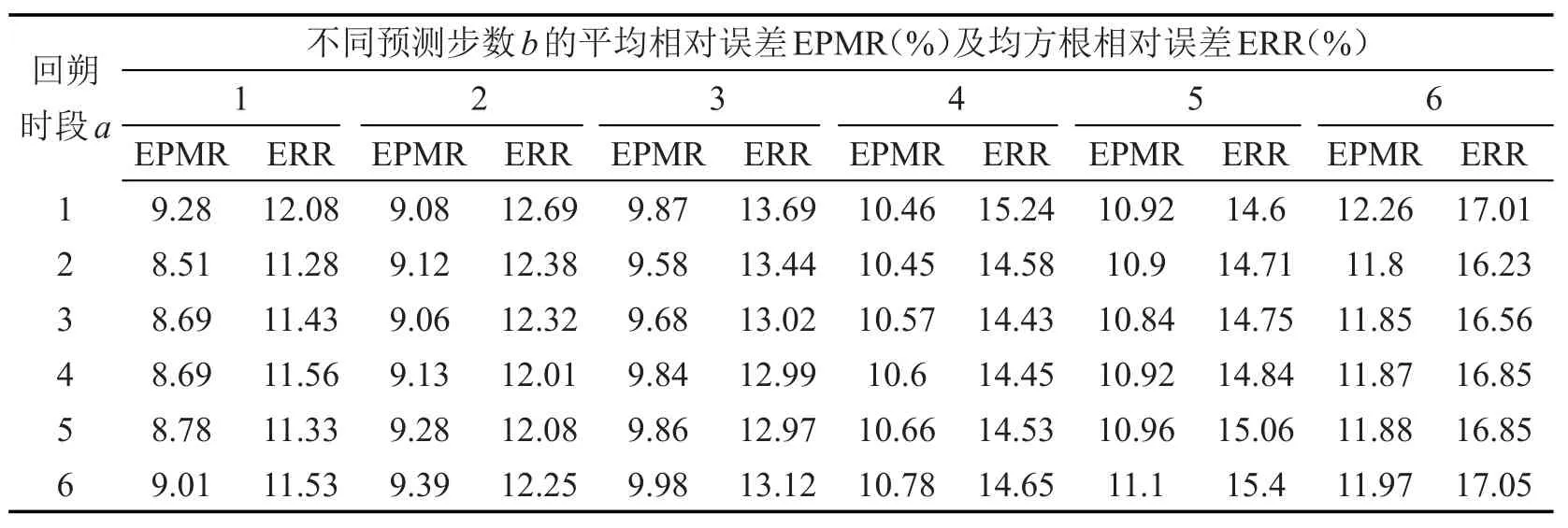
表1 不同时间窗下预测的相对误差与均方根误差Table 1 EPMR and ERR ofsome difference time w indow w idth

分析可见，当回朔时段数是2时，各指标数据相对较好，绘制回朔时段为2的多步预测曲线，为使各线条清晰，只绘制1～3步及实测值等四条曲线.

利用本次检测数据，应用文献[6]方法预测，就预测平均相对误差、均方根相对误差与本文方法进行对比，如表2所示.

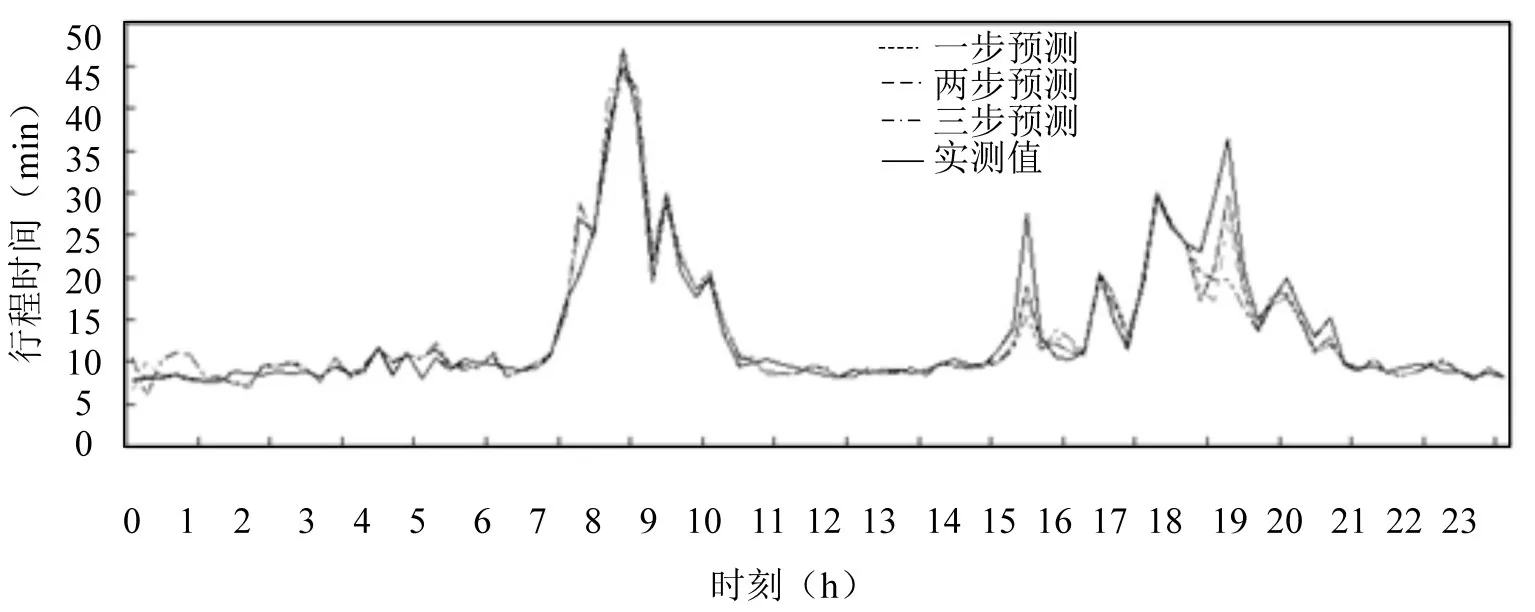
图1 1～3步预测与实测值对比图Fig.1 Comparison chartof1～3 step forecastingand detection

表2 本文方法与文献[6]方法预测效果对比表Table 2 The performance of this describes and reference[6]

由表2可知，本文方法预测结果略好于文献[6]方法，说明应用欧式距离进行权重优化，可提高谱分析方法在时间序列预测时的精度.

分析相对误差分布，分别以5%、10%、20%、30%、40%、60%、100%作为统计区间，累计误差分布数，如表3所示.

表3 各步预测误差统计表Table 3 The statistics ofeach step prediction

表3显示，各步长预测误差在10%以内的时刻分别占了总时刻数的70.83%、65.63%、63.54%.1～4步预测中，本方法60%以上的时刻，各步预测误差均小于10%，对于随机性很强的交通系统来说，10%以内的误差基本可以满足交通控制及诱导需求.

5 研究结论

将谱分析中的分解与重构思想应用于短时行程时间预测，仅需要较少的对应时段的历史数据，计算效率高，且能实现多步预测.从预测精度来看，一步预测的相对误差为8.51%，三步预测的相对误差为9.58%，从预测误差分布来看，四步以内，60%以上的预测值，误差在10%以内.与当前短时交通预测方法相比,谱分析方法不存在卡尔曼滤波等线性估计方法预测值滞后的不足，也没有神经网络等智能学习方法所必须的大量训练和预测精度受泛化性能影响的局限，具有较好的综合实用价值，当然该方法也存在一些弱点，如在求协方差矩阵的特征向量和特征根时，如果维度过高则求解困难，甚至无解，所以该方法的序列划分长度不能太长.

参考文献：

[1]G A Davis,N L Nihan.Nonparametric regression and short-term freeway traffic forecasting[J].J.Transp.Eng., 1991,117(2):178-188.

[2]张玉梅，曲仕茹，温凯歌.基于混沌和RBF神经网络的短时交通流量预测[J].系统工程，2007,25(11):26-32. [ZHANG YM，QU SR，WEN K G.A short-term traffic flow forecastingmethod based on chaos and rbf neural network[J].Systems Engineering,2007,25(11):26-32.]

[3]李进燕,朱征宇,刘琳.基于简化路网模型的卡尔曼滤波多步行程时间预测方法[J].系统工程理论与实践, 2013，33（5）:1289-1297.[Ll JY,ZHU ZY,etal.Multi step Kalman filtering travel time estimation method based on simplified road network model[J].Systems Engineer Theory&Practice,2013,33(5):1289-1297.]

[4]李琦,姜桂艳.SCATS线圈数据短时多步双重预测方法[J].哈尔滨工业大学学报,2 013,45(2):123-128.[LIQ,JIANG G Y，Bi-levelmethod ofmulti-step forecasting for short-term data of loop in SCATS[J]. Journal of Harbin Institute of Technology,2013,45(2): 123-128.]

[5]H Nicholson,C D Swann.The prediction of traffic flow volumes based on spectral analysis[J].Transport Res., 1974,8:533-538.

[6]Tigran T Tchrakian,Biswajit Basu,et al.Real-time traffic flow forecasting using spectral analysis[J].Ieee Transactions on Intelligent Transportation Systems, 2012,13(2):519-526.

[7]W BDavenport,W LRoot.An introduction to the theory of random signals and noise[M].New York:McGraw-Hill,1958.

SpectralAnalysis App lied in Road Travel Time MultiStep Prediction

DENGM ing-jun1,2,QU Shi-ru1，QINm ing2

（1.Schoolof Automatic Control,Northwestern PolytechnicalUniversity,Xi′an 710072,China；2.Schoolof CivilArchitecture, EastChina Jiaotong University,Nanchang 330013,China）

Road multi interval travel time forecasting data is an important parameter for dynam ic traffic guidance system.But previously developed models have some deficiency,such as bad adaptability,large amountof calculation needing andmany history data requirement.Applied the decomposition,reconstruction of spectral analysis and Karhunen-Loeve(K-L)transform method to decompose and reconstruct the history and currentdetection travel time series.Euclidean distance is used tomeasure the closeness between current and historical travel time series,by themeans of optim ization the eigenvector coefficient tomake thosemore closely history series has themore weight in the reconstruction and then gain the goal of road travel time multi step forecasting.The case study suggest that,the proposed method can fulfillmulti step road travel time prediction and has a good prediction accuracy,some better than the previousmethod,furthermore,a fewerhistory dataand calculation resourcesneeding.

urban traffic；travel time；multi-step prediction；Karhunen-Loeve transform；time series reconstruction

1009-6744（2015）03-0134-06

U491.4

A

2014-09-16

2015-04-30录用日期：2015-05-04

江西省自然科学基金（20142BAB201015）；江西省科技厅科技计划项目（20123BBE50094）.

邓明君（1978-），男，陕西略阳人，讲师，博士.＊通信作者：dmstd98@163.com