浅谈解数学题的策略

陈海彦

（铜川矿务局第一中学）

解数学题时，一般先经过思考、类比、联想应用所学的数学概念、定理公式等为依据是提高分析问题、解决问题的能力，加快解决速度的重要保障。下面介绍一些解题的技巧和方法。

一、由大到小

在解数学题时，范围（指定义域、值域、知识点等）越小，越便于寻找解题途径。

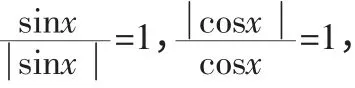
因此解得y∈｛4，0，-2｝

二、由生到熟

当我们遇到以前没有接触过的陌生题时，要设法把它转化成曾经解过的或熟悉的题目，利用已有知识、经验顺利解出原题。

例2.已知，则f（x）的最小值（ ）

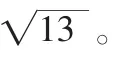
三、由特殊到一般

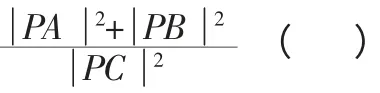
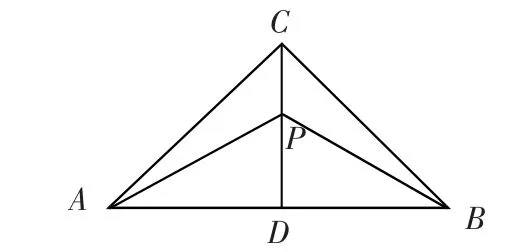
A.2 B.4 C.5 D.10

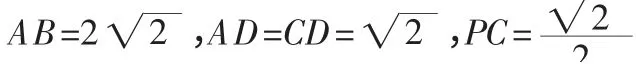
四、由反到正

当一道题从正面入手复杂繁琐，或找不到解题的依据时，要随时改变思维的方向，从结论的反面进行思考，化难为易地解出原题。

例4.从正方体的6 个面中选出3 个面，其中有2 个面不相邻的选法共有 （ ）

解：此题正面思考困难，但可这样考虑：从6 个面中任选3 个面共有C36种，但正方体的每个顶点都有3 个面相邻不符合题意，此时问题转化为C36-8=12 种。

例5.若关于x 的方程4cosx-cos2x+m-3=0 恒有实数解，则实数m 的取值范围是 （ ）

A.［-1，+∞） B.［-1，8］ C.［0，5］ D.［0，8］

解：将方程问题转化为二次函数的值域问题求解，

即方程可化为m=cos2x-4cosx+3=（cos2x-2）2-1，由cosx∈［-1，1］，得m=［0，8］，故选D。

五、由整体到部分

当按常规思路进行局部处理难以奏效或计算繁冗的题目时，要适当调整视角，把问题作为一个有机整体，从整体入手，对整体结构进行全面、深刻的分析和改造，从整体特征的研究中，找到解决问题的途径和办法。

例6.设f（x），g（x）是定义域为R 的恒大于零的可导函数，且f′（x）g（x）-f（x）g′（x）＜0，则当a＜x＜b 时有 （ ）

A.f（x）g（x）＞f（b）g（b） B.f（x）g（a）＞f（a）g（x）

C.f（x）g（b）＞f（b）g（x） D.f（x）g（x）＞f（a）g（a）

因此，在解数学题时，如果常规的思维思考受挫时，我们换一个角度思考，可能会透云见日、豁然开朗。