加强线段图教学 为解决分数应用题助力

张桂英

“画线段图”是数学问题解决中常用的一种思考策略，它能将题中蕴含的抽象的数量关系以形象、直观的方式表达出来，更清楚地反映出数量关系、结构特征，沟通学生与教师之间的思维过程的联系，帮助学生自己分析应用题中的数量关系，培养学生比较灵活的逻辑思维能力. 分数应用题是小学六年级的重要内容，是小学数学教学的重难点之一. 教师在讲解分数应用题时，应重视引导学生分析数量关系，加强单位“1”的量的判断. 分数应用题很抽象. 在教学时如何变抽象为直观，是突破教学难点的关键所在. 而画线段图是使抽象问题具体化的有效途径之一. 它对分析分数应用题中具体数量和分率之间的对应关系有着非常明显的优势. 可以说，画线段图是解决分数应用题的必不可少的途径和方法.

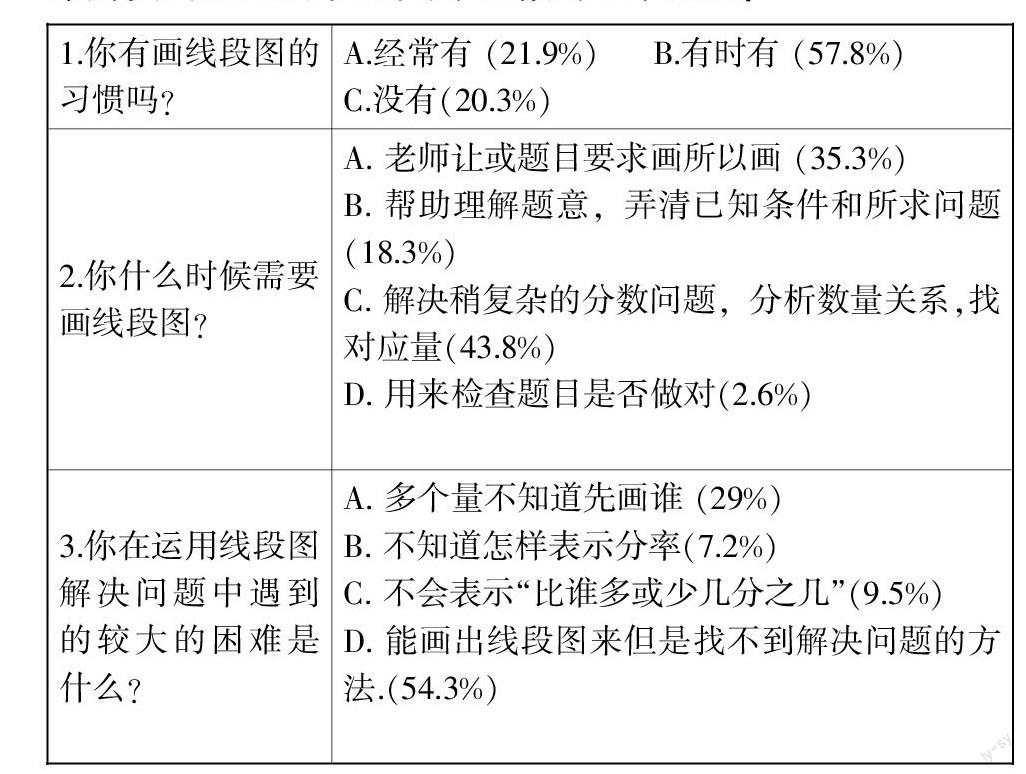
但在实际的教学中，学生却不能主动、灵活运用线段图来解决问题. 以下是我对学生做的几个调查：

通过调查问卷和实际的教学我们发现多数学生运用线段图解决分数问题时存在困难，学生无法正确画图，画得很慢、很乱、很不规范. 画线段图缺乏主动性，为了画线段图而画线段图，而不是利用线段图帮助自己解题了. 即便画出线段图也不能正确解决问题. 如何帮助学生解决这些问题，我认为要把线段图教学作为与数量关系同等重要的内容进行教学. 因为借助线段图分析问题，解决问题是解答分数应用题的一种重要的策略，特别是数量关系相对复杂的分数应用题，而学生通过画线段图帮助自己解题的能力欠缺， 因此要为学生安排有效的、较为独立的、系统的线段图学习板块，即形成“线段图”教学体系.

一、利用简单分数应用题建模，初步学会画线段图，形成技巧

学生在1-5年级的学习中，并没有经过系统的线段图训练. 一方面低年级有直观图形的辅助，即使到了五年级，由于数量关系较简单，学生未必需要借助线段图. 而画线段图并非只是一种简单的画图技巧，它需要学生多种心理活动、数学素养的参与. 因此教师应重视分数应用题的初始教学，在教学开始就注重线段图教学的建模. 教学时可借助分数的意义，让学生明确画线段图时，必须先画出单位“1”的量. 如果单位“1”的量与比较量是包含关系可以用单线. 如果单位“1”的量与比较量是并列关系一般用双线或多线. 再看单位“1”平均分的份数，如果数据较小要平均分，数据较大的可以进行“估计分”. 注意图中线段的长短要和数值的大小基本一致，比较长的线段标出大的数据而短的线段标出小的数据. 注意分清两个量是“包含关系”还是“并列关系”. 通过一定的训练，让学生掌握画图技巧.

二、利用复杂分数应用题拓展，体验画图的必要性，增强主动性

学生初步学会画线段图后，不一定能够自觉地画图帮助解题. 因此必须唤起学生的作图需要，只有让学生意识到线段图的重要作用，体会作图的意义，这种解题策略才能内化为学生的一种能力. 分数应用题本身数量关系较为抽象，解题时既要找准单位“1”的量，更要找出数量和分率的对应关系. 而复杂的分数应用题中量与率的对应关系较隐蔽，仅靠对题目的分析是无法直接找出对应关系的. 这种情况非借助线段图不可，并且要加强训练.

三、加强解图能力训练，提高分析解题能力

学生在理解题意的基础上画出线段图，但有些学生即使画出线段图，也不能正确地解答. 因为把数量关系转化成图形，再从图形抽象为数学模型，需要学生在画图的基础上进行正推和发散联想，需要不断地填补数据，才能发现解题线索. 这需要学生从形到数的再次提炼，最难的就是找到量与率的对应关系. 教学中可做如下的训练：

1. 从量找率. 例如：修一段路，第一天修了，第二天修了，还剩600米. 这条路有多长？解答这道题的关键是找出剩下的600米占全长的几分之几，可引导学生画图如右. 通过画图，可明显地看出600米的对应分率是1 - - .

2. 从率找量. 例如：修一段路，第一天修了200米，第二天修了300米，第一天比第二天少修了全长的. 求全长. 解答这道题的关键是找出这个分率对应的数量，可引导学生画图如右. 从图中可非常清楚地看出对应的数量就是（300 - 200）米.

3. 量率交错. 例如：仓库里有一批化肥，第一次取出总数的，第二次取出总数的少12袋，这时仓库里还剩24袋. 这批化肥有多少袋？这道题量率交错，如果不画图很容易出错，用（24 + 12）对应1 - - . 可引导学生画图如左. 通过画图可发现24袋里面包括12袋，应该用24袋减去12袋后才对应.

线段图的教学不是一蹶而就的事情，它需要一個反复训练的过程. 要让学生会画、愿意画、再灵活地解题. 线段图教学是学生解决分数应用题的生命线，做好线段图教学必然提高学生的解题能力并促进学生思维迈向更高的层次.