试论新课改下初中数学案例讲解活动的开展

栾小丽

【摘要】 案例课是数学课堂教学的重要类型之一，也是初中生学习技能及素养培养的有效载体. 本文作者结合新课改标准要求，简要论述了初中数学案例课教学中，教学活动的开展.

【关键词】 初中数学；案例课；讲解活动

教育学指出，数学案例是数学学科知识内容的集中概括和内在联系的生动展现，学习对象在感知探析数学案例进程中，其数学思维、探析技能等方面能够得以有效锻炼和深入发展，其培养发展功效显著. 案例课已成为数学课堂教师进行授课的重要形式之一. 案例课以数学案例为载体，以能力培养为宗旨，将教学目标和学习要求渗透融入到案例的探知解析进程之中，从而实现学习对象数学技能、数学素养提升和进步. 案例课教学，是复杂系统的工程，需要借助于先进教学理念，采用有效教学方式，开展深入互动实践活动. 本人现结合新课改标准要求，简要论述初中数学案例课教学活动的开展.

一、凸显学生主体地位，提供实践探析案例的活动空间

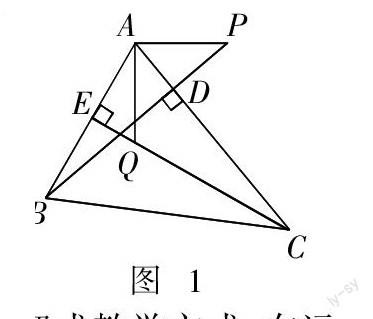
传统案例课讲解中，教师“以讲代学”，替代学生的“实践”过程，将解决问题的方法、策略“全盘托出”，直接告知给学习对象，导致所获得技能经验“肤浅”，不能“知其所以然”. 新课程改革纲要强调指出：“学生处于教学活动核心地位，应是课堂学习活动的主人，要利用其主体能动特性，组织学习对象亲身参与、亲自动手探析. ”因此，案例课讲解活动中，教师不能“越俎代庖”，全程包办，应该将初中生主体地位充分展现，鼓励和引导学生积极投身到案例条件内容、解题要求、解答思路等感知、探析活动中，围绕案例教学意图和解题目标，有针对性的设置探析案例的任务和要求，组织初中生开展自主探析、合作探究案例活动，让初中生主体特性在动手探究、思考分析的进程中充分展现. 如“如图1所示，BD，CE分别是△ABC的边AC和AB上的高，点P在BD的延线上，BP = AC，点Q在CE上，CQ = AB. 求证AP = AQ”案例讲解时，教师根据该案例的“灵活运用全等三角形的判定方法”设置意图，采用探究式教学方式，取代讲解式教学方式，在运用激励性教学语言鼓舞学生自主探究情感基础上，结合案例内容和要求，设置“案例条件中告知了哪些数量关系？”、“解题要求与条件之间存在什么联系？”、“该案例应选用什么判定方法？”等探析任务，组织初中生结合探究任务开展案例条件及要求的动手探究分析活动. 初中生自主探知问题条件意识到：“要结合问题条件与要求之间的联系，确定其判定方法的运用”，结合解题要求，合作探究推导出解析案例的基本思路为：“欲证AP = AQ，只需证对应的两个三角形全等，即证△ABP ≌ △QCA即可”. 在此过程中，教师赋予了初中生亲身探究、分析、归纳的实践活动空间，其主体特性也得到有效展示和呈现.

二、注重数学技能培养，强化探究分析案例的过程指导

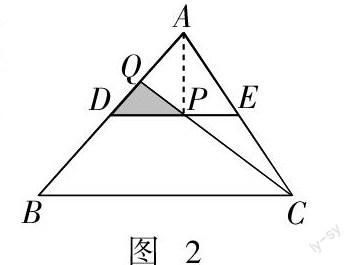
教育实践主义学者指出，学生学习实践进程，需要教师的有序引导和有效指导，学生的“学”应在教师的有序“导”中实践和前行. 众所周知，初中生由于自身数学学习素养与数学学科学习目标要求之间的差距，决定了初中生的数学学习实践活动需要教师的科学指导和细心讲解. 这就要求，初中数学教师案例讲解时，要将数学学习能力培养放在首位，在尊重学生主体特性，提供实践活动的同时，切实发挥好教师的主导指导作用，对初中生案例探究过程、解析思路以及解答过程等活动表现及不足，进行有的放矢、针锋相对的点拨和指正，进一步帮助初中生明晰案例内容，理清内在联系，掌握解析策略，促进解题技能提升，掌握正确解题策略. 如在“已知，如图，DE是△ABC的中位线，P是DE的中点，试求出S△DPQ ∶ S△ABC =的值”案例思路的推导过程中，初中生通过分析条件、找寻关系等活动，指出该问题解答的基本思路应该是：“连接PA，由相似三角形的判定定理、三角形中位线定理等内容，得到S△ADE ∶ S△ABC = 1 ∶ 4，S△DPQ ∶ S△APQ = 1 ∶ 2，通过等量替换，得到S△DPQ ∶ S△ABC = 1 ∶ 24”. 此时，教师针对初中生所开展的思考分析活动，所得到的解题思路内容，进行讲解指导活动，指出： “在此案例解析中，需要正确利用相似三角形的判定和性质，三角形中位线定理等内容”. 初中生借助于教师的指导，意识到在探析活动中需要注意的关键点，从而进行针对性的整改，形成良好学习习惯，提升数学学习技能.

三、坚持教学双边结合，搭建互动评析案例的交流时机

教学活动的过程，不是教与学之间相互孤立、互不交集的独立活动，而是教与学之间相互沟通、深入交流的互动活动. 教师的“教”与学生的“学”之间，应该相互交错，深入互动. 案例课讲解活动中，教师需要与学生群体之间进行深入、细致的交流、研讨活动，以此及时了解掌握学生群体在案例探知分析活動进程的实际情况，围绕突出问题或重点难题，引导学生进行深入细致的交流、讨论活动，让学生能够获得展示解题观点的阐述时机，展示解析问题案例的见解路数，教师针对学生案例解答思路内容，进行讲解指导，帮助学生形成正确解析思路和方法，使学生形成更加科学、合理的思维过程，树立良好解题技能. 如“一次函数的图像”巩固练习教学反馈环节，教师摒弃传统的“教师评讲”的单一模式，采用“师生互动”的评讲活动，组织学生结合探析解答案例所得，开展评析案例的阐述活动，并有意识的让学生代表运用数学语言进行呈现. 教师根据学生阐述内容，与学生进行交流，引导学生自我剖析，开展进一步的反思整改活动，教师此时强调指出：“解答此类问题，需要正确理解掌握一次函数图像的特征”. 初中生深切认识到该问题解答的关键之处在于：“正确理解一次函数图像的特征”，需要理清“一次函数图像”与一元一次不等式、正比例函数等图像之间的内在联系.

总之，初中数学教师在讲解案例进程中，要切实把准新课改内涵要义，紧盯学生主体特性，紧扣能力培养要义，将教师的“教”与学生的“学”之间进行科学调控，有效衔接，实现初中生对案例解析策略的有效掌握，数学技能的有效提升.