间接解析粗对准过程中的抗线干扰方法*

单斌，秦永元，张金亮，王新国，周小刚

(1西北工业大学自动化学院，西安 710072;2第二炮兵工程大学控制工程系，西安 710025)

间接解析粗对准过程中的抗线干扰方法*

单斌1，2，秦永元1，张金亮1，王新国2，周小刚2

(1西北工业大学自动化学院，西安 710072;2第二炮兵工程大学控制工程系，西安 710025)

为提高捷联惯导间接解析粗对准抗线干扰能力，分析了常用频域数字预滤波算法对线干扰的改善效果和局限性。在此基础上，设计了一种基于时域内多项式回归思想的无时延抗线干扰算法，并同频域数字预滤波算法仿真比较，验证了算法有效性。仿真结果表明：该算法可有效抵抗对准过程中的不同类型线干扰影响，对突变型线干扰的效果更优，算法简单，无时延，可在较短时间内满足进入精对准过程的精度要求。

捷联惯导;间接解析粗对准;线干扰;数字预滤波;多项式回归

0 引言

捷联惯导初始对准的精度和时间是影响系统导航精度和快速反应能力的关键指标［1-2］。其过程经由解析式粗对准和卡尔曼滤波精对准过程实现，利用惯导系统线性化的小失准角误差方程构造滤波器，要求姿态误差φ满足小角度条件［3］。实际对准过程中惯导基座通常处于复杂干扰环境，包括风扰、海浪、人员走动等，这些因素通过污染陀螺仪和加速度计量测，使对准收敛时间延长，同时降低对准的精度［4］。精对准阶段可通过姿态更新过程和滤波器参数调节约束干扰因素的影响，因此上述干扰主要作用在粗对准阶段，造成解析式粗对准在很长时间内不能满足精对准要求的小角度条件［5］。

干扰因素按其表现形式可分为角干扰和线干扰两种类型。角干扰表现为惯导系统相对自身原点的晃动，使得陀螺仪不能有效量测ωie。线干扰表现为惯导系统相对原点的振动，使得加速度计对g的量测存在误差。传统的静基座直接解析粗对准算法以惯导系统对ωie和g的量测构造矢量，利用矢量在载体系b和导航系n的投影转换关系求解姿态矩阵Cnb，完成粗对准。在角干扰环境下干扰角速度远大于地球自转角速度，传统静基座解析式粗对准算法失效，此时可用参考信息只有g。为解决晃动基座下的粗对准问题，秦永元［6］教授提出利用重力加速度g在惯性空间不同时刻投影构造矢量进行粗对准的思路，并进一步设计了基于惯性系下重力加速度积分的间接解析粗对准算法。该算法将角干扰视为有效机动，利用姿态更新过程实现对角干扰的隔离处理。练军想［7］、白亮［8］、杨鹏翔［9］等对上述算法进一步分析，发现线干扰成为影响对准精度和对准时间的主要因素，并分别设计了FIR和IIR数字预滤波算法对间接解析式粗对准算法进行了改善处理。基于上述研究，文中对FIR和IIR的滤波效果进行了分析，指出了频域数字滤波的局限性，并在此基础上利用重力加速度积分信号的时域特性设计了基于时域内信号拟合处理的抗线干扰算法，仿真验证了算法的抗线干扰效果，与FIR和IIR比较，实现了更强的抗干扰能力。

1 SINS间接解析粗对准算法

文中用到的坐标系定义如下：

1)导航坐标系(n)：采用东-北-天地理坐标系。

2)载体坐标系(b)：原点位于惯性组建中心，oxb、oyb、ozb轴分别沿载体横轴向右、纵轴向前、立轴向上的方向。

3)初始惯性坐标系(i0)：初始对准起始时刻，地球坐标系e相对惯性空间凝固所得惯性坐标系。

4)载体惯性坐标系(b0)：初始对准起始时刻，b系相对惯性空间凝固所得惯性坐标系。

载体在t时刻的姿态矩阵可以通过下式获得：

考虑到很小量级的速度干扰也会对上述算法对准精度和时间产生较大影响。因此，线干扰基座下采用间接解析对准须设计相应抗干扰算法，否则粗对准不能在期望时间内达到精对准的小角度条件。

2 频域内数字滤波预处理算法

图1 重力加速度在惯性系下旋转示意图

在惯性系i0下观察g可知，沿x轴和y轴为低频变化信号的组合，变化频率为地球自转频率(1.16× 10－5Hz)，沿z轴为常值分量，如式(4)所示。同样，将加速度计量测投影到惯性系b0系，如式(5)所示，式中fd为重力加速度之外的干扰加速度。

由于b0系同为惯性系，因此gb0具有与gi0相同的频率组成。对准过程中，gb0作为加速度计量测fb0中的有效成分，远小于线干扰信号的频率(大于0.05 Hz)。基于上述分析可知，通过设置低通数字滤波器对fb0进行数字滤波，理论上可以滤除绝大多数的线干扰成分，进而提高fb0中gb0分量的信噪比，从而提高粗对准算法的对准精度，并缩短对准时间。对式(4)积分或将式(2)展开得到：

同理vb0(t)的有用成分具有与vi0(t)相同的频率组成。与式(4)比较可知，积分过程使得信号中增加了斜坡分量t，考虑斜坡信号的频率集中在0附近的很小频率范围内，因此同样可利用数字低通滤波器对(t)进行滤波处理，滤除高频干扰信号的影响。

工程上常用的数字滤波器包括有限冲击响应滤波器FIR和无限冲击响应滤波器IIR两种。滤波后，由vb0(t)得到的(t)在时间轴上落后于vi0(t)，发生了时间延迟，故必须对vi0(t)进行相应时延处理，使其与(t)匹配。针对文中初始对准问题，采用FIR对(t)进行滤波后，利用计算的时间延迟参数对vi0(t)进行时间补偿，可实现抗线干扰的目的。与此相比，由于IIR滤波无确定时延参数，为实现滤波后的时间匹配问题，就必须对vb0(t)和vi0(t)进行相同的滤波处理，这是利用了二者频率构成相同的特性。综上所述，加入FIR和IIR滤波预处理的间接解析粗对准算法流程分别如图2和图3所示。

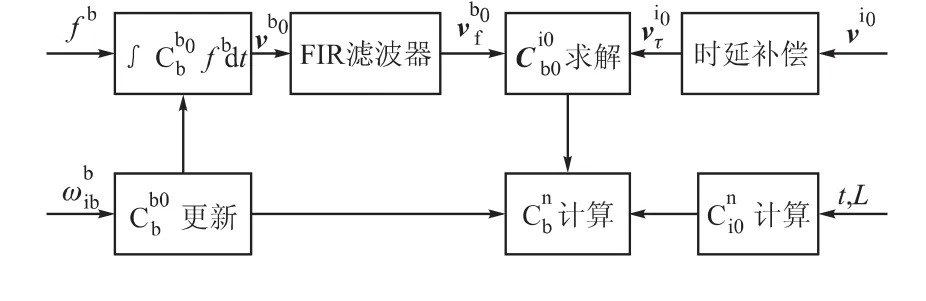
图2 FIR预滤波间接解析对准算法

图3 IIR预滤波间接解析对准算法

由于数字滤波是在频域内对干扰信号进行处理，因此不可避免会存在以下几个问题：1)考虑惯导系统采样频率较高(一般为200 Hz)，干扰信号频率较低(大于0.05 Hz)，有用信号频率更低(1.16×10－5Hz)，因此设计FIR低通滤波器的阶次通常较高，将达到数千阶甚至上万阶，由此导致FIR滤波的延迟时间达到数十秒。2)对IIR滤波器，由于其为零极系统，系数精度受字长限制存在量化误差，该量化误差与乘法器的舍入误差一起对滤波输出会有积累效应，以致输出误差放大，实际应用中只能采用简单一二阶系统构成的级联或并联形式。3)数字滤波处理突变干扰的能力较差，因此当惯导基座线干扰突然变化时会出现对准精度下降的问题。上述问题作为频域数字滤波原理上的固有问题，难以改善，特别当线干扰情况复杂时，利用频域数字滤波不能实现理想的抗干扰效果。为解决这一问题，需考虑频域滤波之外的处理方法。

3 时域内数字拟合预处理算法

对干扰信号进行预处理，除上述频域内数字滤波算法之外，还可以利用信号的时域特性设计相应的处理算法，包括曲线拟合、多项式回归、数据平滑等方式。这些方式要求信号必须在时域内存在确定的变化趋势，在此基础上利用参数辨识算法确定出信号的时域模型，实现消除干扰的目的。分析式(6)可知，重力加速度在惯性系下的积分具有确定的表达形式，

可知，此时对线干扰条件下的vb0(t)数据做基于多项式模型的多项式回归处理，利用加权最小二乘方法拟合得到Bx1～Bz39个参数后，即可实现的求解。考虑到实际模型中t2和t3系数量极很小，受干扰影响辨识的相对精度较低，直接利用Bx1～Bz3求解稳定性差。为此，可利用辨识出的回归模型重新计算vb0(t)，利用得到的(t)进行间接解析粗对准，可获得更好的对准结果。

基于上述分析，得到基于多项式回归处理的抗线干扰解析对准算法流程如图4所示。

图4 多项式拟合间接解析对准算法

比较图4与图2、图3可知，由于数据拟合算法是在时域内对数据进行实时处理，拟合过程中不引入时间延迟，因此不需对vi0(t)数据做时延处理。同时由于拟合算法采用最小二乘优化准则，对数据中的突变干扰具有更强的抵抗效果。为解决上述多项式回归算法的实时性问题，计算时采用递推最小二乘算法，

4 仿真分析

设仿真基座所处纬度为30°，载体基座的晃动频率和范围设置为：俯仰角θ(0.5 Hz，－5°～5°)，横滚角γ(0.4 Hz，－10°～10°)，方位角ψ(0.3 Hz，－20°～20°)。

惯导系统的陀螺和加计参数设置为：陀螺常值零偏0.01°/h，角随机游走0.001°/。加计偏置100 μg，加计速度随机游走10 μg/。陀螺和加计刻度系数误差为100×10－6。采样频率200 Hz。

仿真设置FIR和IIR滤波器分别为：FIR选用切比雪夫最佳一致FIR滤波器，通带截止频率设置为0.1 Hz，阻带下限截止频率设置为0.5 Hz，通带衰减设置为3 dB，阻带衰减设置为40 dB。IIR选用巴特沃思IIR滤波器，频率设置与FIR相同。

为仿真验证FIR、IIR和多项式回归算法抗线干扰能力的不同，仿真设置以下几种线干扰条件：

1)线干扰类型设置为白噪声，满足均值为0，标准差为0.01 m/s。

2)高频线干扰，干扰频率为1 Hz，干扰幅值为0.05 m。

3)低频线干扰，干扰频率为0.2 Hz，干扰幅值为0.05 m。

4)突变线干扰，在30～31 s，80～81 s，120～131 s，210～211 s四个时间段内设置突变类型的线干扰，设为0.01 m/s。

在上述仿真条件设置下，分别利用FIR、IIR和多项式拟合对数据预处理后进行间接解析粗对准，四种干扰条件下的对准误差如图5～图8所示。受篇幅限制，图中只给出方位失准角φU的估计误差作为比较标准，这也与实际情况中以方位精度衡量对准性能的做法相一致。

图5 白噪声干扰条件下粗对准误差

图6 高频线干扰条件下粗对准误差

图7 低频线干扰条件下粗对准误差

图8 突变干扰条件下的粗对准结果

从图5看出，白噪声干扰条件下，采用FIR、IIR和回归预处理都可有效抵抗线干扰影响，在100 s时间内达到精对准的小角度要求。从图6看出，高频线干扰条件下，IIR抗线干扰能力最强，FIR和回归预处理方法也能有效实现抗干扰的目的。从图7中看出，低频线干扰条件下，由于干扰频率介于通带和阻带过渡段，导致FIR和IIR数字滤波算法的效果不佳，而回归预处理算法受干扰频率的影响较小，仍能在较短时间内达到小角度条件。从图8看出，当存在突变型线干扰(如由波浪运动引起的舰船摆动)时，数字滤波算法由于其自身频带限制不能完全滤除干扰的影响，到导致对准过程中存在跳动误差，而回归预处理由于是曲线拟合算法的一种实现手段，对突变型故障有原理上的平滑作用，因此对准结果的平滑性更好。综合上述分析可知，文中基于多项式回归的抗线干扰初始对准算法，处理各种不同类型线干扰的综合能力最优，尤其在存在突变型线干扰的情况下，更适合于工程应用。

5 结论

文中以基于惯性系下重力加速度积分的间接解析粗对准算法为研究对象，对其抗线干扰性能进行了理论和仿真分析。在此基础上设计了针对线干扰的FIR和IIR频域数字预滤波算法，以及基于多项式回归思想的时域曲线拟合算法，并以多种类型线干扰为仿真条件，对上述三种抗线干扰算法的性能进行了仿真分析。结果表明，频域预滤波算法处理高频线干扰的能力最优，处理低频线干扰的能力受其频带特性的制约。此外，在突变型线干扰条件下，对准结果存在跳变误差。而时域回归算法干扰频率的影响较小，处理突变型干扰的能力最强，更适用于线干扰复杂的对准环境。

［1］Titterton D H，Weston J L.Strapdown inertial navigation technology［M］.2nd ed.Reston，VA：American Institute of Aeronautics and Astronautics，2004.

［2］Grewal M S，Weill L R，Andrews A P.Global positioning systems，inertial navigation，and integration［M］.2nd ed.Hoboken，N J：Wiley-Interscience，2007.

［3］秦永元.惯性导航［M］.北京：科学出版社，2006.

［4］Gu Dongqing，El-Sheimy N，Hassan T.Coarse alignment for marine SINS using gravity in the inertial frame as a reference［C］∥IEEE Position，Location and Navigation Symposium 2008.Monterey，CA：IEEE/ION，2008：961-965.

［5］Britting，Kenneth R.Inertial navigation system analysis［M］.Norwood，USA：Artech House Publishers，2010.

［6］秦永元，严恭敏，顾冬晴，等.摇摆基座上基于信息的捷联惯导粗对准研究［J］.西北工业大学学报，2005，23(5)：681-684.

［7］LIAN Jun-xiang，HU De-wen，WU Yuan-xin，et al.Resarch on SINS alignment algorithm on FIR filters［J］.Journal of Beijing Institute of Technology，2007，16(4)： 437-442.

［8］白亮.弹载及车载捷联惯导对准技术研究［D］.西安：西北工业大学，2010.

［9］杨鹏翔.捷联惯性基车载组合导航系统关键技术研究［D］.西安：西北工业大学，2010.

Anti-vibration Method in Indirect Analytic Alignment

SHAN Bin1，2，QIN Yongyuan1，ZHANG Jinliang1，WANG Xinguo2，ZHOU Xiaogang2
(1School of Automation，Northwestern Polytechnical University，Xi’an 710072，China; 2Department of Control Engineering，The Second Artillery Engineering University，Xi’an 710025，China)

In order to improve anti-vibration abilities of an indirect analytic alignment algorithm for SINS，common frequency-domain digital filtering methods was analyzed to estimate anti-vibration abilities as well as their limitations.On the basis，an anti-vibration algorithm without time delay was proposed based on polynomial regression in time-domain，and simulations were conducted to validate its effectiveness compared with the frequency-domain digital filtering methods.The result shows that the polynomial regression method can effectively handle different kinds of vibrations，sudden change of vibration with simple algorithm and no time delay.The anti-vibration algorithm can meet the requirement of fine alignment in short time.

SINS;indirect analytic alignment;linear vibration;digital filtering;polynomial regression

V249.3

A

10.15892/j.cnki.djzdxb.2015.05.020

2014-09-23

总装备部惯性预研基金资助

单斌(1974－)，男，安徽无为人，副教授，博士研究生，研究方向：惯性导航及测试技术研究。