一种自适应的粒子局部PHD滤波*

童骞，李鸿艳，危璋，毛少锋，鹿传国

(1空军工程大学信息与导航学院，西安 710077;295806部队，北京 100000)

一种自适应的粒子局部PHD滤波*

童骞1，李鸿艳1，危璋1，毛少锋1，鹿传国2

(1空军工程大学信息与导航学院，西安 710077;295806部队，北京 100000)

针对SMC-PHD滤波算法精度不高、计算量大的问题，提出一种自适应的粒子局部概率假设密度滤波算法。该算法首先利用加速度协方差自适应调整波门大小，划分目标区域与杂波区域，然后在各自区域分别进行粒子概率假设密度滤波，以达到提高滤波性能，减少计算量的目的。仿真结果表明，与SMC-PHD算法相比较，本算法提高滤波精度并减少了计算量。

粒子PHD;局部PHD;自适应

0 引言

针对以数据关联为基础的传统多目标跟踪理论存在“组合爆炸”、NP-Hard［1-2］等问题，R.Mahler［2-3］采用随机有限集(RFS)来表示多目标的状态和量测集合，建立了基于随机集(RFS)的多目标运动模型，提出计算上可实现的概率假设密度［3］(probability hypothesis density，PHD)滤波的概念，绕过了数据关联。

目前，PHD滤波实现主要有两种方法：一是用闭合的解析形式近似PHD分布，即高斯混合PHD(GMPHD)［4-5］;二是用一组带权值的随机粒子逼近PHD分布，即粒子PHD(SMC-PHD)［6-7］。前者适用于高斯线性模型，而后者无高斯线性约束，适用范围更广。然而无论是GM-PHD或是SMC-PHD，在进行权值更新的时候，都需计算每一个高斯分量或每一个粒子对于所有量测的似然度［8］，这样的做法不仅效率低下且无必要。

文献［9］提出了一种基于Ad-hoc网络对整个量测区域进行划分，然后在每个区域单独进行GMCPHD的方法，但这种方法必须保证划分区域没有重叠，因此不适用于目标交叉的情况。参考以上文献，文中提出一种利用自适应跟踪波门进行区域划分，然后在各个区域分别使用SMC-PHD的局部PHD滤波算法。

1 粒子PHD滤波

1.1 运动模型建立

设目标运动模型为：

其中：xk∈Rm和zk∈Rm分别为状态向量和量测向量;f(·)和h(·)分别表示状态转移函数和量测方程;wk－1、vk分别为系统过程噪声和量测噪声，服从均值为零;方差分别为Qk－1、Rk的高斯分布。

1.2 PHD滤波描述

PHD滤波其本质是基于随机集(RSF)理论在Bayes框架下的一种扩展应用，其主要的区别在于PHD滤波是在递推运算概率假设密度，而Bayes滤波在递推运算后验概论密度。

式中：D(·)表示目标强度，其在状态域上的积分为目标的个数;γk(xk)是新生目标强度;βk|k－1(xk|xk－1)是源自xk－1的衍生目标强度;fk|k－1(.|.)是单目标状态转移密度函数;ek|k－1(xk－1)是目标存活概率;φk，z(xk)=PD(xk)gk|k(z|xk)，gk|k(z|xk)为单目标似然函数.PD(xk)为目标被检测概率;Dk(z)=κk(z)+Ck(z)为量测z的强度，κk(z)是杂波强度，Ck(z)=∫φk，z(xk)Dk|k－1(xk|Z1：k－1)dx。

1.3 SMC-PHD滤波实现

PHD滤波更新方程式(3)等效为权值更新方程：

对于量测集中的每个量测z∈Zk，有：

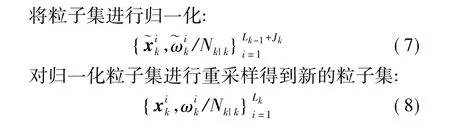
2 自适应粒子局域PHD滤波

2.1 自适应粒子局域PHD滤波描述

针对SMC-PHD量测中存在的大量杂波影响着目标状态估计精度，计算量大的问题，考虑到大量杂波量测对于真实目标权值更新无太大影响，以及某个目标产生的真实量测对于其它非相邻目标权值更新影响很小的实际情况，因此可以先利用一步预测结合自适应波门划分目标存在区域和杂波区域，然后利用目标存在区域的量测分区进行SMC-PHD，忽略杂波区域的量测，另外考虑到新生目标的情况，单独运行一个SMC-PHD，利用所有量测对此进行更新。通过这些方法提高精度，同时减少了计算量。

2.2 自适应波门选择

粒子局部PHD滤波与SMC-PHD滤波最重要的区别在于前者首先进行了区域划分，通过区域划分能有效减少在复杂杂波下的计算量，同时提高精度，因此区域的划分影响滤波结果，文中利用一个自适应跟踪波门对区域进行划分提高滤波效果。

文中考虑到目标机动情况引入一种自适应跟踪波门，若量测z(k)满足：

式中：Sk|k－1(j)为第j个波门新息协方差;σ为加速度协方差;T为量测获取时间间隔;γ为根据实际情况选择的参量。

波门的体积公式为：

通过在波门判定式中引入加速度协方差σ，从而使得波门能在目标匀速运动中自适应的减小波门，排除更多杂波;在目标机动过程中自适应的扩大波门防止目标丢失，增强算法的稳定性。

2.3 自适应粒子局部PHD滤波流程

1)粒子分类并添加标签。设在k－1时刻，目标个数为Nk－1，通过聚类的方法提取目标的状态并将粒子群分为Nk－1类，同时为每一类粒子添加标签j=1，…，Nk－1。

2)划分区域。以Nk－1个目标状态的一步预测为中心，通过式(9)判定各个量测与各个目标的从属关系，类似于航迹起始的操作，从而为每一个目标划分目标存在区域与杂波区域。

3)权值更新。在每一个目标存在区域内，使用区域内的量测对该区域的目标权值进行更新。

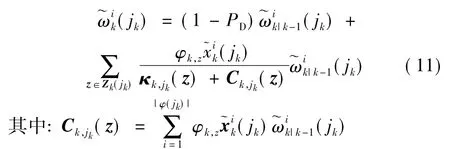
4)新生目标更新。根据式(5)使用所有量测更新新生目标粒子，并将新生粒子标记为)j。

6)重复2)～4)步骤。

3 仿真分析

为了验证算法的有效性，通过两组对比实验，对文中所提算法与粒子局域PHD算法以及粒子PHD算法的性能进行对比分析。

3.1 实验一仿真环境介绍

设初始时刻存在两个目标，初始状态分别为［100，100，3 000，－100］和［100，100，2 000，100］，第三个目标出现时刻为第20 s，初始状态为：［150，100，3 500，0］。每个扫描周期内的杂波服从均值为5的泊松分布，均匀分布在整个观测区域。目标存活概率为1，检验概率为0.95。观测站位于(0，0)，直角坐标系下观测区域为［0，500］·［0，3 000］。过程噪声w(k)为高斯白噪声，方差为5(m/s)2，v(k)为量测噪声，方位角误差方差为0.005 rad2，距离误差方差为200 m2。蒙特卡罗仿真50次，跟踪时间为50 s，每个目标分配的粒子个数为1 000。多目标跟踪性能的评价标准采用最优子模型分配(optimal subpattern assignment，OSPA)距离。

目标跟踪模型如下：

3.2 实验一仿真结果与分析

从图1可以看出在目标数目估计准确度上，三种算法都能准确估计目标数目。从图2以及表1可以看出，在目标匀速运动时，基本粒子PHD算法OSPA距离较大，文中提出的算法与粒子局域PHD算法OSPA距离相对较小，且比较稳定，同时两者所耗时间相当。粒子局部PHD算法之所以能在减少运算时间的同时提高跟踪精度，主要在于通过划分区域，排除一些杂波，提高了跟踪精确度，并减少运算时间。

图1 目标个数估计

图2 OSPA距离图

表1 各算法性能对比表

3.3 实验二仿真环境介绍

实验初始条件不变，目标运动由匀速运动变为以ω=0.05 rad/s做圆周运动。蒙特卡罗仿真50次，跟踪时间为50 s，每个目标分配的粒子个数为1 000。多目标跟踪性能的评价标准采用最优子模型分配(optimal subpattern assignment，OSPA)距离。

3.4 实验二仿真结果与分析

从仿真曲线图3中可以看出在目标估计准确度上，文中提出的算法与粒子局域PHD算法都能有效估计目标数目，而基本粒子PHD则有一定误差。从图4以及表2中可以看出，目标进行非匀速运动时，文中提出的算法与粒子局域PHD算法OSPA距离相对较小，文中提出的算法虽然时间稍多，但精度比局部PHD更高。主要由于文中算法考虑到目标机动，将划分门限改为自适应门限，提高了目标机动时的精确度，与此同时时间增加少许。

图3 目标个数估计

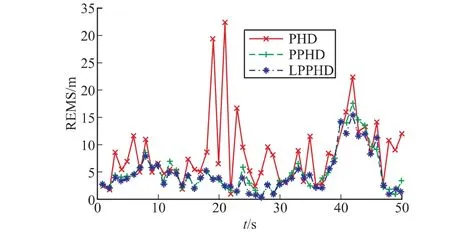
图4 OSPA距离图

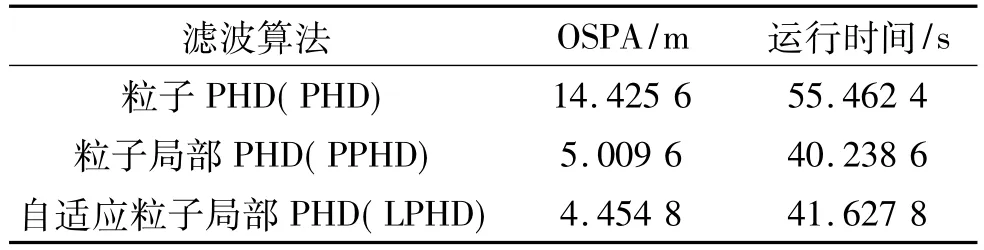
表2 各算法性能对比表

4 结论

文中针对粒子PHD算法实际运用存在精度不高、计算量过大的问题，引入局部滤波的思想，同时考虑到目标机动的情况，提出一种自适应粒子局域PHD滤波算法。利用自适应波门划分区域，滤除部分杂波，从而减少实现PHD滤波计算量，同时提高精度。仿真实验表明，文中的工作改善了粒子PHD的性能，不仅提高了跟踪精度，同时也减少了计算量。

需指出的一点是，文中仅是考虑到杂波服从均匀分布，如何将所提算法运用到杂波聚集出现等更加复杂的实际情况中，将是下一步研究的重要方向。

［1］Bar-Shalom，Li X R.Multitarget-multisensortracking：Principles and techniques［M］.Storrs，CT：YBS，1995.

［2］Mahler R.Statistical multisource multitarget information fusion［M］.Boston：Artech House，2007.

［3］David LHall，James Llinas.Handbook of multisensor data fusion［M］.2nd ed.New York：CRC Press，2008.

［4］Vo B N，Pasha A，Tuan H.A Gaussian mixture PHD filter for nonlinear jump Markov models［C］∥Proceedings of the 45th IEEE Conference on Decision＆Control.San Diego，CA，USA，2006：3162-3167.

［5］Vihola M.Rao-blackwellised particle filtering in random set multitarget tracking［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，43(2)：689-705.

［6］Vo B N，Singh S，Doucet A.Sequential Monte Carlo methods for Bayesian multi-target filtering with random finite sets［J］.IEEETransactions on.Aerospace and Electronic Systems，2005，41(4)：1224-1245.

［7］Erdinc O，Willett P，Bar-Shalom Y.Probability hypothesis density filters for multitarget multisensor tracking［C］∥8th International Conference on Information Fusion，Philadelphia，PA，USA，2005.

［8］王晓，韩崇昭.用于机动目标跟踪的多模型高斯混合概率假设密度滤波器［J］.控制与决策，2012，27(12)： 1864-1869.

［9］连峰，韩崇昭，刘伟峰，等.高斯混合扩展目标概率假设密度滤波器的收敛性分析［J］.自动化学报，2012，38(8)：1343-1352.

［10］龙建乾，杨威，付耀文.基于改进的PHD粒子滤波的多目标跟踪技术［J］.信号处理，2011，27(9)： 1296-1300.

［11］赵欣，姬红兵，杨柏胜.基于随机集的RBPF多目标关联跟踪算法［J］.电子学报，2011，39(3)：505-510.

［12］胡士强，敬中良.粒子滤波算法综述［J］.控制与决策，2005，20(4)：361-365.

［13］ZHAN Ronghui，WAN Jianwei.Iterated unscented Kalman filter for passive target tracking［J］.IEEE Transactions on Aerosp-ace and Electronic Systems，2007，43 (3)：1155-1163.

［14］孙枫，唐李军.Cubature粒子滤波［J］.系统工程与电子技术，2011，31(11)：2554-2557.

［15］Arasaratnam I，Haykin，S，Elliott，R J.Discrete-time nonlinear filtering algorithms using Gauss-Hermite quadrature［J］.Proceedings of the IEEE，2007，95(5)： 953-977.

An Adaptive Particle Local PHD Filter

TONG Qian1，LI HongYan1，WEI Zhang1，MAO Shaofeng1，Lu Chuanguo2
(1Information and Navigation College，Air Force Engineering University，Xi’an 710077，China; 2No.95806 Unit，Beijing 100000，China)

Filter with standard particle probability assumption is of less accuracy and larger computation complexity.To solve the problem，an adaptive particle local PHD filter algorithm was proposed.The approach makes use of accelerate covariance to adjust adaptive gate，the size of which changes according to target movement condition.The object region and clutter region are separated，part of clutter eliminated，and particle PHD filter is performed in each region separately，with simulation at last.The simulation reveals that compared with standard PHD filter，the amount of calculation is reduced while the precision increases.

particle PHD;local PHD;adaptive

TN953

A

10.15892/j.cnki.djzdxb.2015.05.007

2014-10-21

童骞(1991－)，男，湖南娄底人，硕士研究生，研究方向：目标跟踪。