基于无迹变换的多目标高斯混合粒子PHD滤波*

刘欣，冯新喜，孔云波，王兢

(1空军工程大学信息与导航学院，西安 710077;294969部队，上海 200400)

基于无迹变换的多目标高斯混合粒子PHD滤波*

刘欣1，冯新喜1，孔云波1，王兢2

(1空军工程大学信息与导航学院，西安 710077;294969部队，上海 200400)

针对在杂波环境下，一般的高斯混合粒子PHD出现滤波精度不高、滤波发散的问题，提出了一种基于无迹变换的高斯混合粒子PHD。该算法在高斯混合粒子PHD预测的基础之上，采用无迹变换进行重要性采样，结合观测值对采样粒子进行更新，获得重要性密度函数，然后对PHD进行更新。最后，将该算法与高斯混合粒子PHD进行比较;仿真结果表明，该算法在有效提高高斯混合粒子PHD精度的同时，还能提高系统的稳定性。

多目标跟踪;概率假设密度滤波;无迹变换;高斯混合粒子PHD

0 引言

在多目标跟踪问题中，由于各目标的状态、目标的数目以及杂波的产生等都是随着时间的变化而变化的，传统的方法一般都是运用关联算法，将传感器与目标对应起来，例如最近邻算法、PDA、JPDA算法以及多假设跟踪算法等，但是这些算法中会存在计算量过大、关联不精确等问题，这一直是学术界和工程应用领域的一个热点问题。

1997年Mahler首次系统地在随机集理论框架下将多传感器多目标的跟踪问题描述为贝叶斯估计问题，并给出了相应的递推公式，开辟了基于随机集理论目标跟踪问题［1］。为降低算法的复杂度，Mahler通过一些智能的方法得到了概率假设密度滤波器［2］以及势概率假设密度滤波器［3］。与传统的关联算法相比较，基于随机集的多目标跟踪算法不仅避免了复杂的数据关联过程，而且大大的提高了跟踪的速度与精度。

目前，PHD算法有两种实现方式［4］：一种是高斯混合PHD［5］，另外一种是粒子PHD［6］。前一种是在噪声模型是高斯模型下建立的，对模型的依赖比较严重，计算量相对较小［7］，但常常会出现计算精度不高等问题;后者虽不受噪声模型的限制，且滤波精度相对较高，但是在滤波中计算量相对较大，常常出现滤波发散的情况，并且重要性概率密度函数往往没有考虑观测数据，往往使得跟踪的效果不能达到满意的效果。

针对以上的问题，文献［8］提出一种高斯混合粒子PHD(简称为GMP-PHD)的方法，这种方法充分结合了GM-PHD和SMC-PHD的优点，通过粒子的方式将目标的PHD近似为混合高斯形式进行PHD滤波，在预测与更新时进行粒子近似和重采样，能在一定程度上提高了算法的精度;但是在采样过程中，其重要性密度函数没有涉及量测信息，在实际情况中往往会与真实值有一定的偏差，对于感知需求较高的系统来说，该算法却不一定能达到预期的效果。

针对GMP-PHD所存在的问题，提出一种基于无迹变换的高斯混合粒子PHD算法(简称为U-GMPPHD)。该算法在原始滤波的基础之上，采用无迹卡尔曼滤波［9，12］进行重要性采样，结合观测值对粒子进行更新，获得重要性概率密度函数［10］，这种方法在原有的基础之上，大大提高了滤波的精度，并且系统的稳定性也有了明显增强。

1 PHD滤波基础

1.1 PHD滤波

PHD滤波与传统的卡尔曼滤波有着相似的步骤，也分为预测与更新［8］两步。

1)预测

式中：γk(xk)表示新生目标的PHD;bk|k－1(xk|xk－1)表示衍生目标的强度;ek－1(xk－1)fk|k－1(xk|xk－1)表示存活目标的强度;ek－1(xk－1)是目标的存活的概率; fk|k－1(xk|xk－1)是单个目标的状态转移概率，在高斯混合情况下表示为：fk|k－1(xk|xk－1)=N(x;Fkxk－1，Qk－1)。

2)更新

更新方程包含漏检的部分和检测更新部分，表示如下：

式中：pd是目标的检测概率;g(z|x)表示目标的似然函数;κk(z)表示杂波的强度。

1.2 GMP-PHD滤波

在高斯混合框架下的PHD滤波是将PHD的形式表示为多个高斯项相加的形式，仍然分为预测与更新两步，由于衍生部分一般占总PHD很小比例的一部分，因此在这里将衍生部分忽略不计。

2)更新

在高斯混合情况下，似然函数可以表示为gk(z| x)=N(z;hk(x)，Rk)，更新方程表示如下：

根据重要性采样定理，检测更新部分可以进行简化，简化后的更新方程如下：

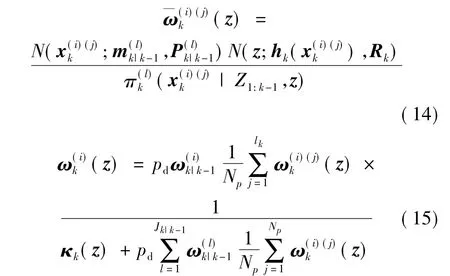
这种算法克服了单一的高斯混合和粒子PHD算法的缺陷，在计算精度上有了很明显的提高，但是对于要求更高的系统来说，这样的算法不一定能达到预期的效果，为此，提出了一种改进的高斯混合粒子PHD算法。

2 U-GMPPHD算法流程

2.1 初始化

根据先验概率分布P(xk－1)进行采样，可以得到N个粒子，并且粒子的数目与目标的数目成比例;若假设初始的目标数为N0，则每个目标用Np个粒子来表示，那么N=N0Np。采样粒子可以表示为根据初始化中得到的粒子，可以得到如下的信息：

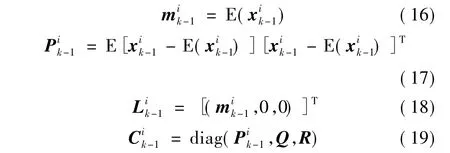
其中Q、R分别是过程噪声与量测噪声的自协方差。并且假设k－1时刻，目标的概率假设函数是高斯混合形式，可表示为：

2.2 利用无迹变换进行重要性采样

由初始化中所得到的参量可以对每个粒子进行重要性采样，利用无迹变换的原理进行采样，可以得到(2n+1)个sigma采样点：

2.3 粒子的预测与更新［10］

在重要性采样之后，可以根据采样点的状态与权值对粒子进行预测，然后利用新获得的量测对预测进行更新，具体的步骤如下：

2.4 采样

通过上述的预测与更新可以得到粒子的均值与方差，假设重要性概率密度服从高斯分布，将采样粒子的均值作为高斯分布的均值，方差为高斯分布的方差，则重要性概率密度为，而新生的粒子由检测到的新目标的模型获得，因此有：

式中：lk－1是存活的粒子数;rk是新产生的目标数目。粒子的权值递推公式如下：

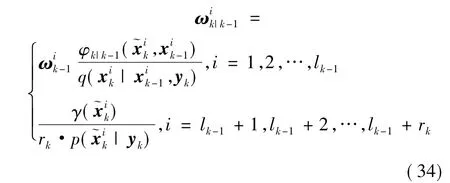
2.5 概率假设密度函数的预测与更新

通常情况下，衍生目标产生的概率是极小的，在这里可以忽略，预测后的概率假设函数包含存活的部分与新生的部分，表示如下：

存活部分的均值与方差的计算方式如式(8)～式(10)所示。

将两项结合之后可表示为：

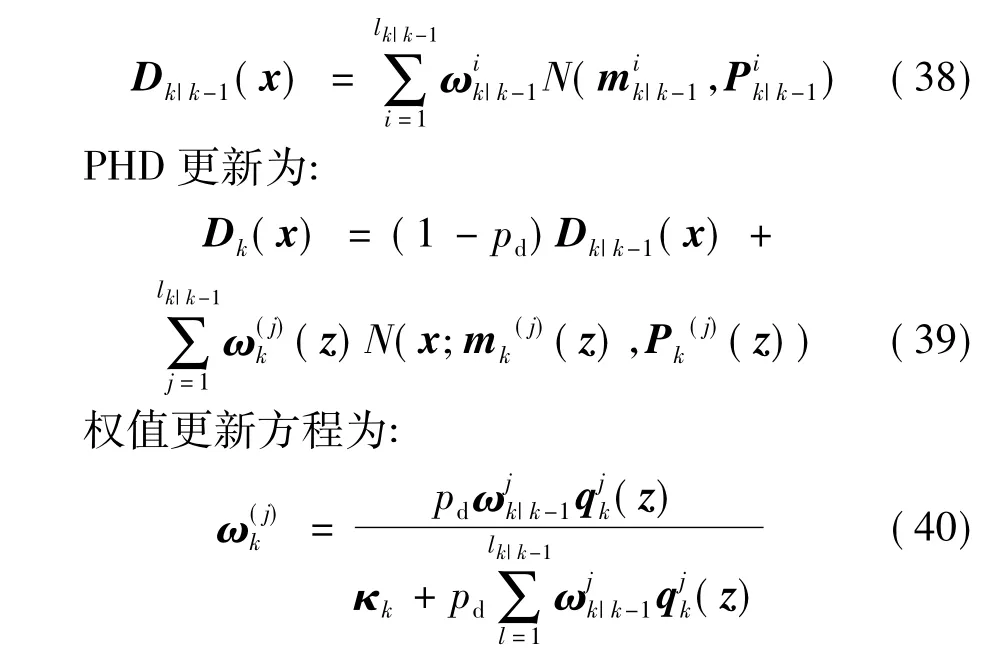
均值与方差的具体计算方式与式(12)～式(13)保持一致。

2.6 目标个数的估计与更新

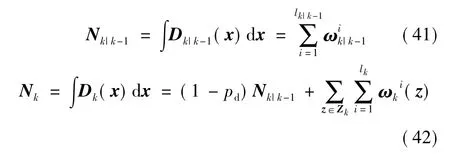
3 仿真实例

3.1 仿真环境

为了验证所提算法的有效性，利用Matlab进行实验仿真，对改进后的U-GMPPHD算法和GMP-PHD算法的仿真结果进行了对比。实验在二维平面区域里进行，采样周期设为1 s，仿真时间为50 s;跟踪的目标是3个，且这3个目标的位置随着时间的变化而变化;实验中的检测概率与目标的存活概率均为0.95，并且服从泊松分布的杂波在每个采样周期里的平均数为30，粒子数设为1 000个。

系统的状态变量为(xk1，xk2，xk3，xk4)，其中(xk1，xk3)是目标的位置，(xk2，xk4)为目标速度，目标初始状态分别为(100，100，3 000，－100)，(100，100，－3 000，100)，(150，100，3 500，0)。实验中，目标的运动模型表示如下：

3.2 仿真结果

在上述仿真环境下，分别用这两种算法对这3个目标进行跟踪，仿真结果如图1～图3所示。图1表示了使用两种算法的目标平均跟踪轨迹示意图;图2是目标个数估计的对比图;图3是位置误差的滤波对比图。

图1 目标跟踪轨迹滤波图

由图1可以看出，使用U-GMPPHD进行滤波后，传统的算法中会出现失跟的情况，改进后得到的目标轨迹相比于传统的GMP-PHD更为精确。图2为经过估计后的目标个数滤波图，由图可以看出，相比于GMP-PHD滤波方法，改进后的方法使得对目标个数的估计更加精确。图3为滤波的位置滤波误差对比图，由图可以看出，经过改进滤波后，位置误差相比于传统算法来说有了明显的改进，系统的稳定性也进一步增强。

图2 目标个数估计

图3 滤波误差图

4 结论

文中首先探讨了在高斯混合粒子PHD滤波算法的基础上，结合了无迹变换进行改进，这种算法在跟踪过程中采用无迹卡尔曼滤波算法进行重要性采样，得到重要性密度函数，仿真结果表明了改进算法的精度相比于高斯混合粒子PHD滤波有了很大的提高，系统稳定性也进一步增强，得到了预期的效果。

［1］Ronald R P S.Multitarget Bayes filtering via first-order multitarget moments［J］.IEEE Transaction on Aerospace and Electronics System，2003，39(4)：1152-1178.

［2］Mahler R.A theoretical foundation for the Stein-Winter probability hypothesis density(PhD)multitarget tracking approach，ADA 400 161［R］.2000：99-117.

［3］Ozgur Erdinc，Peter Willett，Yaakov Bar-sharlom.A physical-space approach for the probability hypothesis density and cardinalized probability hypothesis density filter［C］∥Proceeding of the SPIE Conference on Signal and Data Processing of Small Targets，2006，6236.

［4］周承兴，刘贵喜，侯连勇，等.改进的高斯粒子概率假设密度滤波算法［J］.控制理论与应用，2011，28(7)： 1005-1008.

［5］郝艳玲，孟凡彬，周卫东，等.多目标跟踪的高斯混合概率假设密度滤波算法［J］.弹箭与制导学报，2010，30(3)：35-39.

［6］Vo B N，Singer S，Doucet A.Sequential Monte Carlo implementation of the PHD filter for multi-target tracking［C］∥The 6th International Conference on Information Fusion，Cairns，Queensland，Australia，2003.

［7］王晓，韩崇朝.用于机动目标跟踪的多模型高斯混合概率假设密度滤波器［J］.控制与决策，2012，27(12)： 1864-1869.

［8］Clark D，Vo B T，Vo B N.Gaussian particle implementations of probability hypothesis density filters［C］∥2007 IEEE Aerospace Conference.Big Sky MT，2007：1-11.

［9］孟凡彬，郝艳玲，张崇猛，等.基于无迹粒子PHD滤波的序贯融合算法［J］.系统工程与电子技术，2011，33 (1)：30-34.

［10］张诗柜，朱立新，赵义正.粒子滤波算法最近进展与展望［J］.自动化技术与应用，2010，29(6)：1-9.

［11］王晓，韩崇朝，连峰.基于随机有限集的目标跟踪方法研究及最新进展［J］.工程数学学报，2012，29 (4)：567-578.

［12］张崇猛，王戈，孟凡彬，等.一种无迹粒子PHD滤波的多目标跟踪算法［J］.系统仿真学报，2013，25 (1)：94-98.

Gaussian Mixture Particle Probability Hypothesis Density Filter Based on Unscented Transform in Multi-target Tracking

LIU Xin1，FENG Xinxi1，KONG Yunbo1，WANG Jing2
(1Information and Navigation College，Air Force Engineering University，Xi’an 710077，China; 2No.94969 Unit，Shanghai 200400，China)

Considering lower estimating accuracy and filtering divergence of traditional GMP-PHD algorithm in clutter environment，a modified GMP-PHD based on unscented transform was proposed.On the basis of the GMP-PHD prediction，the algorithm applies unscented transform to importance sampling，updates the sampling particles combined with observation values to get the importance density function，and then update the GMP-PHD function.The performance of the proposed algorithm was compared with traditional GMP-PHD algorithm.The simulation results show that the proposed algorithm can promote not only the accuracy but also the stability of the system.

multiple target tracking;probability hypothesis density;unscented transform;Gauss hybrid particles PHD

TN953

A

10.15892/j.cnki.djzdxb.2015.05.005

2014-11-19

陕西省自然科学基金(2011JM8023);CEMEE国家重点实验室开放基金(2014K0304B)资助

刘欣(1991－)，女，陕西渭南人，硕士研究生，研究方向：多传感器数据融合、目标跟踪。