带多约束条件的弹道成型中制导律设计*

常冠男，王钺，陈韵，江婷婷，马清华

(1清华大学电子工程系，北京 100084;2中国兵器工业第203研究所，西安 710065)

带多约束条件的弹道成型中制导律设计*

常冠男1，王钺1，陈韵2，江婷婷2，马清华2

(1清华大学电子工程系，北京 100084;2中国兵器工业第203研究所，西安 710065)

实际工程中，低成本导航系统的性能特点决定其不能在全姿态下工作，当空地导弹高空发射打击近程目标时，广义弹道成型中制导律(GTSGL)会导致下滑段弹体俯仰姿态角超出陀螺的测量范围。针对这一问题，文中在GTSGL的基础上通过增加姿态角约束修正项提出了带多约束条件的弹道成型中制导律。仿真表明，所提中制导律在满足中制导末端位置和角度约束的同时能够有效的限制弹体俯仰姿态角，在工程约束条件下具有更理想的中制导性能。

中制导律;多约束;弹道成型

0 引言

现代战争中，使用近程精确制导空地导弹执行空对地打击已经成为攻击敌方的主要手段。导弹飞行过程中，超视距的工作条件使其必须采用初制导+中制导+末制导的复合制导体制，其中，中制导段的主要作用是把导弹导引到能保证末制导可靠截获目标的预定区域内，为了给导引头捕获目标创造良好的条件，中制导段在引导导弹飞向中末制导交接点的同时还要使得导弹在交接点处具有理想的飞行状态，目前有关中制导律的研究工作主要考虑了中制导末端的位置和弹道倾角这两个约束条件［1-4］。

实际工程中，成本低可靠性高的三自由度燃气陀螺仪经常作为测量弹体姿态的主要制导部件，但其性能特点决定了其不能在全姿态下使用，同时当弹体姿态角较大时支架误差也会对测量精度产生重要影响。因此，姿态角限制也成为工程中中制导律设计的重要约束条件。当导弹高空发射打击近程目标时，广义弹道成型中制导律的特性会使得导弹在中制导初始段以大俯仰姿态角飞行，甚至超出陀螺的有效测量范围。文中针对上述工程问题，在广义弹道成型中制导律的基础上提出一种带多约束条件的弹道成型中制导律，该中制导律通过增加姿态角约束修正项，使得中制导段能够同时满足位置、弹道倾角及弹体姿态角的约束条件，并且保留了末端弹道需用过载接近于零的优良特性，具有比广义弹道成型中制导律更好的综合性能，提高了导弹武器系统打击近程目标的作战能力。

1 广义弹道成型中制导律性能分析

制导系统线性简化动力学模型如图1所示，其中at表示目标加速度，ac表示按照中制导律计算得到的加速度指令，am为弹体加速度响应，假设弹体为理想环节，飞行速度保持不变。

图1 制导系统线性简化动力学模型

制导系统的状态方程可以表示为：

式中：x为状态变量;F为状态矩阵;G为控制矩阵，且：

为使得导弹在中末制导交接点处几何关系达到最佳，进而有利于导引头搜索捕获目标，选择中末制导交接点处的位置和弹道倾角作为约束条件。文献［4］中已经证明在速度恒定的情况下，弹道倾角约束可以转化为法向速度约束，故终端约束条件为：

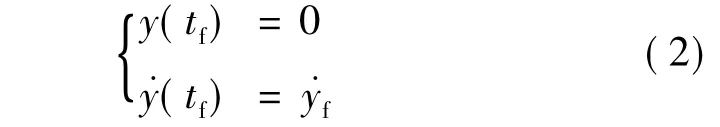
除此之外，为了给导引头捕获目标创造更加理想的环境，希望导弹在接近交接点时需用过载尽量小甚至接近于0，有利于交接段的平稳过渡。故在以加速度平方积分最小为目标函数的基础上，引入剩余时间的幂函数作为权函数：

式中：n表示制导阶次;tgo表示导弹剩余飞行时间。则目标函数为：

式中：tf为导弹飞行总时间，从目标函数的形式可知，当n＞0时，为使得目标函数极值存在，必有因此，该目标函数可确保当制导阶次大于零时中制导段末端需用过载为零。在小视线角假设条件下，根据图2中弹目交汇几何关系，可推导出便于工程实现的广义弹道成型中制导律如式(5)。

图2中，v(t)表示导弹速度，R(t)表示弹目相对距离，vr表示弹目相对接近速度，θ(t)表示弹道倾角，q(t)表示弹目视线角，qf为期望落角，具体推导过程见［5-6］。式(5)表明该导引律由三部分组成，第一项是确保命中位置的比例导引项，第二项是确保命中落角的角度约束项，第三项是目标机动加速度补偿项。

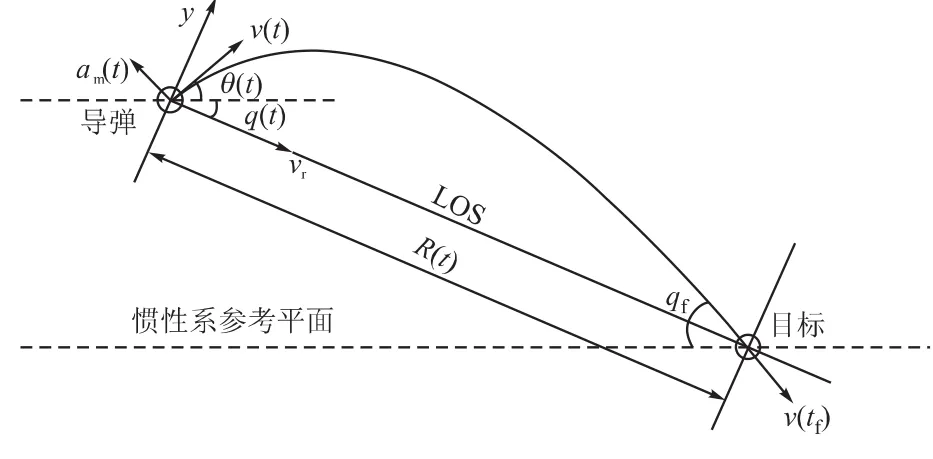
图2 弹目交汇几何关系

文献［5］中有如下结论：广义弹道成型中制导律能够引导导弹精确飞向中末制导交接点，并且在交接点处落角满足约束条件;制导阶次n大于0时，可使得中末制导交接点处需用过载趋近于0，制导阶次n越大，初始段弹道需用过载越大，初始段弹道越弯曲，同时末段弹道需用过载越小，末段弹道越平直;取制导阶次n=1，可保证在中末制导交接点处弹道需用过载为零，为导引头捕获目标创造良好的条件，同时又使得中制导初始段弹道需用过载不至于过大，有利于工程实现。

广义弹道成型中制导律能够减小中末制导交接点处的需用过载，有利于导引头捕获目标，但这一特性决定了中制导段必须采用先快速下压再转平飞的弹道形式。当导弹高空发射打击近程目标时，中制导初始段的快速下压会使得导弹以大俯仰姿态角飞行，甚至超出陀螺的有效测量范围，如某型燃气陀螺仪的有效测量范围为－60°～60°，导弹在6 000 m高度发射打击12 km目标时中制导段弹体俯仰姿态角曲线如图3所示。

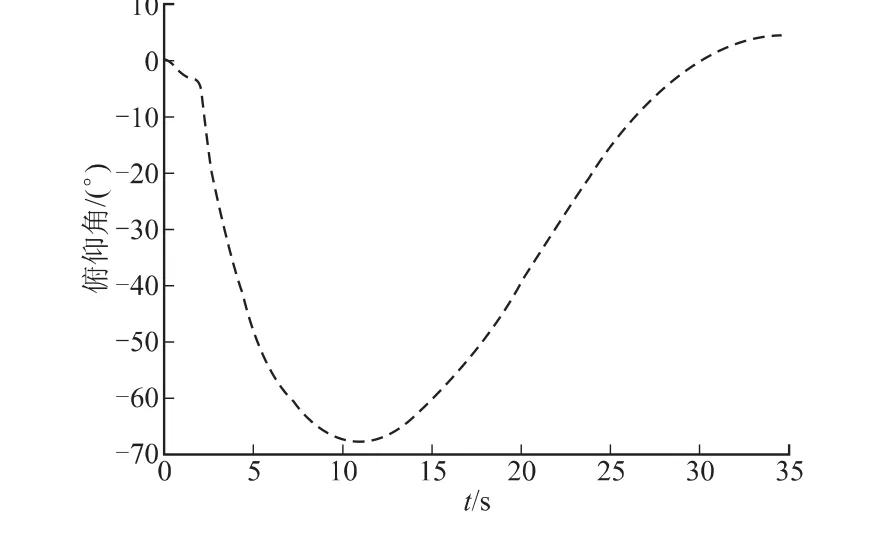
图3 中制导段俯仰姿态角曲线

曲线表明，弹体俯仰姿态角最大达到－68°，已经超出了陀螺的有效量程。因此广义弹道成型中制导律在取得交接点处过载较小这一性能优势的同时带来了导弹打击近射程目标能力的损失，限制了武器系统的作战效能。

2 多约束条件下弹道成型中制导律设计

分析发现，为了给转平飞段留有足够的距离和时间以减小交接点处需用过载，中制导初始段通过大过载下压将导弹快速的调整到有利于实现落角的方向，进而导致弹体俯仰姿态角过大。因此，当导弹俯仰姿态角接近边界条件时，考虑采取措施对指令加速度做出调整，设调整后的制导指令为：

式中：ac0为原广义弹道成型中制导律(generalized trajectory shaping guidance law，GTSGL)的制导指令;aG为限制俯仰姿态角的修正项指令(pitching angle restriction item，PARI)。设弹体俯仰姿态角为θ，陀螺有效量程为－η～η，弹道倾角为θ，攻角为λ，速度为v，为研究弹体姿态角收敛条件，构造如下Lyapunov函数：

式(9)表明，当弹体俯仰姿态角逐渐接近陀螺有效量程时，只要使得修正指令与俯仰姿态角反号且足够大，就可以保证俯仰姿态角收敛。

设计限制俯仰姿态角的修正项表达式如下：

式中：μ为开关阈值;k2为修正项增益系数。

从修正项表达式可以看出，在姿态角从开关阈值逐渐增加到边界的过程中，修正项分子逐渐增大，分母逐渐减小，修正项从0增大到无穷大，即修正项对姿态角的限制作用随着姿态角的增大而增大，能够有效限制弹体俯仰姿态角不超过边界条件;同时开关阈值的引入还使得在开关切换过程中指令连续平滑过渡，避免了切换过程中的颤振。

综上，带多约束条件的弹道成型中制导律表达式为：

3 仿真分析

针对导弹高空发射打击近程地面目标的典型场景，设置仿真条件如下：导弹初始位置为(0 m，6 000 m)，初始速度为0.6 Ma，初始射角为0°，导弹最大可用过载为5 g，中末制导交接点位置为(8 000 m，350 m)，交接点处期望弹道倾角为0°，下滑段弹体俯仰姿态角约束为－60°～60°。设置kp=6，kq=6，kt=0，μ =50，η=60，k2=1.2，采用六自由度弹道仿真程序对初制导段及中制导段进行仿真，仿真结果如图4～图7所示。

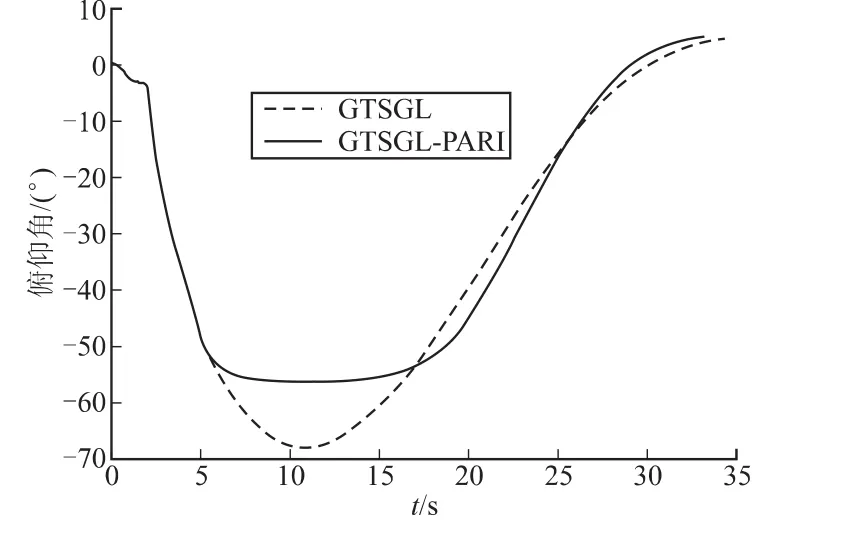
图4 俯仰角曲线对比

图5 弹道曲线对比

图6 弹道倾角曲线对比

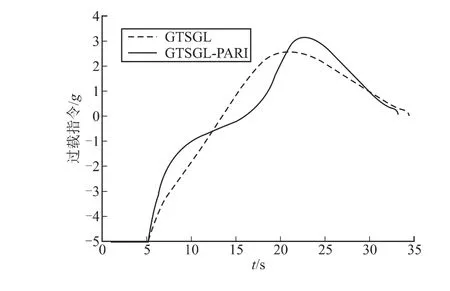
图7 纵向过载指令曲线对比

仿真结果表明：带多约束条件的弹道成型中制导律能够有效的限制下滑段弹体俯仰姿态角在约束范围内;导弹在中末制导交接点处弹道倾角为零，满足中制导末端的位置约束和角度约束条件;过载指令曲线表明新中制导律同样使得中制导末端弹道需用过载较小，保留了广义弹道成型中制导律这一优良性能。

综合弹道曲线、弹道倾角曲线、过载曲线可以看出，姿态角约束修正项在当弹体姿态角超过开关阈值时开始起作用，使过载指令绝对值逐渐减小，导弹下滑趋势变缓，控制弹体姿态角不超过边界条件。当弹体姿态角逐渐远离边界条件时，修正项作用逐渐减弱，位置约束项、角度约束项作用逐渐加强，以确保满足弹道末端的位置和角度约束条件。因此，带多约束条件的弹道成型中制导律在弹体俯仰姿态角不超过开关阈值时，其性能与原广义弹道成型中制导律相同;当导弹高空发射打击近程目标时，能够有效的限制下滑段弹体俯仰姿态角在约束范围内。

本质上，广义弹道成型中制导律在中制导初始段利用大过载将弹目相对位置调整到有利于实现落角的方向，进而实现终端过载趋近于零;而带多约束条件的弹道成型中制导律则综合考虑了位置和落角约束、姿态角约束以及终端过载性能，使得过载能力在中制导期间得到了更合理的分配，更加合理的利用了导弹的过载能力，因此在实际工程约束条件下取得了更为理想的中制导性能。表1给出了某型空地导弹分别使用GTSGL与GTSGL-PARI两种中制导律的近射程打击能力对比。

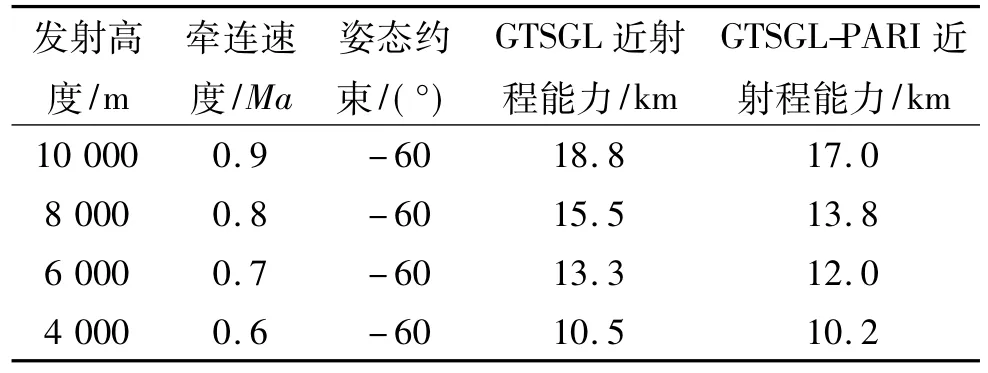
表1 近射程打击能力对比

仿真结果表明：带多约束条件的弹道成型中制导律极大的提高了导弹武器系统打击近程目标的作战能力。

4 总结

文中针对实际工程中的姿态角约束问题，对弹道成型中制导律在高空发射场景下性能衰退的原因进行深入分析，通过增加姿态角约束修正项提出了带多约束条件的弹道成型中制导律。仿真结果表明，所提中制导律在满足中制导末端位置和角度约束条件的同时能够有效的限制弹体俯仰姿态角，并且保留了末端弹道需用过载接近于零的优良特性，具有比广义弹道成型中制导律更好的综合性能，提高了导弹武器系统的近射程打击能力。

［1］SHIH-MING YANG.Analysis of optimal midcourse guidance Law［J］.IEEE Transaction on Aerospace and Electronic Systems，1996，32(1).

［2］窦磊，窦骄.带多约束条件的次最优中制导律设计［J］.宇航学报，2011，32(12)：2505-2509.

［3］P A RAJU.Empirical virtual sliding target guidance law design：An aerodynamic approach［J］.IEEE Transactions on Aerospace and Eelectronic Systems，2003，39(4).

［4］刘丹，祁载康.限制导弹落角和落点的最优制导律［J］.北京理工大学学报，2003，21(3)：218-281.

［5］刘大卫，夏群利，崔莹莹，等.具有终端位置和角度约束的广义弹道成型制导引律［J］.北京理工大学学报，2011，31(12)：1408-1413.

［6］Zarchan P.Course on missile guidance，israel association for automatic control［C］.Israel：IAAC，2009.

［7］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京：北京理工大学出版社，2011.

Trajectory-shaping Guidance Law Design with Multi-constrain

CHANG Guannan1，WANG Yue1，CHEN Yun2，JIANG Tingting2，MA Qinghua2
(1Department of Electronic Engineering，Tsinghua University，Beijing 100084，China; 2No.203 Research Institute of China Ordnance Industries，Xi’an 710065，China)

In practical engineering，the properties of low-cost navigation system determine that it can't work at all attitudes.When air-toground missile launched in high-altitude to attack short-range targets，the prominent characteristic of generalized trajectory-shaping guidance law(GTSGL)could result in pitching angle beyond the measurement range of gyro sensor in glide trajectory.Concerning this problem，a new trajectory-shaping guidance law with multi-constraint was proposed in this paper.This new guidance law can limit pitching angle by adding pitching angle restriction item on the basis of GTSGL.Simulation result shows that the proposed midcourse guidance law can effectively limit the pitching angle and meet impact position and angle constraints，which has more ideal midcourse performance under engineering constraints.

midcourse guidance law;multi-constrain;trajectory-shaping

TJ765.3

A

10.15892/j.cnki.djzdxb.2015.05.009

2014-09-28

常冠男(1990－)，男，吉林公主岭人，硕士研究生，研究方向：导弹制导与控制。