《三角形内角和》教学实践与反思
韦珍萍

【关键词】三角形内角和 教学实践 教学反思
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2015)06A-0084-02
教学内容:人教版四年级下册第85—86页《三角形内角和》。
教学目标:
1.让学生通过猜想、验证等一系列的操作活动,推理归纳出三角形的内角和是180°。
2.让学生通过小组合作动手操作探究获取知识。
3.培养学生灵活应用获取知识解决实际问题的能力。
教学重点:
合作探究发现“三角形内角和是180°”这一知识的形成,以及应用它来解决问题。
教学过程:
一、知识链接
师:在我们学过的三角形中,如果按边长分,你知道有哪些三角形?
生1:有等边三角形。
生2:有等腰三角形。
生3:有直角三角形。
师:如果按角分呢?
生1:有锐角三角形。
生2:有钝角三角形。
生3:有直角三角形。
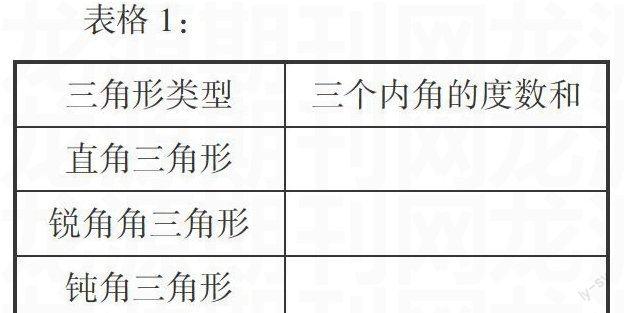
学生回答的同时,教师把学生的答案填入相应表格中(见表格1)。
【反思】此环节设计从学生已有的知识出发,让学生回忆学过的知识,而教师用表格的形式串联知识,形成知识网络,便于学生对比理解。
师:你知道三角形有几个内角?拿出三角板相互指出三个内角给你的同桌看看。
(随后教师用课件演示画出三角形内角,让学生更加明确内角的位置)
师:有谁知道你手上这两个三角板三个内角的度数分别是多少呢?
生1:90°、60°、30°。
生2:90°、45°、45°。
(生已学过三角板的三个内角)
学生回答时,教师把答案填入相应的表格中(见表格2)。
师:同学们算算这两个直角三角形的三个内角的度数和是多少?
生:180°。
(教师相应地填在表格上)
师:这是直角三角形,它的内角和是180°,是不是任意一个三角形的内角和都是180°呢?同学们猜猜看。
生1:也是180°。
生2:不一定。
……
师:请同学们任意画一个你喜欢的三角形,然后用量角器分别量出每个内角的度数,并算出三个内角的度数和,在小组中展示你们的结果,然后各小组汇报。
生1:我画的是锐角三角形,三个内角度数和是179°。
生2:我画的是钝角三角形,三个内角的度数和是181°。
生3:我画的是等腰三角形,三个内角的度数和是180°。
(师相应填入表格中)
……
师:请观察表格中各类三角形内角和,你们有什么发现?
生:发现内角和都接近180°。
【反思】此环节设计从学生已有知识经验出发,从特殊三角形内角和类推到猜想任意三角形内角和,从而引导学生探索新知。从独立思考到小组交流再到全班汇报,各种学习方式有机结合、相互补充,学生思维开始从无序走向有序。
师:这是什么原因呢?到底三角形内角和的准确度数是多少呢?用什么方法来验证呢?
师(提示):把我们手中三角形的三个角剪下来拼一拼,看看你们有什么发现?
生1:我发现三个角拼成了一个平角,等于180°。
生2:我不用剪,我把3个角折下拼在一起也成了一个平角,等于180°。
师:同学们通过拼一拼、折一折,发现任意一个三角形内角和等于180°。那么,请看表格中同学们量得的数据,为什么它们都不全等于180°呢?
生1:我们量得不准。
生2:我们的量角器不够标准。
师:对,这就是误差。
教师播放课件再次验证,得出结论:三角形内角和等于180°(全班齐读这一结论)。我们发现了三角形内角和等于180°这一特性有什么用呢?
【反思】此环节设计让学生先猜想后验证。学生在拼一拼、折一折、看一看课件演示等一系列的数学活动中,小组合作能力、动手能力、交流能力都得到了培养,同时体会到了成功的快乐。
二、解决问题
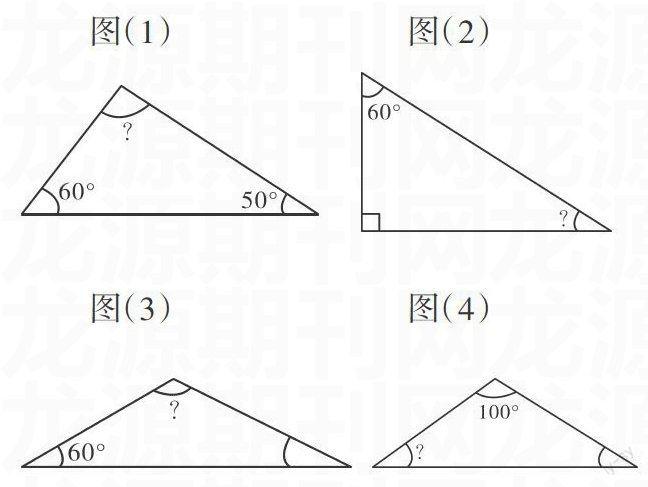
师:请同学们运用这一特性解决以下四个问题(出示四个图)。
【反思】先用课件出示图(1),∠1=60° ∠2=50° 求∠3=?学生会马上想到运用三角形内角和这一特性解决问题。随后出示图(2),∠1=65° 求∠2=?学生在思考后也很快完成。最后再出示图(3),这是一个等腰三角形,底角=35°求:顶角=?图(4),这是一个等腰三角形,顶角=100°求∠1=?学生都要经过比较长时间的思考才能完成。
师:这里有几块被打碎的三角形玻璃钢板,只剩下完整的一个角,你能判断它是哪类三角形吗?
【反思】以上练习设计呈阶梯式,教师根据学生的学习和认知特点,设置了基础题、提高题和开放题(第三块玻璃钢板),适合所有学生的需求,让他们体会到成功的喜悦。其中开放题由于所给条件包含答案不唯一的因素,因而学生在判断的过程中必须利用已有知识,结合有关条件,从不同的角度对问题做全面分析,才能做出正确判断。这一过程培养了学生的思维,同时也让学生感受到数学问题就在自己的身边,进而主动参与问题的解决。
三、总结全课(略)
【反思】“动手实践、自主探索、合作学习”是学生学习数学的重要手段。本课教学设计以这一基本理念为指导,强调“以学生为中心、自主探究为主线”而展开教学。纵观本课教学:1.教学设计层次清晰,循序渐进,从学生已有的知识(回忆已学过的三角形类型)出发,通过实物教具(三角板、量角器等)引导学生在理解的基础上探究三角形的内角。2.整节课始终围绕:“猜想—验证—运用”这一主题展开教学,学生在“猜想任意三角形内角和是否都等于180°”这一悬念中产生学习兴趣,进而主动去探索求证,激发了求知欲。在求证过程中,学生通过拼一拼、折一折、看一看等一系列的数学活动,发现了“任意三角形内角和等于180°”这一结论。这是由学生自己发现、探索得来的知识,学生在亲身经历中理解、掌握了三角形的内在规律和联系,从而在运用这一知识来解决问题时也就游刃有余。在这一系列教学过程中,学生得到了动脑、动手实践、自主探索的机会,并在充分经历知识产生和发展的过程中培养了探究能力,建立了学习自信心,激发了求知欲望,获得了成功体验。3.在验证拼角操作时,笔者发现有些学生在拼角的过程中花费的时间较多,而有的学生会以三角板的边为一条线来拼角,也有的学生直接把三角形的三个角折拼在一起成平角。如果能避免学生拼角耗时多这一弊端,在课前预习时就布置学生在家长的帮助下先试着拼一拼,上课时再让学生在小组内合作拼,形成帮扶,效果可能就会更好一些。
(责编 黎雪娟)

