应用FFT计算△Σ调制器信噪比的分析
欧书琴,陈 军
(安徽三联学院 电子电气工程学院,安徽 合肥 230601)
应用FFT计算△Σ调制器信噪比的分析
欧书琴,陈 军
(安徽三联学院 电子电气工程学院,安徽 合肥 230601)
针对许多设计者存在错误使用快速傅里叶变换计算△Σ调制器输出信号信噪比的问题,在分析△Σ调制器工作原理和推导计算△Σ调制器信噪比理论模型的基础之上,详细地阐述了使用快速傅里叶变换计算△Σ调制器信噪比和绘制其功率谱密度的过程。以二阶△Σ调制器为例,在MATLAB®和Simulink®环境中完成了信噪比的计算和功率谱密度的绘制,实验结果证明了所述方法的正确性,对正确设计△Σ调制器具有重要的实际应用价值。
△Σ调制器;信噪比;过采样;噪声整形;窗函数;功率谱密度;噪声带宽
△Σ调制器(Delta-Sigma Modulator, DSM或Sigma-Delta Modulator, SDM)因采用过采样和噪声整形技术提高有用信号频带内的信噪比而被广泛地应用在高精度的场合,如模数转换器(Analog to Digital Converters, ADC)、数模转换器(Digital to Analog Converters, DAC)、频率综合器、数字射频和高精度振荡器等[1-4]。随着金属氧化物半导体(Complementary Metal Oxide Semiconductor, CMOS)技术的发展,如何设计和实现高性能△Σ调制器成为当前研究的热点[5]。
信噪比(Signal-to-Noise Ratio, SNR)是衡量△Σ调制器性能的主要指标之一,是设计与实现过程中重点考虑的参数[6-8]。△Σ调制器的输出是包含有用信号和量化噪声的离散时间序列信号,通常使用快速傅里叶变换(Fast Fourier Transform, FFT)来分析输出数据的功率谱密度(Power Spectral Density, PSD)和SNR,已有的工作都是笼统地给出分析结果,没有详细地阐述计算步骤。导致很多设计者在使用FFT处理输出数据的过程中存在一些概念运用不当的问题[8]。因此,在文献[8]的基础之上,以二阶△Σ调制器为例详细阐述如何正确使用FFT估计SNR和绘制PSD,具有十分重要的实际应用价值。
1 △Σ调制器信噪比的计算
应用FFT能很方便地计算出周期信号的功率谱,然而由于△Σ调制器的复杂性、非线性和混沌性,其输出数据是带有随机量化噪声的非周期离散时间序列,因此不能直接使用FFT计算其功率谱。以图1所示的二阶△Σ调制器在正弦信号激励条件下的输出数据为例,阐述如何正确地应用FFT估计其SNR和PSD[8]。
1.1 量化噪声线性化模型
量化器是△Σ调制器中的非线性组成部分,在对输入信号进行量化时会引入量化误差。量化器两个邻近输出量化值之间的差值称为量化步长长度(step size)Δ,两个邻近输入阈值之间的差值称为最低位长度(Least-Significant Bit size, LSB size)。量化器输出的最大值与最小值之差称为量化器的全量程(Full Scale, FS)[8]。

ue=0
(1)
(2)
把量化误差e等效为加性噪声可得如图2所示的线性化模型,其z变换域方程为
V(z)=STF(z)U(z)+NTF(z)E(Z)=U(z)+(1-z-1)2E(z)
(3)
其中信号传输函数(Signal Transfer Function, STF),STF(z)=1噪声传输函数(Noise Transfer Function, NTF)满足
NTF(z)=(1-z-1)2
(4)
令z=ejω代入(4)得
(5)
其中ω表示圆周频率,f′为归一化频率。由公式(5)可知,△Σ调制器的噪声传输函数具有高通滤波器特性,抑制低频的量化噪声且将其放大至高频处,此为△Σ调制器的噪声整形特性,它使低频信号保持完整而高频噪声可以很容易地被滤除。同时,△Σ调制器采用了过采样技术,记信号的最高频率,即带宽为fB,则过采样率(OverSampling Ratio, OSR)表示为
(6)
由于量化误差为白噪声且其频带宽度为fs,则其功率谱密度Se(f)为
(7)
经△Σ调制器整形后的噪声功率谱密度Sens(f)为
(8)
(9)
若输入幅度为A的正弦激励信号,其功率为A2/2,则二阶△Σ调制器的信号量化噪声比(Signal-to- quantization-noise ratio, SQNR)为[8]
(10)
1.2 窗函数的选择
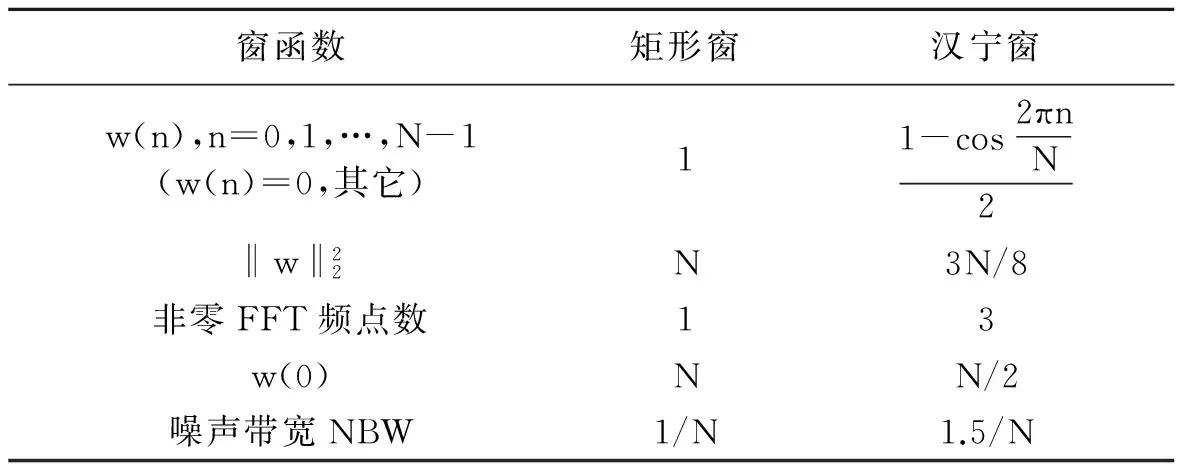
表1 矩形窗和汉宁窗的特性
因为计算机只能处理有限长序列,所以必须对△Σ调制器的输出数据v(n)进行截断,即对其乘以一个N点长度的窗函数w(n)得到信号序列s(n)
s(n)=v(n)w(n)
(11)
根据傅里叶变换性质,时域的乘积对应于频域的卷积,若s(n)、v(n)和w(n)的傅里叶变换分别为S(ω)、V(ω)和W(ω),则有
(12)
为了得到精确的功率谱,在选择窗函数时,必须使由频域卷积引起的误差尽可能地小,在此考虑矩形wrect(n)和whann(n)汉宁两种常用窗函数[9-10]。
窗函数的主瓣影响信号频谱的频率分辨率、边瓣引起频谱泄漏。△Σ调制器的输出数据v(n)包含近似白噪声的量化噪声,边瓣和噪声频谱的卷积会严重影响信号带内的信噪比,称为噪声泄漏(noise leakage)。因此选择边瓣小、衰减快的汉宁窗。作为对比,矩形窗和汉宁窗的特点如表1所示。由离散傅里叶变换(Discrete Fourier Transform, DFT)的理论,将W(ejω)在频域抽样,抽样点数仍为N,那么每邻近两点之间的频率间隔为2π/N,抽样的频点(frequency bins)为
ωk=2πk/N (k=0,1,…,N-1)
(13)
窗函数的长度对信噪比的估计具有影响。计算信噪比的一种简单方法就是计算信号频点上的信号功率与带内噪声频点上的噪声功率之比。一方面,为了计算的准确性,要求信号所占频点数要小于带内总频点数的20%,以确保影响小于1dB[8]。如表1所示,汉宁窗的信号占3个频点,带宽fB内至少包含15个频点,代入式(6)可得
N≥30·OSR
(14)
另一方面,由于随机信号的FFT本身是一个随机量,所以根据FFT计算得到的信噪比也是一个随机量。数值实验表明当N=30·OSR时,计算的信噪比的标准方差大约是1.4dB;当N=64·OSR时,计算的信噪比的标准方差大约是1dB。由于以上两方面考虑,取N=64·OSR比较合适[8]。
1.3 正弦激励信号
在信号处理中,常用正弦信号作为试验信号,以检验某个算法或数字装置的性能,其时域表达式为
x(t)=Asing(2πf0t)
(15)
傅里叶变换的表达式为
X(jΩ)=jπA[δ(Ω+Ω0)-δ(Ω-Ω0)]
(16)
由式(16)知,正弦信号的频谱是位于±f0处的δ函数,这一特点决定了对正弦信号采样时将会遇到一些特殊的现象,因此在△Σ调制器的仿真中频率f0必须选择在FFT的频点上,否则会产生信号泄漏(signal leakage),f0与距其最近频点的距离越远,泄漏越严重[8-10]。不失一般性,以长度为N的矩形窗为例进行阐述,当f0位于FFT的频点上时,即满足
(17)
正弦信号傅里叶变换的圆周频率ω0为
(18)
式(16)用圆周频率表示为
X(ejω)=jπA[δ(ω+ω0)-δ(ω-ω0)]
(19)
式(19)与矩形窗的频域表达式相卷积得到用矩形窗截断后的正弦信号的傅里叶变换Xrect(ejω)
(20)
把式(13)代入式(20)可知,只有当k=m时,Xrect(ejω)不为零,即信号只占据一个频点,不产生信号泄漏。如图3所示,当式(17)满足时,无信号泄漏到其他频点上,而当(17)不满足时,有信号泄漏到其他频点上。汉宁窗的信号应该占据3个频点,其理论推导同矩形窗。
1.4 归一化与噪声带宽
正弦信号x(n)与窗函数w(n)在时域相乘完成对信号的截断,相应于频域的卷积,卷积后信号的幅值为A·W(0)/2,A为正弦信号的幅度,W(0)为窗函数直流处的幅值,由表1可知,W(0)正比于窗函数长度N,如图4所示,当N取不同值时,A·W(0)/2的值也不同,图中信号包含高斯白噪声。因此在绘制频谱时为了统一,通常对频谱幅度进行归一化处理,即对FFT的幅度除以A·W(0)/2,使全量程的正弦波产生0dB的频谱幅值。若全量程范围用FS标记,那么全量程正弦信号的幅度为A=FS/2。因此包含正弦信号序列的FFT归一化的幅度表示为
(21)
Fig.4 Amplitude of the sinusoidal signal of the FFT
单位为dBFS(dB relative to Full-Scale, dBFS)表示参考功率是全量程正弦信号的功率[8]。对图4中的信号进行归一化处理后如图5所示,虽然值不同,但信号的幅值都是0dBFS,然而噪声基底(Noise Floor, NF)的幅值却不同。这是因为信号占据的频点数是固定的(矩形窗1个频点,汉宁窗3个频点),噪声占据所有的频点,总噪声功率为所有频点上噪声幅度的和[8]。因此,当频点数增加时,噪声基底会下降。这个问题可以通过给出噪声带宽(Noise BandWidth, NBW)来解决,归一化后的噪声基底表示内噪声的功率,因此总的噪声功率Pn_total应该为
(22)
其中BW表示总带宽,表示从图中读出的噪声基底,窗函数的NBW如表1所示。在图5中,两种N值下,NBW相差16倍,因此噪声基底NF相差101g(16)=12dB。
1.5 归一化与噪声带宽
在图1所示的二阶△Σ调制器中,量化器的位数为1,即输出+1和-1两个量化值,则FS=2,输入正弦信号的幅度A=0.5,归一化频率为f′=1/512,过采样率OSR=128,汉宁窗的长度为N=64·OSR。按照信号频点(汉宁窗信号占3个频点)上数值的和除以带内噪声频点上数值的和的计算方法,计算出的信噪比为SNR=90dB接近式(10)的计算值。根据前述方法在Simulink®中完成图2所示调制器的仿真,在MATLAB®中完成信噪比的计算和功率谱密度的绘制,绘制的频谱如图13所示[11]。
2 结束语
在总结相关工作的基础上,针对△Σ调制器输出数据的特点,详细阐述了使用快速傅里叶变换计算信噪比和绘制功率谱密度的过程,对正确设计出高性能的△Σ调制器具有重要的实际应用价值。
[1]Shahrukh Athar, Muhammad Ali Siddiqi, Shahid Masud. Design and FPGA Implementation of a 2nd Order Adaptive Delta Sigma Modulator with One Bit Quantization [C]. 20th International Conference on Field Programmable Logic and Applications (FPL), Milano, Italy, IEEE Computer Society Test Technology Technical Council, 2010.
[2]M T Nguyen, C Jabbour, C Ouffoue, et al. Direct Delta-Sigma Receiver: Analysis, Modelization and Simulation [C]. 2013 IEEE International Symposium on Circuits and Systems (ISCAS), Beijing, China, IEEE, 2013.
[3]Liu Liyuan, Li Dongmei, Wang Zhihua. A 0.6-V to 1-V Audio △Σ modulator in 65 nm CMOS with 90.2dB SNDR at 0.6-V [J]. VLSI Design, 2013, 2013: 1-9.
[4]Katara A, Bapat A V, Chalse R, et al. Development of one bit Delta-Sigma analog to digital converter [C]. 2012 Fourth International conference on computational intelligence and communication networks (CICN). Mathura, India, IEEE, 2012.
[5]Lota J, Al-Janabi M, Kale I. Nonlinear Model-Based Approach for Accurate Stability Prediction of One-Bit Higher-Order Delta-Sigma Modulators [J]. IEEE Transactions on Instrumentation and Measurement, 2013, 62(4): 686-692.
[6]Palagiri H V, Makkena M L, Chantigari K R. Performance Analysis of First Order Digital Sigma Delta ADC [C]. 2012 Fourth International Conference on Computational Intelligence, Communication Systems and Networks (CICSyN). Phuket, Thailand, 2012.
[7]R Maghrebi, M Masmoudi. Parameters Estimation of Σ△ modulators Models using a Combined Optimization Algorithm in MATLAB Environment [C]. 7th International Conference on Design & Technology of Integrated Systems in Nanoscale Era (DTIS), Gammarth, Tunisia, IEEE, 2012.
[8]Schreier R, Temes G C. Delta-Sigma 数据转换器[M].北京: 科学出版社, 2007.
[9]郑君里, 应启珩, 杨为理. 信号与系统(第三版)[M]. 北京: 高等教育出版社, 2011.
[10]胡广书. 数字信号处理理论、算法与实现(第三版)[M]. 北京: 清华大学出版社, 2012.
[11]张志勇. 精通MATLAB 6.5版[M]. 北京: 北京航空航天大学出版社, 2003.
( 责任编辑:窦鹏)
Analysis on Computing SNR of △Σ Modulators Using FFT
OU Shu-qin,CHEN Jun
(Information and Communication Technology Department, Anhui Sanlian College, Hefei 230601,China)
The Fast Fourier Transform (FFT) is widely used to estimate the power spectral density (PSD) and of signal-to-noise ratio (SNR) of delta-sigma (△Σ) data, but is sometimes abused by many △Σ designers. The operation principle of △Σ modulator is analyzed and the theoretical model of SNR of △Σ modulator is derived in this paper. And then, the process of computing SNR and drawing the PSD using the FFT are described in detail. The SNR and PSD of a 2nd order △Σ modulator are computed and drawn respectively in the MATLAB and Simulink environment. The results indicate that the method described is valid and has the practical value for the design of △Σ modulator.
Delta-sigma modulator; Signal-to-noise ratio; Oversampling; Noise shaping; Windowing; Power spectral density; Noise bandwidth
2014-12-23
安徽三联学院科研基金资助项目(2013Z015);安徽省高等教育振兴计划新专业建设项目(2013zytz082)。
欧书琴(1985-),女,安徽省合肥市人,硕士,讲师,主要从事信号与信息处理研究。
TP332
A
1673-8772(2015)02-0057-06

