北斗三号射频芯片中Σ-Δ调制器电路设计
董明月,黄海生,李 鑫,杨 毅
(西安邮电大学 电子工程学院,西安 710121)
0 引言
北斗卫星导航系统(BeiDou navigation satellite system,BDS)是我国着眼于国家安全和经济社会发展需要,自主建设运行的全球卫星导航系统(global navigation satellite system, GNSS),北斗三号全球卫星导航系统即北斗三号(BeiDou-3 navigation satellite system, BDS-3)的开通,标志着我国完成了三步走的发展战略。BDS射频芯片是BDS应用的基础,射频芯片中锁相环频率合成器的作用是产生本振信号,锁相环的输出频率如果出错,会导致整个射频芯片出现异常,故锁相环产生的频率信号准确与否,对射频芯片十分关键[1]。由于环路的众多指标均受锁相环反馈部分的分频器影响,而小数分频器的使用,会出现小数杂散,降低电路性能。所以,本文研究设计加入Σ-Δ调制器,以解决小数杂散,但加入调制器后,不仅会产生结构寄生,还会使调制器的输出频谱噪声变高,因此有必要设计加入成型处理的抖动电路,解决调制器产生的结构寄生及输出频谱噪声变高的问题。
1 小数分频器原理
1.1 锁相环基本原理
传统锁相环是由鉴频鉴相器(phase frequency detector,PFD)、电荷泵(charge pump,CP)、环路滤波器(loop filter,LF)、压控振荡器(voltage controlled oscillator,VCO)和分频器(divider, DIV)5个基本模块组成的反馈系统,如图1所示。
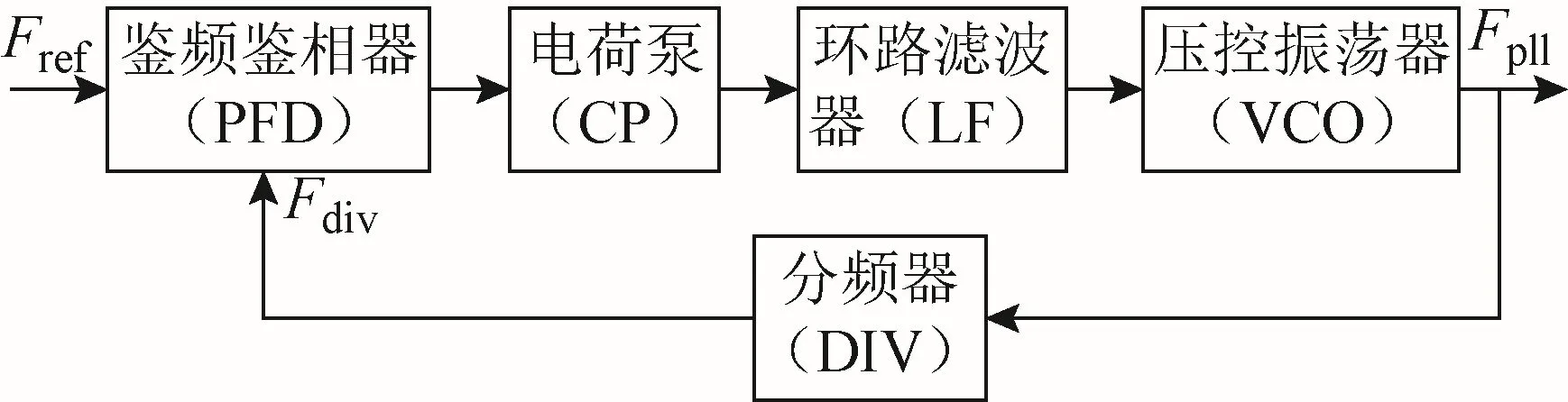
图1 锁相环结构
锁相环电路的工作原理为:输入的参考频率与环路反馈给分频器后的分频结果,通过鉴频鉴相器进行对比并产生脉冲信号,该信号将作用于电荷泵,完成对环路滤波器中的电容充放电,从而通过环路滤波器产生输出电压,对压控振荡器进行控制,进而产生锁相环的最终输出。由于BDS载波频率与晶振频率之间非整数倍关系,所以此处需要设计一个小数分频器。表1列出了BDS-3B1I、B1C、B2a、B2b、B3载波中心频率,与中频频率为3.996 MHz、输入的参考频率为16.369 MHz时对应的分频比(取小数点后4位)。
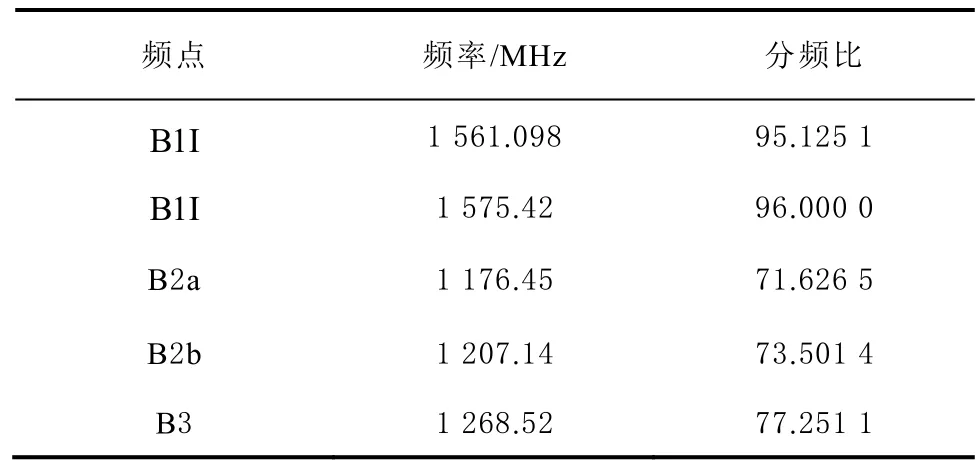
表1 BDS-3载波中心频率及对应分频比
1.2 小数分频器结构
数字电路在实现小数分频时采用平均的方法,小数分频器的每个瞬时是整数分频,但这将导致分频器输出的瞬时频率与参考频率间存在相位差,致使PFD产生锯齿形的相位误差,误差通过环路滤波后作用于VCO[2],使其输出产生杂散。为了使小数分频器的频谱纯度及性能尽可能好,需要处理小数杂散,Σ-Δ调制技术[3]是常用的处理小数杂散的方法。Σ-Δ调制技术通过在小数分频锁相环中加入一个Σ-Δ调制器,运用调制器自身特性,将小数杂散转为量化噪声[4],并将噪声整形到高频段,再利用锁相环本身对输入噪声呈现的低通滤波性将其滤除。这种方法可以从本质上消除小数杂散带来的影响,且易于实现。
Σ-Δ小数分频器[5]的结构框图如图2所示。
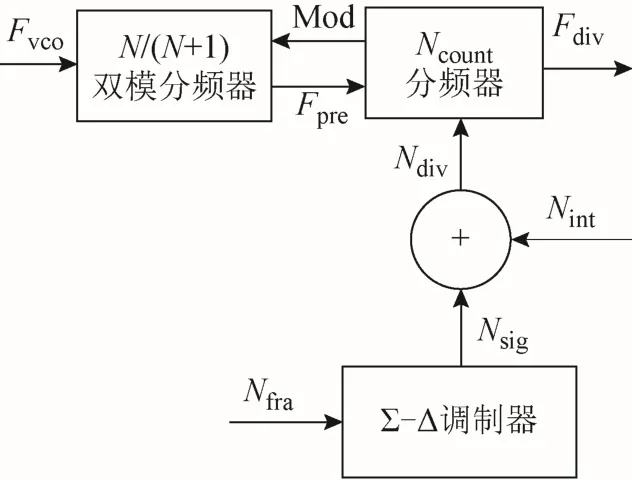
图2 Σ-Δ小数分频器结构
Σ-Δ小数分频器由N/ (N+ 1 )双模分频器、Ncount分频器和Σ-Δ调制器三部分组成。其中,Mod为Ncount分频器反馈给双模分频器的分频模控制信号;Fvco为VCO的输出频率;Fpre为N/ (N+ 1 )双模分频器的输出频率;Fdiv为小数分频器的整体输出;Ndiv为调制序列与整数分频比之和;Nsig、Σ-Δ分别为调制器输出的调制序列;Nint和Nfra分别为预期小数分频比的整数和小数部分。
Σ-Δ小数分频器的工作原理为:输入的小数值作用于Σ-Δ调制器后产生调制序列,调制序列通过与输入的整数值求和后输入到Ncount分频器中,Ncount分频器根据输入的分频比,对双模分频器的输出频率再进行分频,进而产生小数分频器的最终输出频率。
2 MASH 1-1-1型 Σ-Δ调制器
对Σ-Δ调制器进行如下分析:由于一阶调制器[6]在锁相环电路的应用过程中,虽能在一定程度上起到对量化噪声的整形效果,但是低频区仍存在量化噪声,故在电路中一般不采用一阶调制器,而是采用对其进行改进的调制器:将一阶调制器级联到马什(MASH)型的Σ-Δ调制器,会将每级累加器产生的量化误差传递到下一级,需要对量化误差进行二次量化处理,即采用足够多的级数,将量化噪声完全推至高频段的目的[7]。但是多级级联的Σ-Δ调制器,需要等阶数LF的匹配作用才能达到效果,LF设计复杂,且使用韦里洛格·得赫尔(Verilog HDL)实现的高阶Σ-Δ调制器,占用的逻辑资源较多,因此并不是级数越多越好。在实际应用过程中,小数分频锁相环常以采用 4级以下的Σ-Δ调制器为主,但低级Σ-Δ调制器又不能将有用频带内的所有量化噪声推到高频段,故小数分频锁相环多采用3级级联调制器[8],即为MASH 1-1-1型Σ-Δ调制器。
2.1 调制器结构寄生产生的原因
对于MASH 1-1-1型Σ-Δ调制器,在输入小数值时,大部分的输出序列均具有良好的随机性,输出序列频谱曲线平滑;而对于某些特定值,调制器输出序列频谱则会表现出强周期性,具体表现为,在固定频点处出现毛刺,这种现象被称为调制器的结构寄生。
MASH 1-1-1型调制器的输出序列,总有固定的周期性[9],可将 MASH 1-1-1型调制器看作一个有限的状态机,其输出结果的状态跳转由输入值和现态决定,且输出值在固定状态间相互转换。Σ-Δ调制器每一级最小周期的表达式如表2所示。

表2 Σ-Δ调制器每1级最小周期表达式
表 2中:M为量化器的模值;A为输入值;m1[ 0]为第一级调制器的现态;m2[0]为第二级调制器的现态;GCD为求A与M最大公约数的运算符。由每一级最小周期的表达式可以看出,第二级调制器的最小周期L2受第一级调制器输出值的奇偶特性影响,并与输入值A以及量化模值M有关;第三级调制器的最小周期L3受第二级调制器输出值影响。
基于表2进行分析:在三级调制器均不设初值且输入值为奇数时,可以算得L2=L3=2L1,L1= 2a;当输入值为偶数时,L2=L3=2L1,L1= 2a-b。由此得到调制器的输出周期受输入值A的影响较大,且输入值为偶数的输出序列较短,表现为高频时固定频点极高的频谱线,即出现结构寄生现象。经过在先进设计系统(advanced design system, ADS)软件上进行多次仿真发现,结构寄生在A=0.25时尤为明显。
2.2 调制器结构寄生解决方案
MASH 1-1-1型调制器在输入为偶数且各级不设置初值时,会出现结构寄生问题,鉴于其对射频系统的影响,需采取一定的措施对调制器的结构寄生问题进行处理,如随机性方案[10]。通过给调制器加入一个随机的抖动,打破调制器的固有周期,此种方案通过给调制器外接抖动电路实现,电路较简单。
3 抖动电路
3.1 抖动电路的成型处理
调制器结构寄生问题可通过加抖动解决,但伪随机序列的加入,会导致调制器的输出频谱噪声变高,为解决此问题,可通过对输入的抖动做成型处理,结构图如图3所示。
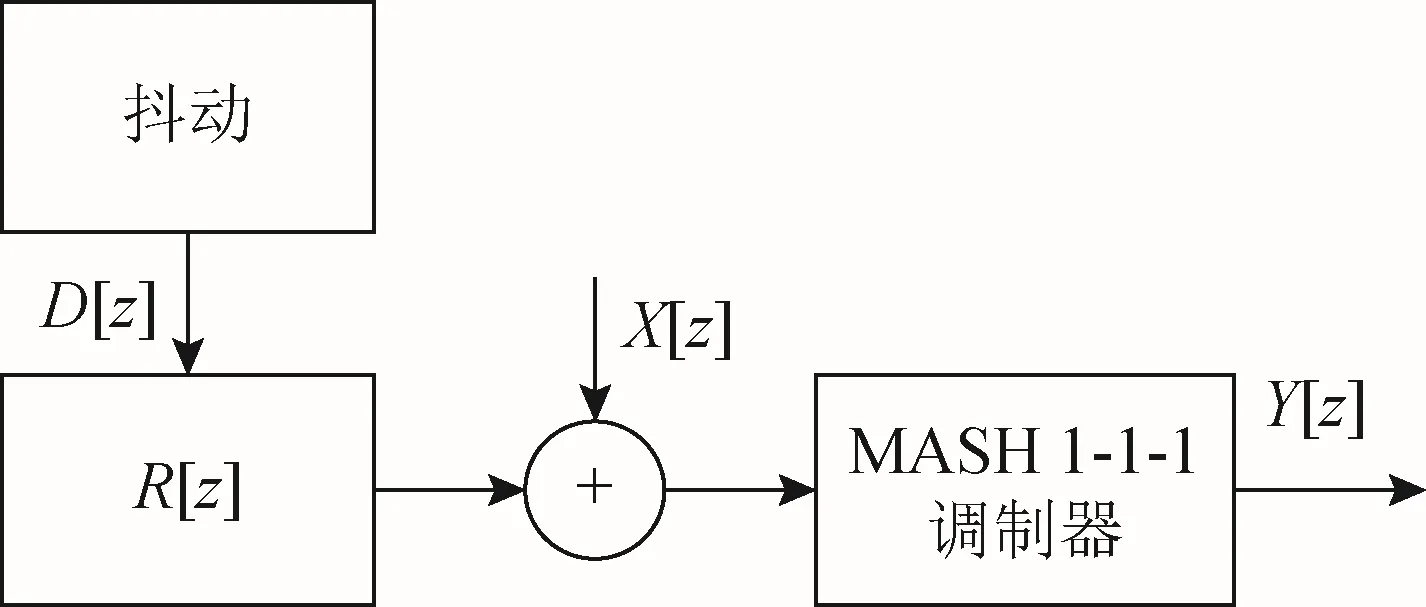
图3 抖动成型处理结构图
图3中:R[z]是成型处理电路;C为阶数。传输函数为
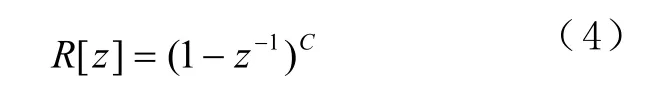
根据 MASH 1-1-1调制器的传递函数[11]及式(4)可得,加入抖动和成型处理电路后的调制器传递函数Y[z]为
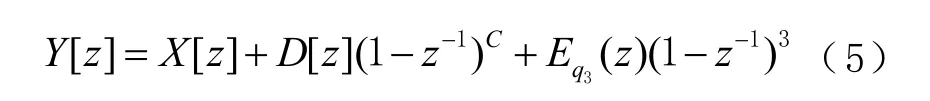
式中:X[z]为输入数值;D[z]为经过成型处理后的抖动;Eq3(z)为量化噪声。从式(5)可以看出,经过成型处理后的抖动D[z]类似于量化噪声被整形到了高频段。
3.2 新映射方法的采用
为了抑制抖动电路引入的带内噪声,需要对抖动电路做成型处理,R[z]的阶数越高,越能抑制抖动电路引入的带内噪声,但是R[z]的阶数过高,会导致其占用过多资源,因此在设计电路时,采用改变序列映射过程的方法,来实现抖动电路的成型处理。
对抖动电路产生的m序列做成型处理的做法,是将m序列输出的0和1映射成“-1、1”。现对映射进行改进,选取24阶m序列中3个移位寄存器(Reg)的输出,将其映射为“-2、-1、0、1”,然后采用一阶R[z]做成型处理,改动示意图如图4所示。
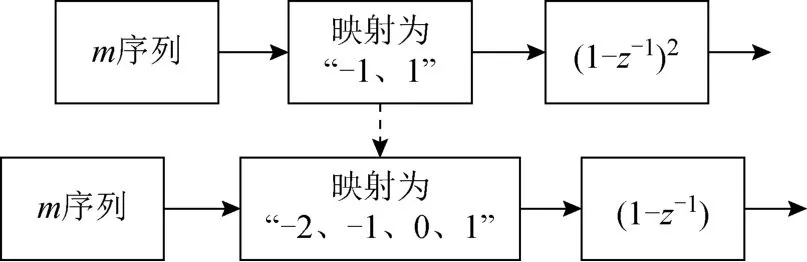
图4 采用新映射方法的抖动电路
采用小数分频比为0.125 1、0.626 5、0.501 4和0.251 1对比新旧两种映射方法。首先,将ADS软件中的小数值设置为0.125 1、0.626 5、0.501 4和0.251 1,然后分别采用“-1、1”映射和“-2、-1、0、1”映射,对m序列二阶成型处理和一阶成型处理进行仿真,仿真结果如图5至图8所示。
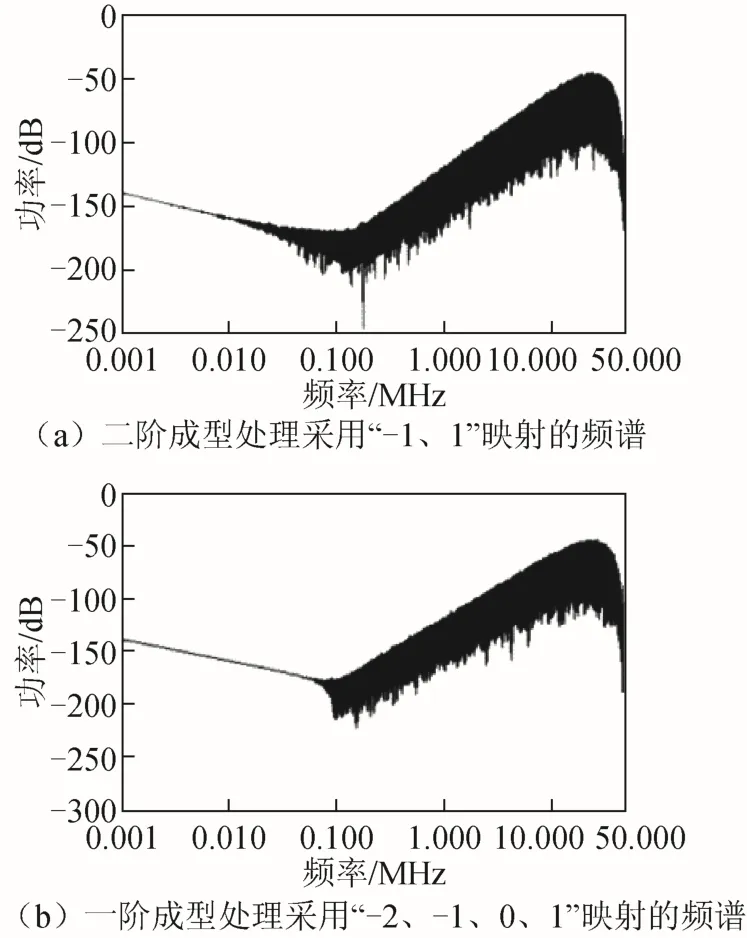
图5 小数为0.125 1时调制器输出序列的频谱

图6 小数为0.626 5时调制器输出序列的频谱
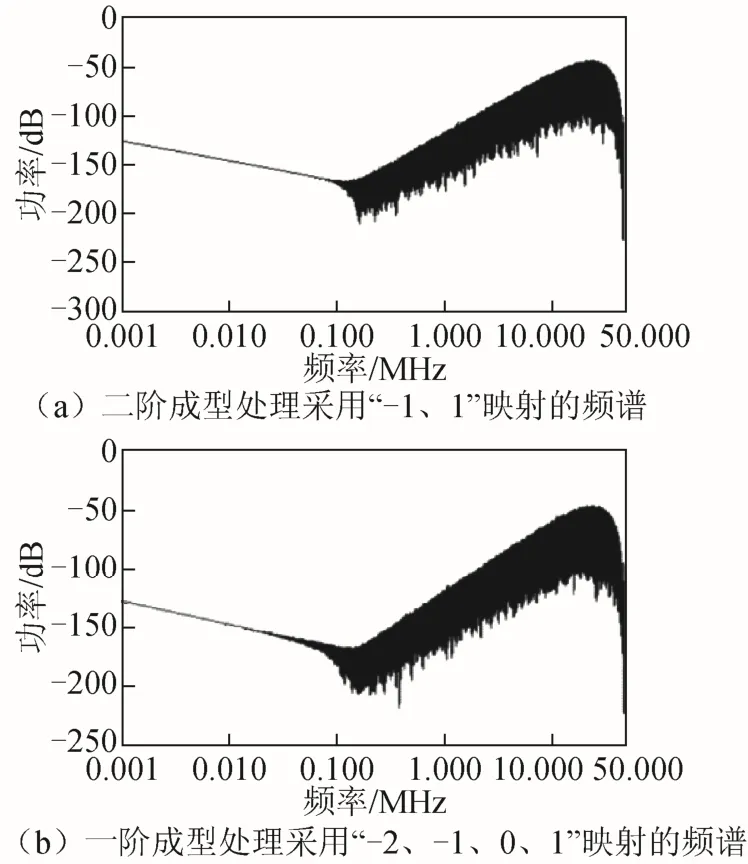
图7 小数为0.501 4时调制器输出序列的频谱
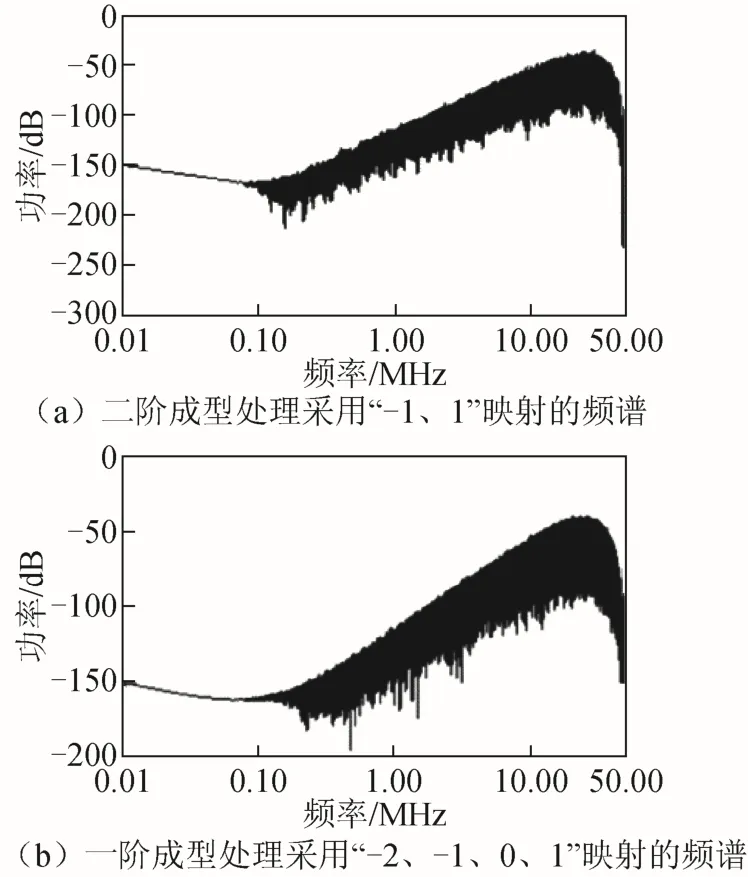
图8 小数为0.251 1时调制器输出序列的频谱
从图5至图8可以看出,使用改进后的新映射方法,进行一阶成型处理的结果与原映射方法进行二阶成型处理的结果相比较,改进后的结果更好。
3.3 电路建模仿真
由于A=0.25时结构寄生尤为明显,分别对仅加入调制器,加入抖动电路的调制器,对抖动做成型处理的调制器进行仿真,结果如图9所示。
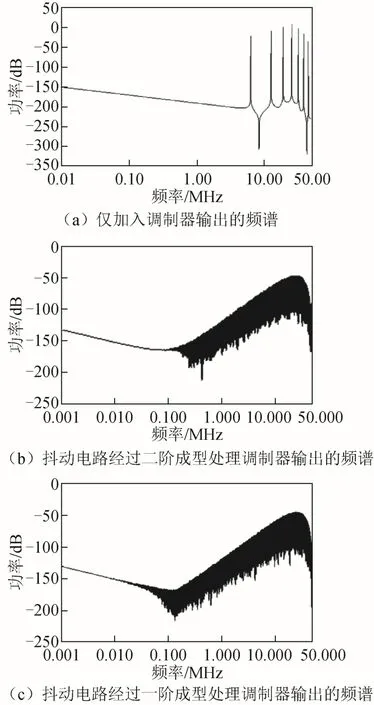
图9 小数为0.25时调制器输出序列的频谱
图9(a)为仅在小数分频器中加入调制器,可以看到,高频时固定频点出现极高的频谱线,即结构寄生现象;图9(b)为对抖动进行二阶成型处理,采用“-2、-1、0、1”映射的调制器,可以看到结构寄生现象明显得到了抑制;图9(c)为对抖动进行一阶成型处理,采用“-1、1”映射的调制器,可以看到结构寄生现象也明显得到了抑制且比图9(b)效果好。
4 电路实现与仿真验证
4.1 MASH 1-1-1型调制器电路
一个寄存器和累加器构成一阶Σ-Δ调制器。根据一阶调制器的逻辑电路,可得MASH 1-1-1型调制器的电路结构[12]如图10所示。
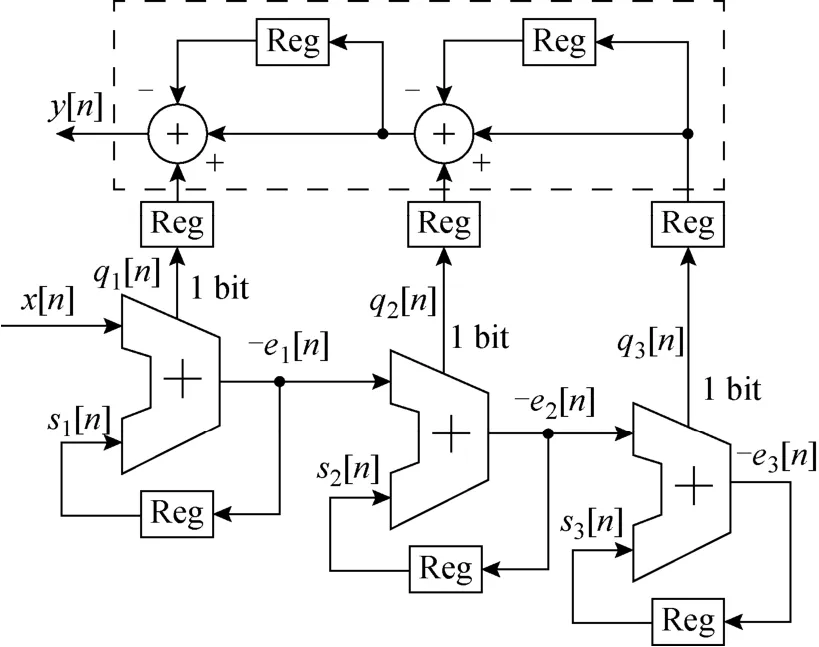
图10 MASH 1-1-1型调制器逻辑电路
图10中:虚线框中的噪声整形电路和三个级联的累加器构成 MASH 1-1-1调制器电路;s1[n]至s3[n]为各个寄存器的输出;q1[n]至q3[n]为进位值;-e1[n]至 -e3[n]为调制器引入的量化噪声。为保证电路时序同步且减少因延时产生的毛刺,在噪声整形电路和累加器之间加入一级寄存器。根据图8可以写出z域表达式为
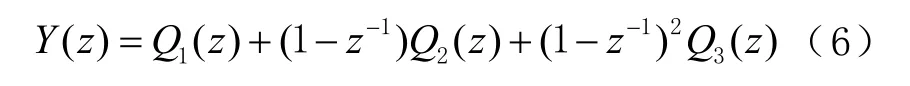
式中:Y(z)为调制序列;Q1(z)至Q3(z)分别为产生的进位值。根据式(6),写出噪声整形电路的时域离散函数为
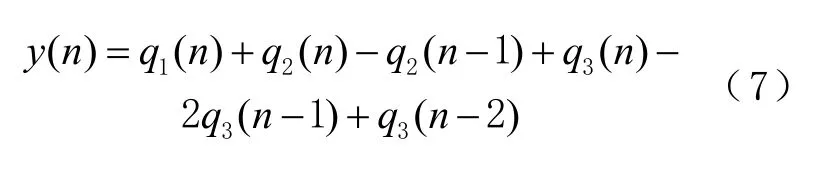
将式(7)整理为F(n) =q1(n) +q2(n) +q3(n),T(n) =q2(n- 1 ) + 2q3(n- 1 ) +q3(n- 2 ),故电路实现时,先分别求F(n)与T(n),再求F(n)-T(n)。
4.2 抖动电路
抖动电路的设计采用24阶m序列[13],使用新的映射方法,且对抖动电路的输出进行一阶成型处理,具体电路逻辑图如图11所示。
如图11所示,成型处理电路和m序列产生电路构成抖动电路。且24阶m序列的特征多项式为
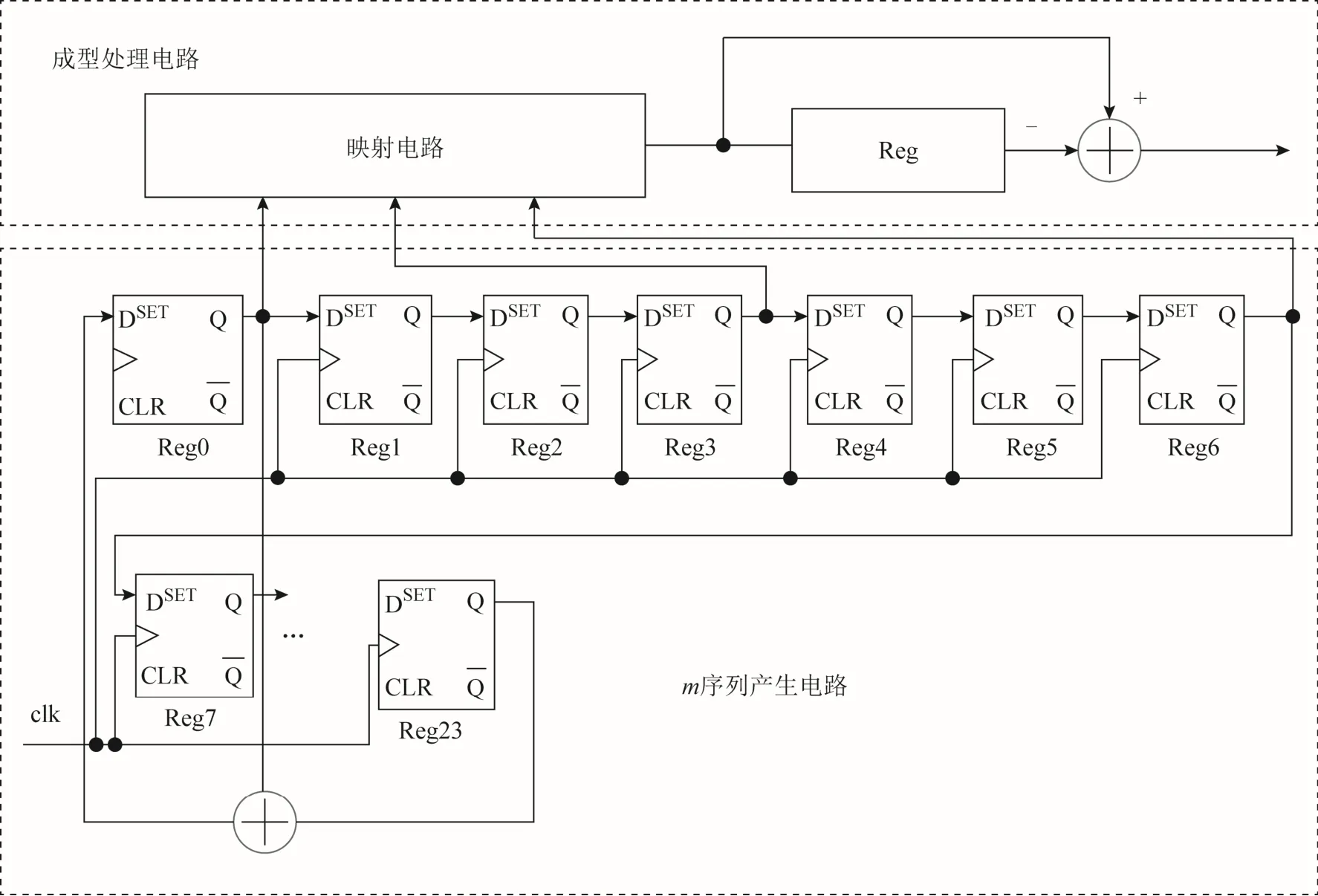
图11 抖动电路逻辑
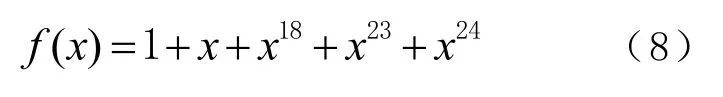
4.3 仿真验证
为验证所设计 Σ-Δ调制器的性能,对电路在莫德尔西姆(Modelsim)软件中进行仿真。由表1可知,BDS-3载波中心频率对应分频比分别为95.125 1,96,71.626 5,73.501 4,77.251 1。由于 96是整数,所以采用其余4个分频比进行验证。因为所设计的调制器累加器位数为20 bit,将输入到电路中的小数部分进行转换,B1I载波中心频率对应分频比的小数0.125 1表示为N_frac=20’d131176,B2a载波中心频率对应分频比的小数0.626 5表示为 N_frac=20’d656932,B2b载波中心频率对应分频比的小数0.501 4表示为 N_frac=20’d525756,B3载波中心频率对应分频比的小数 0.251 1表示为 N_frac=20’d263297,电路的行为级仿真结果如图12所示。

图12 小数分频器的仿真结果
5 结束语
为解决小数分频器产生小数杂散的问题,在小数分频器中加入Σ-Δ调制器。另外,加入经过成型处理的抖动电路,解决了调制器产生的结构寄生及输出频谱噪声变高的问题。其中,抖动电路采用新的映射方法。研究表明:Σ-Δ调制器的加入,有效地抑制小数杂散对锁相环输出频率的干扰;经过成型处理且采用新映射方法的抖动电路,不但能抑制调制器本身结构寄生问题,还能降低抖动电路引入的噪声对电路输出结果的影响。可将此调制器用于BDS-3射频芯片中,以改善芯片性能。

