相电流差突变量选相在混压同塔输电线跨电压故障中的适应性分析

刘 欣 黄少锋 张 鹏

(1.新能源电力系统国家重点实验室(华北电力大学)北京 102206 2.国家电网公司直流建设分公司 北京 100052)

0 引言

为充分利用线路走廊的输送能量，提高输送能力，电力系统已开始广泛采用混压同塔输电模式［1-3］，同时架线方式造成混压同塔线路跨电压故障成为主要故障之一［4］。对于方向或距离纵联保护，要实现选相跳闸，其选相元件的动作准确性十分重要［5，6］。目前数字式保护常用电流突变量保护包括相电流差突变量选相和相电流突变量选相［7-9］。

混压同塔线路之间电联系大于磁联系时，在电气特征上属于“强电弱磁”系统。相反，当磁联系大于电联系时，则属于“弱电强磁”系统。不同电压等级的同塔系统，可分解为强电弱磁系统和弱电强磁系统两种情况，对这两类系统的故障分析和继电保护的研究都非常重要。在工程中因弱电强磁导致继电保护的不正确动作情况时有发生［8］，本文针对弱电强磁系统跨电压故障中的选相元件进行研究，假设输电线路经过完全换位，三相完全对称。

目前对混压同塔的故障分析方法研究有扩展十二序分量法［9］以及以六序分量法加边界条件扩展［10］等方法，但现有故障分析方法均不能将不同电压等级的同塔四回线完全解耦［11-15］，且对混压同塔四回线中故障选相问题鲜有研究。

本文以发生单相跨单相接地故障中的相电流差突变量选相为例，首先将经典去耦的方法应用于零序阻抗网络对其进行完全解耦，构造复合序网图计算故障电流;并在此基础上计算出了计及不同电压等级两个系统之间零序互感时的相电流差突变量。然后与现场使用的忽略此互感时的相电流差突变量作对比，得到两种情况下的突变量差值，分析此差值，得到相电流差突变量选相的适应性与两系统电源电动势相角的关系。在此基础上可以给出电源电动势相角的指导范围以提高相电流差突变量选相的适应性。最后在一个实际系统中计算出了相电流差突变量适应性与两系统电源电动势相角关系，并在PSCAD 中建立模型进行仿真验证。

1 混压同塔跨电压故障计算

以弱电强磁混压同塔输电线单相跨单相接地的跨电压接地故障为例，使用复合序网图方法进行故障分析。图1为弱电强磁的混压同塔四回线中Ⅰ系统的C相跨Ⅱ系统的a 相短路接地故障。

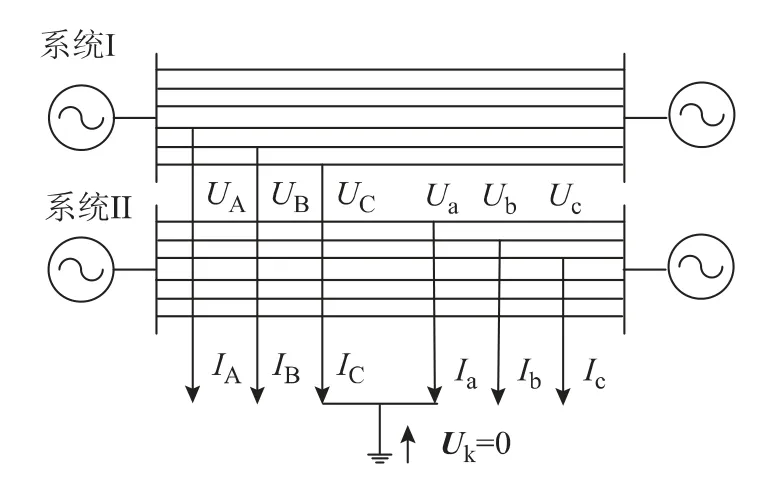
图1 弱电强磁的混压同塔四回线C-a-g 故障模型Fig.1 Model of mixed-voltage four-circuit transmission lines with weak-electric and strong-magnetic condition system with C-a-g fault

假设其中一个电压等级用“系统Ⅰ”表示，其故障线路的三相标注为A、B、C;另一个电压等级用“系统Ⅱ”表示，其故障线路的三相标注为a、b、c。并且所标注的电流、电压均指短路点的电气量;各序阻抗均归并到短路点。本文中电气量下标中的1、2、0分别表示正、负、零序分量，字母则分别对应各相，Ⅰ、Ⅱ分别对应两个电压等级的系统。UK代表短路点的对地电压。Ⅰ系统是高电压等级系统，Ⅱ系统是低电压等级系统。

接地故障时，故障模型中对地电压UK为零。

对于系统Ⅰ，短路点的三相边界条件为

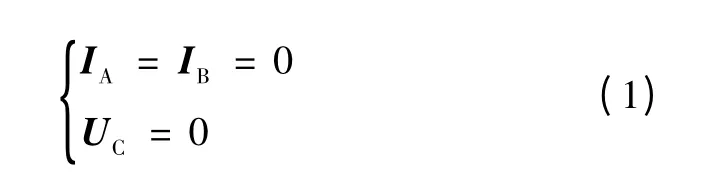
分解为特殊相(C 相)的对称分量，有

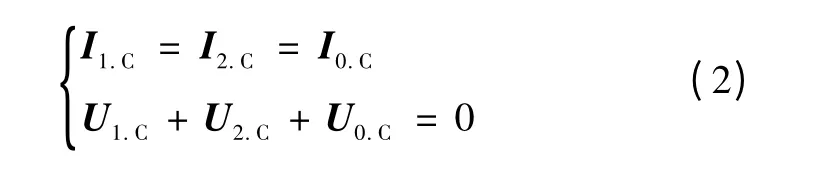
对于系统Ⅱ，a 相是特殊相，系统Ⅱ具有类似形式的边界条件。

从短路点归算正、负、零序网络，由于两系统间的正序阻抗间的互感很小，可以忽略不计，负序网络与正序网络相同。而零序阻抗之间的互感不能忽略不计，采用经典去耦的方法对整个系统的零序网络进行去耦和归算。综合以上过程可以得到正、负、零序阻抗网络如图2所示，详细归算过程见附录。

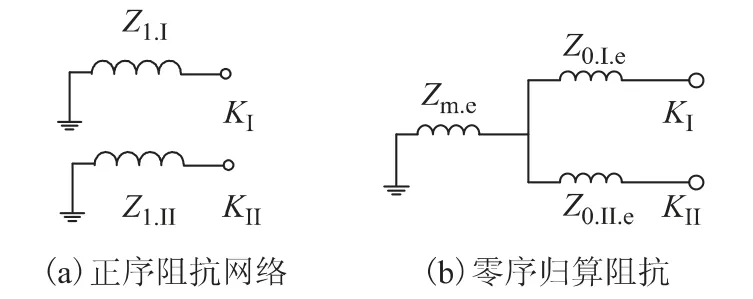
图2 混压同塔四回线的序阻抗网络Fig.2 Sequence networks of four-circuit mixed-voltage transmission lines

负序与正序阻抗相同，零序归算阻抗中的阻抗下标e 代表等效阻抗，连接上述的正、负、零序网络图，并结合UK=0 的条件，可得到C-a-g 故障(单相跨单相接地的跨电压故障)复合序网图如图3所示。

图3 计及互感时C-a-g 故障的复合序网图Fig.3 Composite sequence network of the C-a-g fault including mutual inductance

可得各序电流为

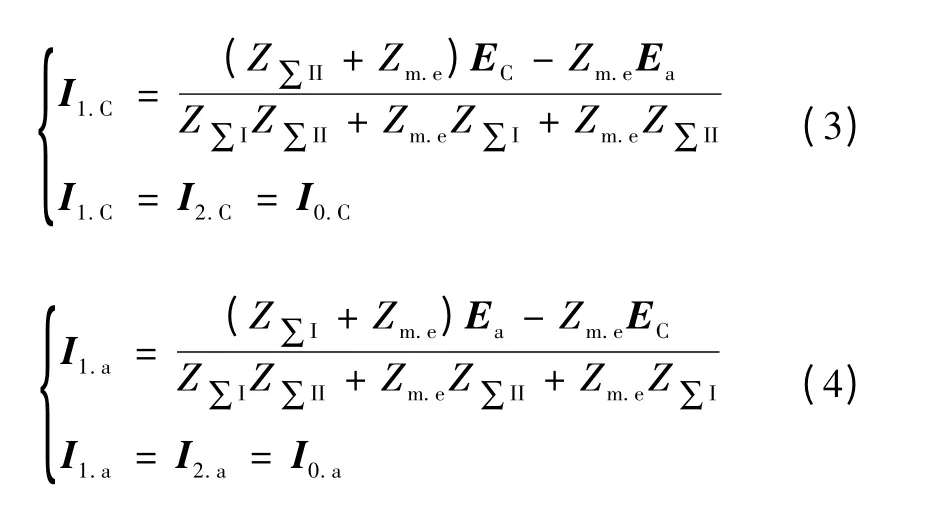
绘制复合序网图的关键点在于两个系统的故障点电压相同。因此，可将两个系统的序网图合并为一个复合序网图。

为了简便、清晰，本文仅绘制出单相跨单相接地跨线故障的复合序网图，实际上，按照上述的基本思想，也可以绘制出混压线路其他跨线故障的复合序网图。

2 相电流差突变量选相

本文以系统Ⅱ为例进行分析。Ⅰ系统C 相跨Ⅱ系统a 相接地短路的故障情况下，Ⅱ系统的测量电流中含有零序分量，判定为接地短路。对于Ⅱ系统，正确选出a 相的典型条件为

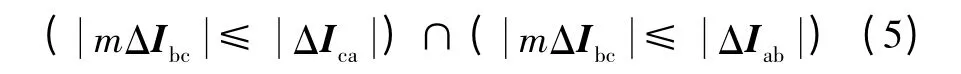
式中m 为整定系数，一般取4～8。其中，计算跨相电流差突变量的过程为

式中α=ej120°。考虑到C1=C2，I1．a=I2．a=I0．a，可简化如式(7)所示，具体推导过程见附录。

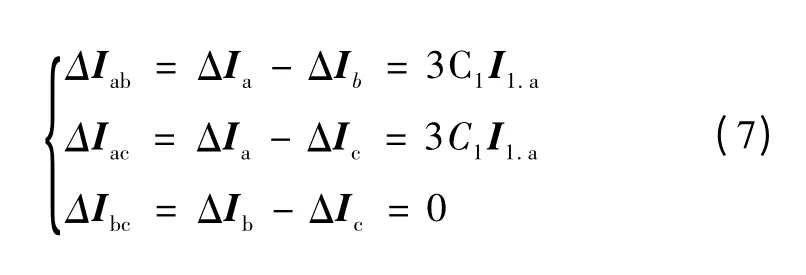
式中:ΔIa、ΔIb、ΔIc为相电流突变量;ΔIab、ΔIac、ΔIbc为相电流差突变量;C1、C2、C0为正、负、零序的电流分布系数。

3 相电流差突变量选相适应性分析

工程实际中的做法是不计不同电压等级系统之间的零序互感，计算的故障电流与实际的故障电流有较大的差别，从而影响线路保护的整定计算以及保护动作的准确性。

在本节中，首先使用第1 节中复合序网络图的方法计算计及其互感时相电流差突变量，然后计算忽略不同电压等级系统之间的互感时的相电流差突变量。将以上两种情况下的突变量作对比，得到两种情况下的突变量差值，分析此差值，得到相电流差突变量选相的适应性与两系统电源电动势相角的关系。

3.1 相电流差突变量计算

1)计及互感时的相电流差突变量。

结合上述第1 节故障分析所得的故障电流特征I1．a=I2．a=I0．a，假设C1=C2，则

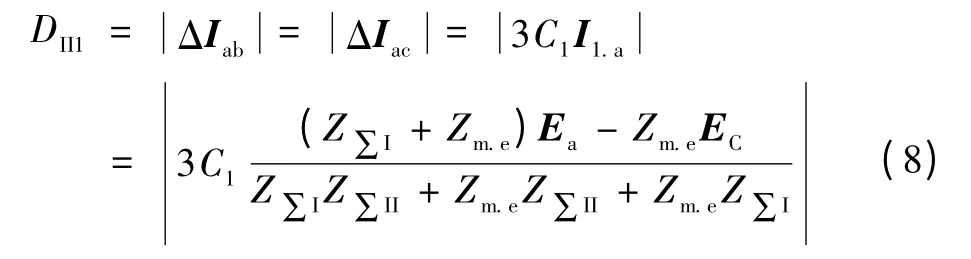
2)不计互感时的相电流差突变量。

忽略不同电压等级之间的互感，对Ⅱ系统，C-a-g(单相跨单相接地的跨电压故障)与a-g(单相接地故障)相同，则

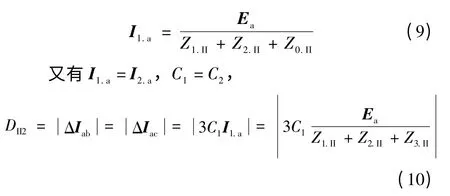
3)差值计算。

计及互感时的相电流差突变量与不计互感时的差值DII计算为

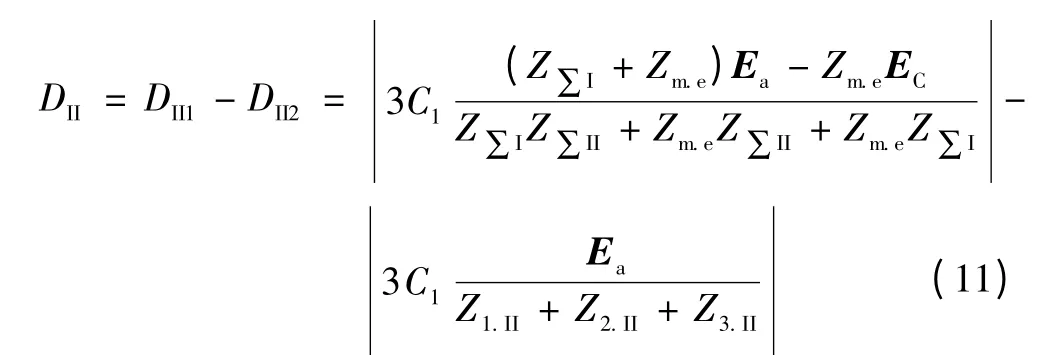
系统Ⅱ的相电流差突变量差值DII是由于Ⅰ系统对Ⅱ系统之间的互感造成的。

由于ΔIbc=0，式(11)体现了不考虑线间互感后的相电流差突变量与准确值之间的差距，能够作为判断选相适应性标准。当DII＞0时，计及互感的相电流差突变量计算值更大，选相更加容易，此时突变量选相元件处于良好的应用条件;当DII＜0时，计及互感的相电流差突变量计算值偏小，选相变困难，此时突变量选相元件的应用效果受到影响。即相电流差突变量选相的适应性与DII的大小密切相关。

3.2 适应性分析

3.2.1 分析DII中的变量

分析式(11)，对于给定系统，故障发生位置确定时，各归算阻抗、电流分布系数确定。运行状态确定时，故障点处的归算电压EC、Ea模值也可确定。

为了简化问题分析，假设故障发生在线路中点，则Ea=EIIcos(δII/2)、EC=EIcos(δI/2)，EI、EII分别为系统Ⅰ、Ⅱ的首端电压有效值，δI、δII分别为两系统首末端的功角差。但EC、Ea的夹角可变，则DII随此夹角的变化而变化。

应指出，故障发生在其他位置时同样可计算得到故障位置处的电压模值。为简单说明方法，以下分析以故障发生在线路中点为例。

则可将EC、Ea的关系表示为

式中:k 为EC、Ea的模值之比，当故障发生位置固定时，k 为已知;δC为EC超前Ea的角度。

3.2.2 DII大小与EC、Ea的夹角关系

设两系统中点电压EC、Ea的相角为δC、δa。以Ⅱ系统的a 相中点电压Ea为参考矢量，δa=0°，则EC、Ea的夹角即为δC，式(11)可写成δC的函数为

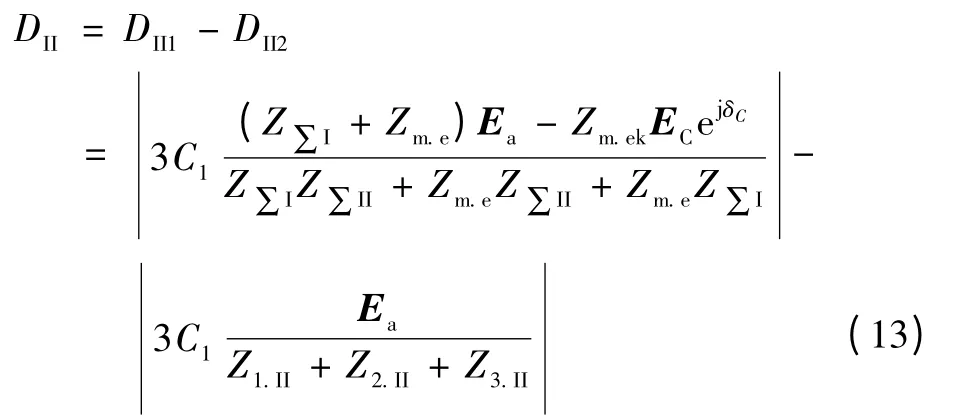
在系统运行方式和故障发生位置固定时，计及系统内各元件的阻抗角几乎相同，则有:①当δC=0时，ejδC=1，DII最小，相电流差突变量之差最小，选相元件处于最差的应用条件;②当δC=180°时，ejδC=－ 1，DII最大，相电流差突变量之差最小，选相元件处于最佳的应用条件。

发生故障位置确定时，对于给定系统可以计算出不同的δC所对应的DII的大小关系。可依次分为如下3 类情况:①DII=0，突变量选相元件应用条件不变;②DII＞0，突变量选相元件处于良好的应用条件;③DII＜0，突变量选相元件的应用效果受到影响。并依次可以求出此时的δC的值域。

3.2.3 DII大小与两系统电源相角关系

图4为混压四回线的单相跨单相接地模型。图中Ⅰ系统的两端电源分别是EIP、EIQ;Ⅱ系统的两端电源分别是EIIP、EIIQ;L1、L2和L3、L4分别是属于Ⅰ、Ⅱ系统的两回线路;KI、KII分别是两个系统的短路点。

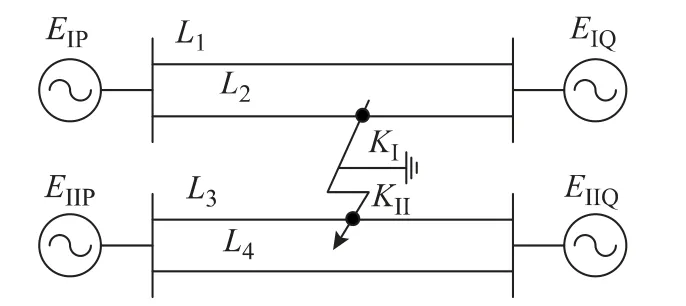
图4 混压同塔四回线路单相跨单相接地故障模型Fig.4 Model of single phase to single phase earthed fault in mixed-voltage four-circuit transmission lines

Ⅰ系统的P 端C 相电压EIPC有效值为EI，相角为δIPC;Q 端C 相电压EIQC有效值为EI，相角为δIQC。

Ⅱ系统的P 端电压a 相电压EIIPa有效值为EII，相角为δIIPa，δIIPa=δII/2;Q 端电压a 相电压EIIQa有效值为EII，相角为δIIQa，δIIQa=－δII/2。

两系统的双侧电源电动势的矢量图如图5所示，则两系统中点电压EC、Ea的相角δC、δa满足

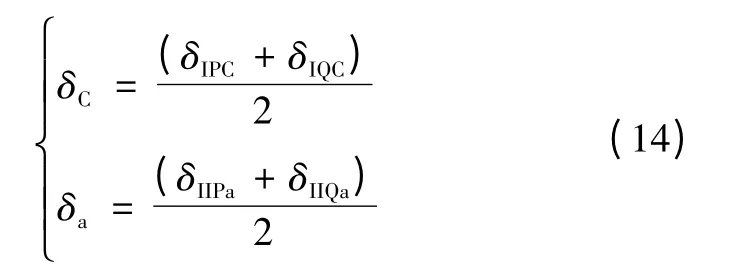
系统运行方式一定时，则两系统的相角差δI、δII为

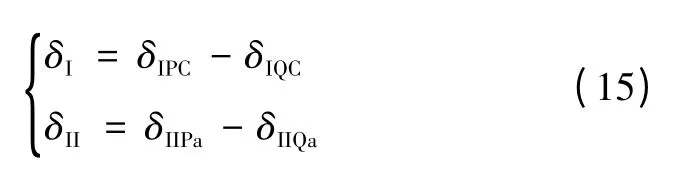
δI、δII已知，δIIPa=δII/2，则δIIQa=－δI/2，δa=0°，δC、δIPC、δIQC为未知数。

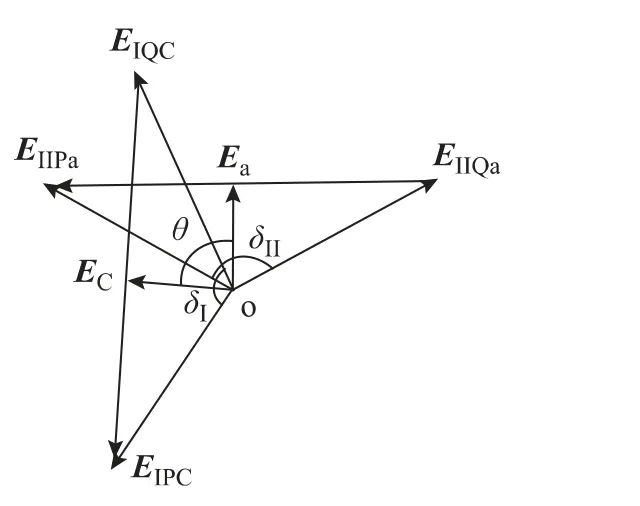
图5 两系统双侧电源及中点电动势Fig.5 Voltage in neutral point/starting point/ending point of the double double sources power system diagram

联立式(14)和式(15)得

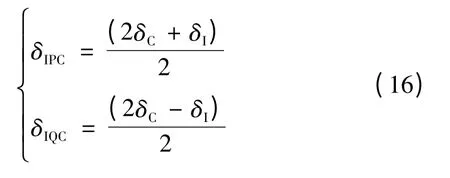
则由以上关系可得到相电流差突变量适应性与Ⅰ系统电动势的相角关系。

4 实例分析

4.1 相电流差突变量计算

在给定混压同塔四回线系统中线路单位阻抗、电源大小，运行状态均是定值，给定系统如下:Ⅰ系统电压等级为500 kV，电源正序阻抗为j18 Ω，零序阻抗为j54 Ω，导线正序单位阻抗为0.007+j0.3 Ω/km，零序单位阻抗为0.266+j1.026 Ω/km;Ⅱ系统电压等级为220 kV，电源正序参数为j70 Ω，零序阻抗为j93 Ω，导线正序单位阻抗为0.01+j0.43 Ω/km，零序单位阻抗为0.301+j1.367 Ω/km;相同电压等级之间的零序互感单位阻抗为0.259+j0.723 Ω/km，不同电压等级系统之间零序互感单位阻抗为0.156+j0.459 Ω/km;线路长度为300 km。仿真条件是送端电源相角超前受端相角60°，假设故障发生在中点，则系统归算参数如表1 所示。

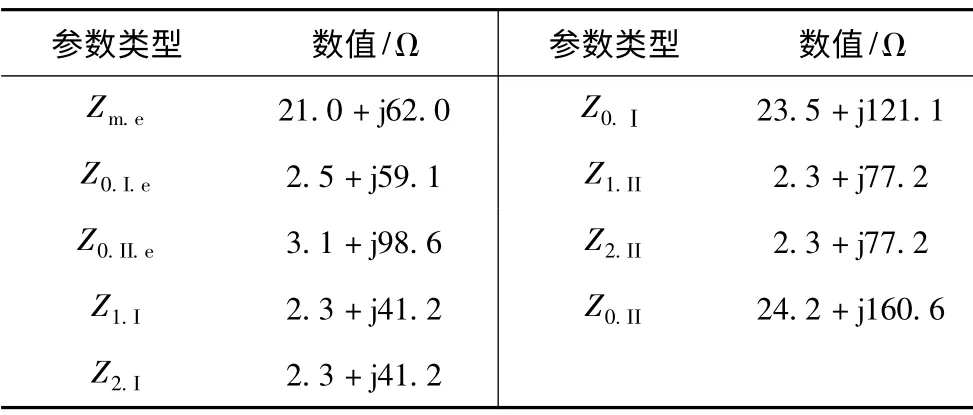
表1 跨电压故障模型参数Tab.1 Parameters of the cross-voltage earthed fault model

则由式(12)可得

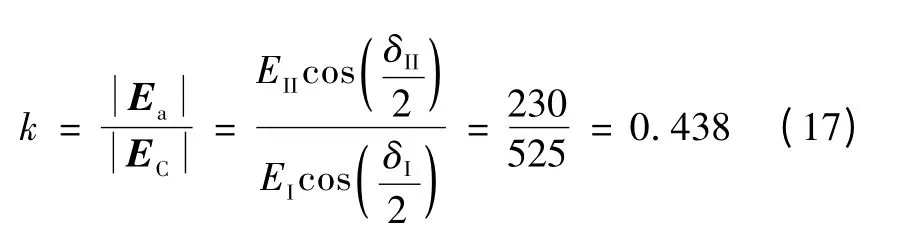
对照表1 可得到式(18)中除δC以外的所有变量的值，DII随δC变化而变化

4.2 DII大小与EC、Ea的夹角δC的关系

当δC在0～360°变化时，DII1、DII2与δC之间的关系如图6所示，实线圆是δC在0～360°变化时DII1的值;虚线圆是δC在0～360°之间变化时DII2的值。使用极坐标画出可更清楚地看出DII1与DII2的大小关系。

图6 DII1与DII2与δC之间的关系图Fig.6 Diagram of relationship between DII1and δC、DII2and δC

DII与δC之间的关系如图7所示，图6中两个圆幅值差与δC的关系构成图7，图7中的横虚线是零值线。

由上述分析可知:

1)DII=0。当δC处于图6中两个圆的交点A、B点所对应的角度、图7中曲线与零线的交点E、F 点时，DII=0。解式(18)得δC_cr1=79.2°、δC_cr2=309.6°。满足以上任意一个关系时，突变量选相元件应用条件不变。

2)DII＞0。当δC处于图6中小圆弧上所对应的角度、图7中零值线以上时，DII＞0。由图7可看出79.2° ＜δC＜309.6°，系统Ⅰ的中点电压相角在此范围内适应性良好，突变量选相元件处于良好的应用条件。

3)DII＜0。当δC处于图6中小圆弧上所对应的角度、图7中零值线以下时，DII＜0。由图7可得0 ＜δC＜79.2°，309.6° ＜δC＜360°，突变量选相元件的应用效果受到影响。

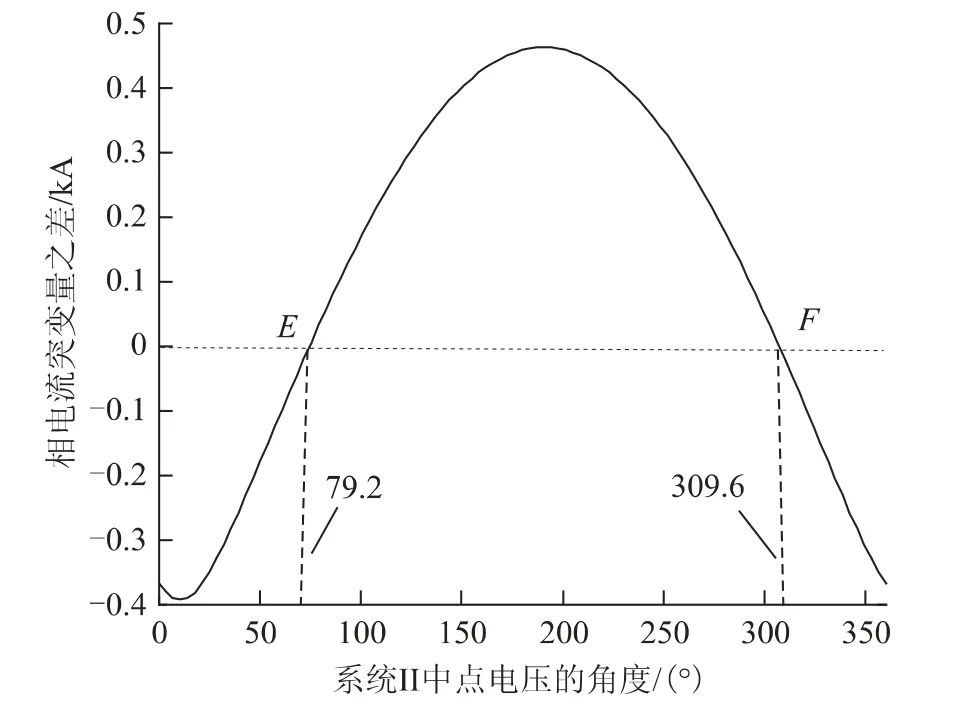
图7 DII与δC之间的关系Fig.7 Diagram of relationship between DIIand δC

4.3 DII大小与系统Ⅱ电源电动势相角关系

1)Ⅱ系统电动势相角满足式(19)或式(20)时，DII=0，适应性基本不变。

2)Ⅱ系统电动势相角满足式(21)时，DII＞0。

3)Ⅱ系统电动势相角满足式(22)时，DII＜0。

5 仿真分析

对上述4.3 节中相电流差突变量之差与Ⅰ的电源电动势相角做仿真。在PSCAD 中建立图4和表1 模型，设置故障发生在中点，系统Ⅱ的电源电动势相角与第4 节中所述一致。

1)临界情况，DII=0。

分别设置式(19)、式(20)中临界点的角度值，则可得仿真故障电流和相电流差突变量值如表2所示。

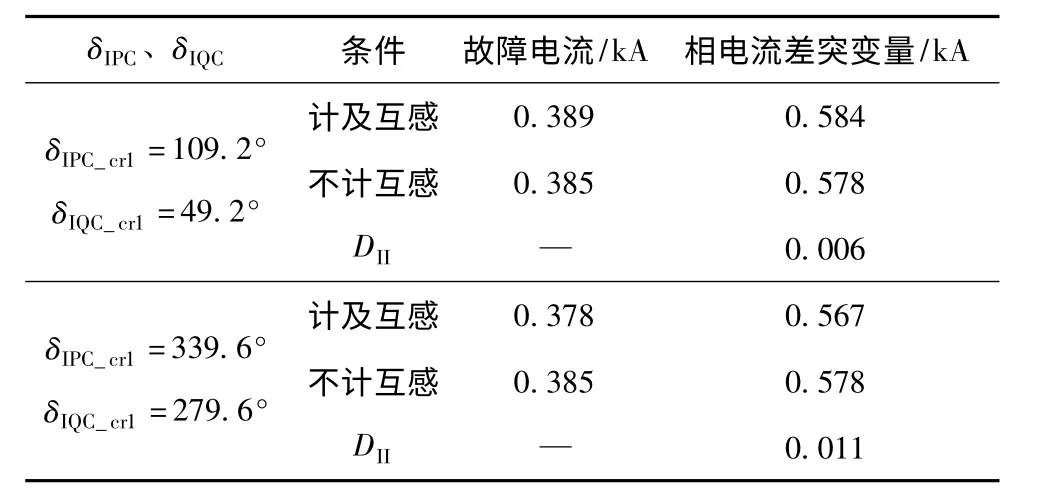
表2 临界情况下系统Ⅱ电源电动势相角与DII关系仿真值Tab.2 The simulated values of the electromotive force phase and DIIin critical situation

临界情况下仿真值和计算结果相比误差很小。

2)DII＞0。

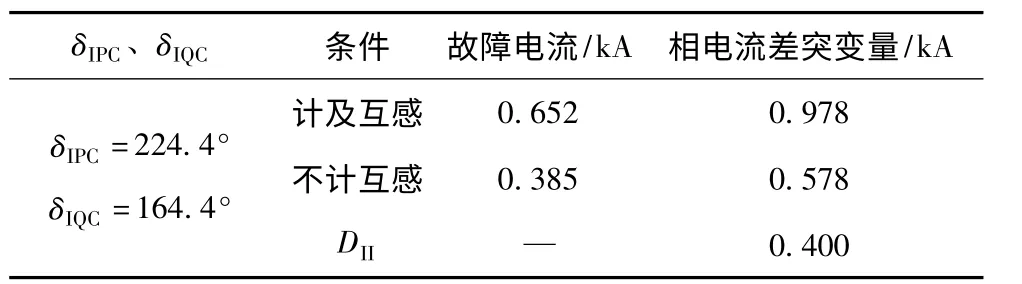
表3 DII＞0时系统Ⅱ电源电动势相角与DII关系仿真Tab.3 The simulated values of the electromotive force phase and DIIin DII＞0

取计算值内的一点仿真证明相电流差突变量大大超过了忽略互感算法时的值。

3)DII＜0。

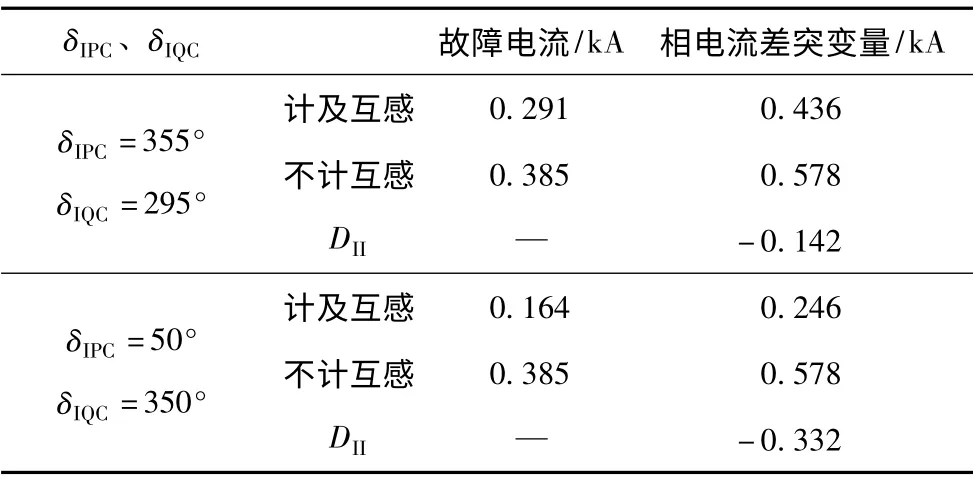
表4 DII＜0时系统Ⅱ电源电动势相角与DII关系仿真Tab.4 The simulated values of the electromotive force phase and DIIin DII＜0

取计算值内的两点仿真证明，当Ⅰ系统的电源电动势角度满足一定的关系时，相电流差突变量远远小于忽略互感算法时的值。

理论分析得到的系统Ⅱ的电源电动势的夹角与相电流差突变量的关系与仿真结果一致，证明理论分析方法是正确的。

6 结论

混压同塔线路使用越来越广泛，跨线故障对安全稳定运行影响巨大，准确的故障选相是保障其健全相继续可靠运行的前提。通过本文分析可知当两系统电源的角度满足一定关系时，相电流差的适应性各不相同。

本文中的方法不仅适用于本文中的故障类型、故障位置和功角差，在上述因素变化时，使用本方法同样可以在相应情况下求出相电流差突变量的适应性。本方法可以对给定系统进行评估，可以准确分析出对相电流差突变量选相的影响大小。以此结论可以预测独立配置不同电压等级系统的选相元件是否合理，为继电保护的规划配置提供坚实的理论依据。

附 录

1 正序阻抗计算过程

正序不计互感，画出不计互感的四回线模型如下。

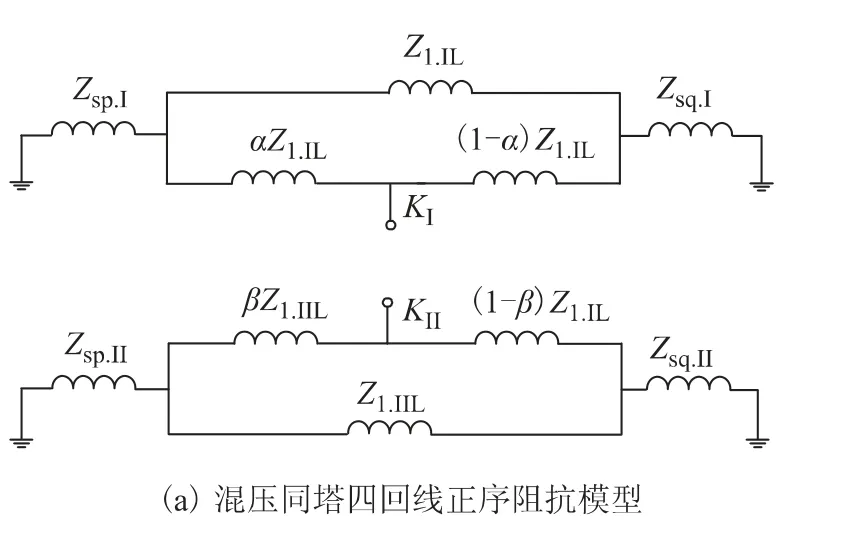
附图1 正序阻抗的归算过程App.Fig.1 Equivalence process of Positive-sequence network

其中

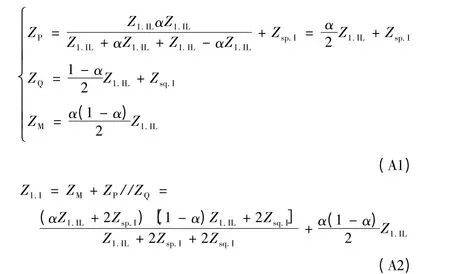
同理可以得到系统Ⅱ和负序网络图的阻抗值。

2 零序阻抗计算过程

附图2中α+β=1;阻抗下标中的sp、sq分别表示电源送端和受端;符号-表示不同回线之间。

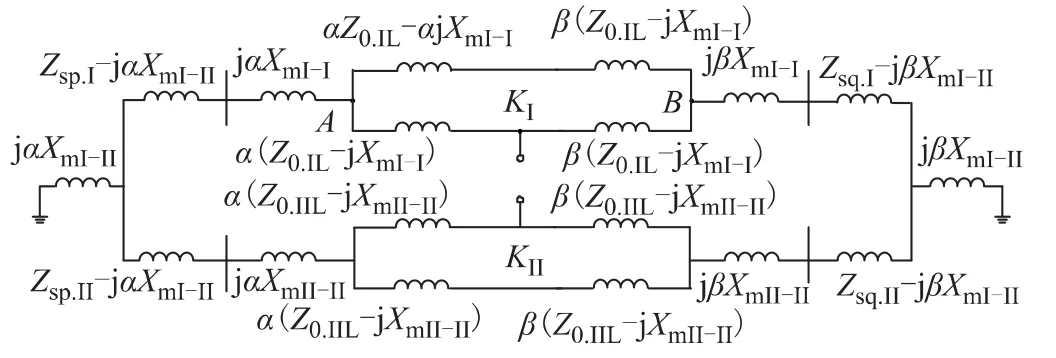
附图2 零序阻抗的去耦电路App.Fig.2 Decoupled zero-sequence impedance network

步骤一:

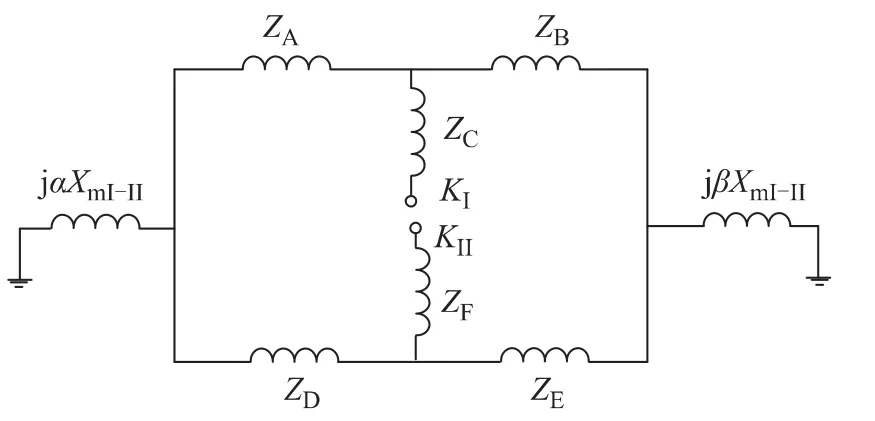
附图3 中间过程1App.Fig.3 Intermediate process1

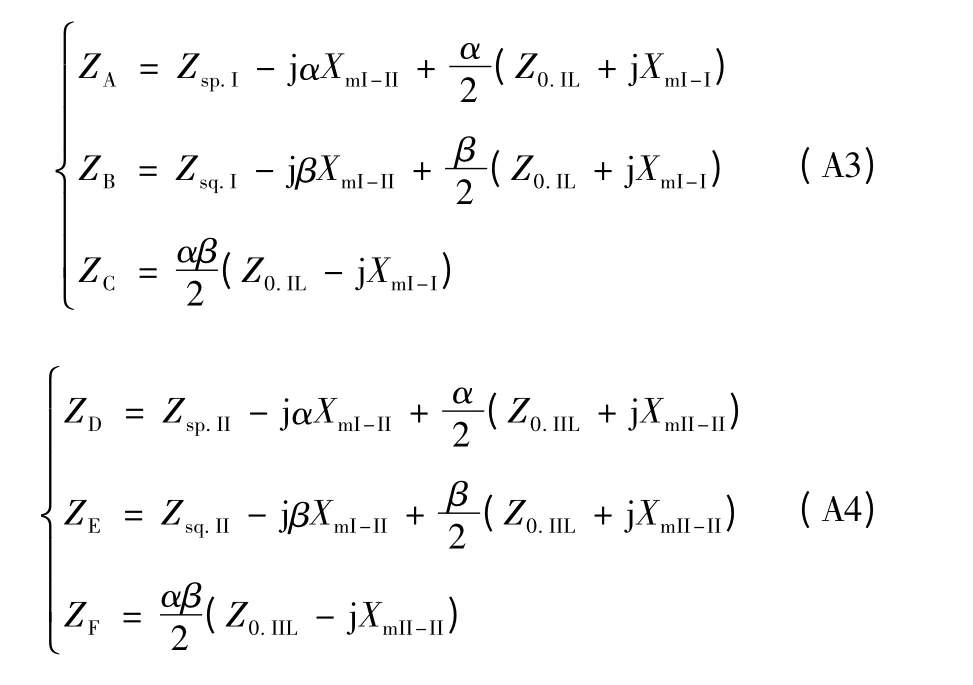
步骤二:

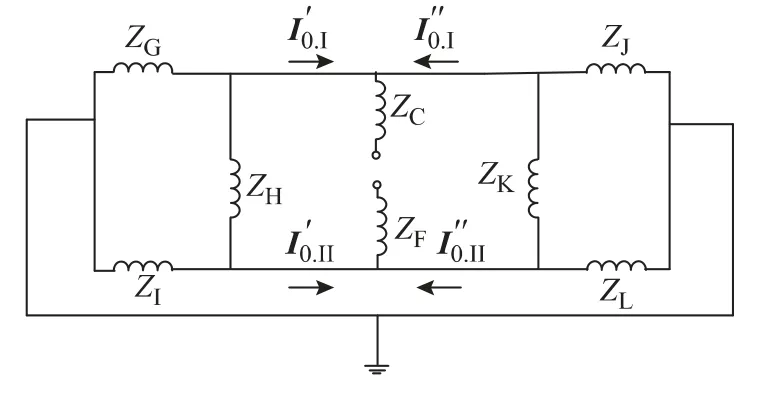
附图4 中间过程2App.Fig.4 Intermediate process2

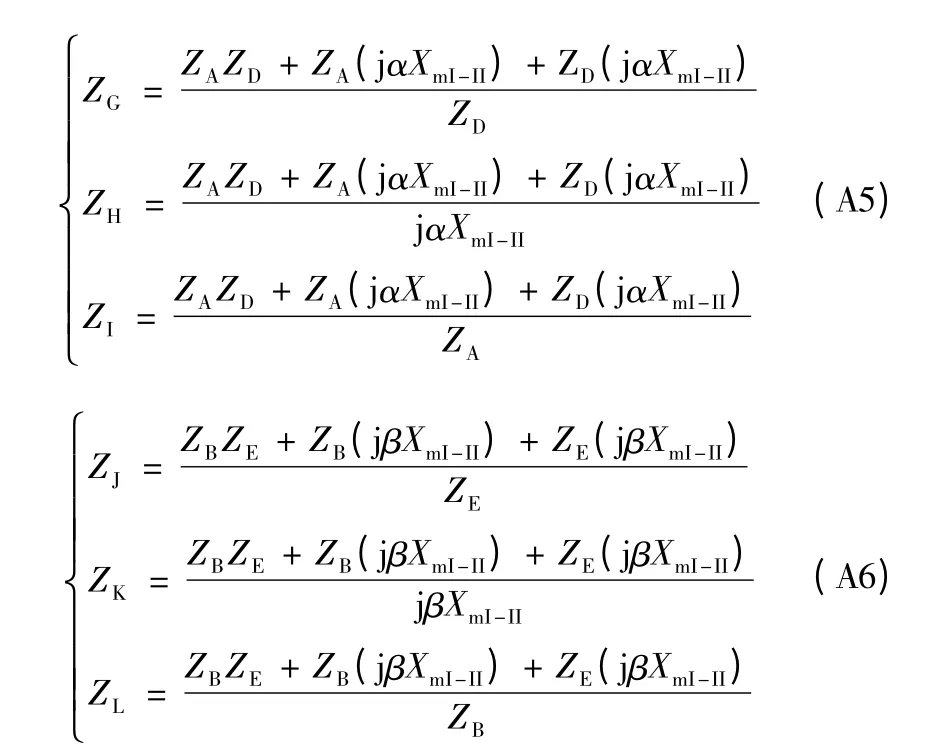
步骤三:

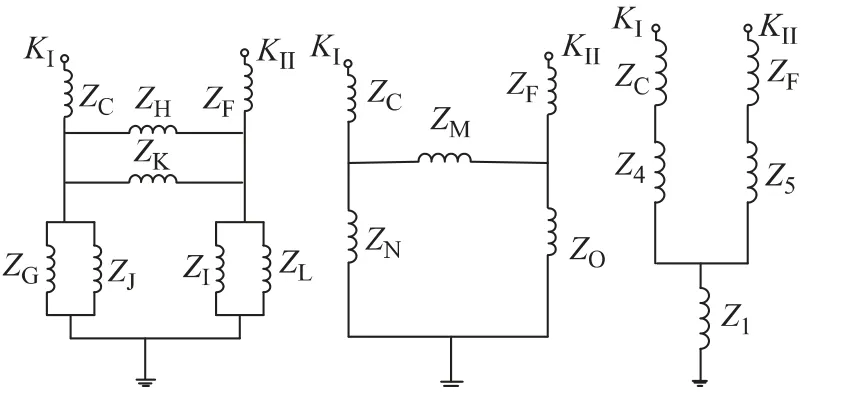
附图5 中间过程3App.Fig.5 Intermediate process3

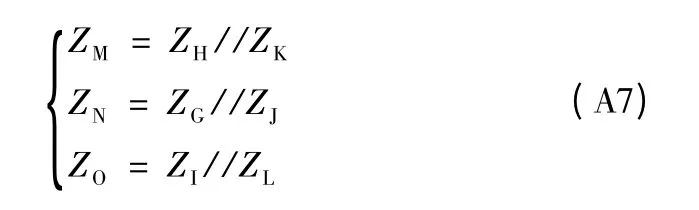
步骤四:

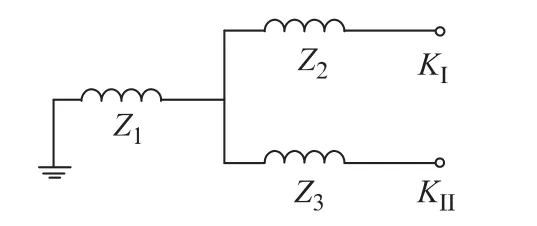
附图6 中间过程4App.Fig.6 Intermediate process 4

步骤较繁琐，在研究过程中编程计算得到归算阻抗。完全附上篇幅太长，但是其归算过程的原理很简单，完全去耦后，经过Y/△变换，串并联过程就可以得到。论文篇幅本身比较长，且重点不在此，所以在论文中只给出了归算原则，并未给出具体过程。

证明式(7)过程如下

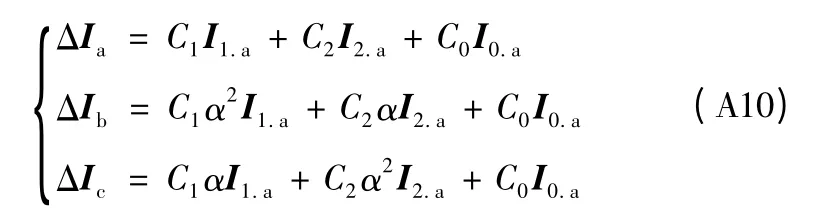
以ΔIab为例推导如下，α=ej120°，则有α2+α+1=0，考虑到C1=C2，I1．a=I2．a=I0．a，

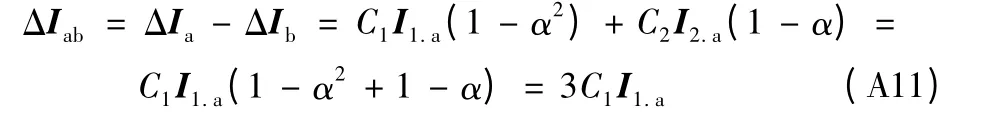
ΔIac、ΔIbc的证明过程类似。

［1］ Stewart J R，Wilson D D．High phase order transmission-a feasibility analysis:part II-over voltages and insulation requirements［J］．IEEE Transactions on Power Apparatus and Systems，1997，35(6):2308-2317．

［2］ 刘家军．平行双回线中串补电容对零序电抗型距离保护的影 响［J］．电工技术学报，2011，26(7):264-270．

Liu Jiajun．Influence of series compensation capacitor on zero-sequence reactance-type distance protection in parallel double-circuit lines［J］．Transactions of China Electrotechnical Society，2011，26(7):264-270．

［3］ 李斌．特高压同杆双回线的环流不平衡及其影响［J］．电工技术学报，2012，27(4):202-208．

Li Bin．Circulating unbalanced current and its influenceof double-circuit UHV transmission lines［J］．Transactions of China Electrotechnical Society，2012，27(4):202-208．

［4］ 陈福锋，钱国明．基于同杆双回线跨线故障识别的选相方案［J］．电力系统自动化，2008，32(6):66-70．

Chen Fufeng，Qian Guoming．Research on fault phase selector of protective relay for double circuit lines based on crossing-line fault identifying［J］．Automation of Electric Power Systems，2008，32(6):66-70．

［5］ 俞波，杨奇逊，李营，等．同杆并架双回线保护选相元件研究［J］．中国电机工程学报，2003，23(4):38-42．

Yu Bo，Yang Qixun，Li Ying，et al．Research on fault phase selector of protective relay for double circuit lines on the same tower［J］．Proceedings of the CSEE，2003，23(4):38-42．

［6］ 张海，黄少锋．利用电压辅助电流选相的同杆双回线单端电气量选相原理［J］．中国电机工程学报，2013，33(7):139-148．

Zhang Hai，Huang Shaofeng．A fault phase selection scheme of currents with assistant voltages for commontower double-circuit transmission lines using one-terminal electrical quantities［J］．Proceedings of the CSEE，2013，33(7):139-148．

［7］ 李振兴．基于综合阻抗比较原理的广域继电保护算法［J］．电工技术学报，2012，27(8):179-186．

Li Zhenxing．A study of wide-area protection algorithm based on integrated impedance comparison［J］．Transactions of China Electrotechnical Society，2012，27(8):179-186．

［8］ 李伟，毕天姝，徐振宇，等．相间接地故障时常规选相元件动作行为分析及改进措施［J］．电力系统保护与控制，2012，40(3):67-72．

Li Wei，Bi Tianshu，Xu Zhenyu，et al．Analysis of phase selector action and improving scheme for twophase-to-ground fault［J］．Power System Protection and Control，2012，40(3):67-72．

［9］ 田书，刘芳芳，任晓明．基于暂态量的同塔双回线路故障选相研究［J］．电力系统保护与控制，2015，43(1):50-54．

Tian Shu，Liu Fangfang，Ren Xiaoming．Research on transient-based faulty phase selection for double-circuit lines on the same tower［J］．Power System Protection and Control，2015，43(1):50-54．

［10］ 曾耿晖，黄明辉，刘之尧，等．同杆线路纵联零序保护误动分析及措施［J］．电力系统自动化，2006，30(20):103-107．

Zeng Genghui，Huang Minghui，Liu Zhiyao，et al．Analysis on mis-operations of zero-sequence protective relay in double circuit lines on the same tower［J］．Automation of Electric Power System，2006，30(20):103-107．

［11］ 张琦兵，邰能灵，袁成，等．同塔四回输电线的相模变换［J］．中国电机工程学报，2009，29(34):57-62．

Zhang Qibing，Tai Nengling，Yuan Cheng，et al．Phase-mode transformation of four-parallel lines on the same tower［J］．Proceedings of the CSEE，2009，29(34):57-62．

［12］ 刘玲，范春菊．基于六序分量法的跨电压等级的同塔四回线的故障计算［J］．电力系统保护与控制，2010，38(9):6-11．

Liu Ling，Fan Chunju．Fault calculation for joint four transmission lines of different voltage grades on the same tower based on six-sequence-component method［J］．Power System Protection and Control，2010，38(9):6-11．

［13］ 胡志坚，姜美玲．不同电压等级同塔四回输电线路零序电流补偿系数整定研究［J］．电网技术，2012，35(7):60-66．

Hu Zhijian，Jiang Meiling．Setting of zero sequence current compensation coefficient for four-circuit transmission lines in different voltage classes on same tower［J］．Power System Technology，2012，35(7):60-66．

［14］ 周春霞，余越，赵寒，等．特高压同塔双回线路零序电流补偿系数整定对接地距离保护的影响研究［J］．电网技术，2012，36(12):106-111．

Zhou Chunxia，Yu Yue，Zhao Han，et al．Influence of zero-sequence current compensation coefficient setting on earth-fault distance protection for double circuit uhvac transmission lines on the same tower［J］．Power System Technology，2012，36(12):106-111．

［15］ 马静，史宇欣，马伟，等．基于分布参数的同杆双回线跨线及接地故障单端定位方法［J］．电网技术，2014，36(9):2525-2531．

Ma Jing，Shi Yuxin，Ma Wei，et al．Distributed parameter based one-end fault location for inter-line fault and earth fault in double-circuit transmission lines on same tower［J］．Power System Technology，2014，36(9):2525-2531．