增强型滑动平均滤波算法及其在畸变电网相位同步控制中的应用

熊连松 卓 放 刘小康

(电力设备电气绝缘国家重点实验室(西安交通大学)西安 710049)

0 引言

非线性设备与负荷的大量投运，使得电网中不可避免地存在着谐波污染。当电网严重畸变时，相位同步控制无法获得准确而稳定的电网同步相位信息，从而削弱了并网变流器的安全稳定性。因此，在电网波形严重畸变的情况下如何进行快速准确的相位同步是并网逆变器控制的关键技术［1-4］。

现有的锁相方法多在同步旋转坐标系下实现。其基本思路为［3-6］:将静止abc 坐标系下的正弦量变换成同步旋转dq 坐标系下的直流量，并将q 轴分量输入到PI 调节器，通过控制q 轴分量为0 即可实现相位锁定［3］。然而，当电网波形畸变时，abc 坐标系下的波形不再是标准的正弦波，同步旋转坐标系下的q 轴分量也不再是恒定不变的直流量，而是包含了谐波成分的非标准直流量。此时，若继续控制q 轴分量为0，则锁相器将输出振荡的相位波形［4-6］。此时，通过提取q 轴分量中的直流成分，并将其送入PI 调节器进行闭环控制，即可获得稳定且无稳态误差的相位波形。

现有的谐波影响抑制方法多以使用低通滤波器(Low-Pass Filter，LPF)为主［3-7］，但LPF 的设计需同时考虑两方面的矛盾因素［5］:一是需要较大的带宽以提高动态响应速度，确保电网电压突变时能够获得可接受的动态响应性能;而另一方面需降低带宽以使谐波充分地衰减，以尽可能减小输出相位的稳态误差，尤其是低频次、高含量谐波的影响。然而，实际应用中很难做出一个理想的折中方案。此外，LPF 仅能在一定程度上对谐波影响进行抑制，而无法从理论上实现谐波影响的完全消除。

若充分利用谐波波形的周期性与半波对称性，则可实现谐波的完全滤除［8-19］。类似的方法主要有:滑动平均滤波法(Moving Average Filter，MAF)［8-11］、信号延时对消法(Delayed Signal Cancellation，DSC)［12］及其衍生方法［13-18］。为了提高不对称电网相位同步的准确度，文献［5］提出了信号延时1/4 周期对消法，从而有效解决了dq 坐标系下的二倍频波动问题。将该思想进行推广，即可得到滤除任意特定次谐波的通用DSC 算法［12］;此外，若干个串联的DSC(Cascaded DSC，CDSC)可同时滤除多个不同频次的谐波［13，14］。DSC 算法优异的谐波滤除能力以及设计上的灵活性，使其在谐波检测［14］、同步相位控制［15，16］、异常电压穿越［17］以及电能质量治理［18］等诸多领域都获得了成功的应用。然而，DSC 算法也有一些难以克服的缺陷，例如:①无法抑制高频随机噪声的干扰，采用DSC 算法滤波时必须额外增加LPF 以滤除随机噪声;②同时滤除多个谐波时，必须将多个DSC 模块进行串联［19］，此时需要大量的数据存储和数学运算，因此CDSC 算法显著增加了控制器的负担［15］;③DSC 算法的准确性受限于采样频率以及待滤除谐波的次数［19］，采样率越低，谐波次数越高，则DSC 算法的误差越大［13］，而高性能变流器控制中的高次谐波影响却不容忽视。

MAF 算法则可有效避免上述问题，且能几乎完全地滤除电网电压信号中的谐波，因此逐渐获得了大量的关注和应用。MAF 算法常用于滤除高频随机噪声，对周期性干扰信号的抑制尤其有效［8］。若将谐波视为周期性的噪声信号，则可使用MAF 算法来滤除谐波信号［8-11］。由于谐波具有确定的周期，因此可将谐波周期作为MAF 算法的滑动长度，以完全地滤除该特定次谐波。显然，谐波的次数不同，则MAF 算法的滑动长度也不同。当需要同时滤除一组指定次数的谐波时，现有文献尚未给出MAF 算法滑动长度的设计方法。

本文对MAF 算法滑动长度的优化设计问题进行了深入研究，得到了同时滤除若干指定次谐波时MAF 滑动长度应满足的充要条件，并据此提出了增强型MAF(Enhanced MAF，EMAF)算法以及基于EMAF 的畸变电网快速开环锁相方法。此外，从响应时间、数据存储量、暂态振荡幅度、谐波滤除能力以及随机噪声抑制能力等方面深入地对比分析了CDSC 算法与EMAF算法的技术经济性。最后，通过各种工况下的实验证明了分析结论的正确性以及改进方法的先进性。

1 滑动平均滤波法MAF 的原理与模型

1.1 MAF 滤除单次谐波

MAF 是一种极为有效的抑制周期性干扰的方法，其在连续域下的表达式为［8］

式中:h(·)为含有周期性干扰的信号;Th为MAF 的滑动长度。

因此，MAF 的传递函数为

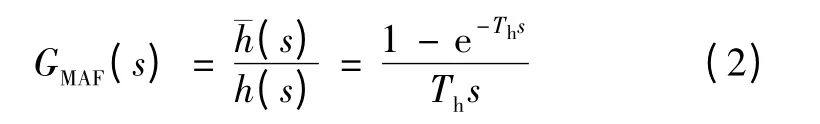
据此可知，MAF 的响应时间与其滑动长度Th相等，滑动长度越大，则MAF 的动态响应时间越长。

将式(2)中的s 替换为jω，则可得MAF 的幅频表达式为

分析MAF 的幅频特性可知:当ω 为0时，MAF的增益为1，即MAF 对直流信号无衰减;而当ω 为2πn/Th(n=1，2，3，…)时，MAF 的增益为0;当ω为其他值时，MAF 的增益小于1，且随着ω 的增大而迅速降低。MAF 的这一特性与LPF 类似，且能实现对特定频率信号的完全滤除。显然，若将MAF 的滑动长度Th设置为电网的工频周期T，则MAF 增益为0 的ω即为电网的谐波频率。因此，充分利用这一特性，即可实现对电网谐波的完全滤除。

根据上述分析可知，对于n 次谐波而言，连续域下MAF 的表达式应修改为

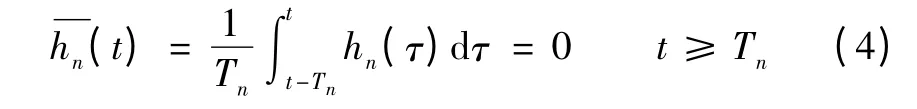
式中Tn为n 次谐波的谐波周期，也即MAF 的滑动长度。为阐述方便，将用于滤除n 次谐波的MAF 记为MAFn。

因此，对于n 次谐波而言，MAFn 的延时时间为一个谐波周期［16］，即Tn。在MAFn 的暂态过程内，谐波成分被显著地抑制了;到达稳态后，谐波则被MAFn 完全地滤除了(MAFn 的增益为0)。

MAF 算法在实际控制系统中使用时，需要将其转换为离散表达式。因此，MAF 的离散表达式为

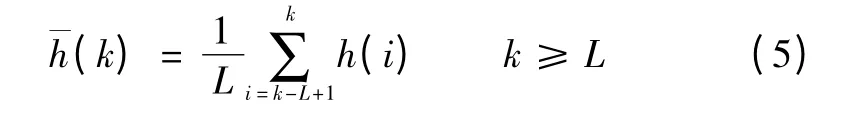
式中L 为MAF 的滑动长度。

为了减小嵌入式控制器的计算负担，MAF 算法常采用式(6)等效实现，即

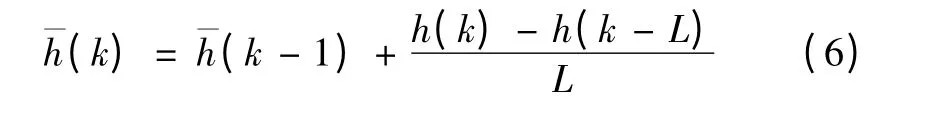
假设采样时间为Ts，且Ts≪Tn。则式(4)所示的MAFn 的离散表达式为

式中Ln为MAFn 的滑动长度，且

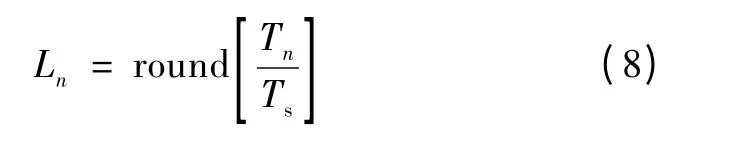
式中round［·］为最近取整运算符号。

式(7)的结果也可从谐波波形的几何意义上进行解释，如图1所示。谐波在一个周期内是正负半周对称的，因此一个谐波周期内的所有采样值总是正负相消的，其和始终为0。这也是MAF 能够实现谐波完全滤除的原因。

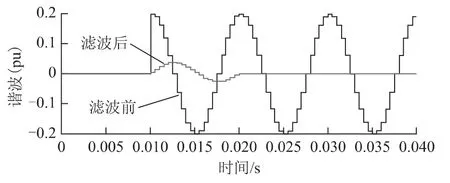
图1 MAF 滤除单次谐波的示意图Fig.1 MAF to eliminate a specific harmonic

1.2 MAF 同时滤除多次谐波

若需要同时滤除若干次谐波时，可通过若干个MAFn 的串联来实现，即级联式MAF(Cascaded MAF，CMAF)。因此，类似于CDSC 算法，CMAF 在设计上具有较好的灵活性，可实现对若干指定次谐波的完全滤除，对于已知谐波分布规律或特定次谐波提取等应用场合有较大的使用价值。此时，CMAF 的响应时间TCMAF为各独立MAFn 响应时间Tn之和。

若同时滤除N 次以内的所有任意次谐波，此时

由式(9)可知，待滤除的谐波成分越多，CMAF的响应时间就越长;当N 趋于无穷大时，则延时时间也趋于无穷大。显然，如此长时间的延时以及如此大量的数据存储是实际应用中无法接受的。因此，CMAF 仅用于滤除有限个数谐波的场合。当同时滤除多个谐波时，一般利用式(5)进行计算，且此时MAF的滑动长度L 应为

将MAF 的滑动周期设置为电网工频周期T时，MAF 可同时滤除任意次的谐波，且响应时间为一个工频周期T。同时滤除一组指定次谐波时，若CMAF 的响应时间小于T，则优先采用CMAF 算法，否则采用滑动周期为T 的MAF 算法，如此即可将谐波滤除算法的响应时间始终限制在一个工频周期内。

研究表明，同时滤除多个指定次谐波时，上述方法依然无法实现响应时间上的最优化，动态响应性能仍无法与CDSC 算法相媲美。为此，下文针对同时滤除多个指定次谐波这一问题，提出了优化的MAF 算法及其滑动长度的优化设计方法。

2 增强型滑动平均滤波EMAF 算法

2.1 EMAF 算法的原理

将n 次谐波的滑动长度扩大Zn(Zn=1，2，3，…)倍，则式(7)可转换为

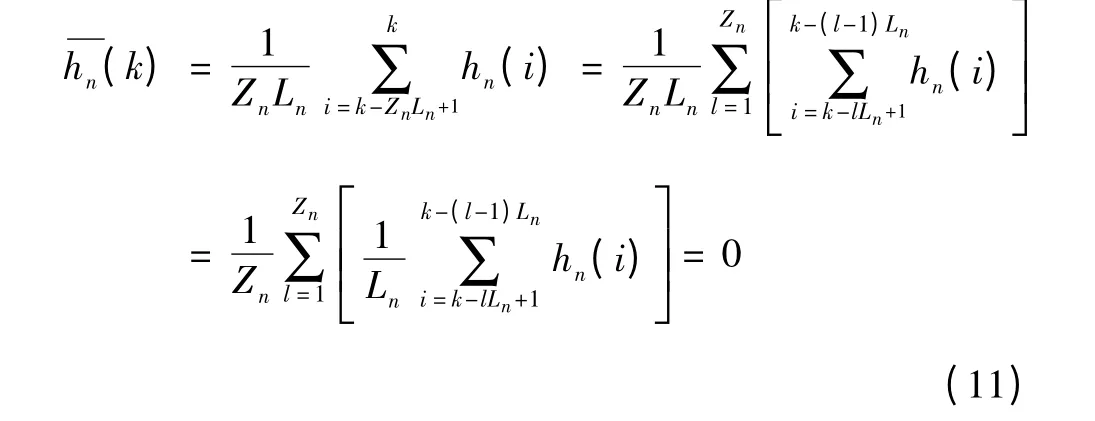
式中k≥ZnLn。

由式(11)可知，只有当MAFn 的滑动长度取n 次谐波一个周期内采样点数Ln的整数倍(即ZnLn)时才能实现n 次谐波的完全滤除;同时，MAFn 的暂态响应时间也因此扩大为ZnLn。

因此，通过设计合适的滑动长度，即可实现仅使用一个MAF 模块就一次性滤除任意指定次谐波，且该MAF 的滑动长度与谐波的周期有着紧密的关系，这也是区别于高频随机噪声滤波以及CMAF 的主要特点。因此，将具备此功能的MAF 定义为增强型滑动平均滤波器(Enhanced MAF，EMAF)。

根据式(11)及其结论可得到快速滤除任意次谐波的EMAF 方法及其滑动长度。若EMAF 具备同时滤除任意指定次谐波的能力，则EMAF 的滑动长度LEMAF必须满足的充要条件为

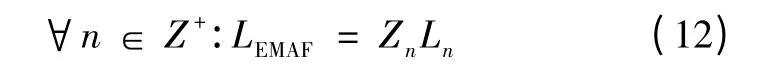
由此可知，满足式(12)的LEMAF必然是各MAFn 滑动长度Ln的公倍数。显然，EMAF 的响应时间TEMAF也有类似规律，且可描述为

式(12)、式(13)所示的充要条件也容易从谐波波形的几何特征上予以解释。若某次谐波能被EMAF 完全地滤除，则EMAF 的滑动周期TEMAF必然恰好完全地包含了若干个整谐波周期;反之，能被一个EMAF 滑动周期TEMAF恰好完整地覆盖若干个整谐波周期的谐波一定能被EMAF 完全地滤除。由于谐波频率是基波频率的整数倍，因此滑动周期为电网工频周期的MAF 必然能同时完全地覆盖各次谐波的若干个整谐波周期，这就解释了现有MAF 滑动周期为一个电网工频周期的原因［9］。

图2用5 种谐波举例说明了EMAF 的充要条件。其中，谐波1 的8 个整周期被滑动周期TEMAF完全地覆盖，因此谐波1 可被EMAF 完全地滤除;同理，滑动周期TEMAF分别完全地覆盖了谐波3 的3 个整周期以及谐波5 的1 个整周期，因此谐波3、5 也可被EMAF 完全地滤除。然而，谐波2、4 却未能在滑动周期TEMAF内完全地正负相消(箭头所示的空白区域即为未被抵消的部分)，故而无法被EMAF 完全地滤除。

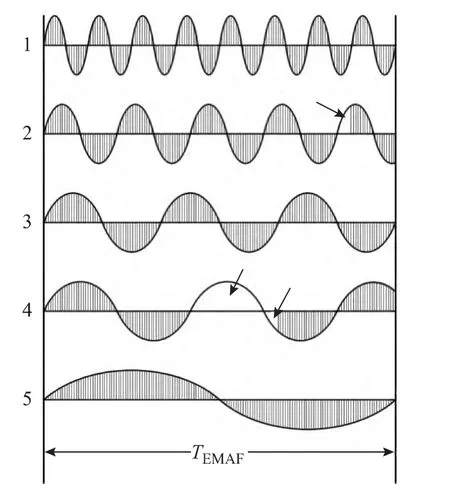
图2 EMAF 同时滤除一组指定次谐波的示意图Fig.2 EMAF to eliminate harmonics with specific orders

此外，满足充要条件且响应时间TEMAF最短的EMAF 的滑动长度LEMAF必然是各MAFn 滑动长度Ln及响应时间Tn的最小公倍数。为了提高EMAF 的响应速度，TEMAF、LEMAF均是指满足充要条件的最短响应时间及最小滑动长度。

显然，滤除一组有限个特定次谐波时，EMAF 仍然不一定是时间最优的。因此，选择EMAF 还是CMAF，取决于二者的响应时间。一般选择二者中暂态响应较快的。例如:

1)同时滤除5、7 次谐波时，TEMAF为基波周期T，而TCMAF为12T/35，因此选择CMAF。

2)同时滤除2、4、6 次谐波时，TEMAF为T/2，而TCMAF为11T/12，因此选择EMAF。

3)同时滤除3、6、9、12 次谐波时，TEMAF为T/3，而TCMAF为25T/36，因此选择EMAF;依次类推。

总之，待滤除的谐波成分越多，谐波的次数越低，则EMAF 的响应速度优势越明显;反之成立。

2.2 EMAF 算法的响应时间规律

由于EMAF 的响应时间与其滑动周期相等，而EMAF 的滑动周期满足式(13)所示的充要条件。因此，EMAF 的响应时间由待滤除谐波的次数决定。通过对EMAF、CDSC 滤除任意次谐波所需时间及数据存储量的统计，可得出如下重要规律:

1)同时滤除所有任意次的偶次谐波。此时，TEMAF、TCDSC均为T/2。在数据存储量以及加法、乘法运算次数方面，EMAF 的数据存储量(即LEMAF)以及运算次数均有限;而CDSC 则需要无穷个DSC 模块串联，其数据存储量以及运算次数皆趋于无穷。为了使CDSC 方法能在嵌入式控制器中使用，改进的方法是采用CDSC 来滤除低次谐波，而用LPF 滤除高次谐波［15］。即便如此，CDSC 算法的数据存储量及运算次数均依然远大于EMAF 算法。

2)同时滤除所有任意次的奇次谐波。此时，TEMAF、TCDSC分别为T、T/2。此时，CDSC 算法的响应速度明显优于EMAF 算法。在数据存储量以及加法、乘法运算次数方面，EMAF 的数据存储量为CDSC 的两倍，而两者的运算次数基本相当。

3)同时滤除所有任意次的谐波。此时，TEMAF、TCDSC均为T。在数据存储量以及运算次数方面，EMAF的数据存储量与运算次数均有限;而CDSC 算法则几乎为上述两种情况的总和，且远大于EMAF 算法。此时，EMAF 算法的综合性能明显优于CDSC 算法。

此外，需补充说明的是:电网中的谐波多以奇次为主，且现有的并网变流器控制大多在同步旋转坐标系下进行。因此并网变流器控制通常需要处理的谐波以偶次为主，即规律1)。此时，EMAF 算法的比较优势更明显。

2.3 EMAF 算法的谐波衰减性能

由式(5)可知，MAF 及EMAF 是在一个滑动周期内对所有的采样值进行平均化;而DSC 算法仅对两个特定时刻的采样值求平均。因此，DSC 方法在暂态过程中仅能将谐波幅值降低50%。当有DSC 无法滤除的谐波存在时，该谐波经过DSC 运算后幅值仅能衰减0.707 倍，从而未能实现对该次谐波的有效抑制。而EMAF 则可使各次谐波的幅值显著降低，且采样频率越高，滑动周期越长，则暂态过程中的谐波幅值衰减越明显。在较高的采样频率以及较大的滑动长度下，EMAF 能使谐波幅值趋于0，几乎完全地滤除谐波的影响。因此，在谐波滤除算法到达稳态前，EMAF 对谐波的抑制能力明显强于DSC。

以图3为例，输入2 次、3 次谐波各0.2(pu)，采样频率为10 kHz。MAF、DSC 的滑动长度分别为100、50，且分别于10 ms、5 ms 进入稳态;暂态过程中，MAF 对谐波的衰减度明显大于DSC;稳态时，二者均完全地滤除了2 次谐波;同时，MAF 使3 次谐波的幅值降低到0.04(pu)，而DSC 仅使3 次谐波的幅值降低到原来的0.707 倍，即0.141(pu)。

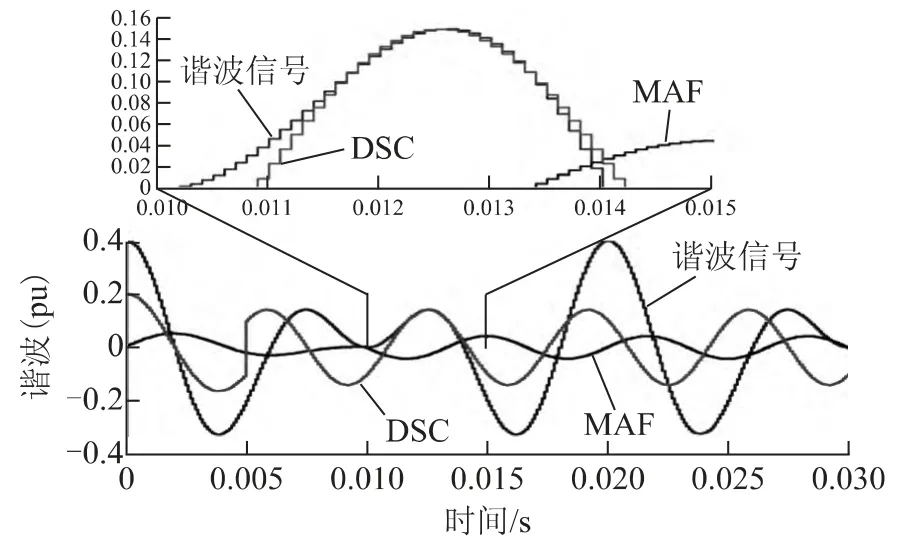
图3 MAF、DSC 的暂态谐波衰减性能Fig.3 Harmonics attenuation performance in the transient of MAF and DSC

此外，EMAF 与DSC 的稳态谐波滤除性能也有较大差别。理论上，当Ts≪Tn时，EMAF 与CDSC 均能完全地滤除谐波。而在数字控制中，受采样频率与取整运算的限制，采样时刻只能在允许的条件下趋近于理论时刻。因此，EMAF 与CDSC 无法实现绝对的完全滤除谐波，且当谐波的次数越大时，一个谐波周期内的采样点数量就越少，谐波完全滤除程度就越弱。CDSC 方法将两个特定时间点上的采样值进行抵消，因此抵消的程度十分依赖于采样时刻以及采样准确度。而EMAF 则可将上述误差在整个滑动区域内进行分散。因此，稳态时EMAF 的谐波完全滤除能力明显强于CDSC 方法，且谐波次数越高，采样频率越低，则优势越明显。

谐波完全抑制性能的影响规律如图4所示。其中，图4a 中的谐波次数为3，采样频率为5 kHz;图4b 中的谐波次数为7，采样频率为2.5 kHz。两种工况下，EMAF 均能完全地滤除谐波;而CDSC 则有一定的稳态误差，且谐波次数越高，采样频率越低时，稳态误差越大。

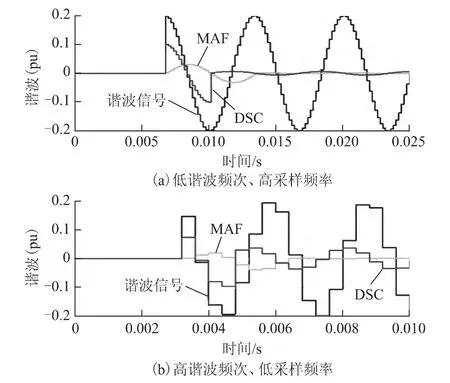
图4 MAF、DSC 的稳态谐波衰减性能Fig.4 Harmonics attenuation performance in steady state of MAF and DSC

2.4 EMAF 算法的噪声衰减性能

由于EMAF 算法能够将高频随机噪声在其整个滑动区域内进行平均化，因此能显著抑制高频随机噪声。而CDSC 算法仅在两个特定的时间点上对随机噪声进行平均化，即不具备对噪声的“记忆”能力，因此无法有效滤除高频随机噪声的影响，甚至在部分情况下还会放大噪声，如图5所示。到达稳态后，MAF算法的输出几乎为0，而DSC 算法的输出则包含了大量随机噪声，在部分采样时刻还导致高频噪声的幅值放大了。

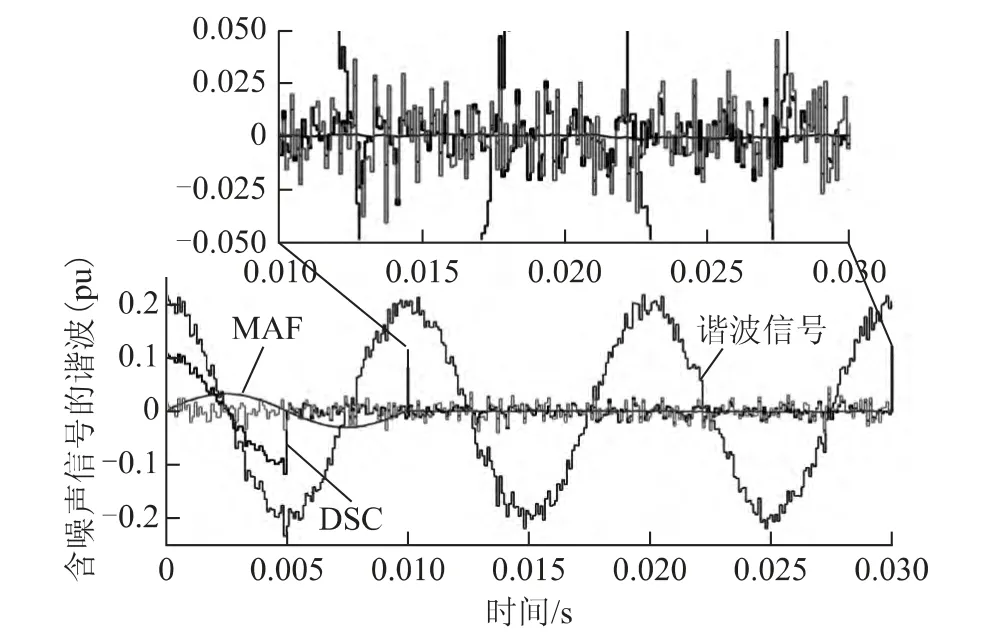
图5 MAF、DSC 的噪声衰减性能Fig.5 Noise attenuation performance of MAF and DSC

由此可知，使用CDSC 方法滤除谐波时还必须额外配置专门的LPF 以滤除高频随机噪声，而EMAF 算法则无需额外设置LPF。

3 基于EMAF 算法的畸变电网快速开环锁相方法

利用文献［10，20］中提出的快速开环锁相原理，提出了基于EMAF 算法的畸变电网快速开环锁相方法，以验证EMAF 算法在畸变电网锁相应用中的有效性和先进性。

当计及谐波的影响时，三相电网电压可描述为

式中:Um、θ、ω分别为电网电压的幅值、初始相位、频率;n、Umn、φn分别为谐波次数、n 次谐波的幅值

将式(14)进行同步旋转变换可得

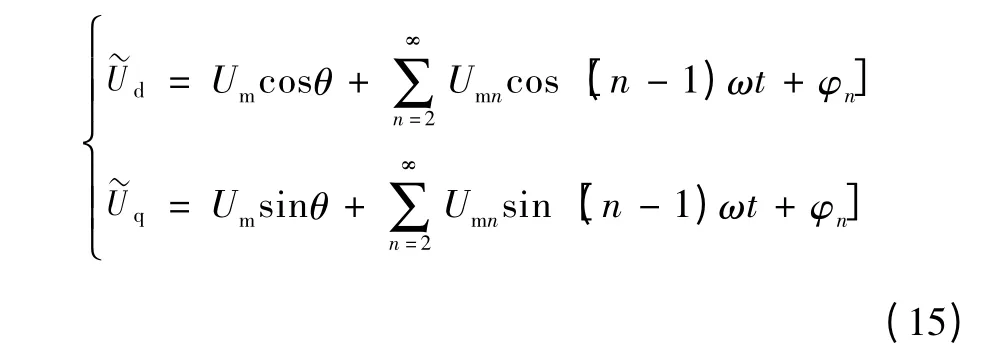
其中，同步旋转变换矩阵为

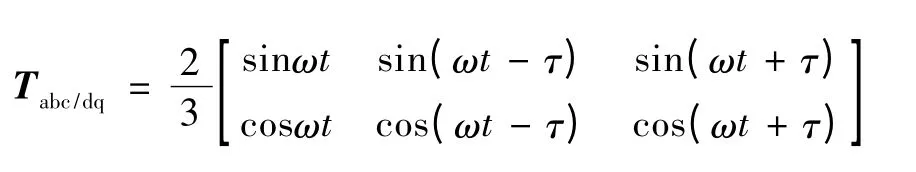
利用EMAF 算法即可完全地滤除Ud和Uq中的谐波分量，如图6所示。因此，三相畸变电压中基波分量在旋转坐标系下的表达式为

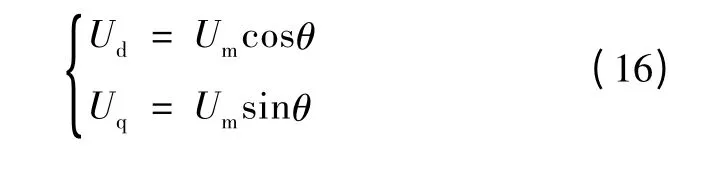
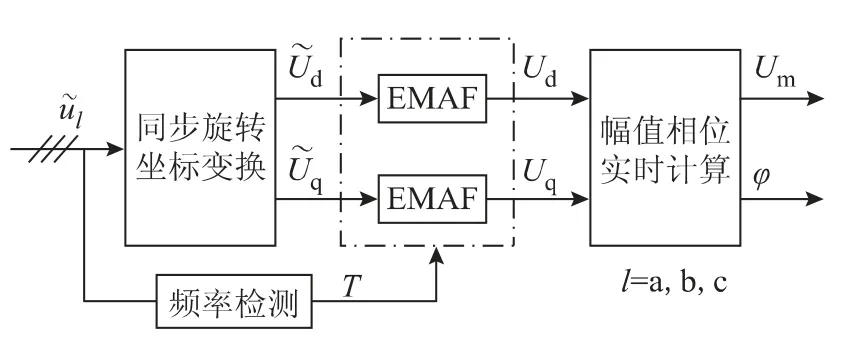
图6 基于EMAF 算法的快速开环锁相方法Fig.6 EMAF based open-loop phase locking scheme

因此，由式(16)即可直接计算出电网电压基波分量的幅值以及实时同步相位［10］，即

式中

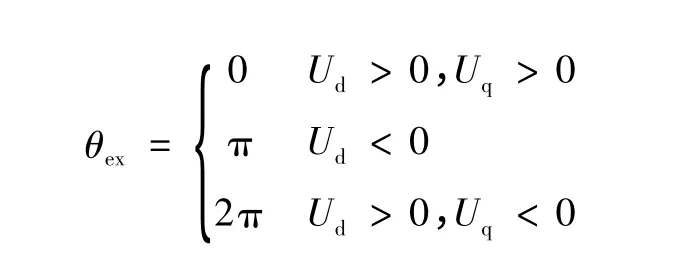
式(18)即为快速开环相位计算的公式，据此即可得到基于EMAF 算法的畸变电网快速开环锁相方法，如图6所示。

此外，当考虑电网电压不对称时，其负序、零序分量经过旋转坐标变换后依然为各次谐波(也可能会出现工频分量)的组合［12-18］，因此也能通过EMAF 算法实现基波正序分量的快速准确提取。当考虑电网频率变化时，通过引入频率检测算法即可实现频率自适应［10］。例如，利用简单易行的过零检测法即可捕获电网频率，其延时时间约为0.5～1 个工频周期。当需要考虑多个过零点问题时，可采用其他更加准确也更加复杂的频率检测方法［15］。将实时检测出的电网频率代入式(8)及式(12)后即可实现对EMAF 算法滑动长度的实时调节，从而有效解决频飘导致的稳态误差。

4 实验验证

实验使用TMS320F28335 型DSP 作为核心控制器，并采用CCS3.3 软件实现了实验算法的软件开发和验证。实验信号由另一套完全相同的DSP 控制器模拟，且采样频率为10 kHz。为了便于观察实验结果，控制器外加了D-A 转换器将模拟的电网电压信号、实时计算的相位信息转换为模拟量输出。示波器型号为Tektronix DPO3034。

实验共设置了6 种场景，第1 种场景对比了EMAF、CMAF、MAF 在处理多谐波时的动态响应速度，证明了EMAF 算法的快速性;第2、3、4 种场景比较了EMAF 与CDSC 的技术特点及其在畸变电网开环锁相中的技术性能。第5、6 种场景则分别验证了EMAF 在频率漂移及三相不对称时的有效性。此外，由于能够直接采集到的是三相静止坐标系下的信号，因此实验部分所述的谐波次数均是相对于静止坐标系。但谐波滤除算法均在旋转坐标系下实现。因此，静止坐标系下的奇、偶次谐波分别对应旋转坐标系下的偶、奇次谐波。

4.1 实验场景1:EMAF、CMAF 与MAF 同时消

除多个谐波分量时的响应时间对比

图7分别为EMAF、CMAF、MAF 算法同时滤除3、5 次谐波时的实验结果。由图可知，3 种谐波消除算法均能有效抑制谐波成分导致的锁相稳态误差，但其动态响应时间却有较大差别，分别为10 ms、15 ms、20 ms。因此，同时处理多个谐波成分时，EMAF 算法在动态响应速度上优势明显。

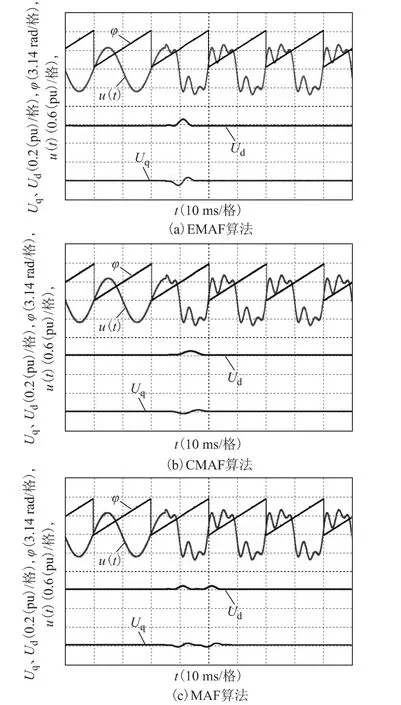
图7 EMAF、CMAF、MAF 的对比Fig.7 Comparison of EMAF，CMAF and MAF

4.2 实验场景2:滤除偶数次谐波

图8分别为EMAF、CDSC、CMAF、MAF 算法同时滤除2、4 次谐波时q 轴电压的输出波形，其响应时间分别为20 ms、10 ms、26 ms、20 ms;图9为同时滤除2、4、6、8 次谐波时的结果，其响应时间分别为20 ms、10 ms、33 ms、20 ms，均与理论分析结果一致。

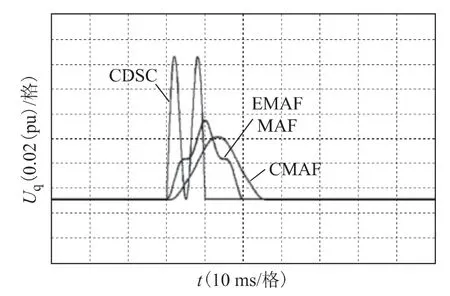
图8 滤除2、4 次谐波Fig.8 Eliminate the 2ndand 4thharmonics

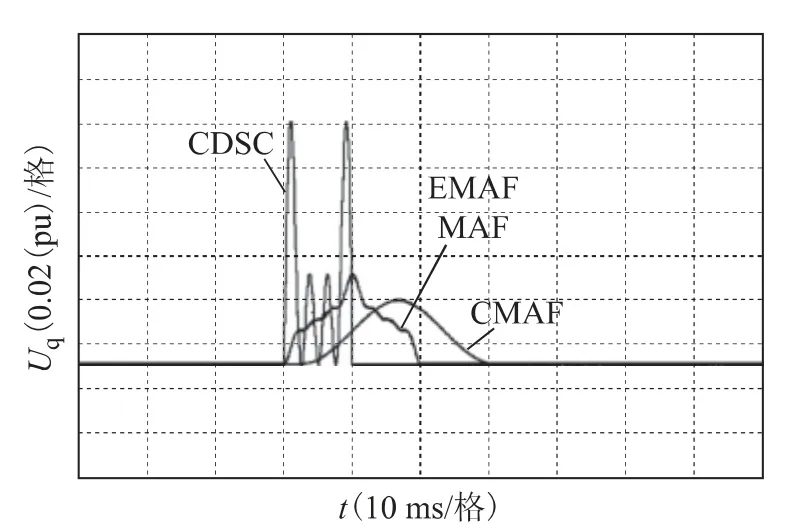
图9 滤除2、4、6、8 次谐波Fig.9 Eliminate the 2nd，4th，6thand 8thharmonics

实验结果表明:无论谐波有多少种类，EMAF、CDSC、MAF 算法滤除所有的偶次谐波分别仅需要1 个、0.5 个、1 个工频周期，而CMAF 算法的响应时间与谐波种类密切相关，谐波种类越多，则响应时间也越长;此外，CDSC 算法输出相位的振荡幅度明显大于其他算法，即响应时间越短，通常相位振荡也越严重。

综合来看，CDSC 算法的响应速度明显大于其他算法，CMAF 算法的响应时间最长;从动态响应速度、暂态过程中的相位振荡幅度以及数字化实现的复杂程度上来看，EMAF 算法的综合优势最明显，宜优先选用。

4.3 实验场景3:滤除奇数次谐波

图10分别为EMAF、CDSC、CMAF、MAF 算法同时滤除3、5、7 次谐波时q 轴电压的计算结果，其响应时间分别为10 ms、7.5 ms、18.3 ms、20 ms;图11为同时滤除3、5、7、9 次谐波时的结果，其响应时间分别为10 ms、8.8 ms、20.5 ms、20 ms，基本与理论结果一致。

图10 滤除3、5、7 次谐波Fig.10 Eliminate the 3rd，5thand 7thharmonics

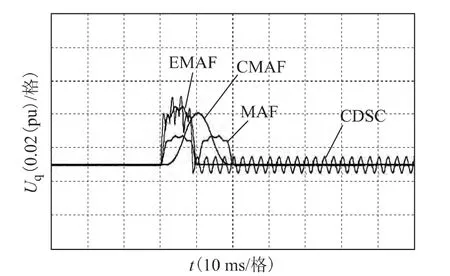
图11 滤除3、5、7、9 次谐波Fig.11 Eliminate the 3rd，5th，7thand 9thharmonics

实验结果表明:无论谐波有多少种类，EMAF、MAF 算法分别仅需0.5 个、1 个工频周期即可同时滤除所有的奇次谐波，而CDSC、CMAF 算法的响应时间则随谐波种类的增多而增长;此外，CDSC 算法的极限时间为0.5 个工频周期，而CMAF 算法的极限时间理论上趋于无穷大。

此外，图11中，CDSC 算法输出的q 轴电压含有8 次谐波(对应静止坐标系下的9 次谐波)，即稳态值不为0。采用CDSC 算法滤除8 次谐波，理论上需要延时12.5 个采样周期才能完全消除8 次谐波，对于数字控制系统而言，仅能延时整数个采样周期，即延时13或12 个周期，由此即导致了8 次谐波无法完全消除。

综合来看，在动态响应速度方面，CDSC 算法略优于EMAF 算法，且EMAF、CDSC 算法均明显优于CMAF、MAF 算法;从输出相位的暂态振荡幅度上看，CDSC 算法明显大于EMAF、CMAF、MAF 算法;考虑到EMAF 算法与CDSC 算法在响应时间上相近，且EMAF 算法的数字化实现最容易，输出相位波形的振荡幅度非常小，因此EMAF 算法的综合比较优势明显。

4.4 实验场景4:同时滤除一组奇次、偶次谐波

图12分别为EMAF、CDSC、CMAF、MAF 算法同时滤除8 次以内所有谐波时q 轴电压的实验波形，其响应时间分别为20 ms、17.5 ms、50 ms、20 ms，基本与理论时间一致。

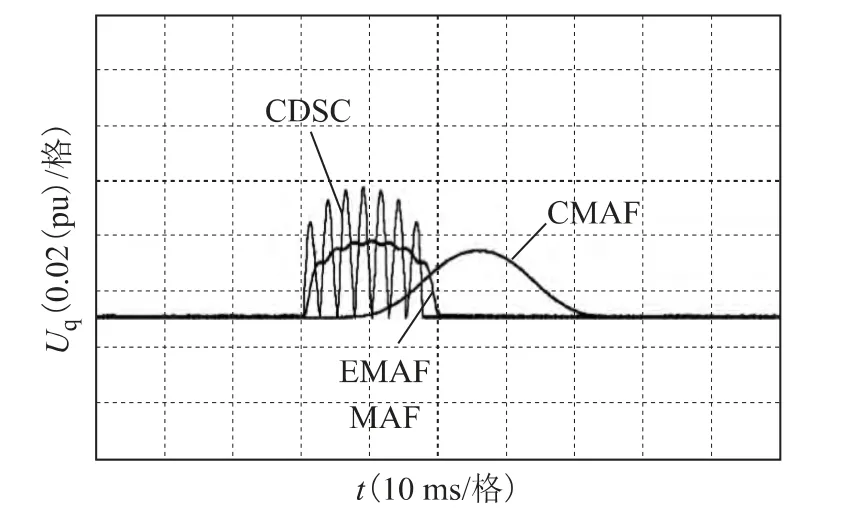
图12 滤除8 次以内的所有谐波Fig.12 Eliminate all the harmonics within 8th

实验结果表明:同时滤除任意次数的奇数、偶数次谐波时，EMAF 算法仅需要1 个滑动长度为电网工频周期的MAF 即可实现，而CDSC 算法则需要若干个不同滑动长度的DSC 级联，且响应时间随谐波种类的增多而增长，其极限时间也为1 个电网工频周期;虽然CDSC 算法的响应速度略优于EMAF 算法，但其输出相位的振荡幅度却远大于EMAF 算法。CMAF 算法依然是响应时间最长的。

综合来看，CDSC 算法的响应速度略有优势;EMAF 算法的输出相位波形受谐波影响的程度最小，暂态稳定性更佳;考虑到EMAF 算法在数字化实现上的显著优势，因此EMAF 算法的应用价值更大。

4.5 实验场景5:三相电网电压突然不对称

图13为三相电网电压突然不对称时，在EMAF 算法的作用下开环锁相方法输出的实时相位波形。实验结果表明:EMAF 算法以及基于EMAF 算法的快速开环锁相方法可在三相电网电压不对称的环境下快速获得准确的实时电网电压相位，能够有效消除同步旋转坐标系下负序分量导致的稳态锁相误差。

图13 电网电压突然不对称时的锁相结果Fig.13 Phase synchronization of unsymmetrical grid

图14为不对称电网下不同谐波消除算法输出的q 轴电压实时波形。显然，CDSC 算法的响应时间最短(5 ms)，暂态振荡幅度最大;MAF 算法的响应时间最长(20 ms)，但暂态振荡幅度最小;而EMAF、CMAF算法的综合性能最佳。

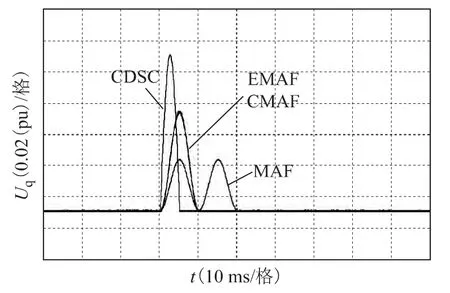
图14 不同算法下的q 轴电压波形Fig.14 Waveforms of Uqwith different algorithms

4.6 实验场景6:频率漂移且含有5 次谐波

图15、图16分别为电网频率由50 Hz 突变为40 Hz时基于EMAF 算法的快速开环锁相方法输出的相位波形以及不同算法下的q 轴电压波形。电网频率突变时，电网电压中同时注入了0.2(pu)的5 次谐波。实验表明:基于EMAF 算法的开环锁相方法获得了稳定且无稳态误差的相位信息，其动态响应时间约21 ms，其中频率检测约耗时15 ms。

图16 电网频率漂移时不同算法下的q 轴电压波形Fig.16 Waveforms of Uqwith different algorithms under frequency changing condition

分析实验结果可知:在突变频率被检测到之前，同步旋转坐标系下的电压基波分量为10 Hz 的低频交流量，导致输出相位波形出现了明显的振荡现象。在检测到突变频率后，控制系统调整了同步旋转坐标变换的频率以及EMAF 算法的滑动步长，因此同步旋转坐标系下的d、q分量重新恢复至直流形式，相位波形中的振荡现象也因此消失了。由此可知，在电网发生频率漂移时，通过检测并反馈实时的频率信息，并据此调整EMAF 算法的滑动长度即可使EMAF 算法实现频率自适应，并始终保持对谐波影响的有效滤除。

此外，EMAF、CDSC、CMAF 算法的动态响应时间相差不大，且均主要取决于频率检测过程的响应时间。图16表明CDSC 算法的暂态振荡现象依然最明显，MAF 算法的响应时间依然是最长的(约40 ms)，而EMAF 算法的响应时间约为20 ms，且q 轴电压波形较平滑。因此，EMAF 算法的综合性能最优，且数字化实现上也是最容易的。

5 结论

针对MAF 滑动长度的优化设计问题，通过量化分析得到了同时滤除若干指定次谐波时MAF 滑动长度应满足的充要条件，并据此提出了EMAF 算法以及基于EMAF 算法的畸变电网快速开环锁相方法。与经典的CDSC 方法相比，EMAF 算法的暂态振荡幅度远小于CDSC 方法，其谐波完全滤除能力明显强于CDSC 方法，且具备高频随机噪声抑制的能力，而CDSC 则无此功能。在响应速度方面，二者几乎相当，仅在滤除奇次谐波时响应速度慢于CDSC，考虑到并网变流器控制常在旋转坐标系下进行时(奇次谐波变成了偶次谐波)，EMAF 的响应速度则与CDSC 相等。此外，EMAF 算法的数据存储量以及数学运算次数等均远小于CDSC 算法，因而EMAF 算法在数字化实现上的优势十分明显。各种工况下的实验结果证明了分析结论的正确性以及改进方法的先进性。

需要说明的是:在处理多谐波问题时，EMAF 算法的响应速度较传统的MAF 算法有了显著提升，但在部分应用场合下依然略慢于经典的CDSC 算法，因此MAF 算法的性能依然需要进一步提升，尤其是动态响应速度。同时，如何将EMAF 算法与CDSC 算法的互补优势进行充分有效地结合，使多谐波消除算法的综合性能达到最优，这也是应深入研究的课题。此外，EMAF 算法也适用于其他涉及谐波信号处理的领域，例如:谐波检测与治理、故障在线诊断、继电保护整定、闭环锁相以及非理想电网条件下的并网变流器控制等。那么EMAF 算法在上述场合下的应用、与原系统进行整合、集成后的系统分析与设计以及系统整体性能的评估等问题均需要针对特定的应用场合分别进行研究，以充分发挥EMAF 算法的应用价值。

［1］ Divan D，Johal H．Distributed FACTS¯a new concept for realizing grid power flow control［J］．IEEE Transactions on Power Electronics，2007，22(6):2253-2260．

［2］ Johal H，Divan D．Design considerations for seriesconnected distributed FACTS converters［J］．IEEE Transactions on Industrial Applications，2007，43(4):1609-1618．

［3］ 张兴，张崇巍．PWM 整流器及其控制［M］．北京:机械工业出版社，2012．

［4］ 李珊瑚，杜雄，王莉萍，等．解耦多同步参考坐标系电网电压同步信号检测方法［J］．电工技术学报，2011，26(12):183-189．

Li Shanhu，Du Xiong，Wang Liping，et al．A grid voltage synchronization method based on decoupled multiple synchronous reference frame［J］．Transactions of China Electrotechnical Society，2011，26(12):183-189．

［5］ 袁志昌，宋强，刘文华．改善动态相位跟踪和不平衡电压检测性能的改进软锁相环算法［J］．电网技术，2010，34(1):31-35．

Yuan Zhichang，Song Qiang，Liu Wenhua．A modified soft phase lock loop algorithm improving the performance in dynamic phase tracking and detection of unbalanced voltage［J］．Power System Technology，2010，34(1):31-35．

［6］ 洪小圆，吕征宇．基于同步参考坐标系的三相数字锁相环［J］．电工技术学报，2012，27(11):203-210．

Hong Xiaoyuan，Lv Zhengyu．Three-phase digital phaselocked loop based on synchronous reference frame［J］．Transactions of China Electrotechnical Society，2012，27(11):203-210．

［7］ Freijedo F D，Doval-Gandoy J，Lopez O，et al．A generic open-loop algorithm for three-phase grid voltage/current synchronization with particular reference to phase，frequency，and amplitude estimation［J］．IEEE Transactions on Power Electronics，2009，24(1):94-107．

［8］ Wang L，Jiang J R，Hong L，et al．A novel phaselocked loop based on frequency detector and initial phase angle detector［J］．IEEE Transactions on Power Electronics，2013，28(10):4538-4549．

［9］ Golestan S，Ramezani M，Guerrero J M，et al．Moving average filter based phase-locked loops:performance analysis and design guidelines［J］．IEEE Transactions on Power Electronics，2014，29(6):2750-2763．

［10］ Robles E，Pou J，Ceballos S，et al．Frequency adaptive stationary reference frame grid voltage sequence detector for distributed generation systems［J］．IEEE Transactions on Industrial Electronics，2011，58(9):4275-4286．

［11］ 陆超，吴超，王天，等．多元自回归滑动平均模型辨识与电力系统自适应阻尼控制［J］．中国电机工程学报，2010，30(19):31-36．

Lu Chao，Wu Chao，Wang Tian，et al．Auto regressive moving averaging vector model identification and power system adaptive damping control［J］．Proceedings of the CSEE，2010，30(19):31-36．

［12］ Svensson J，Bongiorno M，Sannino A．Practical implementation of delayed signal cancellation method for phase sequence separation［J］．IEEE Transactions on Power Delivery，2007，22(1):18-26．

［13］ Bongiorno M，Svensson J，Sannino A．Effect of sampling frequency and harmonics on delay based phase sequence estimation method［J］．IEEE Transactions on Power Delivery，2008，23(3):1664-1672．

［14］ Neves F A S，Cavalcanti M C，de Souza H E P，et al．A generalized delayed signal cancellation method for detecting fundamental frequency positive sequence three phase signals［J］．IEEE Transactions on Power Delivery，2010，25(3):1816-1825．

［15］ 吴恒，杨东升，阮新波．基于串联信号延迟对消法的三相非理想电网锁相控制策略［J］．电工技术学报，2014，29(8):255-264．

Wu Heng，Yang Dongsheng，Ruan Xinbo．Phase-locked loop based on cascaded delayed signal cancellation for distorted grid［J］．Transactions of China Electrotechnical Society，2014，29(8):255-264．

［16］ Wang Yifei，Li Yunwei．Grid synchronization PLL based on cascaded delayed signal cancellation［J］．IEEE Transactions on Power Electronics，2011，26(7):1987-1997．

［17］ 陈明亮，肖飞，刘勇，等．一种正负序分离锁相环及其在并网型风力发电系统中的应用［J］．电工技术学报，2013，28(8):181-186．

Chen Mingliang，Xiao Fei，Liu Yong，et al．A positive and negative-sequence detection PLL and its applicationin wind power generation system［J］．Transactions of China Electrotechnical Society，2013，28(8):181-186．

［18］ Wang Yifei，Li Yunwei．Three-phase cascaded delayed signal cancellation PLL for fast selective harmonic detection［J］．IEEE Transactions on Industrial Electronics，2013，60(4):1452-1463．

［19］ Golestan S，Ramezani M，Guerrero J M，et al．dqframe cascaded delayed signal cancellation-based PLL:analysis，design，and comparison with moving average filter-based PLL［J］．IEEE Transactions on Power Electronics，2015，30(3):1618-1632．

［20］ Lee Kyoung-Jun，Lee Jong-Pil，Shin Dongsul，et al．A novel grid synchronization PLL method based on adaptive low-pass notch filter for grid-connected PCS［J］．IEEE Transactions on Industrial Electronics，，2014，61(1):292-300．