模块化多电平变换器的环流谐波抑制策略

张 明 吴浩伟 蔡 凯 徐正喜

(武汉第二船舶设计研究所 武汉 430205)

0 引言

多电平变换器由于其较低的电压应力，在高压大功率领域得到了广泛关注，在这些多电平拓扑结构中，二极管钳位型(Neutral-Point-Clamp，NPC)、电容钳位型(Float-Capacitor-Clamp，FCC)和级联型(Cascaded-Modular-Clamp，CMC)拓扑结构最为成熟，并在电机驱动、无功补偿、电气牵引、有源电力滤波和分布式发电等场合得到了广泛应用［1，2］。但NPC 型和FCC 型结构由于损耗分布不均、电气连接困难以及电压均衡等问题，很难扩展到三电平和四电平以上;而CMC 型结构则需要大量变压器绕组来为各功率模块提供隔离直流电源，其变压器设计非常复杂，且体积庞大、功率密度较低。

模块化多电平变换器(Modular Multilevel Converter，MMC)是新一代多电平拓扑结构，其在拓扑结构上具有模块化特征，易于实现“积木式”的电压等级扩展和电平数量扩展，并且由于多电平的输出特征，其具有极低的输出谐波，这允许功率器件在极低的开关频率下即可满足输出电能质量要求，因此MMC 具有相对较好的热设计和较高的变换效率。此外，MMC 无需借助变压器来实现电压匹配，能够直接连接至高压网络，能够更好地适应高压应用场合。上述这些因素使得MMC 在未来高压大功率领域具有很好的研究价值和应用潜力。

近年来，MMC 得到了快速发展，国内外众多学者对其进行了深入的研究和分析，包括建模方法［3］、快速仿真技术［4］、调制策略［5-7］、电压均衡方法［8，9］、环流谐波控制技术［9-14］以及MMC 在不同场合下的应用。MMC 被广泛应用于柔性直流输电(VSC-HVDC)工程，并在诸多实验中被应用于无功补偿、牵引电源以及电机驱动等，MMC 正在大量领域中发挥其优势［15-19］。

不同于传统的电压源变换器，负载中的基波电流流经桥臂后，会在子模块的电压中引入谐波扰动项。该谐波扰动项导致桥臂输出之间与直流侧之间的电压不再平衡，进而在环流中产生大量低次谐波，引起系统特性恶化、容量降低等。由于其低次特性，无源滤波方法难以得到较好的抑制效果，因此有必要研究该环流谐波的有源抑制方法。文献［9］将环流谐波扰动项定义为二次谐波分量，并在二次逆序旋转坐标系中对其进行了很好的抑制。

本文在考虑子模块电压扰动的基础上，进一步提出更加精确的环流控制模型，并提出基于谐振控制的抑制策略。该方法能对指定阶次的环流谐波扰动项进行有效抑制，通过多阶次谐振控制器的并联，即可实现对不同阶次扰动的同时抑制。为了实现对几乎所有阶次的抑制效果，获得更好的稳态结果，进一步将重复控制器引入环流控制中，来实现该目的。重复控制器形式简单，且适用于单相或多相MMC 变流系统，具有较好的通用性和相对更好的抑制效果。最后，建立了三相MMC 的实验平台，对所提出的多谐振抑制方法和重复控制抑制方法进行了相关验证和性能对比。

1 环流控制等效模型

图1a 为模块化多电平变换器(MMC)的基本拓扑结构，由3 个相单元(Phase-leg)构成，每个相单元由上下两个完全相同的桥臂(Arm)串联组成。每个桥臂则由一个桥臂电感(Arm Inductor)和N 个完全相同的子模块(SM)串联。图1b 为子模块的基本结构，它由一个半桥(S1和S2)和一个直流电容器(Csm)构成，可等价为一个电压斩波单元，其输出状态由互补工作的开关对S1-S2的状态所决定，当S1开通、S2关闭时，子模块输出电压(vsmo)为直流电容电压，此时子模块电容插入到桥臂中，其电压受到桥臂电流的充放电影响;反之，当S1关闭、S2开通时，子模块输出电压为零，子模块电容被旁路，其电压保持不变。K2为高速旁路开关，在子模块故障情况下，K2闭合以旁路该子模块。K1为晶闸管，用于在较高故障电流情况下保护功率器件，由于IGBT 载流能力相对较差，难以维持非常高的故障电流，此时需要开通K1来承担大部分故障电流，用以保护IGBT 免于损坏。

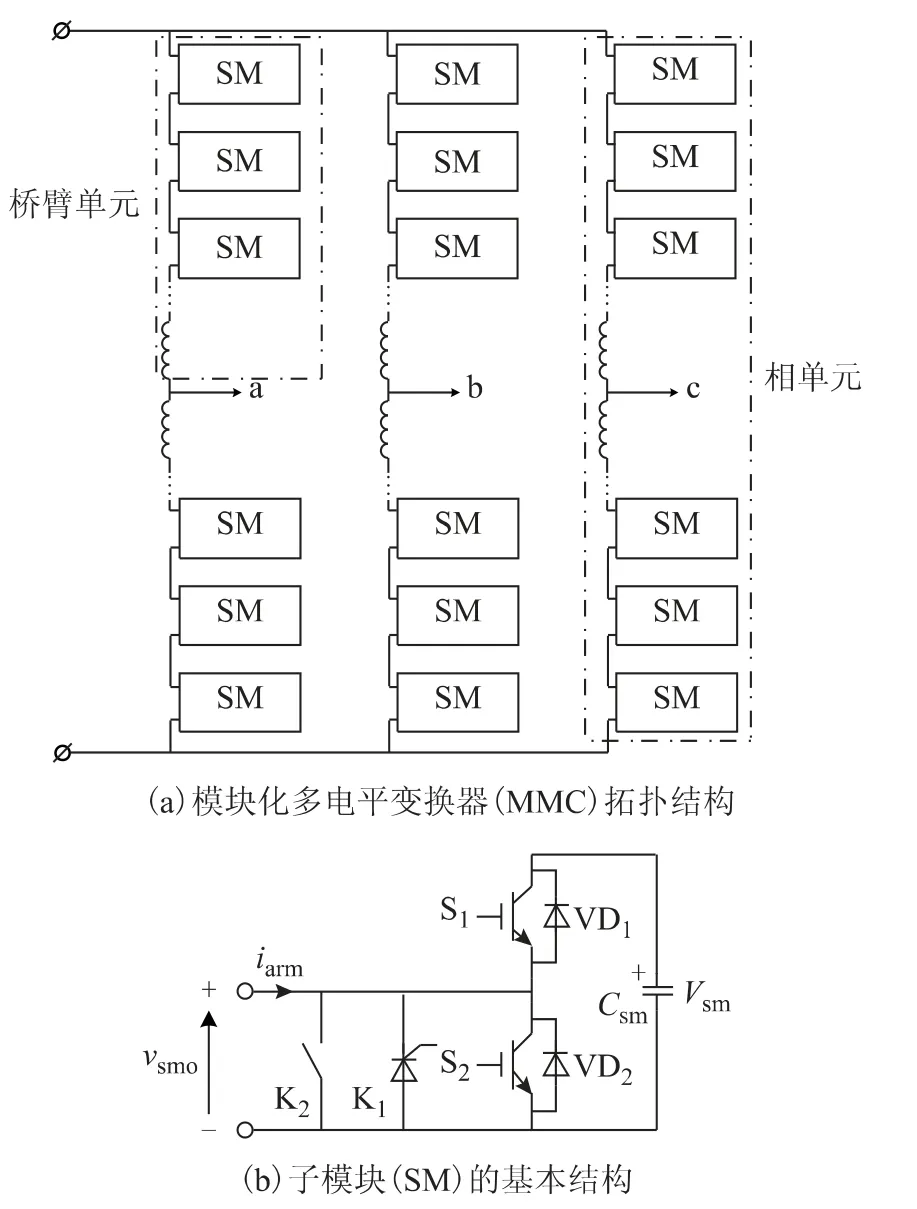
图1 模块化多电平变换器的基本结构Fig.1 The modular multilevel converter(MMC)topology

为了简化分析，将所有子模块等效为统一模型，由于三相桥臂具有同一性，下文将以单相桥臂进行统一分析。如图2所示，Lr为桥臂电感，Rr为桥臂等效电阻，idiff为流经桥臂的环流，vi为第i 个子模块的输出电压，vCi为第i 个子模块的直流电容电压，vp、vn分别为上下桥臂的输出电压，ip、in分别为上下桥臂电流，i 为交流侧输出电流，e 为交流侧输出电压，C 为桥臂等效电容，Csm为子模块直流电容，Vdc为直流侧输入电压。环流的作用机理可以用式(1)进行描述。

为了简化分析，作如下假设:①所有子模块均为理想的，且其电压在平衡控制基础上已保持平衡，即同一桥臂内的所有子模块具有相同电压;②系统所有损耗用桥臂等效电阻Rr进行描述;③桥臂输出电压为其内部N 个子模块所均分;④仅考虑调制波中的基波分量，忽略由交流侧控制引入的谐波成分。

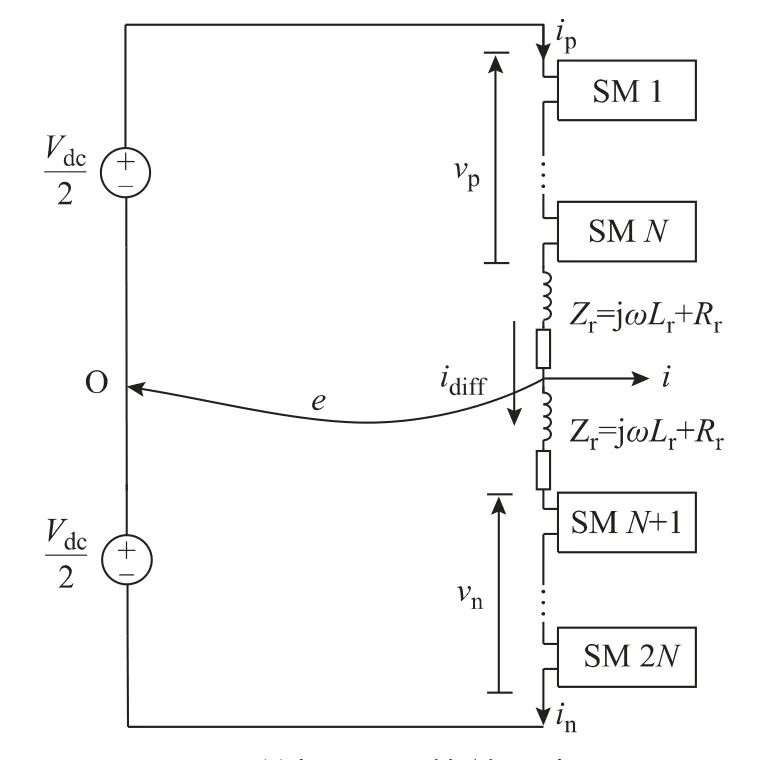
图2 单相MMC 等效示意图Fig.2 The equivalent circuit of single-phase MMC

桥臂等效电容C 为子模块电容Csm的1/N，定义输出电压、电流为

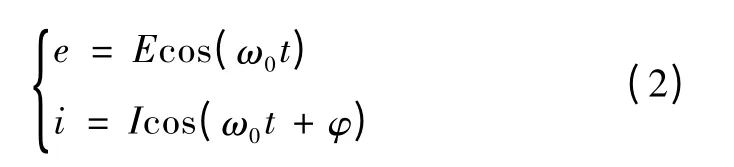
式中:ω0为输出角频率;E、I分别为交流侧输出电压、电流的幅值。输出调制函数可写为

式中M 为电压调制比。根据上下桥臂的输出参考电压vp和vn，其表达式如式(4)，可得到上下桥臂的调制函数为

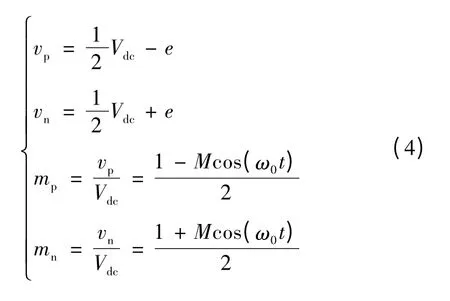
桥臂电流与环流及输出电流之间的关系可描述为

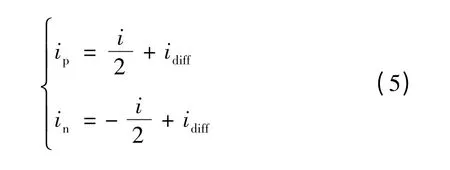
环流中包含有直流分量和各阶次的谐波分量，可写为

式中:Idc为环流中的直流分量，表征了直流侧与交流侧之间的有功交换;ik为环流中的k 次谐波分量，是由桥臂的调制过程所产生的;Ik和γk分别为第k 次谐波环流的幅值和初始相位。

定义上下桥臂子模块电压之和分别为vCp和vCn，其值与流经桥臂的电流和开通的子模块数量有关，任意时刻，桥臂的等效电容以及与vCp和vCn之间的数学关系可写为

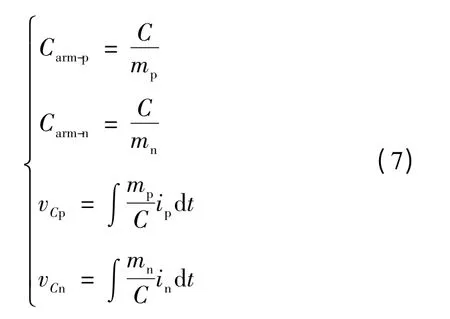
将式(2)～式(6)代入式(7)，可得到如下结果

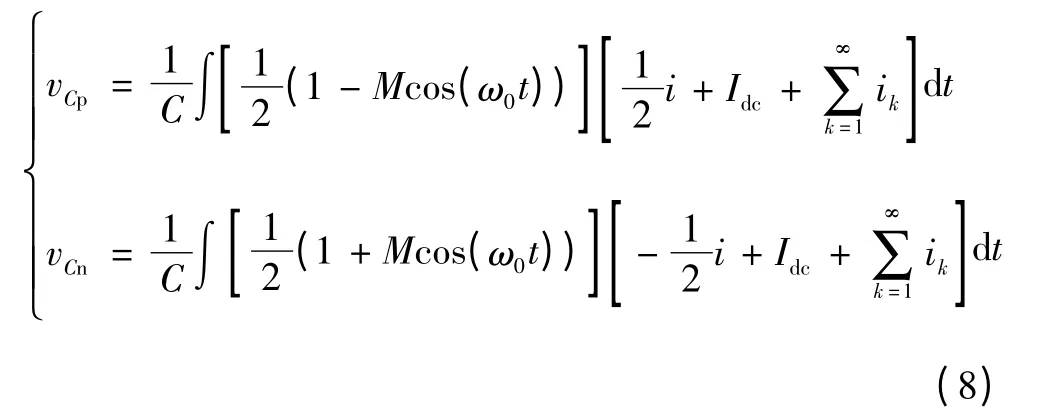
稳态下，式(8)中的积分项中应不包含直流成分，否则桥臂电压将趋于无穷大而失去稳定，因此根据直流项为零的结果，可进一步推导出环流中的直流成分Idc与系统交流侧有功功率之间的关系以及环流中的基波分量与输出电压相位正交的结论。稳态下，由于上下桥臂电压相等，环流中应不包含基波分量。从式(8)结果可进一步得到上下桥臂输出的实际电压为

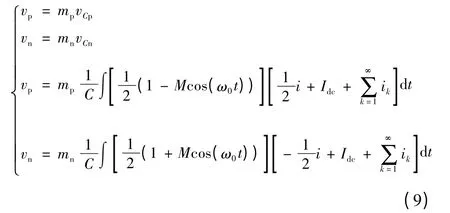
基于式(9)，可计算出上下桥臂输出电压之和为

将式(2)、式(3)、式(6)代入式(10)，可将桥臂输出电压整理为如下结果

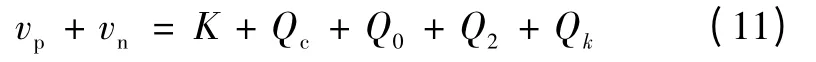
式(11)中各分量的结果为

式中:K 为积分初始值，其值理论上应为Vdc;Qc为常数，表明系统无功功率对桥臂输出电压的影响，该值为一个恒定值;Q0为一常数积分项，表征了系统有功与环流直流分量之间的关系，稳态下，该值应为零，否则系统失去稳定;Q2为桥臂输出电压中的二次谐波分量;Qk表征了环流中谐波成分的耦合作用，可看出，若环流中存在k 次谐波成分(即Ik＞0)，则会在桥臂输出电压中进一步衍生出(k－2)次和(k+2)次谐波成分。因此，负载电流引入的2 次谐波成分(即Q2项)，经过Qk项的耦合作用后，会进一步产生直流分量(即Qc项)和更高阶次的4 次谐波，类似地，该4 次谐波将进一步产生更高阶次的6 次谐波，等等，因此，稳态下，环流中存在着丰富的偶次谐波。

基于上述分析，稳态下，可认为桥臂的输出电压为

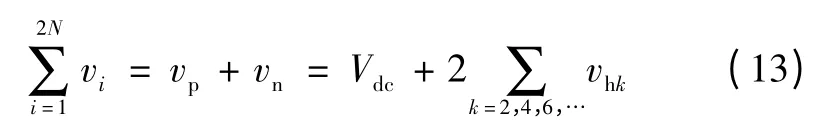
式中vhk为桥臂输出的偶次电压谐波项，为环流中谐波产生的根源。环流的控制是为了保证MMC 直流侧与交流侧之间稳定的有功交换，从而实现子模块电压稳定于其额定值。环流控制的结果是在上下桥臂输出电压中注入相同的电压分量vdiff，如式(14)所示。

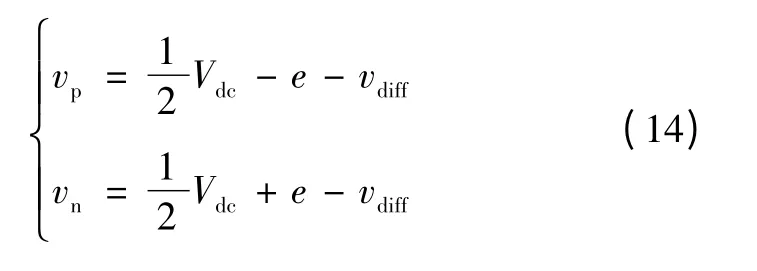
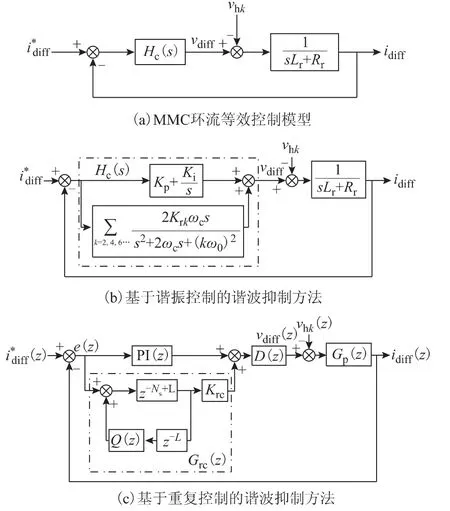
图3 MMC 的环流控制模型及其谐波抑制方法Fig.3 The circulation control model and its harmonics suppression methods of MMC

2 环流谐波抑制方法

从图3a 可看出，在控制环路内部存在偶次谐波扰动项vhn，而传统PI 控制器对其增益有限，因此vhn将在输出环流中产生大量谐波，谐波电流可写为

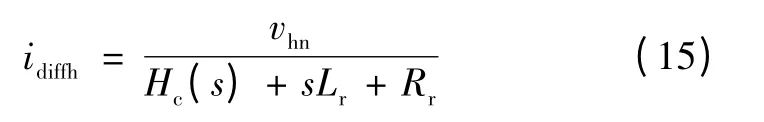
如果环流控制器Hc(s)对谐波频率处(例如2 次、4 次、6 次等)的增益较低，则通过式(15)可知，环流中对应频率的谐波电流较大。为了提供对指定阶次频率的高增益，可将谐振控制器引入到环流控制中，与传统PI 控制器形成互补，其结构如图3b 所示。其中，ωc为谐振控制器的带宽，Kr为其增益，k 为需要抑制的环流谐波阶次。当仅需要抑制环流中的主要谐波成分，即二次谐波时，可在环流控制器中加入二次谐振环节，如果需要更好的抑制效果，实现对多阶次的消除，可适当加入多个谐振环节。注意到，过多阶次谐振环节的加入会导致系统控制结构复杂，且对于系统控制稳定性不利，因此谐振控制器的数量和稳态性能需要折中考虑。

为了获得相对更优的稳态特性，实现对所有阶次的有效抑制，本文进一步将重复控制器引入到环流控制中，如图3c 所示。重复控制基于内模原理，可在指定频率处及其谐波频率处提供近似无穷大的增益，因此被广泛应用于跟踪周期性信号，以获得零稳态误差。重复控制通常由数字方法实现，因此为了更精确的理论分析与稳定性设计，下面将在离散域中直接进行相关分析，如图3c 所示。

重复控制器Grc(z)与PI 控制器PI(z)并联，D(z)为数字控制器的单位延时，Gp(z)为环流阻抗的传递函数，它们可描述为

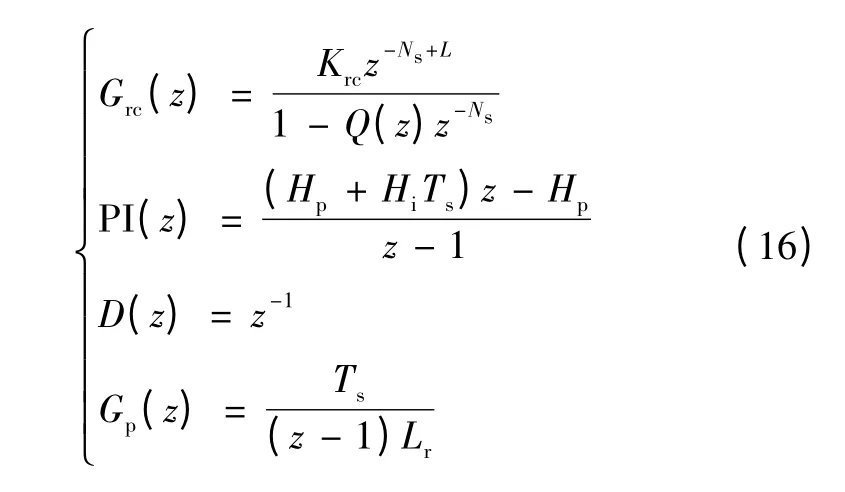
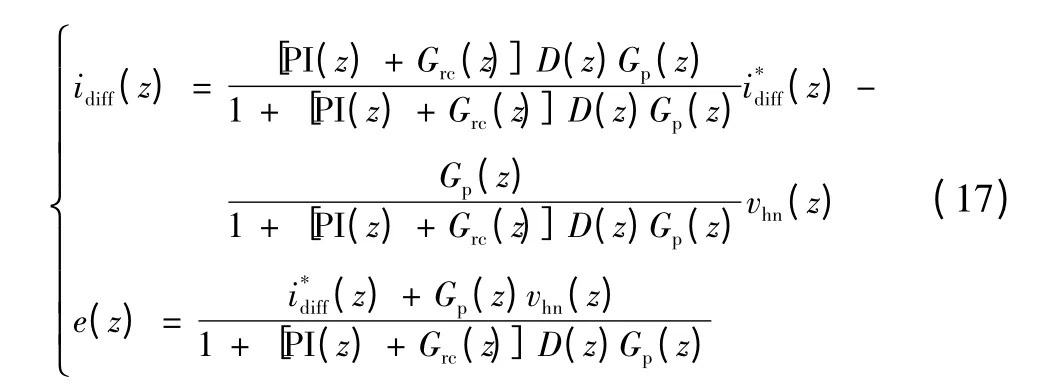
从式(17)中误差项可看出，重复控制器在所有阶次频率处都能提供较大的增益，能够有效抑制电压谐波扰动项vhn对输出环流的影响。

为了满足环流控制稳定性，误差函数e(z)的闭环特征根应在单位圆内，为了简化分析，定义

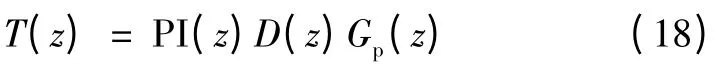
则误差函数e(z)的特征多项式E(z)可写为

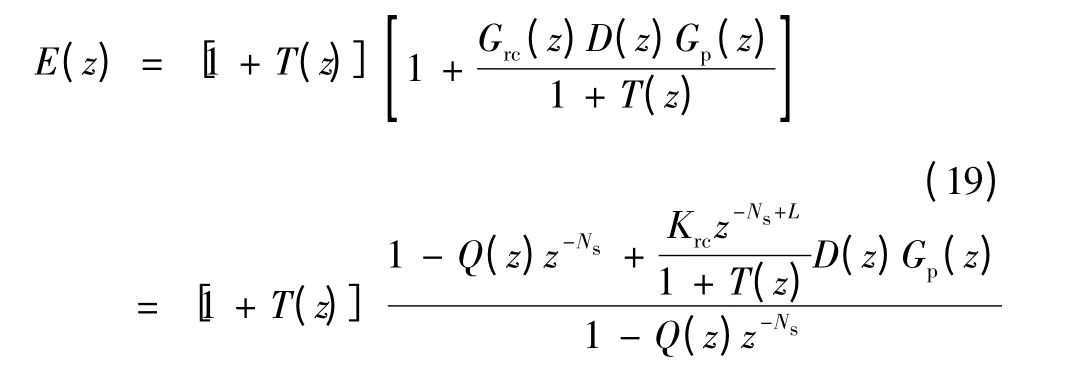
定义

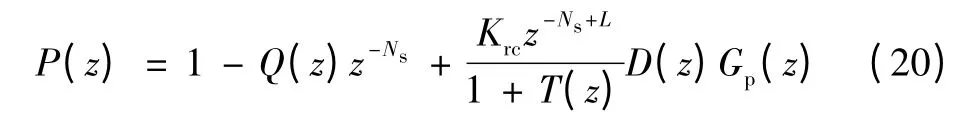
为了满足稳定性条件，即E(z)的零点在单位圆内部，需要满足如下条件:

1)多项式1+T(z)的零点要在单位圆内，这表明，在加入重复控制器之前，环流控制器应是稳定的。

2)多项式P(z)的零点要在单位圆内。

重复控制器的设计应满足第二个条件，进一步地，定义如下变量

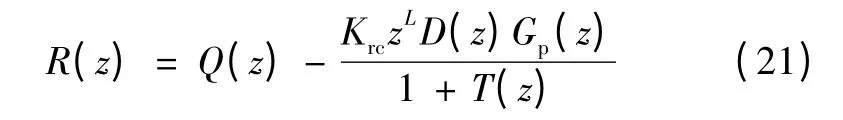
P(z)可改写为如下形式

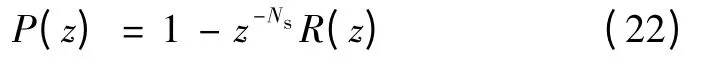
稳定性条件2)可进一步等价为如下条件:当R(z)在Nyquist 频率以下的频率范围内满足方程(23)时，系统是稳定的［20，21］。

离散域与频率之间的变换关系可写为

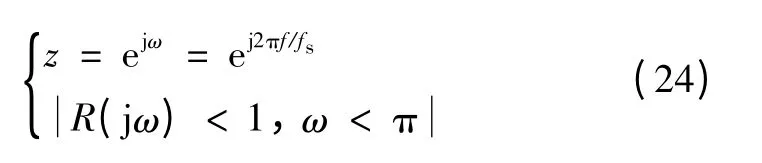
稳定滤波器Q(z)是一低通滤波器，为了补偿重复控制器自身位于单位圆周上的极点，通常该滤波器为一小于1 的常数(如0.95)，或具有零相位延迟的梳妆滤波器

式中F 为大于2 的整数。梳妆滤波器具有更优的稳态特性和高频衰减特性，本文将梳状滤波器应用于Q(z)，并取F=4，以获得较好的高频衰减特性。在选取Q(z)后，R(z)可写为

将上述多项式由离散域变换为频率，并写为幅度-相位形式，变换结果为

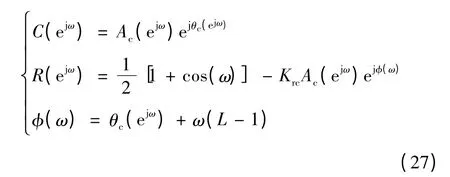
将式(27)代入式(23)可得出稳定性条件为

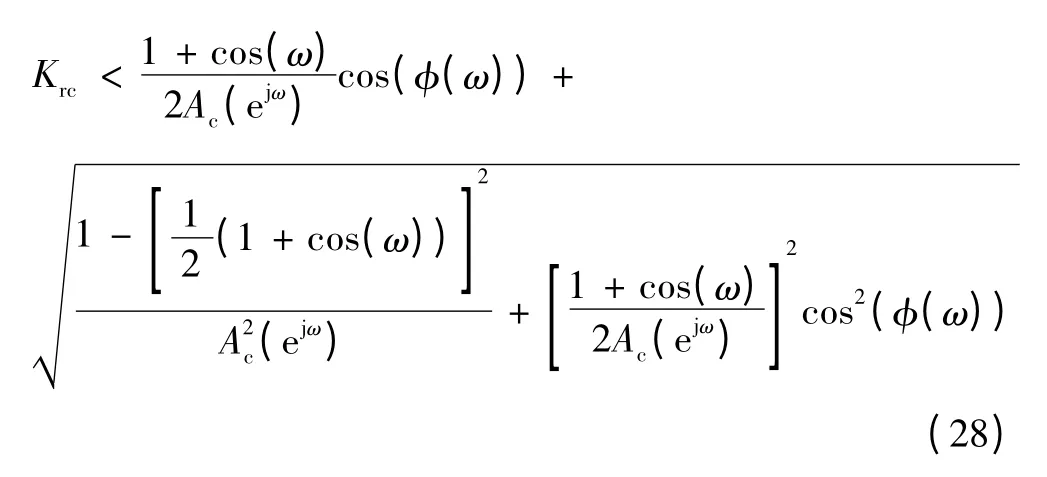
3 控制器参数设计

上面给出了谐振控制和重复控制的基本形式以及重复控制器的稳定性条件。本节将基于实际的样机参数给出控制器的参数设计过程。

表1 为样机的具体参数，控制器和调制器基于DSP(TMS320F28335)和FPGA(Cyclone ⅢEP3C25Q240)实现。在设计前，需要对PI 控制器进行设计，确保环路控制是稳定的，PI 控制器的设计带宽/相位裕度为500 Hz/45°，其参数见表2。

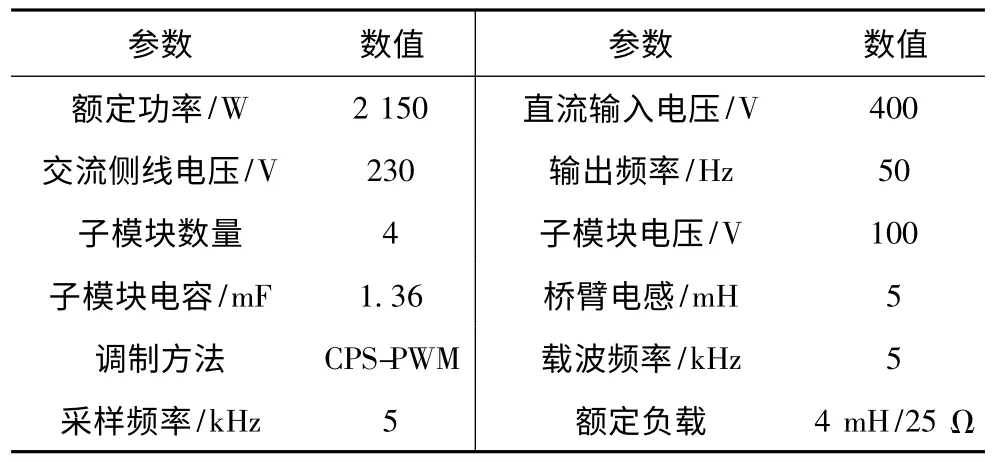
表1 样机参数Tab.1 Prototype parameters

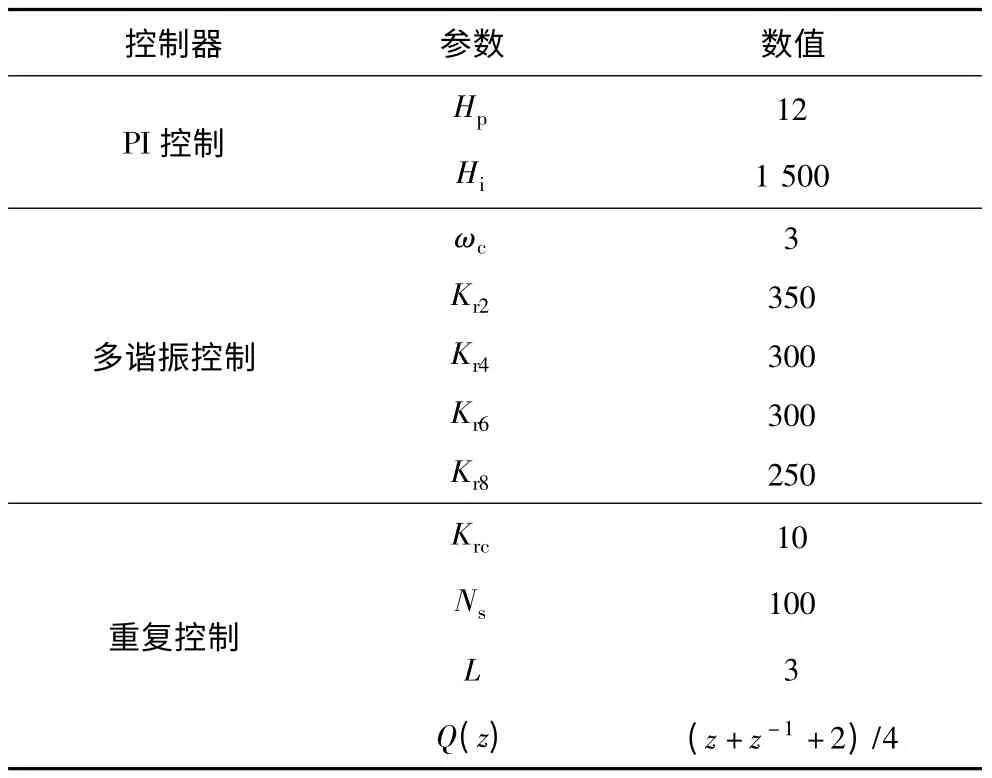
表2 环流控制器参数Tab.2 Circulating controller parameters

在不同的超前周期L 下，增益Krc的取值范围不同，为了获得更好的稳态抑制能力，Krc的取值应尽可能大。L 的取值很简单，该相位超前是为了弥补数字控制器延迟和电感相位滞后而引入的，以本文为例，可简单选择L=2。更精确地，可选择L=2 附近的值，观察增益Krc的选择范围，如图4所示。当L=3时，增益最大可达到15 左右，考虑到模型误差带来的影响，实际中选取Krc=10。基于上述设计结果，可以对加入重复控制器后的环流对电压谐波的导纳-频谱进行计算，如图5所示，对比曲线为仅加入PI 控制的导纳值。从图5可看出，加入重复控制后，输出环流对电压谐波扰动在指定阶次及其谐波阶次的衰减非常大，而传统PI 控制对此则基本无衰减。与此类似，多谐振控制只能在有限的几个频率点提供衰减，其抑制效果不如重复控制全面。表2 仅给出了环流控制器的相关参数，包括PI 控制器、各阶次的谐振控制器和重复控制器，其余控制器的参数不做具体讨论。

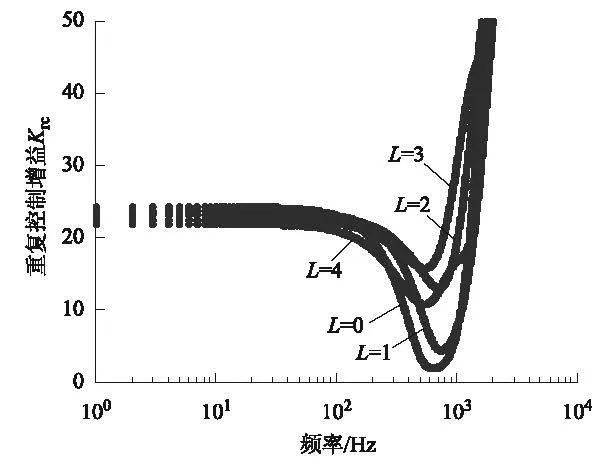
图4 不同超前周期数L 下的增益取值范围Fig.4 The gain limitation under different lead cycles

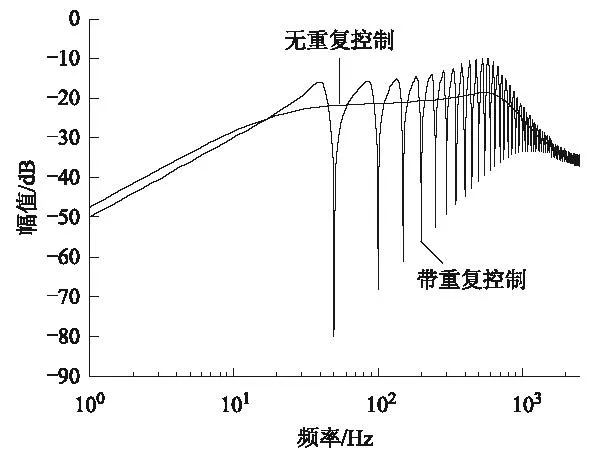
图5 重复控制与传统PI 控制的环流谐波抑制能力比较Fig.5 The circulating harmonics suppression comparison under repetitive controller and PI controller

4 实验结果

针对表1 所列参数，建立了三相MMC 实验平台，并在额定负载下对表2 所列的各种环流控制器进行了相关实验。环流控制器共采用了6 种方案:①比例-积分控制;②2 次谐振控制;③2 次+4 次谐振控制;④2 次+4 次+6 次谐振控制;⑤2 次+4 次+6 次+8 次谐振控制;⑥重复控制。

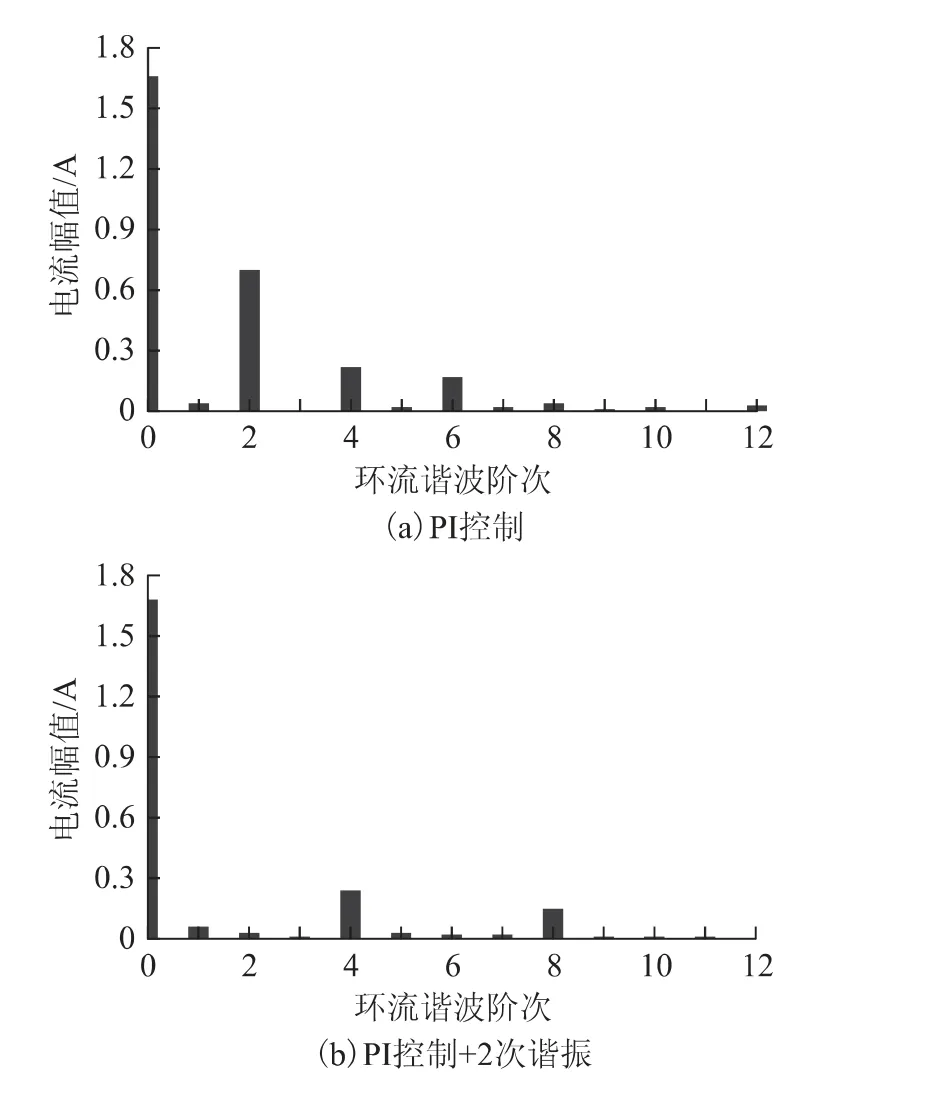
图6为上桥臂电流和环流波形的稳态波形对比结果，包括。图7为环流频谱的对比。从稳态结果可看出，当仅使用比例-积分控制时，环流中存在明显的2次、4 次、6 次谐波分量;当加入谐振控制后，部分低次谐波被消除，但仍存在明显的高次谐波分量，如8 次、10 次等。即使加入8 次谐振控制，10 次谐波依然存在，很难实现所有阶次的完全消除。图6f 和图7f分别为重复控制的环流和桥臂电流波形以及环流的频谱，可看到，环流中的谐波成分几乎完全消除，桥臂电流波形没有失真，为正弦。

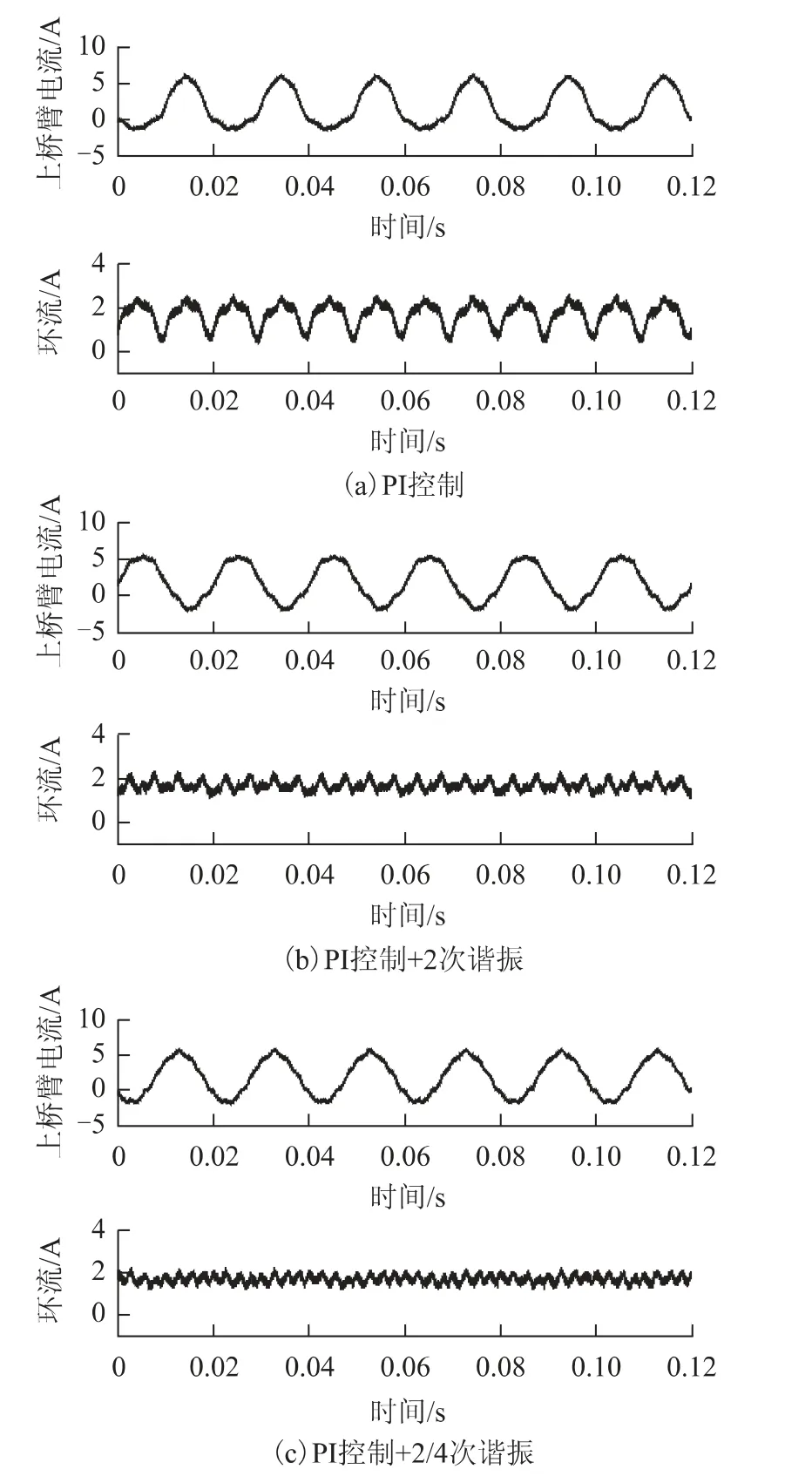
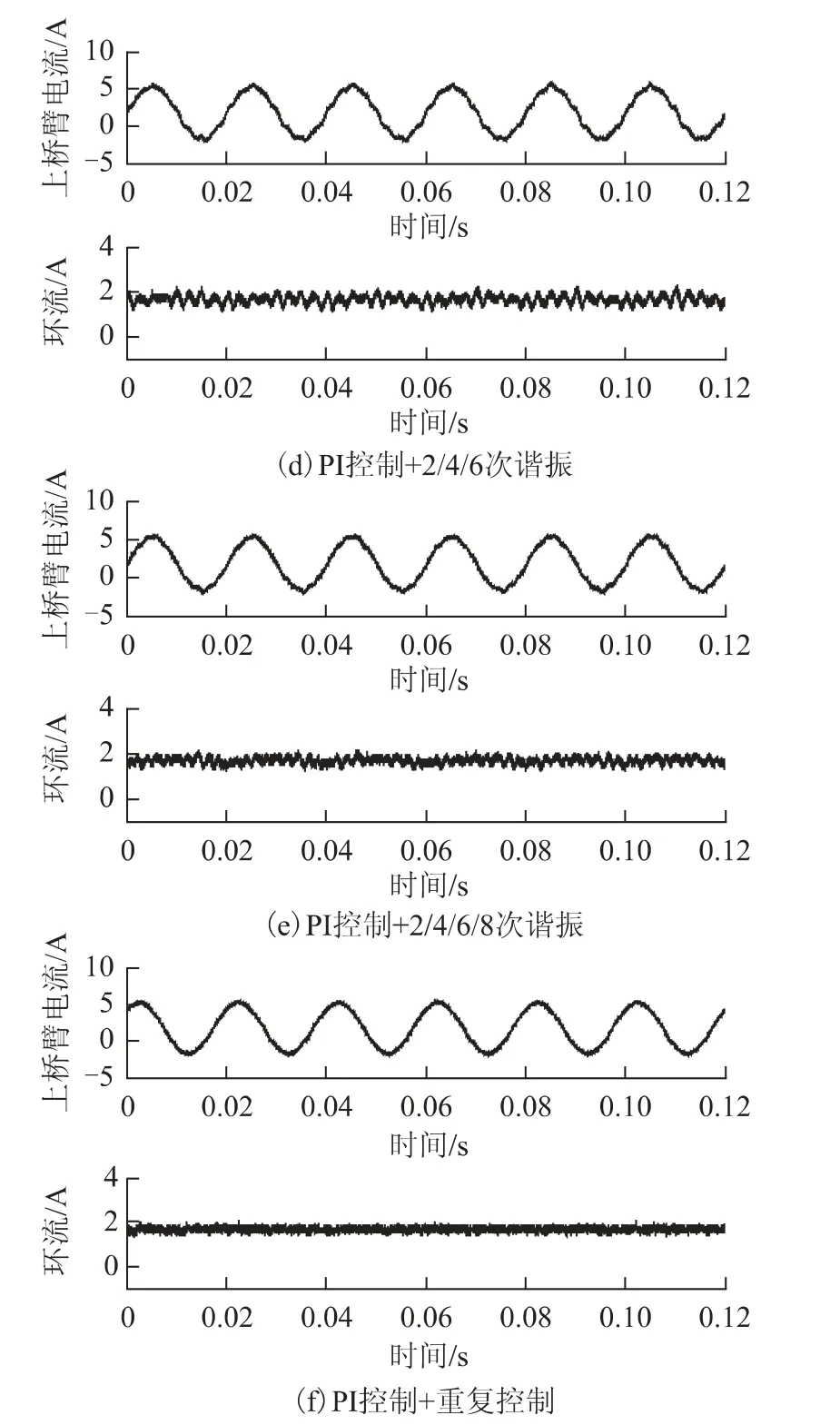
图6 不同环流控制器下的桥臂电流和环流波形对比Fig.6 The steady-state results of circulating current and arm current under different controllers

进一步地，对比例-积分控制和重复控制进行了动态特性对比。图8和图9分别为在负载突变和电压调制比突变情形下的动态过程，可明显看出，重复控制器的加入并未对动态过程产生太大影响。由于重复控制器需要滞后一个周波才能产生作用，在这段时间内，环流的响应与PI 控制器基本一致，经过一个周波后，重复控制器将使环流控制误差逐渐收敛至零，这可从实验波形中明显看出。

图8 重复控制与比例积分控制的动态特性对比Fig.8 The transient results comparison under load step between the repetitive controller and the PI controller

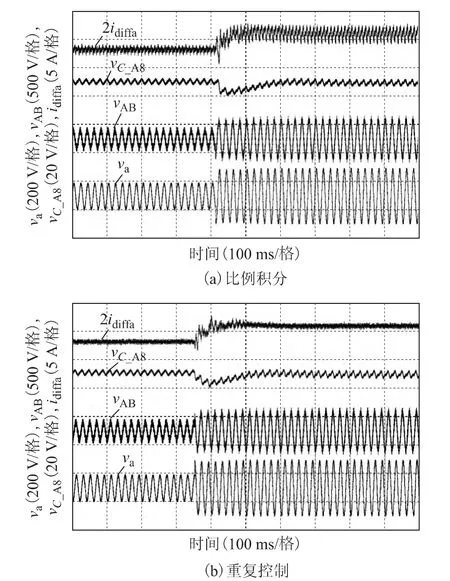
图9 重复控制与比例积分控制的动态特性对比:电压调制比从0.5 跳变到1Fig.9 The transient results comparison under voltage modulation index step from 0.5 to 1

实验结果显示，谐振控制器和重复控制器都能对MMC 的桥臂环流谐波进行有效抑制，且重复控制器具有相对更优的稳态效果，几乎能够实现环流谐波成分的完全消除，且其动态特性无太大改变，稳态、动态性能较为优秀。实验结果证明了本文所提环流谐波抑制方法的有效性。

5 结论

本文对模块化多电平变换器(MMC)的环流谐波抑制方法进行了讨论和研究，并给出了基于谐振方法和重复控制方法的抑制策略。首先，建立了MMC 的环流等效控制模型，并系统研究了环流谐波产生的根源及其不同阶次之间的耦合效应。其次，通过增大控制环的谐波阻抗来减小输出环流谐波，本文提出了基于谐振控制器的抑制方法，为了获得更优的稳态抑制效果，进一步将重复控制器引入，实现所有谐波阶次的同时抑制，并深入分析了环流控制的稳定性问题。最后，基于样机参数给出了环流控制器的参数设计过程，并采用多种方法实现了环流谐波的抑制，并完成了稳态特性和动态特性的对比，进一步验证了所提方法的可行性和有效性。

［1］ Rodriguez J，Bernet S，Wu B，et al．Multilevel voltage-source-converter topologies for industrial mediumvoltage drives［J］．IEEE Transactions on Industrial Electronics，2007，54(6):2930-2945．

［2］ Rodriguez J，Lai J S，Peng F Z．Multilevel inverters:a survey of topologies，controls，and applications［J］．IEEE Transactions on Industrial Electronics，2002，49(4):724-738．

［3］ Ilves K，Antonopoulos A，Norrga S，et al．Steady-state analysis of interaction between harmonic components of arm and line quantities of modular multilevel converters［J］．IEEE Transactions on Power Electronics，2012，27(1):57-68．

［4］ Xu Jianzhong，Zhao Chengyong，Liu Wenjing，et al．Accelerated model of modular multilevel converters in PSCAD/EMTDC［J］．IEEE Transactions on Power Delivery，2013，28(1):129-136．

［5］ Li Z，Wang P，Zhu H，et al．An improved pulse width modulation method for chopper-cell-based modular multilevel converters［J］．IEEE Transactions on Power Electronics，2012，27(8):3472-3481．

［6］ 王晓鹏，杨晓峰，范文宝，等．模块组合多电平变换器的脉冲调制方案对比［J］．电工技术学报，2011，26(5):28-33．

Wang Xiaopeng，Yang Xiaofeng，Fan Wenbao，et al．A comparative study of multi-pulse modulation schemes for modular multilevel converters［J］．Transactions of China Electrotechnical Society，2011，26(5):28-33．

［7］ Hagiwara M，Maeda R，Akagi H．Control and analysis of the modular multilevel cascade converter based on double-star chopper-cells(MMCC-DSCC)［J］．IEEE Transactions on Power Electronics，2011，26(6):1649-1658．

［8］ Li Xiaoqian，Song Qiang，Li Jianguo，et al．Capacitor voltage balancing control based on CPS-PWM of modular multilevel converter［C］．IEEE Energy Conversion Congress and Exposition(ECCE)，Phoenix，AZ，USA，2011:4029-4034．

［9］ Tu Q，Xu Z，Xu L．Reduced switching-frequency modulation and circulating current suppression for modular multilevel converters［J］．IEEE Transactions on Power Delivery，2011，26(3):2009-2017．

［10］ Li Zixin，Wang Ping，Chu Zunfang，et al．An inner current suppressing method for modular multilevel converters［J］．IEEE Transactions on Power Electronics，2013，28(11):4873-4879．

［11］ 陈耀军，陈柏超，袁佳歆，等．模块化多电平逆变器电容电压及环流控制［J］．电工技术学报，2014，29(10):166-174．

Chen Yaojun，Chen Bochao，Yuan Jiaxin，et al．The control of capacitor voltages and circulating currents of the modular multilevel inverter［J］．Transactions of China Electrotechnical Society，2014，29(10):166-174．

［12］ 高航，苏建徽，汪晶晶，等．模块化多电平型换流器电容电压二倍频波动抑制策略研究［J］．电力系统保护与控制，2014，42(6):116-122．

Gao Hang，Su Jianhui，Wang Jingjing，et al．Study on control strategy for suppressing double fundamental frequency fluctuation of capacitor voltage of modular multilevel converter［J］．Power System Protection and Control，2014，42(6):116-122．

［13］ 高建，苏建徽，高航，等．模块化多电平换流器电容电压与环流的控制策略［J］．电力系统保护与控制，2014，42(3):56-62．

Gao Jian，Su Jianhui，Gao Hang，et al．Capacitor voltage and circulation current control strategy in modular multilevel converter［J］．Power System Protection and Control，2014，42(3):56-62．

［14］ 卓谷颖，江道灼，连霄壤．模块化多电平换流器不平衡环流抑制研究［J］．电力系统保护与控制，2012，40(24):118-124．

Zhuo Guying，Jiang Daozhuo，Lian Xiaorang．Study of unbalanced circular current suppressing for modular multilevel converter［J］．Power System Protection and Control，2012，40(24):118-124．

［15］ Peralta J，Saad H，Dennetière S，et al．Detailed and averaged models for a 401-Level MMC-HVDC system［J］．IEEE Transactions on Power Delivery，2012，27(3):1501-1508．

［16］ 王奎，郑泽东，李永东．基于新型模块化多电平变换器的五电平PWM 整流器［J］．电工技术学报，2011，26(5):34-38．

Wang Kui，Zheng Zedong，Li Yongdong．A five-level PWM rectifier based on new modular multilevel converter［J］．Transactions of China Electrotechnical Society，2011，26(5):34-38．

［17］ Hagiwara M，Nishimura K，Akagi H．A mediumvoltage motor drive with a modular multilevel PWM inverter［J］．IEEE Transactions on Power Electronics，2010，25(7):1786-1799．

［18］ Mohammadi H P，Bina M T．A transformerless mediumvoltage STATCOM topology based on extended modular multilevel converters［J］．IEEE Transactions on Power Electronics，2011，26(5):1534-1545．

［19］ Hagiwara M，Maeda R，Akagi H．Negative-sequence reactive-power control by a PWM STATCOM based on a modular multilevel cascade converter(MMCC-SDBC)［J］．IEEE Transactions on Industrial Application，2012，48(2):720-729．

［20］ Mattavelli P，Tubiana L，Zigliotto M．Torque-ripple reduction in PM synchronous motor drives using repetitive current control［J］．Transactions on Power Electronics，2005，20(6):1423-1431．

［21］ Zhou K，Wang D．Digital repetitive controlled threephase PWM rectifier［J］．IEEE Transactions on Power Electronics，2003，18(1):309-316．