功率器件集总参数热路模型及其参数提取研究

万 萌 应展烽 张旭东 吴军基 杨忠浩

(南京理工大学能源与动力工程学院 南京 210094)

0 引言

随着电力电子技术迅速发展，MOSFET、IGBT 等功率器件的封装尺寸逐渐减小，但功率等级和热流密度却逐步提高，易发生因高温引起的各种失效故障［1，2］。因此，有必要实时获知功率器件工作温度，实现相应的主动热控制和过热保护［3-5］，提高器件运行可靠性。

在工程中，功率器件的芯片结点温度通常难以直接测量［6-11］，故人们更加关注器件壳体温度。只要保证壳体温度不超过预先设定的最大允许值，功率器件便可稳定运行。从实现角度看，温度探头接触式测量和红外非接触式测量是两类常用的直接测温手段。但对于分立型功率器件而言，上述测温方法在实际使用中存在一定弊端。例如，为保证精度，接触式测量要求温度探头安装在功率器件外壳上，但分立器件体积相对小巧，探头缺乏有效固定位置，极易发生脱落或错位现象，导致测温失败。尤其当功率设备被置于振动强烈的环境中工作时，温度探头测温的可靠性将进一步下降。非接触式测量要求红外传感器必须垂直对准被测物体，二者之间不能存在遮挡，这不利于功率设备内部元件的优化布局。此外，红外传感器还会受到环境温度和灰尘干扰的影响，精度易发生漂移，测量结果误差较大［12］。上述原因导致当前中低速电动车控制器和便携式逆变器等功率设备普遍未对功率器件的工作温度进行测量，因此难以实现器件的主动热控制，其过热保护也因缺乏数据难以准确判断。

事实上，若能通过实验离线建立准确的功率器件温度计算模型，便可通过软件方式对器件温升过程进行在线计算，避免在实际使用中直接测量功率器件温度，从而克服直接测温带来的弊端。文献［13，14］提出了将功率器件及其散热器视为整体的集总参数温升模型。这类集总参数模型具有计算方便及容易实现等优势，为器件的热动态分析提供了有效的工程方法。

但当前集总参数模型不是以功率器件热平衡原理为基础建立的，而是以实验中已经测量得到的温升曲线为对象建立的。模型能够描述器件温度随时间的变化关系，但这种描述必须建立在已有实验曲线的基础上，难以满足器件在不同运行条件下的温度计算要求，故具有一定局限性。造成这种现状的主要原因在于功率器件是由多种材料复合而成的［15］，材料之间存在接触热阻。接触热阻不仅与材料特性有关，也和材料之间接触面的粗糙度有关。因此，器件热平衡方程中的等效热容和热阻等参数难以确定。当加装散热器后，功率器件的热学参数将进一步改变，确定更加困难。

本文提出了基于热平衡原理的功率器件集总参数热路模型及其参数提取方法，克服了等效热路参数难以确定的问题。另外，因模型参数的提取可通过实验离线完成，故所提模型还可减少实际使用中，器件温度获取对传感器的依赖，尤其适合在传感器难以可靠固定和精度易发生漂移的场合中使用。

1 功率器件集总参数热路模型

功率器件在使用中通常加装散热器来增加散热面积，减少温升速率，降低工作温度，如图1所示。常用的散热器一般都能满足毕渥数Bi ＜0.1 条件，故其内部传导热阻可忽略，且能够和功率器件看作一个整体［16］。需要注意的是，功率器件焊接在电路板上，与电路板铜皮之间存在热传导和热辐射。然而，电路板并非热的良导体，其散热能力与线路布局及敷铜面积有关，因此在建立集总参数温升模型时，应当考虑器件与电路板之间的传热。

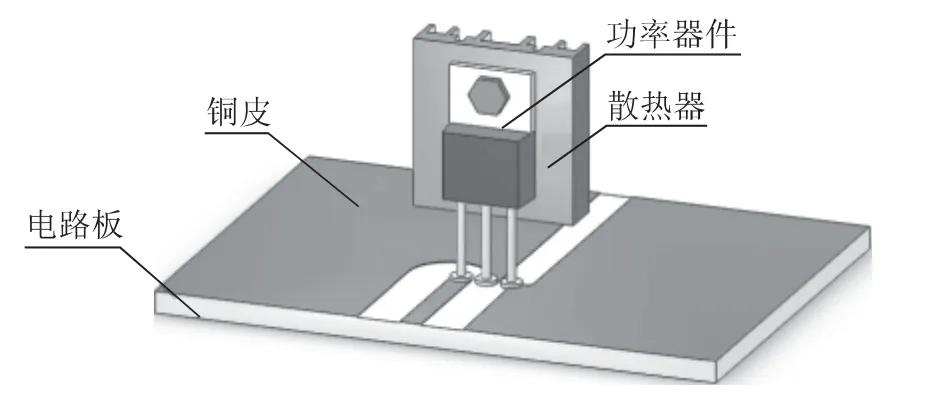
图1 功率器件及散热器示意图Fig.1 Schematic structure of power device mounted with heat sink

在此背景下，根据热平衡原理，可得功率器件非稳态热平衡方程为

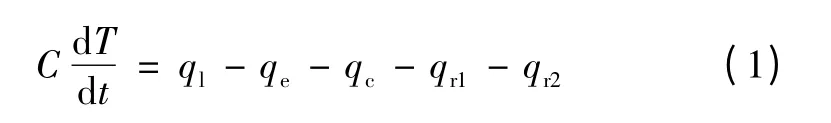
式中:t 为时间;T 为功率器件温度;C 为散热片与功率器件视为整体后的等效热容;ql为器件热损耗;qe为功率器件与周围环境之间的热对流;qc为功率器件与电路板之间的热传导;qr1和qr2分别为功率器件与周围空间及电路板之间的热辐射。

再根据热电类比理论［17，18］，物体之间的换热量qx可简化为欧姆定律形式

式中:Ta和Tb分别为两类物体的温度;Rx为物体之间的热阻，可综合包含对流、传导、辐射及日照等条件的影响［19］。

由此，建立功率器件温升的非稳态集总参数热路模型为

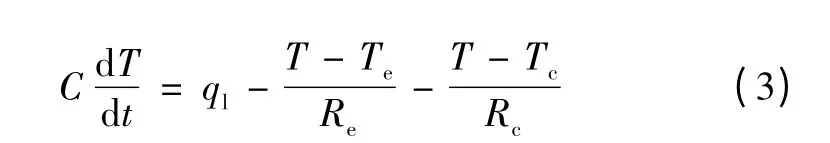
式中:Te为环境温度;Tc为功率器件管脚焊盘所处的电路板温度;Re为功率器件与环境之间换热的等效热阻，表征了周围空气热对流及热辐射对器件温度的影响;Rc为功率器件与电路板之间换热的等效热阻，表征了电路板的热传导及热辐射对器件温度的影响。

式(3)所示的集总参数热路模型可表示为图2所示的等效电路形式。由图中可见，若将ql、Te及Tc作为输入量，那么功率器件温升可视为一个多输入单输出电路系统的响应，其时间离散表达式为

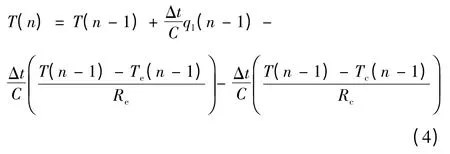
式中:n 为时间步数;Δt 为离散时间步长。

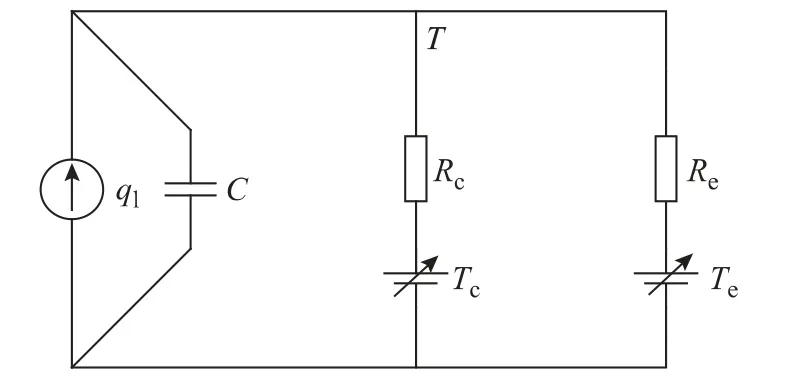
图2 热路模型的等效电路表示Fig.2 Equivalent circuit of thermal circuit model

式(4)表明，求解器件温升需获知输入量及模型参数。对于输入量而言，温度Te和Tc均可实际测量得到，而热损耗ql由器件的开通损耗、关断损耗和通态损耗组成，其理论计算方法可参考文献［20］。为突出研究重点，本文只考虑器件的通态损耗，故ql也可通过监测功率器件导通时的电流及漏源极电压得到。

模型参数的计算却相对困难，这不仅是因为器件材料的质量、比热容、对流换热系数和导热系数等数据难以获得，更是因为器件各层材料，包括外部加装散热器在内，相互之间均存在接触热阻，而这些接触热阻会因材料的热膨胀作用发生改变。尽管功率器件和散热器可被视为整体进行分析，但接触热阻的改变会影响器件的整体等效热学参数。接触热阻不仅和材料本身特性有关，也和材料之间接触面的粗糙度有关，目前为止还缺乏有效的理论计算方法，也难以直接测定，为此本文提出利用参数辨识方法来提取功率器件热路参数C、Re和Rc，克服参数计算困难的问题。

2 模型参数辨识方法

为辨识模型参数，以热路模型时域响应与实测结果之间的误差作为目标函数。根据线性系统理论，功率器件在n时刻的温升与此前时刻的温度及输入量相关联，故式(4)可改写为如下函数形式

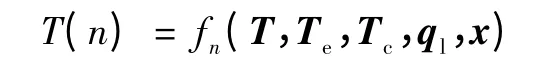
式中

那么，目标函数可表达为

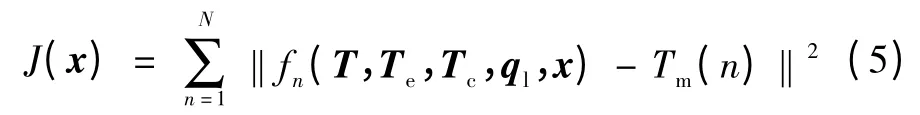
式中:x 为待辨识的模型参数矢量，x=［C，Re，Rc］;Tm(n)为n时刻的实测温度。若存在元素均非负的矢量x，使目标函数J(x)最小，则x 中的元素即为实际等效热路参数，材料间的接触热阻对参数的影响被隐含在辨识结果中。

考虑到遗传算法(GA)具有良好的全局搜索能力，不易陷入局部最优解，本文利用其寻找x 的最优值。GA 算法以达尔文进化理论为基础建立，将优化变量进行编码，成为带有遗传信息的个体。通过引入适者生存的计算法则，对种群内的个体进行选择、交叉和变异。经过若干代繁殖后，种群中最终剩下适应性最强的个体，该个体即为最优解［21，22］。算法的具体实现步骤如表1 所示。

表1 GA 算法实现步骤Tab.1 The steps of GA algorithm

GA 算法本质上属于概率型的搜索算法，其优化结果并非恒定值，故模型参数应通过多次优化平均后确定。另外，GA 算法结果精度与遗传算子的选择、交叉和变异算法类型有关，也和种群规模、交叉概率、变异概率等参数的选择有关。本文使用的GA 算法参数如表2 所示，实践表明，该算法精度满足功率器件温升模型参数的需要。

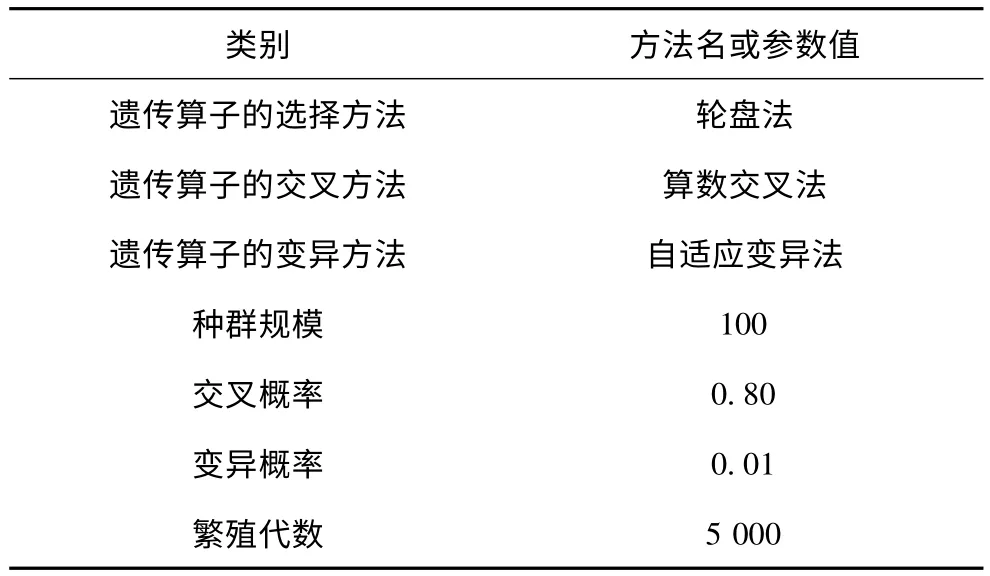
表2 GA 算法参数表Tab.2 The parameters of GA algorithm

3 实验平台设计

为实现参数提取，并验证模型精度，设计了如图3所示的功率器件温升实验平台。平台中，型号为AOT470 的功率MOSFET 被焊接在实验电路板上，其导通与关断状态受控于驱动控制系统。外部可调恒流源为功率器件提供工作电流，断路器为实验平台提供过电流保护。数据采集装置负责采集功率器件的温升T、电路板温升Tc、环境温度Te、器件电流I 及漏源极电压VDS等参数。实验数据通过串口通信上传至后台服务器进行存储及分析。

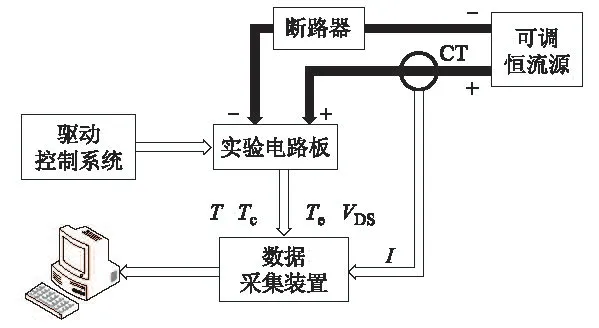
图3 实验平台结构示意图Fig.3 Block diagram of the experiment platform

实验平台中的温度测量元件采用MF52 微型温度探头，热时间常数＜5 s。实验前，探头通过标准水银温度计校准，测量误差小于1%，精度满足工程测量要求。实验中，用于测量功率器件温升的温度探头通过尼龙带固定在器件封装外壳上。因尼龙带宽度仅为1.2 mm，导热系数仅为0.2 W/(m·K)，属于热不良导体，故其对器件温升的影响可忽略。

为更加全面的验证所提模型及参数提取方法的有效性，还选取了市面上常见的两种铝型材散热器加装在功率器件上。散热器型号分别为YA25 和YB30，相应有效散热面积分别为40 cm2和79 cm2，结构尺寸如图4所示。

为了保证实验的可重复性，准确分析模型参数变化规律，实验电路板被安置在50 cm ×60 cm ×70 cm的恒温箱中。

图4 实验用散热器结构尺寸示意图Fig.4 The structure of experimental heat sinks

4 结果分析与讨论

4.1 实验结果分析

在不同电流等级下，分别对不加装和加装散热器的功率器件进行多次温升实验。

以无散热器的功率器件实验结果为例，说明器件温升的热动态过程。如图5所示，当器件导通后，工作温度首先迅速升高，随着时间的增加，温升速率下降，温度逐渐进入稳态。电流等级的提高可明显提高器件稳态温度。加装散热器后的器件温升动态过程与无散热器时基本一致，只是同等电流条件下的稳态温度较低，不再赘述。

图5 功率器件温升曲线图Fig.5 Measured temperature curves of the power device

根据热工测量理论［23］，物体受热后，温度由初值升高至终值的63.2%所用的时间被定义为热时间常数，而被测物体热时间常数通常应大于温度探头热时间常数，才能有效反映物体温升动态过程。利用实验结果，可得不同散热器条件下的功率器件温升平均热时间常数τ，如表3 所示。表中参数k 为功率器件热时间常数与温度探头热时间常数的比值。容易发现，功率器件在无散热器、加装散热器YA25 和加装散热器YB30 三种情况下，其热时间常数分别约为温度探头热时间常数的14.8、25.7 及29.2 倍。这表明实验中采用的MF52 温度探头满足工程测量的动态响应要求。

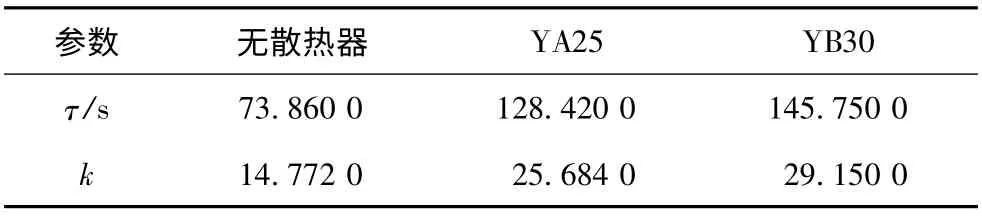
表3 不同散热条件下功率器件温升曲线的热时间常数Tab.3 Thermal time constant of power device temperature curves with different heat sinks

相关实验结果还可表明，功率器件的温升动态过程与电容充电的动态过程极为相似，故文献［13］利用一阶系统时域响应公式对器件温升曲线进行了拟合，得到了器件不同状态下温度随时间的变化关系。而文献［14］则对温升曲线建立状态观测模型，以实现器件温度的预测。显然，这类模型并不关注器件热参数，也无法描述不同电流和散热器规格对热参数的影响，只能描述已有实验温升曲线后的器件热动态过程，因此具有一定局限性。

4.2 器件热参数辨识及规律分析

以式(4)为目标函数对实验结果进行辨识，得到不同电流及不同散热器条件下的功率器件热路参数如表4 所示。

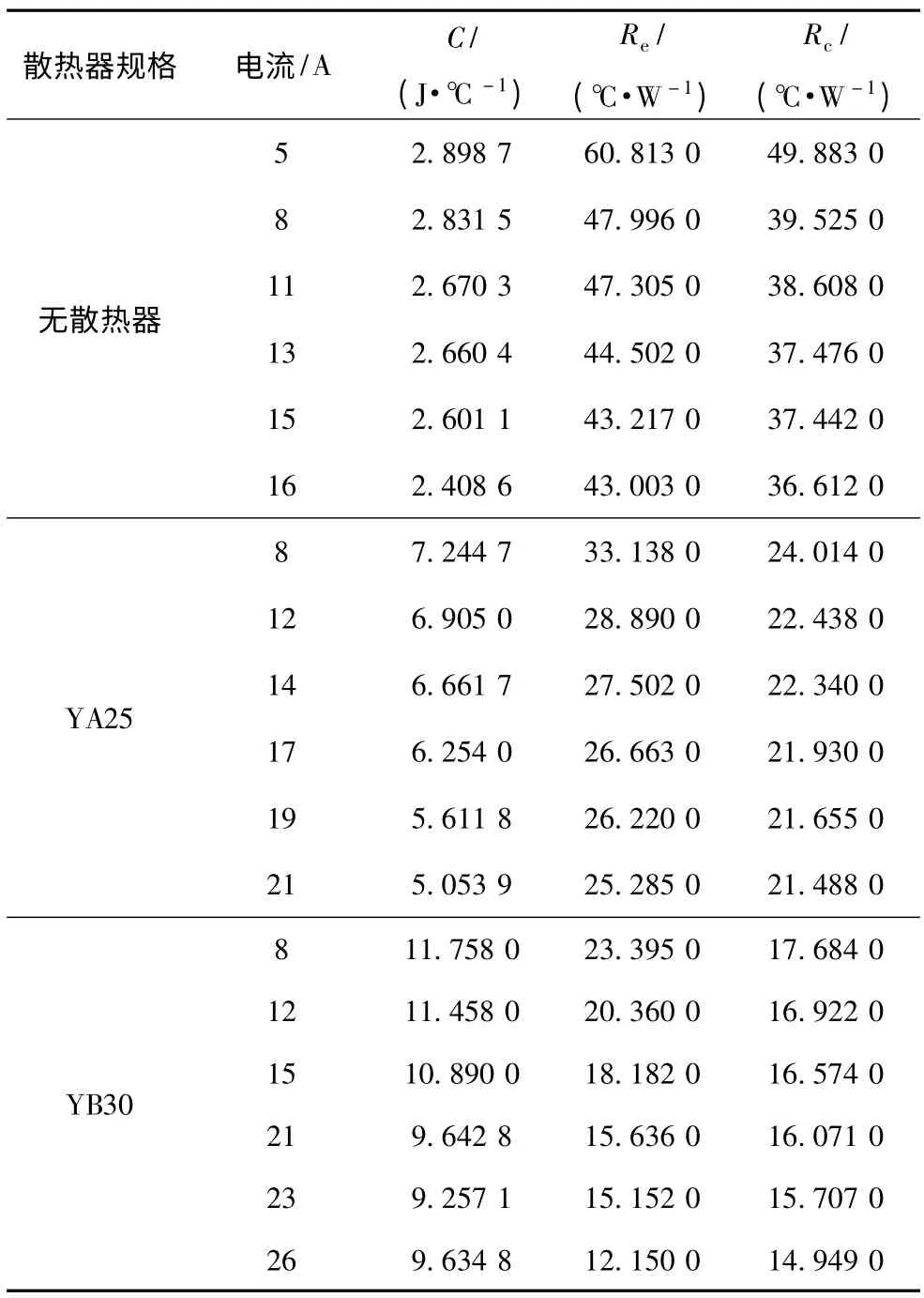
表4 功率器件集总参数热路模型的参数辨识结果Tab.4 Parameter identification results of the thermal circuit model of power device

分析表4 可见，当散热器规格确定后，功率器件热路参数与导通电流有关。根据传热学，环境与器件的温差增大时，器件周围空气流动加强，利于散热。另外，热辐射会随着器件温度的升高而增强，同样强化散热。因此，环境热阻应随电流等级的升高而减小。Re的参数辨识结果与该规律相符，验证了温升模型的有效性。等效热容C 与等效热阻Rc等参数受到器件各层材料之间的接触热阻影响，缺乏理论分析方法。但辨识结果表明，随着电流等级的提高，C 和Rc亦呈减小趋势。

散热器规格对器件热路参数影响同样明显。密度相同的散热器，质量随有效散热面积的增加而增大，故功率器件加装YA25 及YB30时等效热容较大，无散热器时等效热容较小。辨识结果还表明，Re和Rc随散热面积的增加呈减小趋势，这说明安装较大的散热器不仅可增加环境的对流散热能力，也可增加器件与电路板之间的热交换能力。

为量化热路参数变化规律，采用式(6)所示的多项式对热路参数辨识结果进行拟合

式中:x 为热路参数;n 为多项式阶次;ai为多项式系数;I 为导通电流。

拟合表明，多项式阶次选择3 阶，拟合误差在5%之内，具有较高精度。表5 为拟合所得的多项式系数表。

表5 多项式拟合系数表Tab.5 The coefficients of polynomial fitting results

4.3 模型精度分析

将参数变化的拟合结果代入热路模型中，并求解模型响应，可计算出功率器件的温升过程。图6分别为不同散热器和电流等级条件下，模型计算结果与实验结果对比的相对误差曲线。表6 则列出了对应的平均相对误差(Average Relative Error，ARE)。分析表明，在得到了模型参数变化规律的条件下，所提热路模型最大计算误差小于5%，平均计算误差小于2%，具有较高精度，能准确反映功率器件温升动态过程。

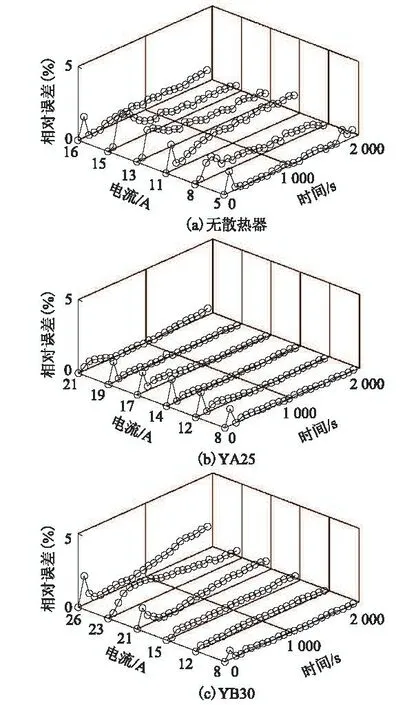
图6 不同散热器及电流条件下模型计算结果误差曲线Fig.6 Calculated error results of the model with different current and heat sinks

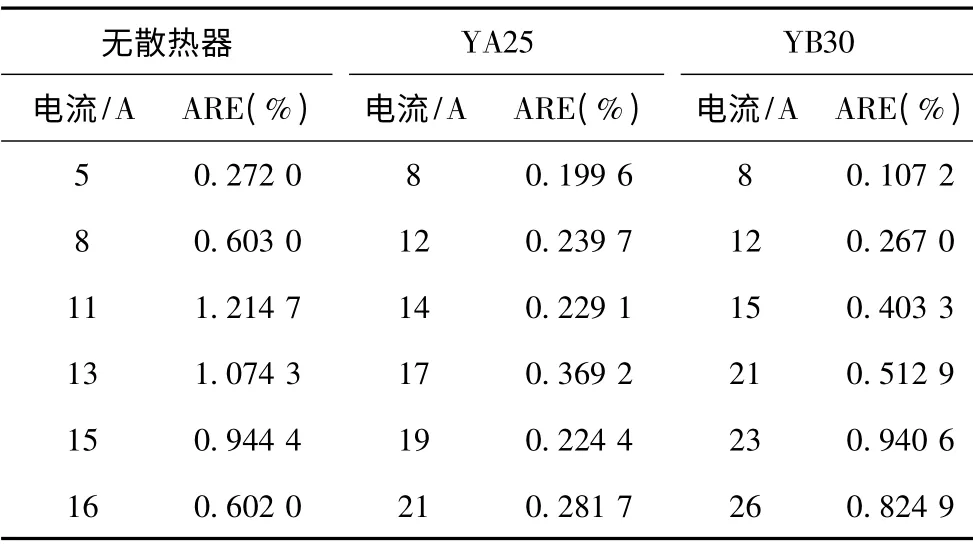
表6 不同散热器及电流条件下功率器件温升计算结果平均相对误差Tab.6 The ARE of measured and calculated temperature rise with different current and heat sinks

为了验证参数变化规律拟合的正确性，针对加装不同规格散热器的功率器件，随机增补了若干实验。这些实验的电流值及温升实验数据均未参与式(6)的拟合。利用模型对增补实验进行计算，得到相应计算误差曲线如图7所示。图7表明此时计算结果误差同样较小，满足工程计算要求。这也表明，在获得模型参数变化规律的基础上，即使未知功率器件的实验温升曲线，本文模型也能准确计算器件热动态过程，故能够克服传统集总参数温升模型建立在实验温升曲线上的不足。

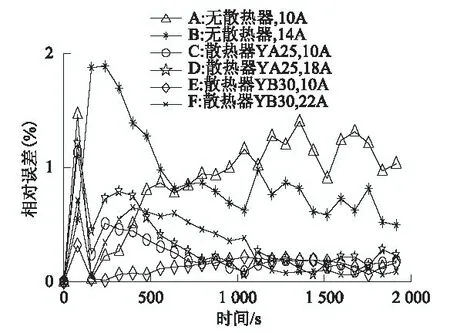
图7 增补实验的模型计算结果误差曲线Fig.7 Calculated error curves of additional experiments

另外，模型参数变化规律可离线获得。这意味着在实际使用中，即使功率器件上不装设温度传感器，其温升过程也可通过软件方式进行计算。因此，所提模型能够避免温度探头脱落和红外测温精度不足等弊端，提高功率器件使用过程中温度获取的可靠性，尤其适合在传感器固定困难和精度易发生漂移的场合中使用。

5 结论

本文将功率器件及散热器作为一个整体，通过热路方法建立了集总参数模型。利用遗传算法对模型参数进行了辨识，所得结论如下:

1)参数辨识方法能有效提取功率器件集总模型热路参数、克服等效热路参数难以确定的问题，辨识结果亦可揭示模型参数随电流等级及散热器规格变化的规律。

2)在获得模型参数变化规律后，即便未知功率器件的实验温升曲线，所提模型也能准确计算器件热动态过程，能够克服传统集总参数温升模型建立在实验温升曲线基础上的不足。

3)模型参数变化规律可离线获得，即使功率器件上不装设温度传感器，其温升过程也可通过所提模型进行计算，减少了对温度传感器的依赖，有助于提高功率器件使用过程中温度获取的可靠性。

4)实际工程中，功率器件的通断存在PWM 控制、SPWM 控制以及SVPWM 控制等多种控制方式，故其导通电流并非恒定值，且上述控制方式中的占空比计算又与整个功率电子设备的控制方式(如功率电源中的电压电流双闭环控制以及电动机调速中的电压转速双闭环控制等方式)有关，因此未来将在现有工作基础上，研究等效热路参数随开关频率和占空比变化的规律，进一步完善集总参数热路模型。

［1］ Ciappa M．Selected failure mechanisms of modern power modules［J］．Microelectronics Reliability，2002，42(4-5):653-667．

［2］ 唐勇，汪波，陈明，等．高温下的IGBT 可靠性与在线评估［J］．电工技术学报，2014，29(6):17-23．

Tang Yong，Wang Bo，Chen Ming，et al．Reliability and on-line evaluation of IGBT modules under high temperature［J］．Transactions of China Electrotechnical Society，2014，29(6):17-23．

［3］ Murdock D A，Torres J E R，Connors J J，et al．Active thermal control of power electronic modules［J］．IEEE Transactions on Industry Applications，2006，42(2):552-558．

［4］ Andresen M，Liserre M．Impact of active thermal management on power electronics design［J］．Microelectronics Reliability，2014，54(9-10):1935-1939．

［5］ Blasko V，Lukaszewski R，Sladky R．On line thermal model and thermal management strategy of a three phase voltage source inverter［C］．Conference Record of the 1999 IEEE Industry Applications Conference，Phoenix，AZ，1999，2:1423-1431．

［6］ Szabo P，Steffens O，Lenz M，et al．Transient junctionto-case thermal resistance measurement methodology of high accuracy and high repeatability［J］．IEEE Transactions on Components and Packaging Technologies，2005，28(4):630-636．

［7］ Ammous A，Ghedira S，Allard B，et al．Choosing a thermal model for electrothermal simulation of power semiconductor devices［J］．IEEE Transactions on Power Electronics，1999，14(2):300-307．

［8］ Ciappa M，Fichtner W，Kojima T，et al．Extraction of accurate thermal compact models for fast electro-thermal simulation of IGBT modules in hybrid electric vehicles［J］．Microelectronics Reliability，2005，45(9-11):1694-1699．

［9］ 陈明，胡安，唐勇，等．绝缘栅双极型晶体管传热模型建模分析［J］．高电压技术，2011，37(2):453-459．

Chen Ming，Hu An，Tang Yong，et al．Modeling analysis of IGBT thermal model［J］．High Voltage Engineering，2011，37(2):453-459．

［10］ Pandya K I，McDaniel W．A simplified method of generating thermal models for power MOSFETs［C］．Eighteenth Annual IEEE Symposium Semiconductor Thermal Measurement and Management，San Jose，USA，2002:83-87．

［11］ Chen M C，Yu Feixia，Jun Lin，et al．Steady-state and dynamic thermal models for heat flow analysis of silicon-on-insulator MOSFETs［J］．Microelectronics Reliability，2004，44(3):381-396．

［12］ 晏敏，彭楚武，颜永红，等．红外测温原理及误差分析［J］．湖南大学学报(自然科学版)，2004，31(5):110-112．

Yan Min，Peng Chuwu，Yan Yonghong，et al．Principle and error analysis of infra-red temperature measurement［J］．Journal of Hunan University(Natural Sciences)，2004，31(5):110-112．

［13］ 李洪才，陈非凡，董永贵．功率器件散热特性的非稳态测量方法［J］．电工技术学报，2012，27(2):114-120．

Li Hongcai，Chen Feifan，Dong Yonggui．An unsteadystate measurement method for charactering heat dissipation properties of power electronic devices［J］．Transactions of China Electrotechnical Society，2012，27(2):114-120．

［14］ 金雍，羊彦，毕强．功率半导体器件温度状态的实时预测技术［J］．电工技术学报，2001，16(5):68-72．

Jin Yong，Yang Yan，Bi Qiang．The technique of predicating the running state of power semiconductor units in real time［J］．Transactions of China Electrotechnical Society，2001，16(5):68-72．

［15］ 魏克新，杜明星．基于集总参数法的IGBT 模块温度预测模型［J］．电工技术学报，2011，26(12):79-84．

Wei Kexin，Du Mingxing．Temperature prediction model of IGBT modules based on lumped parameters method［J］．Transactions of China Electrotechnical Society，2011，26(12):79-84．

［16］ Kraus R，Mattausch H J．Status and trends of power semiconductor device models for circuit simulation［J］．IEEE Transactions on Power Electronic，1998，13(3):452-465．

［17］ 刘海霞，蒋鹞飞，宋凝芳，等．基于热电类比法的光纤陀螺环模块热分析［J］．北京航空航天大学学报，2014，40(5):596-601．

Liu Haixia，Jiang Yaofei，Song Ningfang，et al．FOG ring modules thermal analysis based on thermoelectric analogy［J］．Journal of Beijing University of Aeronautics and Astronautics，2014，40(5):596-601．

［18］ Swift G，Molinski T S，Lehn W．A fundamental approach to transformer thermal modeling partⅠ:theory and equivalent circuit［J］．IEEE Transactions on Power Delivery，2001，16(2):171-175．

［19］ 刘刚，阮班义，林杰，等．架空导线动态增容的热路法稳态模型［J］．高电压技术，2013，39(5):1107-1113．

Liu Gang，Ruan Banyi，Lin Jie，et al．Steady-state model of thermal circuit method for dynamic overhead lines rating［J］．High Voltage Engineering，2013，39(5):1107-1113．

［20］ 胡建辉，李锦庚，邹继斌，等．变频器中的IGBT 模块损耗计算及散热系统设计［J］．电工技术学报，2009，24(3):159-163．

Hu Jianhui，Li Jingeng，Zou Jibin，et al．Losses calculation of IGBT module and heat dissipation system design of inverters［J］．Transactions of China Electrotechnical Society，2009，24(3):159-163．

［21］ 刘长良，于希宁，姚万业，等．基于遗传算法的火电厂热工程模型辨识［J］．中国电机工程学报，2003，23(3):170-174．

Liu Changliang，Yu Xining，Yao Wanye，et al．Model identification of power plant thermal process based on genetic algorithm［J］．Proceedings of the CSEE，2003，23(3):170-174．

［22］ Leite J V，Avila S L，Batistela N J，et al．Real coded genetic algorithm for Jiles-Atherton model parameters identification［J］．IEEE Transactions on Magnetics，2004，40(2):888-891．

［23］ 张尧，周鑫，牛海清，等．单芯电缆热时间常数的理论计算与试验研究［J］．高电压技术，2009，35(11):2801-2806．

Zhang Yao，Zhou Xin，Niu Haiqing，et al．Theoretical calculation and experimental research on thermal time constant of single-core cables［J］．High Voltage Engineering，2009，35(11):2801-2806．