矩阵变换器间接空间矢量过调制策略分析与研究
夏益辉 乔鸣忠 张晓锋 魏永清
(海军工程大学电气工程学院 武汉 430033)
0 引言
与传统交-直-交变频器相比,矩阵变换器具有以下优点[1]:①可以实现输出、输入电流的正弦控制;②输入功率因数可调,可用于无功功率补偿;③能量可双向流动,节约能源;④不需要直流储能环节,功率密度高。
随着未来对能源利用效率和网侧电能质量要求不断提高,矩阵变换器是目前很有前景的电力变换装置。为此,很多专家学者对其进行了研究和探索,并取得了丰硕的成果,主要体现在输入滤波器设计[2]、换流方法[3,4]、系统稳定性分析[5]、输出共模电压抑制[6,7]、调制策略[8,9]和电压传输比[10-18]等方面。
传统空间矢量调制在线性区域电压传输比最大为0.866,在满磁调速时,电压传输比低会导致调速范围低,电动机带载能力弱;在弱磁调速时,电动机虽然可工作在额定转速,但会增加电动机损耗。因此,提高电压传输比成为很多专家学者研究的一个课题。传统变频器空间矢量调制与矩阵变换器存在一种等价关系,使得在传统变频器中获得的基于空间矢量调制的策略均适用于矩阵变换器间接空间矢量调制,文献[10-12]将传统基于双模模式下的空间矢量过调制用于矩阵变换器过调制中,有效提高了电压传输比,但该方法需要较大的存储空间,计算量大且输出电压谐波含量高。文献[13]同样采用双模过调制模式,将矩阵变换器电压调制比提高到1,同时对输出电压谐波特性进行了分析。文献[14]将双模过调制模式用于双级矩阵变换器,并进行了仿真研究和实验分析。文献[15]对直接空间矢量过调制方法进行了分析,指出通过放弃使用零矢量和校正参考输出电压矢量角度可提高电压传输比,同时对输入电流进行了分析,但该方法存在输出电压谐波含量高且运算量大的缺点。文献[16]利用圆形矢量和基本矢量,提出一种基于电压基波幅值线性化过调制计算方法,有效提高了输出电压传输比,且易于数字化实现,但输出电压谐波含量偏高。文献[17]对矩阵变换器驱动电动机过调制区域转矩纹波产生的原因及特性进行了分析,并提出采用BF(beat-free)控制进行抑制,获得了较好的效果。文献[18]将过调制区域分为两部分,针对不同区域采用不同的矢量组合,提出基于多轨迹矢量加权的过调制方法,相比于传统的单模和双模过调制策略,该方法原理简单,易于数字化实现,输出电压谐波含量低,但六边形矢量和基本矢量存在选取不尽合理的问题。以上文献基本都是从间接空间矢量逆变级过调制方法入手来提高电压传输比,但当输入电流沿六边形矢量旋转时,此时实际输出电压与期望输出电压之间误差较大,且输入电流谐波含量高,很少有文献从整流级和逆变级对矩阵变换器间接空间矢量过调制方法协调设计,即将电压传输比、输入电流和输出电压谐波同时进行考虑。
本文首先对矩阵变换器拓扑结构及间接空间矢量调制原理进行了介绍;其次,对基于多轨迹矢量加权过调制(在本文此后将其称为传统过调制策略)的基本原理进行了分析,对六边形矢量和基本矢量对输出电压基波幅值和输出电压谐波含量的影响进行了探讨;再次,从整流级和逆变级入手,对其调制策略同时进行了改进,提出一种新的基于间接空间矢量调制的过调制策略;最后,对改进前后的过调制策略对矩阵变换器输入和输出性能的影响进行了仿真研究与实验验证。
1 矩阵变换器拓扑结构及间接空间矢量调制原理
1.1 矩阵变换器基本结构
图1为三相输入-三相输出直接型矩阵变换器结构,由输入滤波器、双向流动的开关管和钳位电路组成。输入滤波器用于滤除高频谐波,钳位电路用于防止电压突变对系统造成冲击,双向开关管用于合成期望的输出电压和输入电流。
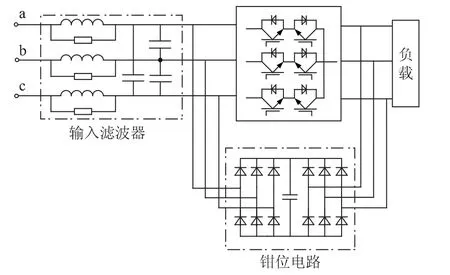
图1 矩阵变换器基本结构Fig.1 The basic structure of matrix converter
1.2 间接空间矢量调制原理
间接空间矢量是将矩阵变换器等价于一交-直-交结构,输入侧为整流,输出侧为逆变,其等效的结构如图2所示。图中Sjk为开关矩阵变量,j∈{a,b,c,A,B,C},k∈{p,n}。在此基础上对虚拟整流部分和虚拟逆变部分分别进行空间矢量调制。

图2 矩阵变换器等效为虚拟交-直-交的结构Fig.2 Fictitious AC-DC-AC structure of matrix converter
图3为输入电流扇区划分,用于合成虚拟直流电压。由图可知,输入电流由6 个扇区组成,针对输入电流矢量位于不同扇区时,采用不同的基本矢量Ix组合来进行合成,x 为扇区1~6。Isin和Ihex分别为最大内切圆矢量和六边形矢量。
图4为输出电压扇区划分,由6 个扇区组成,针对输出电压矢量位于不同扇区,采用不同的基本矢量Ux组合来进行合成,x 为扇区1~6。Usin和Uhex为最大内切圆矢量和六边形矢量。
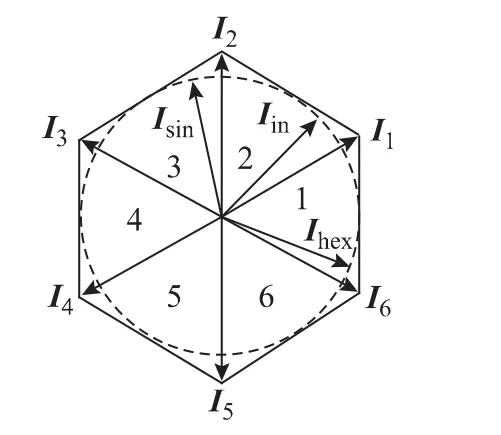
图3 输入电流矢量和扇区Fig.3 Six input current vectors and sectors
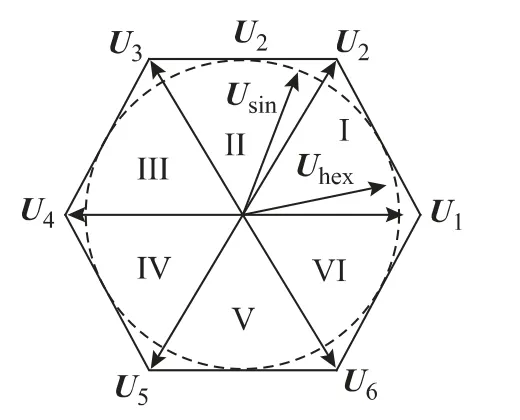
图4 输出电压矢量和扇区Fig.4 Six output voltage vectors and sectors
2 传统过调制策略原理及六边形矢量和基本矢量对其过调制性能的影响
2.1 传统过调制原理[18]
在整流级,即输入侧,输入电流矢量沿六边形旋转,即

在逆变级采用多轨迹矢量加权过调制方法,将过调制分为两个区间,即过调制Ⅰ区(0.866 <M ≤0.909)和过调制Ⅱ区(0.909 <M≤1)。
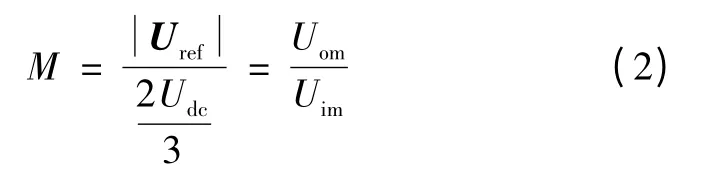
式中Uref为参考电压矢量。
过调制Ⅰ区:0.866 <M≤0.909,定义变量k 为
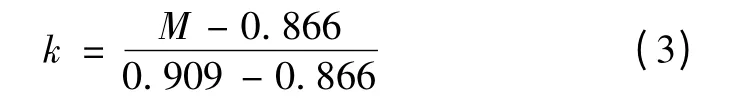
参考电压矢量Uref可表示为圆形矢量和六边形矢量之和,即

过调制Ⅱ区:0.909 <M≤1,变量k 定义为
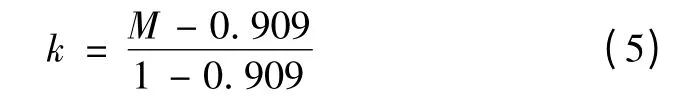
参考输出电压矢量Uref由六边形矢量Uhex和基本矢量Ux(Ux+1)合成,即
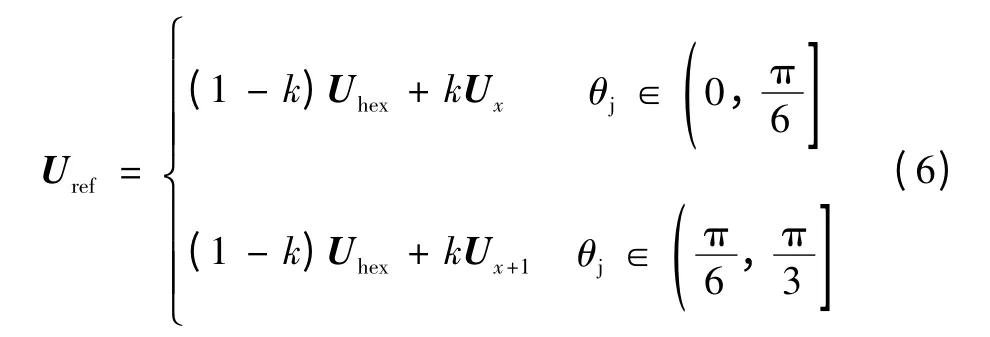
2.2 六边形矢量对过调制性能的影响
由式(4)可知,此时输出电压基波幅值为
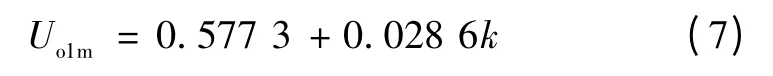
输出电压谐波畸变率为

图5为输出电压谐波含量随变量k 的变化曲线。由图可知,随着k 的增加,输出电压谐波畸变率同样会逐渐增大。由式(7)可知,随着k 的增加,输出电压基波幅值会逐渐增大。由此可进一步得出在由圆形矢量和六边形矢量合成的参考电压矢量中,增大圆形矢量在参考电压矢量中的权重(1 -k),即减小k,输出电压基波幅值和谐波含量将会减小。圆形矢量的输出电压基波有效值和输出电压有效值相等,使得圆形矢量对输出电压谐波含量的贡献为零,而其只对输出电压基波幅值有影响。
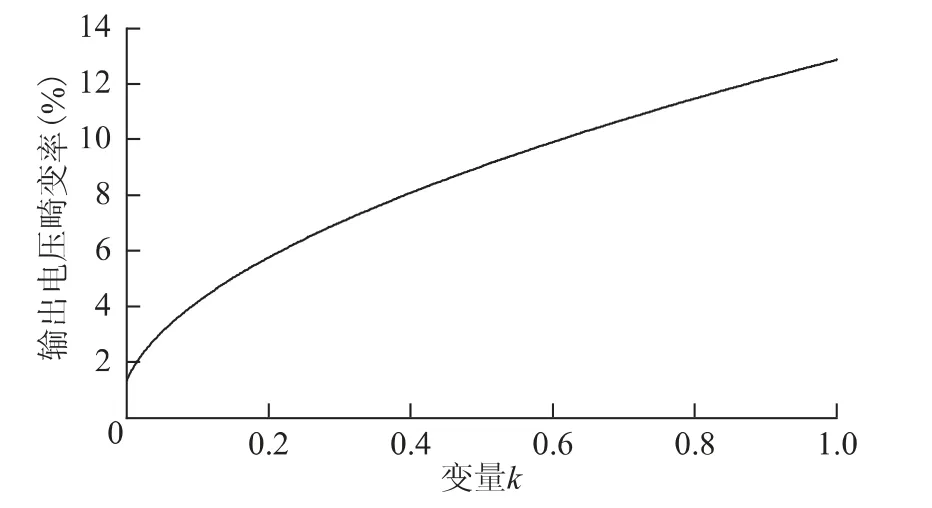
图5 输出电压谐波畸变率随k 变化曲线Fig.5 Curve of output voltage THD varied with k
同理,可以对基本矢量对输出电压基波幅值和输出电压谐波畸变率的影响进行分析,其与六边形矢量对输出电压性能影响结果一致,这里不再详细论述。
3 一种新的矩阵变换器间接空间矢量过调制方法
3.1 整流级改进调制原理
将输入电流矢量分为两部分,一部分由圆形矢量合成,另一部分由六边形矢量合成。当M=0.866时,参考电流矢量不需要使用六边形矢量,而当M=1时,参考电流矢量必须沿六边形矢量旋转,这里将六边形矢量在参考电流矢量中的权重简单的线性化设计,具体如下
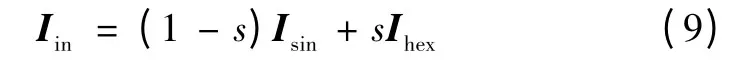
假定输入电流矢量位于扇区2,则相邻两矢量I1和I2的作用时间dα和dβ计算如下
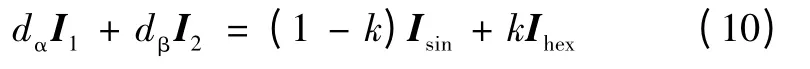
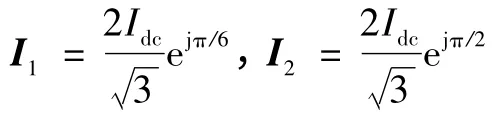
式中,将其代入式(9)可得
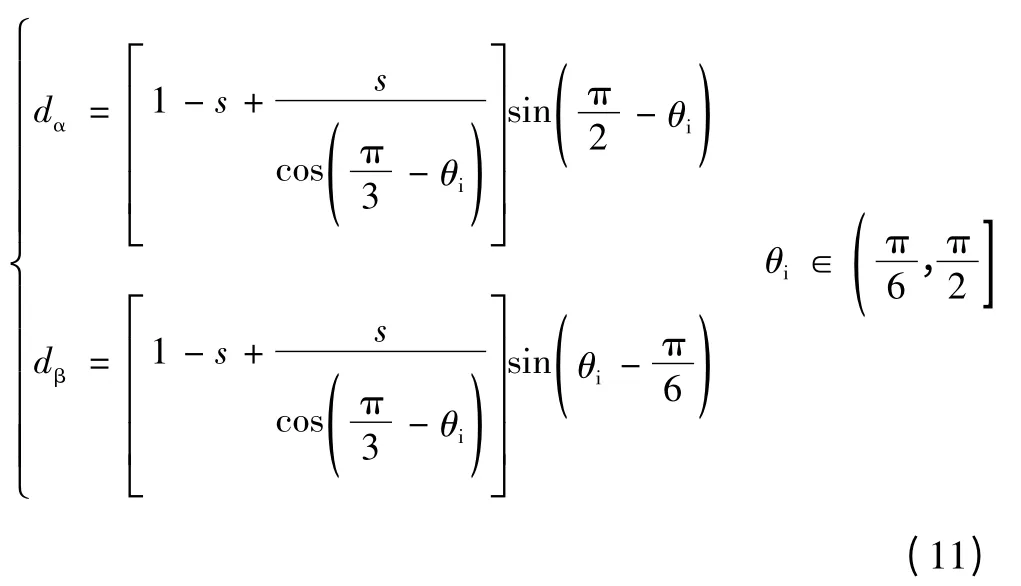
3.2 逆变级改进过调制原理
逆变级同样将过调制分为两个区域:过调制区域Ⅰ(0.866 <M≤0.909)和过调制区域Ⅱ(0.909 <M≤1)。
过调制区域Ⅰ,变量k 定义为
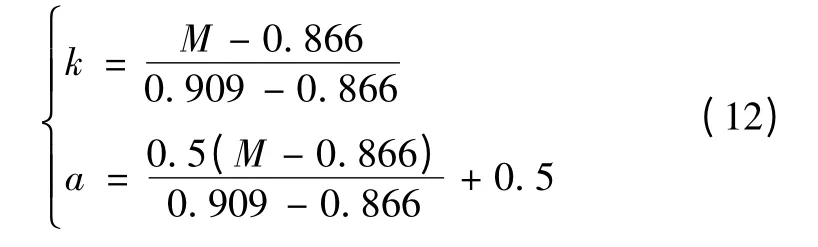
参考电压矢量Uref可表示为圆形矢量Usin和基本矢量Ux(Ux+1)之和,即
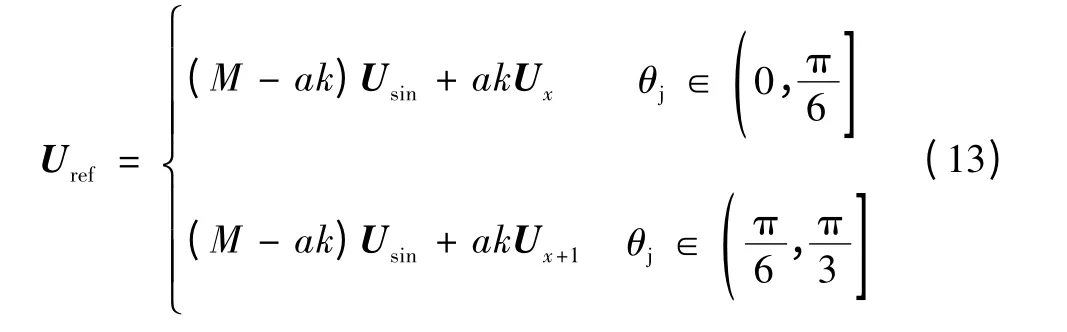
假定参考输出电压矢量位于扇区1,则相邻两矢量U1、U2的作用时间dm、dn分别为代入式(14),可求得dm和dn分别为
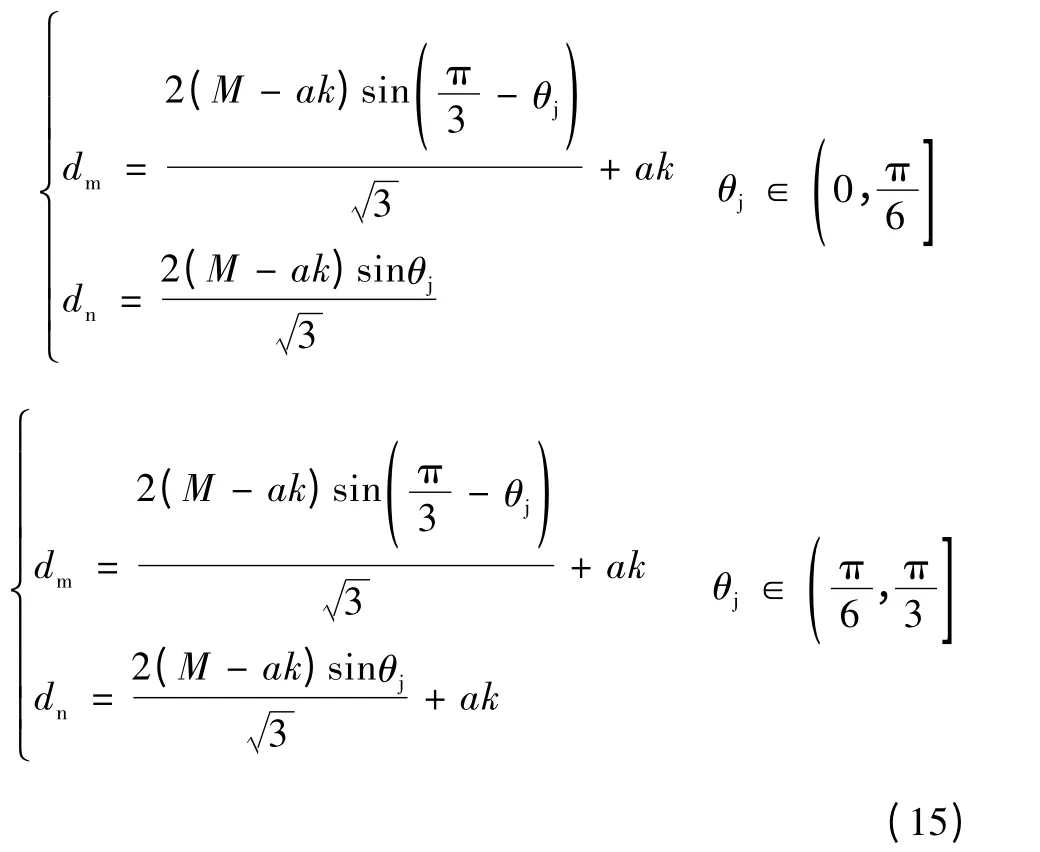
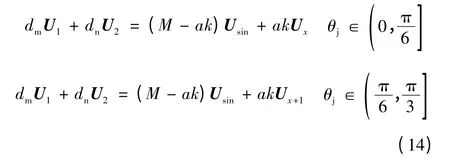

过调制区域Ⅱ,变量k 定义为

调整后的参考电压矢量Uref为
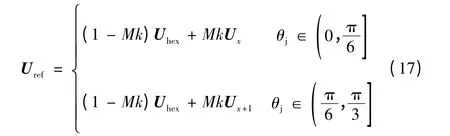
假定参考输出电压矢量位于扇区1,则相邻两矢量U1、U2的作用时间dm、dn分别为

求解式(18),得相邻两矢量作用时间为
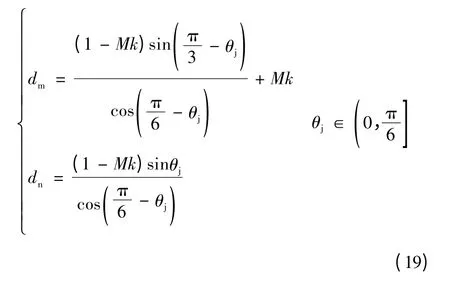

综上所述,与传统多轨迹矢量加权过调制方法相比,本文所提过调制方法在整流级和逆变级同时对参考电流矢量和参考电压矢量的矢量组成及权重进行了设计,在保证输出电压跟踪期望电压的前提下,尽可能减小六边形矢量和基本矢量在参考矢量中的权重,由2.2 节分析可知,输出电压和输入电流谐波含量将会有效降低。
4 仿真研究与实验验证
下面将针对传统过调制策略(整流级输入电流矢量沿六边形旋转,逆变级采用传统多轨迹矢量加权策略)、逆变级改进过调制策略(整流级输入电流矢量仍然沿六边形旋转,逆变级采用3.2 节改进过调制策略)和整流级与逆变级同时改进过调制策略(整流级采用3.1 节调制方法,逆变级采用3.2 节改进过调制策略)之间的过调制性能进行对比研究。
4.1 仿真研究
利用Matlab 软件搭建了直接型矩阵变换器的仿真模型,参数设置见表1。

表1 矩阵变换器参数Tab.1 Matrix converter parameters
图6~图8分别为3 种不同过调制策略下输出电压基波幅值、输出相电流以及输入相电流与调制比之间的关系。其中,输出线电压谐波畸变率为输出线电压经一截止频率160 Hz 低通滤波器后得到。
由图6可知,采用本文所提过调制策略时,输出电压与参考电压之间的误差最小,这是由于在输入级减小了六边形矢量的使用,而在逆变级在不同扇区减小了六边形矢量和基本矢量,只对逆变级进行改进时输出电压与参考电压误差有所减小。说明减小六边形矢量和基本矢量的作用时间,可减小输出电压基波幅值。
由图7、图8可看出,相比于传统过调制策略,只对逆变级进行改进时,输出相电流谐波含量有所减小,而输入相电流谐波在低调制比时明显减小,在高调制比时两者输入相电流谐波含量相差不大;在对整流级和逆变级同时进行改进时,输出相电流谐波略微减小,而输入相电流谐波含量减小显著,说明对整流级进行改进,可有效降低输入电流谐波含量。仿真结果与理论分析一致,表明本文所提新的基于间接空间矢量调制的过调制策略是正确可行的。
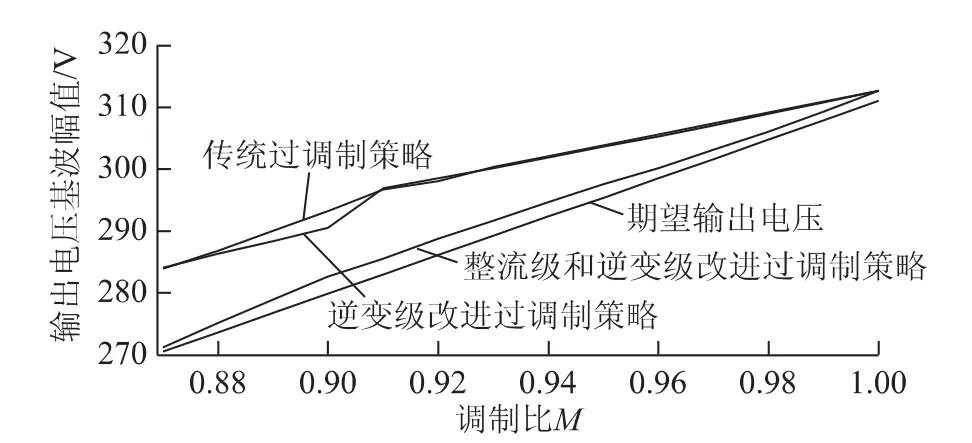
图6 输出电压基波幅值与调制比M 之间的关系Fig.6 The relation between output voltage Uo1mand index M

图7 输出相电流谐波畸变率与调制比之间的关系Fig.7 The relation between output voltage and output current THD and index M
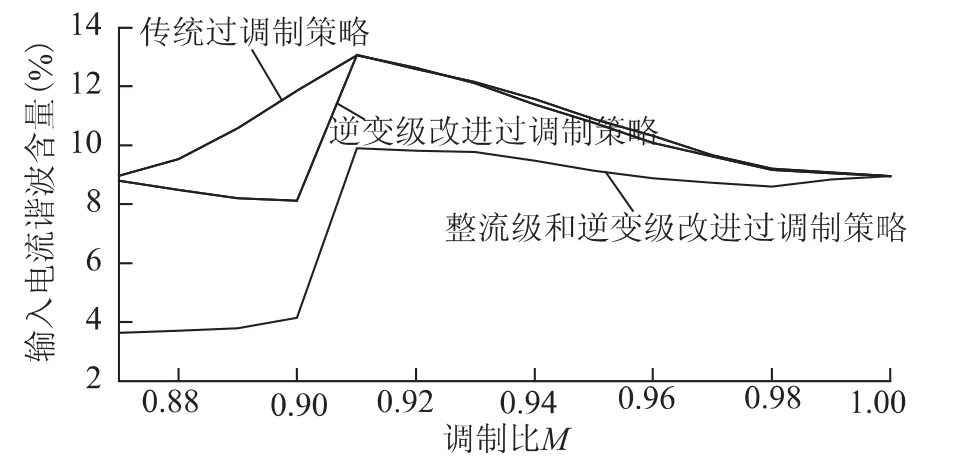
图8 输入相电流谐波畸变率与调制比之间的关系Fig.8 The relation between input current THD and index M
4.2 实验验证
在实验室搭建一基于DSP+FPGA 的5 kW 矩阵变换器样机进行实验验证,如图9所示。实验参数与仿真参数一致。
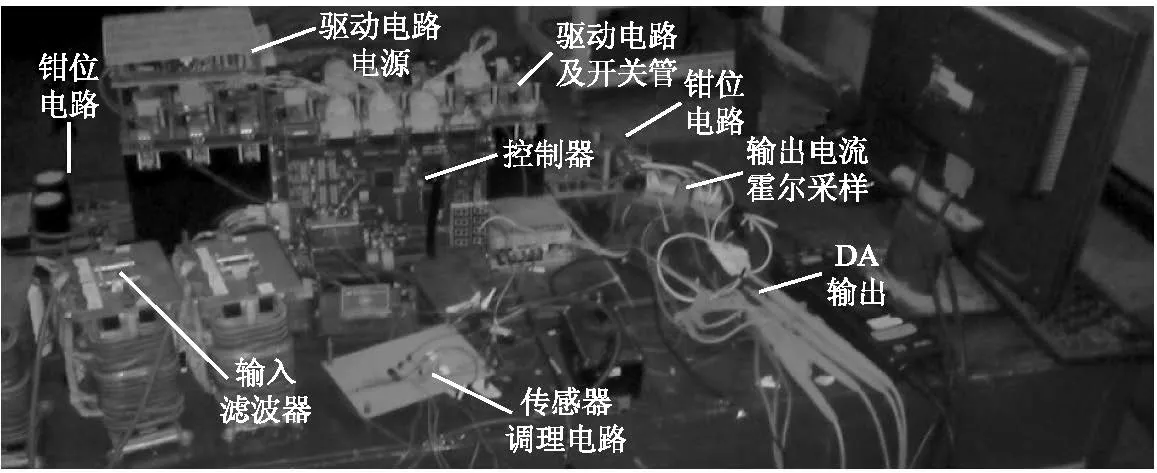
图9 矩阵变换器实验系统Fig.9 The experimental platform of matrix converter
图10、图11是调制比分别为0.88 和0.92时采用传统过调制策略(策略一)、逆变级改进过调制策略(策略二)和本文所提整流级和逆变级同时改进过调制策略(策略三)下输出线电压、相电流和输入相电流波形。表2 为调制比分别为0.88 和0.92时采用3 种过调制策略输出电压误差、输入和输出电流谐波畸变率实验结果。
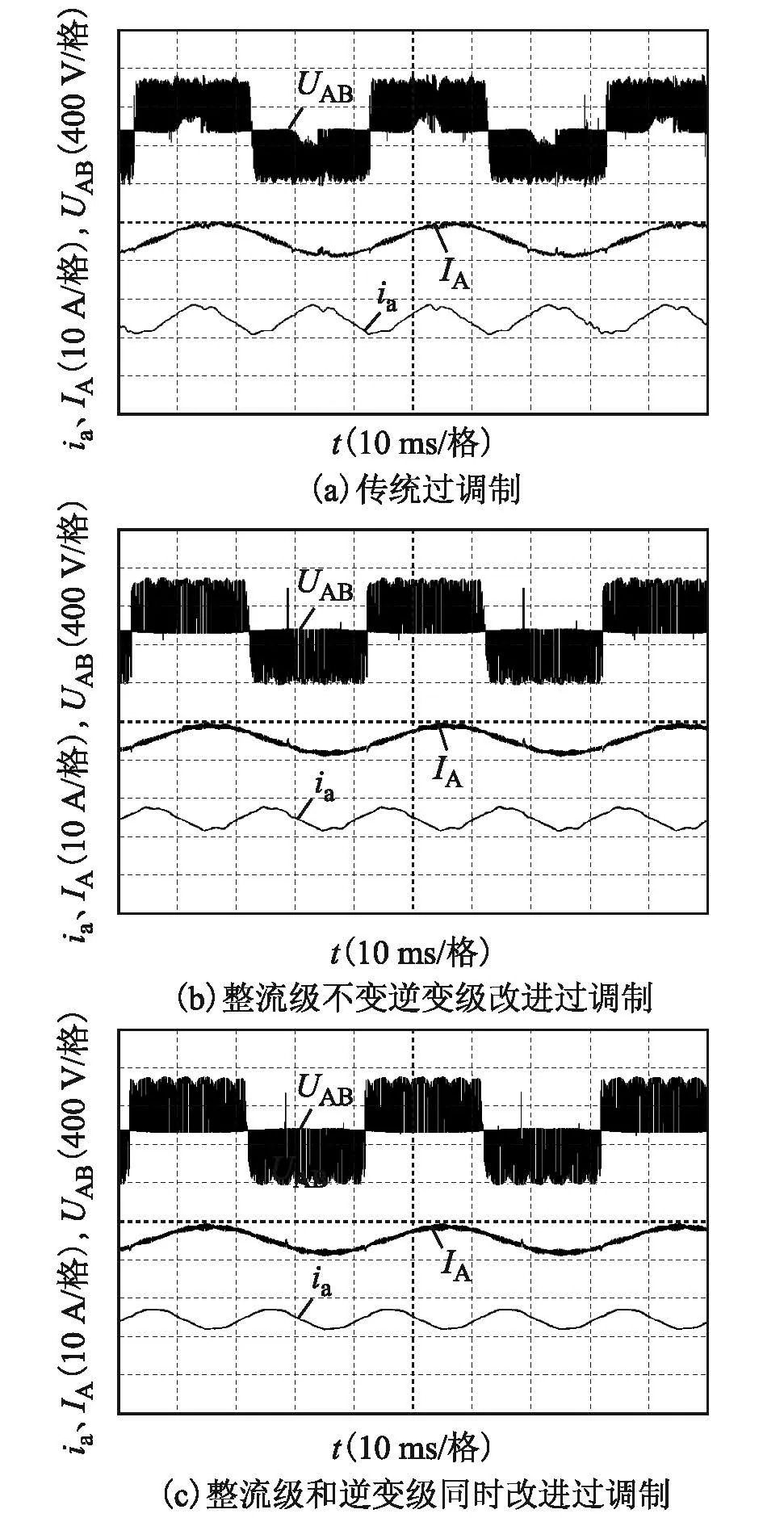
图10 不同过调制策略下调制比为0.88时输出输入波形Fig.10 The waveforms of output and input with different over-modulation strategies under M 0.88

图11 不同过调制策略下调制比为0.92时输出输入波形Fig.11 The waveforms of output and input with different over-modulation strategies under M 0.92
由图10和图11也可看出,相比于传统过调制策略,只对逆变级进行改进时,输出和输入电流波形质量在低调制比时有所提高,但高调制比变化不大。而采用本文所提整流级和逆变级同时改进过调制策略时,输出电流和输入电流波形质量明显提高,特别是在过调制区域Ⅰ。由表2 可知,所提整流级和逆变级同时改进过调制策略具有最小的输出电压与参考电压误差。实验结果与理论分析和仿真结果一致,证明理论分析是正确的和本文所提过调制策略是切实可行的。
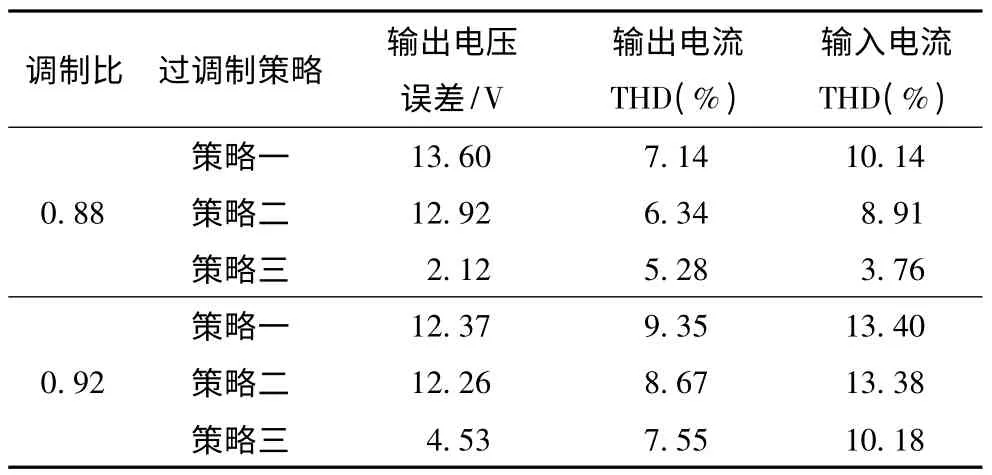
表2 不同过调制策略下输入输出变量数据Tab.2 Experimental data of input and output parameters with different over-modulation strategies
5 结论
针对传统过调制策略输出电压与参考电压误差大和输入电流谐波含量高的缺点,利用间接空间矢量调制特点,提出了逆变级改进和整流级与逆变级同时改进的两种过调制策略。仿真结果表明,本文所提整流级和逆变级同时改进过调制方法具有最小的输出电压误差和输入相电流谐波含量,实验结果证明理论分析是正确的和本文所提过调制方法是可行的。
[1] 孙凯,周大宁,梅杨,等.矩阵式变换器技术及其应用[M].北京:机械工业出版社,2007.
[2] Andrew T,Pericle Z,Jon C,et al.Automated optimal design of input filters for direct AC/AC matrix converter[J].IEEE Transactions on Industrial Electronics,2012,59(7):2811-2823.
[3] Liu Xiao,Zhang Qianfeng,Hou Dianli.Research of one-step commutation strategy in matrix converter[J].Advanced Materials Research,2012(516):1804-1807.
[4] She H W,Lin H,He B,et al.Implementation of voltage-based commutation in space-vector-modulated matrix converter[J].IEEE Transactions on Industry Electronics,2012,59(1):154-166.
[5] Sun Y,Su M,Li X,et al.A general constructive approach to matrix converter stabilization[J].IEEE Transactions on Power Electronics,2013,28(1):418-431.
[6] Jordi E,Carlos O,Liliana D L,et al.Reduction of output common mode voltage using a novel SVM implementation in matrix converters for improved motor lifetime[J].IEEE Transactions on Industrial Electronics,2014,61(11):5903-5911.
[7] Ju H C,Enjeti P N.An approach to reduction commonmode voltage in matrix converter[J].IEEE Transactions on Industrial Application,2003,39(4):1151-1159.
[8] Casadei D,Serra G,Tani A.Matrix converter modulation strategy:a new general approach based on space-vector representation of the switch state[J].IEEE Transactions on Industrial Electronics,2002,49(2):370-381.
[9] Tuyen D,Li H H.A new SVM method for an indirect matrix converter with common-mode voltage reduction[J].IEEE Transactions on Industrial Electronics,2014,10(1):61-72.
[10] Itoh J I,Koiwa K,Kato K.Input current stabilization control of a matrix converter with boost-up functionality[C].International Power Electronics Conference,Sapporo,Japan,2010:2708-2714.
[11] Kerman R J,Seibej B J,Brod D M,et al.A simplified inverter model for on-line control and simulation[J].IEEE Transactions on Industrial Application,1991,27(3):567-573.
[12] Holtz J,Lotzkat W,Khambadkone A.On continuous control of PWM inverters in the over-modulation range including the six-step-mode[J].IEEE Transactions on Power Electronics,1993,8(4):546-553.
[13] 朱建林,张建华,郭有贵,等.过调制矩阵变换器的电压传输特性及谐波分析[J].中国电机工程学报,2007,27(10):110-113.
Zhu Jianlin,Zhang Jianhua,Guo Yougui,et al.Voltage transfer characteristic and harmonic analysis of matrix converter under over modulation[J].Proceedings of the CSEE,2007,27(10):110-113.
[14] 粟梅,李丹云,孙尧,等.双级矩阵变换器的过调制策略[J].中国电机工程学报,2008,28(3):47-53.
Su Mei,Li Danyun,Sun Yao,et al.Analysis of the over-modulation strategy for two-stage matrix converter[J].Proceedings of the CSEE,2008,28(3):47-53.
[15] Amir M B,Mahammad M,Habib R M.Two simple overmodulation algorithms for space modulatated threephase to three-phase matrix converter[J].IET Power Electronics,2014,7(7):1915-1924.
[16] 张立伟,刘钧,温旭辉,等.基于基波电压幅值线性输出控制的SVPWM 过调制新算法[J].中国电机工程学报,2005,25(19):12-18.
Zhang Liwei,Liu Yun,Wen Xuhui,et al.A novel algorithm of svpwm inverter in the over-modulation region based on fundamental voltage amplitude linear output control[J].Proceedings of the CSEE,2005,25(19):12-18.
[17] Yasuhiro T,Ikuya S,Akihiro O,et al.A novel control strategy for matrix converter in the overmodulation range[J].ELectrical Engineering,2009,168(4):40-48.
[
18] 戴钱坤,葛红娟,李光泉.基于多轨迹矢量加权的矩阵变换器过调制策略[J].电工技术学报,2011,26(4):100-106.
Dai Qiankun,Ge Hongjuan,Li Guangquan.Overmodulation strategy of matrix converter based on multiorbit vector weighted[J].Transaction of China Electrotechnical Society,2011,26(4):100-106.

