附加δ势垒的一维半无限深势阱
唐义甲,韩修林
阜阳师范学院物理与电子工程学院,安徽阜阳,236037
附加δ势垒的一维半无限深势阱
唐义甲,韩修林
阜阳师范学院物理与电子工程学院,安徽阜阳,236037
通过对添加δ势垒的一维半无限深势阱的薛定谔方程进行求解,得到了粒子运动的波函数和能级的相关公式。分析发现,δ势垒的添加以及它的强度与位置的变化对能级都有影响,附加δ势后,一维粒子的能量变大,能级变得复杂,束缚态增加,基态粒子受δ势影响较大;且能级越高的粒子受δ势影响越小,最后Mathematica作图显示了这一现象。
δ势垒;一维无限深势阱;定态薛定谔方程;波函数;能级
文献[1-2]讨论了一维半无限深势阱的能级问题,文献[3-4]讨论了中央含有δ势垒的无限深势阱的束缚态能级。本文讨论在一维半无限深势阱内添加一个δ势垒的情况下,它的能级将会发生怎样的变化。具体讨论δ势垒的位置或强度发生变化时,会对能级产生怎样的影响。以下采用理论分析、数值计算与作图显示相结合的方法,对这些问题进行深入探究。
1 问题及其分析
1.1 问题
质量为m的粒子在一个内部有一个δ势垒的一维半无限深势阱中运动,设势能为(图1):
(1)
其中,μ是描述势垒位置的无量纲参数,取值区间为(0,1)。粒子的波函数与能量满足定态薛定谔方程:
(2)

图1 附加δ势垒的一维半无限深势阱
利用该方程可以计算出粒子的波函数及能级的相关表达式。
1.2 分析
考虑到势能的不连续性,粒子的波函数可以分为四段:
(3)
由于粒子束缚态粒子能量的有限性,在势能为无穷大的区间内波函数应为零,即第零段波函数ψ0(x)=0。
在势阱内部区域,定态薛定谔方程的形式为:
(4)
上式可以简化为:
ψ″+[k2-aλ2δ(x-μa)]ψ=0
(5)
其中k2=2mE/h2,λ2=2mV0/h2
(6)
在势阱外x>a区域,定态薛定谔方程的形式为:
(7)
由束缚态条件知E ψ″-κ2ψ=0 (8) (9) 1.3 综合 由在x=0处波函数的连续性得到边界条件: ψ1(0)=ψ0(0)=0 (10) 在x=μa处,由于有一个δ势垒,因此连接条件成为: ψ2(μa+0)=ψ1(μa-0)=ψ(μa) (11) 在x=a处,连接条件为[6]: (lnψ3)′(a+0)=(lnψ2)′(a-0) (12) 当x趋向无穷远时,由束缚态波函数的归一化要求,得到边界条件: ψ3(∞)=0 (13) 2.1 分段解 由方程(5)得到第一段的波函数为: ψ1(x)=Asinkx+A1coskx (14) 考虑到边界条件(10)后,上式简化为: ψ1(x)=Asinkx (15) 由方程(8)得到第三段的波函数为: ψ3(x)=Ce-κx+C1e+κx (16) 考虑到边界条件(13)后,上式简化为: ψ3(x)=Ce-κx (17) 由方程(5)还得到第二段的波函数为: ψ2(x)=Bsin(kx+φ) (18) 于是连接条件(12)成为: kcot(ka+φ)=-κ (19) 连接条件(11)成为: kcot(kμa+φ)-kcot(kμa)=aλ2 (20) 2.2 整体解 综合上面的结果,得到波函数的整体表达式: (21) 其中,系数A、B和C由连续性条件和归一化条件确定;在能量为已知的条件下,立刻可以计算出参数k,κ,而φ可由(19)或(20)式确定。 2.3 能量本征值 定态薛定谔方程是一个本征值问题,确定能量本征值在物理上有重要意义,下面来讨论如何确定能量本征值的问题。 显然(19)与(20)式为两个独立的等式,在一般情况下两者并不等价,仅仅对一些特定的能量值两者才可能一致。因此,(19)与(20)式的相容性条件就确定了能量的本征值,即能量本征值可以通过把这两个方程联立求解而得到。 下面把与能量本征值相关的所有关系式都列出来。 k2=2mE/h2,λ2=2mV0/h2 (6) (9) kcot(ka+φ)=-κ (19) kcot(kμa+φ)-kcot(kμa)=aλ2 (20) 显然,在上述关系式中λ,k1为参数;E可以由k确定,将k作为一个变量;因此,独立的变量只有3个,即k,κ,φ。这3个独立变量可以由3个独立的方程确定: cot(ka+φ)=-κ/k cot(kμa+φ)-cot(kμa)=η/k,η=aλ2 (22) 3.1 方程的化简 为了便于计算能量本征值,先对方程组(22)进行化简。在(22)式中消去κ,得到: cot(kμa+φ)-cot(kμa)=η/k (23) 由此可以进一步得到: kμa+φ=arccot[cot(kμa)+η/k] (24) 两式相减消去变量φ得到: -arccot[cot(kμa)+η/k] (25) 上式两边求余切得到: cot[(1-μ)ka] (26) 上式中只有一个未知数k。 3.2 参数的约化 容易看出上式中有4个独立的参数,即k1,a,η,μ。为了便于数值计算,还要设法减少参数。 首先,进行量纲分析,发现这些变量和参数的量纲分别为: [k]=[k1]=[η]=L-1, [a]=L, [μ]=1 (27) 将变量和参数组合为无量纲的量,即定义新的变量和参数: K=ka,K1=k1a,H=ηa (28) 则方程(26)成为: (29) 现在只有一个无量纲变量K,它的物理意义与能量有关;三个无量纲参数K1、H和μ,它们分别代表外部势垒高度、δ势垒的强度和相对位置。 4.1 不含δ势垒的一维半无限深势阱的情况 对于质量为m,势能为: (30) 在0 (31) 在x>a的区域,一般解为[2,6-8]: (32) (33) 在x=a处,位势只有有限跃变,故波函数及其导数分别连续,或波函数对数的导数连续[5,10]: (34) 将式(33)代入(34)得: kacotka=-κa (35) 式(35)无量纲化后的表达式是: (36) 这与文献[1,6]中的结果一致。 但是(35)式中的k,κ不独立,由(31)(32)两式可得: (37) 令ξ=ka,η=k′a,则式(35)(37)化为: 此方程至少有一个解的条件[4-5]: (38) 若在阱口刚好出现束缚态能级,则E≈V1,所以κ≈0。由(35)式得: kacotka=0,即coska=0,得: 由此也可验证(38)式。 4.2 添加δ势垒的一维半无限深势阱的情况 对于含有δ势垒的情况,当阱边恰好出现能级时,有E≈V1,由式(6)(9)知:κ≈0。 又由式(19)(20)知: 又在同一个周期内:kμa+φ 添加δ势垒后,能级的相关公式为: (29) 令τ=log2H,取K1=10不变[10],运用Mathematicaδ势垒位置和强度求[11]。 5.1δ势垒位置的影响 当τ为0,1,2,3,…,10,μ分别取0.1到0.9之间的数值时,K的数值解(只取基态值)如表1所示。 表1 δ势垒位置的影响下μ、τ、K的基态解之间变化关系数值分析表 利用表1数据作图如下: 当τ分别取0,1,2,…,10时,K随μ的变化图形如图3。 由图3可以看出,当τ=0时,H=1,即δ势垒很低时,μ值的变化对基态能级的影响并不大,随着τ的增大,μ值的影响也越明显。当μ处于0.55左右时,对基态能级的影响最大,两侧逐渐减小。 5.2δ势垒强度的影响 当μ分别取0.1,0.2,…,0.9之间的数值,τ为-7,-6,…,-2,-1,0,1,2,3,…,10时,K的数值解(只取基态值)如表2所示。 表2 δ势垒强度的影响下μ、τ、K的基态解之间变化关系数值分析表 利用表2数据作图如图4。 当μ分别取0.1,0.2,0.3,…,0.9时,K随τ的变化图形如图4。 图4可以看出,在一定范围内K值随着τ值的增大而增大;而当τ增大到某个值或减小到某个值时,K值达到稳定不再变化。K的最小值与μ无关,约为2.85;而K的最大值随着μ的不同而有所不同。 6.1 情形一 当τ→-∞时,H→0,此时模型变为一维半无限深势阱。 由上文讨论的不含δ势垒的一维半无限深势阱的情况可知与能级有关的表达式为: (36) 同样地,取K1=10,运用Mathematica求得基态时K≈2.8523,这与图4中τ→-∞时所得结果一致。 6.2 情形二 由一维无限深势阱的能级公式得: 表3 δ势垒的影响下一维无限深势阱的基态能级下μ、K之间变化关系数值分析表 同样地,取K1=10,运用Mathematica求得μ取不同的值时对应的基态K值如表4所示。 表4 δ势垒位置的影响下一维半无限深势阱的基态能级下μ、K之间变化关系数值分析表 综上可知,当μ取不同的值时,整个一维半无限深势阱中,当τ→∞时对应的基态K值如表5所示。 表5 δ势垒强度的影响下一维半无限深势阱的基态能级下μ、K之间变化关系数值分析表 这与图4中τ→∞时所得结果一致。 6.3 情形三 当μ=1/2,V1=∞,即K1=∞时,该模型成为中央有δ势垒的无限深势阱,将条件代入(29)式得到: (33) (34) (35) 这个结果与文献[3]所得结果完全一致。 通过上面的理论推导与数值分析,讨论了在添加δ势垒的一维半无限深势阱中运动的粒子的能级的影响因素,得到了如下结论: (1)对于给定势垒高度K1的一维半无限深势阱,δ势垒的添加会使束缚态能级的量值增加,能级个数减少。 (2)通过数值计算及作图分析,发现δ势垒的强度与位置对能级都会产生影响。当δ势垒处于势阱中心偏右位置时能级最大,在K1=10的情况下,μ≈0.55,δ势垒的强度H越大,位置的影响越明显。 (3)当δ势垒的位置一定时,δ势垒的强度H越大,能级越大。当H→∞时,势阱分裂为一维无限深势阱和一维半无限深势阱两部分,并且由这两部分求的基态能级与本文公式(29)中当H→∞时求得的结果一致。 (4)适当选取参数发现文献[1][2]和[3]中的结果都是本文结果的特例,这表明了本文结论的普遍性和正确性。 [1]曾谨言.量子力学[M].北京:科学出版社,1982:69-70 [2]史守华.量子力学考研辅导教材[M].北京:清华大学出版社,2003:4-5 [3]李明明,陈岗.无限深方势阱附加δ势后的定态解[J].山东师范大学学报:自然科学版,2004,12(4):96-97 [4]井孝功,陈硕,赵永芳.方形势与δ势解的关系[J].大学物理,2004(12):18-20 [5]钱伯初,曾谨言.量子力学习题精选与剖析[M].2版.北京:科学出版社,1999:2-4 [6]周世勋.量子力学教程[M].北京:高等教育出版社,1979:19-20 [7]朱文熙,王玉平.对称双方势阱能级无简并[J].大学物理,1999(2):32-33 [8]尹健武,冯杰,陈娇.一维高低不对称方势阱问题的数值方法[J].黄冈师范学院报,2005,12(6):26-29 [9]王柏庐.平面波通过强度不相等的两个δ势垒问题的求解[J].大学物理,1998,17(1):24-26 [10]曾谨言,钱伯初.量子力学专题分析[M].北京:高等教育出版社,1990:17-25 [11]嘉木工作室.Mathematica应用实例教程[M].北京:机械工业出版社,2002:212-323 (责任编辑:汪材印) 10.3969/j.issn.1673-2006.2015.07.026 2015-01-30 国家自然科学基金项目“耀变体多波段光变特征研究”(11273008) ;阜阳师范学院教学研究项目“大学物理课程三维教学手段的改革与实践”(2012JYXM61);阜阳师范学院基础教育研究项目“中学物理课堂演示实验的研究与实践”(2012JCJY21)。 唐义甲(1984-) ,安徽枞阳人,硕士,助理实验师,主要研究方向:非线性光学材料高能粒子束辐照改性及防护。 O469 A 1673-2006(2015)07-0093-06

2 定态薛定谔方程的解

3 能量本征值的计算



4 两种情况的比较


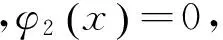




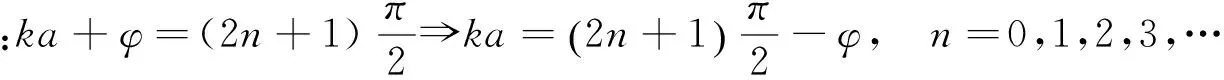

5 运用Mathematica作图显示δ势垒的影响





6 特殊情形




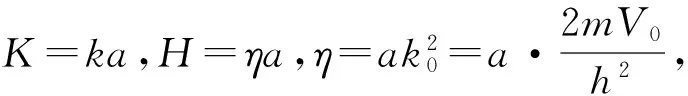
7 结束语

