变系数kdv方程的Grammian解及Wronskian解

黄丽丽,张金顺

(华侨大学数学科学学院,福建泉州362021)

引入Pfaff元:

变系数kdv方程的Grammian解及Wronskian解

黄丽丽,张金顺*

(华侨大学数学科学学院,福建泉州362021)

主要研究一类变系数kdv方程,通过其双线性形式及Hirota方法,结合其Wronskian行列式解,得到一个Grammian行列式解。引入Pfaff式,证明此Grammian行列式解满足变系数kdv方程的双线性方程,并证明其Grammian行列式解及Wronskian行列式解的双线性孤子方程满足Praff恒等式,且均可用Maya图表示,从而更清晰地表达出变系数kdv方程解的性质,并将孤子方程化为一种简单的图表。Grammian行列式等价于Jacobi恒等式;Wronskian行列式等价于Plücker关系,而Jacobi恒等式及Plücker关系则是Pfaff恒等式的特殊情形。

变系数kdv方程;Grammian行列式解;Wronskian行列式解;Hirota方法

孤子理论在非线性科学发展领域中占据着很大的作用,在最近这些年里,孤子方程可积系统得到了高度重视.许多变系数可积方程在物理现象中大量地出现,而变系数发展方程反映了一些物理情形中的真实模型.本文主要研究变系数kdv方程:

其中h1=h1(t),h2=h2(t),h3=h3(t)都是关于t的任意函数.至今为止,大家对此方程进行了很多方面的研究:文献[1]通过双线性形式及Hirota方法给出了其Wronskian形式的精确解;文献[2]中通过反散射方法解决了方程(1)的初值问题;文献[3]研究了其无穷守恒律;文献[4]讨论了它的对称性;文献[5]通过齐次平衡法得到了其Bäcklund变换.

Hirota方法[6],Bäcklund变换[7],Wronskian技巧[8]是寻找非线性方程孤子解的3种有效的直接方法.Mikio Sato曾提出一种新的观点[9-10]:双线性方程可以视为等价于Grassmann流行上的Plücker关系式.本文将给出方程(1)的Grammian行列式解及Wronskian行列式解,并利用Mikio Sato设计的Maya图表,结合Pfaff恒等式,把孤子方程化为一种简单的图表.

1 Grammian行列式解

通过变换

方程(1)可写成双线性导数方程:

其中D是我们所熟知的Hirota双线性算子:

文献[1]给出了方程(1)的Wronskian行列式解:

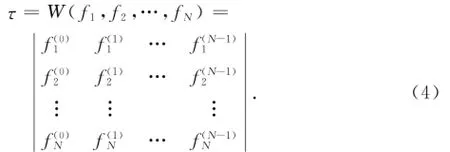
函数fj=fj(x,t)(j=1,2,…,n)对一切¯∞＜x＜∞,t≥0具有任意阶的连续导数,且满足关系式:

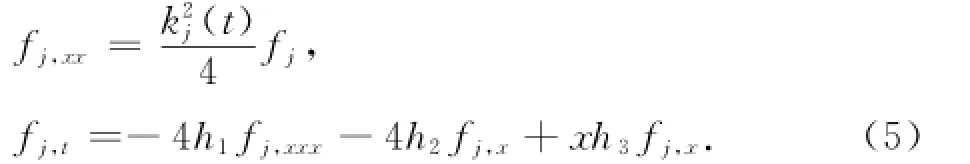
定义1 如果方程(1)的N-孤子解具有形式:

其中pi=pi(x,t),gj=gj(x,t),cij=常数,则

τN=det(aij)

称为方程(1)的Grammian行列式解.

定义2 一个Pfaff式的平方就是一个偶数阶反对称行列式A=det(ajk),由此定义的Pfaff式记为(1, 2,…,2n).

例如,当n=1时,

Pfaff恒等式存在着很多种不同的形式,这里给出本文将利用的其中一个,它有如下的形式:

定理1 设pi(x),gi(x)满足条件:

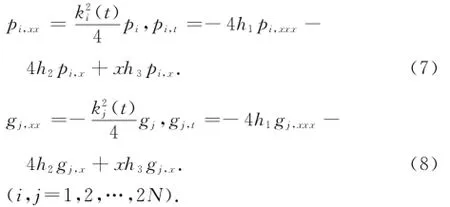
则由式(6)定义的Grammian行列式τN满足双线性方程(3).

证明 将τN写成Pfaff形式,则

引入Pfaff元:

于是aij=(i,j*)的导数可以写成:

记τ=τN,τ=(1,2,…,N,N*,…,2*,1*)=(·).于是可以得到:

将上面的Pfaff式代入方程(3),可以得到:

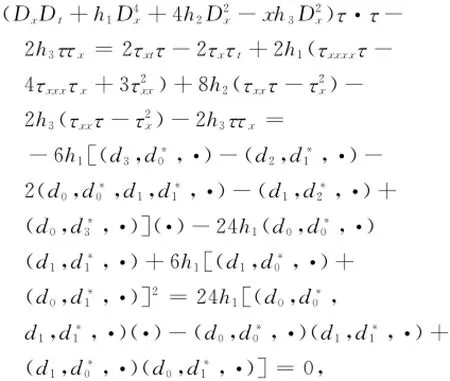
其中利用了恒等式

由行列式性质得到

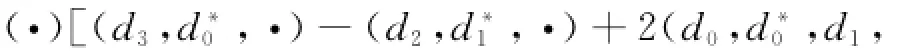
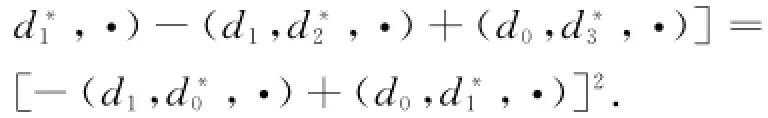
于是我们用Maya图可表示为:

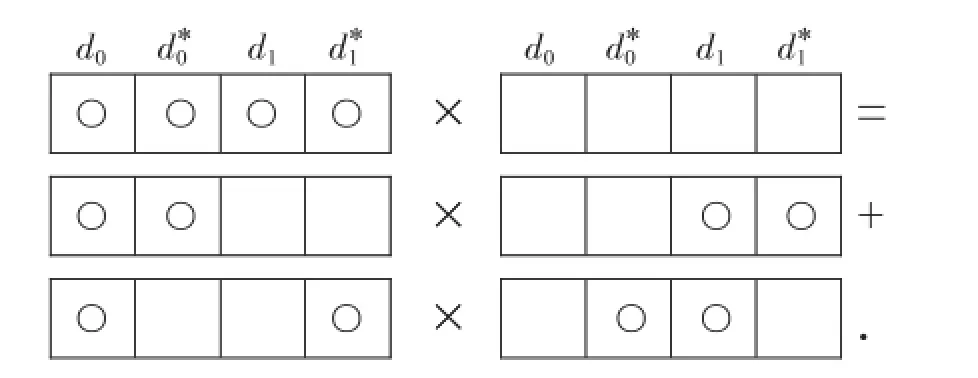
即由式(6)给出的函数τN是双线性方程(3)的一个Grammian行列式解.

注:Maya图中○和空格分别表示填充的和空的方格,上图省略了所有共同的部分.

2 Wronskian行列式解的Maya图表示

利用文献[11],记τ=(0,1,2,…,2N¯1),则

将上面的导数代入双线性方程(3)的左边通过一些复杂的计算可以得到:

3 结 论

孤子理论现已渗透到流体力学等离子体物理,海洋科学,光纤通信,生物科学等各个领域.孤子理论的研究也呈现多样化,在计算求导公式时,应用Pfaff式计算比应用行列式计算更简单,通过上述讨论我们得到双线性孤子方程满足Pfaff恒等式:如果τ表示为Grammian行列式,它等价于Jacobi恒等式;如果τ表示为Wronskian行列式,它等价于Plücker关系.

显然Plücker关系和Jacobi恒等式都是下面Pfaff恒等式的的特殊情形:

[1] Deng S F.Exact solutions for a nonisospectral and variable-coefficient kdv equation[J].Commun Theor Phys, 2005,43:961-964.

[2] Chan W L,Li K S.Nonpropagating solitons of the variable-coefficient and nonisospectral kdv equation[J].Math Phys,1989,30:2521-2526.

[3] Lou S Y,Ruan H Y.Conservation laws of the variable-coefficient kdv and mkdv equations[J].Acta Phys Sin, 1992,41:182-187.

[4] Zhang J F,Han P.Symmetries of the variable-coefficient and three hierarchies of the integrodifferential variablecoefficient kdv equation[J].Chin Phys Lett,1994,11:721-723.

[5] 陈登远.孤子引论[M].北京:科学技术出版社,2006.

[6] Hirota R.Exact solution of the korteweg-de vries equation for multiple collisions of solitons[J].Phys Rev Lett, 1971,27:1192-1194.

[7] Hirota R.A new form of Bäcklund transformations and its relation to the inverse scattering problem[J].Prog Theor Phys,1974,52:1498-1512.

[8] Freeman N C,Nimmo J J C.Soliton solutions of the korteweg-de vries and kadomtsev-petviashvili equations: the wronskian technique[J].Phys Lett,1983,95:1-3.

[9] Sato M.Soliton equations as dynamical systems on an infinite dimensional Grassmannian manifold[J].Surikaiseki Kenkyusho Kokyuroku(RIMS,Kyoto University),1981, 439:30-46.

[10] Ohta Y,Satsuma J,Takahashi D,et al.Anelementry intro-duction to Sato theory[M].Progr Theor Phys Suppl,1988,94:210-240.

[11] Hirota R.The direct methods in soliton theory[M]. Cambridge:Cambridge University Press,2004.

Grammian Solution and Wronskian Solution for the Variable-coefficient Kdv Equation

HUANG Li-li,ZHANG Jin-shun*
(School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China)

:This paper mainly studies a variable-coefficient kdv equation,through its bilinear form and Hirota method,combined with its Wronskian determinant solution,we obtain a Grammian determinant solution.With the introduction of Pfaff form,we prove the Grammian determinant solution satisfies Bilinear equation of the variable-coefficient kdv equation,and prove its Grammian determinant solution and Wronskian determinant solution′bilinear soliton equation satisfy Pfaff identities.We also prove the two solutions can be figured out by Maya diagram.So the qualities of the variable-coefficient kdv equation′solutions can be clearly showed out,and the soliton equation is made into a simple diagram.Grammian determinant is equivalent to Jacobi identity,and Wronskian determinant is equivalent to Plücker relation.Jacobi identity and Plücker relation are special circumstances of the Pfaff identities.

Variable-coefficient kdv equation;Grammian determinant solution;Wronskian determinant solution;Hirota method

O 175.29

A

0438-0479(2015)03-0354-04

10.6043/j.issn.0438-0479.2015.03.011

2014-02-10 录用日期:2014-10-13

*通信作者:jszhang@hqu.edu.cn

黄丽丽,张金顺.变系数kdv方程的Grammian解及Wronskian解[J].厦门大学学报:自然科学版,2015,54(3):

354-357.

:Huang Lili,Zhang Jinshun.Grammian solution and wronskian solution for the variable-coefficient kdv equation[J].

Journal of Xiamen University:Natural Science,2015,54(3):354-357.(in Chinese)