具有非局部时滞合作扩散模型行波解的存在性

王海玲,肖筱南

(厦门大学嘉庚学院,福建漳州363105)

具有非局部时滞合作扩散模型行波解的存在性

王海玲*,肖筱南

(厦门大学嘉庚学院,福建漳州363105)

在前人的基础上,通过改变模型结构,运用上、下解方法,研究了一类具有非局部时滞合作扩散模型的行波解的存在性,改进了前人的研究范围,同时把这种方法推广到一般的Lotka-Volterra方程和更广泛的范围.

非局部时滞;行波解;上、下解

近年来,基于各种现实背景,人们对反应扩散方程组的行波解给予极大的关注,并且取得了不少的成果.特别是对具有离散时滞的反应扩散方程的研究很多[1-5].另外,由于生物个体所在的空间位置通常会随时间变化而改变,因此将它与时间滞后相结合,则产生了具有非局部的反应扩散方程组.因此,具有连续时滞的反应扩散方程引起了人们的较大兴趣[6-9].采用文献[9]的方法,通过加入两个物种的内在增长种类,考虑如下具有非局部时滞的合作扩散模型的行波解的存在性:

其中,t＞0,x∈Ω⊂Rm,ai,bi,ci,di(i=1,2),r1,r2是正常数,r1,r2表示内在的增长种类,u1,u2表示在t时刻x位置时的两个合作者人口的密度,d1,d2为扩散系数,gj(t,x)为非负可积函数,且满足

关于式(1)的其他各种形式已被许多作者进行研究.如时滞改为离散型,则式(1)变为

文献[5]研究了行波解的存在性.如果b1=b2=0,则式(2)变为

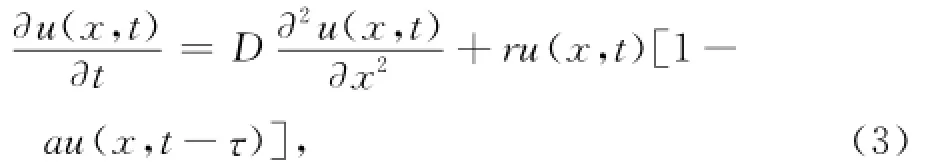
文献[10]也研究了行波解的存在性.文献[4]采用同样的方法,通过构造不同的上下解研究了具有离散时滞的竞争模型行波解的存在性,模型如下:

模型(2)～(4)都只表示物种在局部范围内扩散,但是在生态学和流行病学等领域,局部反应扩散方程并不能准确描述研究对象的时空行为,所以基于以上几个模型的研究思路,本文以核函数为例,采用同样方法,通过引入卷积算子来描述空间扩散过程以及构造不同于上述模型的上下解对(1)的行波解的存在性进行研究,使得我们的上下解满足拟单调条件.

1 预备内容

考虑下面具有非局部时滞的反应扩散方程组:

其中,

其中gj是非负可积函数,且满足

1,令u(x,t)=φ(x+ct),用t代替x+ct,则式(5)可变为:

为研究方程组(6)行波解的存在性,假设如下:
(H1)存在β=diag(β1,…,βn),βi＞0,i=1,…n,使得

其中,φ,ψ∈C(R,Rn)满足:(i)0≤ψ(t)≤φ(t)≤k,t∈R;(ii)eβt[φ(t)¯ψ(t)]是t∈R上的单调增加函数, e¯βt[φ(t)¯ψ(t)]是t∈R上的单调减少函数;

(H2)当0＜μ＜k时,f(μ,…,μ)≠0;

(H3)当μ=0,k时,f(μ,…,μ)≠0.

方程组(6)的上、下解定义如下:

定理1 假设(H1,H2,H3)成立,且是一对上下解,满足n}¯1时,式(5)有满足式(7)的行波解φ*,满足¯φ≥

2 主要结果的证明

令ui(x,t)=φi(s),s=x+ct,用t代替s,则系统(1)化为:

文中,记

令式(9)的边界条件为:

为计算方便,令

引理1 当τ1,τ4充分小,βi≥2aiki+5biki¯ri(if1,f2满足(H)条件.

证明 令φ=(φ1,φ2),ψ=(ψ1,ψ2)∈C([¯cτ,0], R2)且满足(i)0≤ψ(s)≤φ(s),s∈[¯cτ,0].(ii)eβs[φ(s) ¯ψ(s)]在[¯cτ,0]上单调不减.则

即

同理可证,

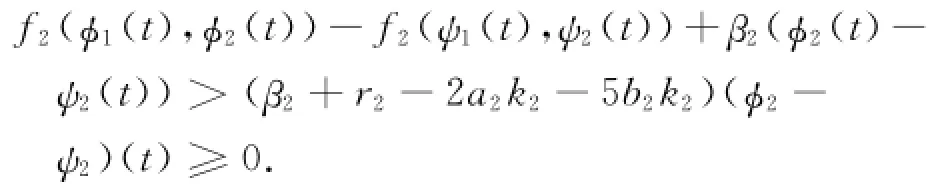
即f1,f2满足(H)条件.

引理2 eβt[φ(t)¯ψ(t)]在t∈R上是单调不减的.

证明 当t＞0时,ψ1(t)=ε,φ1(t)=k1,则

当t≤0时,ψ1(t)=εeλ2t,φ1(t)=k1eλ1t,则

引理3 e¯βt[φ(t)¯ψ(t)]在t∈R上是单调不增的.

证明 当t＞0时,ψ1(t)=ε,φ1(t)=k1,则

当t≤0时,ψ1

综上,φ(t)=(φ1(t),φ2(t))是系统(9)的上解.

由引理1～5,有如下结果.

注1 文中的τi,i=2,3对方程组(1)的行波解没有影响;

注2 取以下不同的核时,定理2的结论仍然成立:

[1] Zou X F,Wu J H.Existence of traveling wave-fronts in delayed reaction-diffusion system via monotone iteration method[J].Amer Math Society,1997,125(9): 2589-2598.

[2] Joseph W H S,Wu J H,Zou X F.A reaction diffusion model for a single species with age structure.ⅠTraveling wave fronts on unbounded domains[J].Proc R Soc Lond A,2001,457(2012):1841-1854.

[3] Ma S.Traveling wave-fronts for delayed reaction-diffusion systems via a fixed point theorem[J].J Differential Equations,2001,171(2):294-314.

[4] Lv G Y,Wang M X.Traveling wave front in diffusive and competitive Lotka-Volterra system with delays[J]. Nonlinear Analysis Real World Applications,2009,11 (3):1323-1329.

[5] Huang J H,Zou X F.Traveling wave fronts in diffusive and cooperative Lotka-Volterra system with delays[J].J Math Anal Appl,2002,271:455-466.

[6] Stephen A G,Ruan S G.Convergence and traveling fronts in functional differential equations with non-local terms:a competition model[J].SIAM J Math Anal,2003, 35(3):806-822.

[7] Wang Z C,Li W T.Monotone traveling fronts of a foodlimited population model with non-local delay[J].Nonlinear Analysis Real World Applications,2007,8(2): 699-712.

[8] Wang Z C,Li W T,Ruan S.Traveling wave fronts of reaction-diffusion systems with spatio-temporal delays[J]. J Differential Equations,2006,222(1):185-232.

[9] Li W T,Wang Z C.Traveling fronts in diffusive and cooperative Lotka-Volterra system with nonlocal delays [J].J Math Phys,2007,58(4):571-591.

[10] Wu J,Zou X.Traveling wave fronts of reaction diffusion systems with delay[J].J Dynam Diff Eq,2001,13(3): 651-687.

The Existence of Traveling Wave Fronts Solution in Diffusive and Cooperative Equations with Nonlocal Delays

WANG Hai-ling*,XIAO Xiao-nan
(Tan Kah Kee Colledge,Xiamen University,Zhangzhou 363105,China)

:On the basis of pioneers′work and modified models,the existence of traveling wave-fronts solutions in diffusive and cooperative Lotka-Volterra systems with nonlocal delays is established,depending on the construction of a pair of upper-lower solutions. This method facilitates to improve previous results and is applied to general Lotka-Volterra equation or even to broader systems.

nonlocal delays;traveling fronts solutions;upper-lower solutions

O 175.26

A

0438-0479(2015)03-0364-05

10.6043/j.issn.0438-0479.2015.03.013

2014-03-05 录用日期:2014-11-20

国家自然科学基金(10871163)

*通信作者:whling@xujc.com

王海玲,肖筱南.具有非局部时滞合作扩散模型行波解的存在性[J].厦门大学学报:自然科学版,2015,54(3): 364-368.

:Wang Hailing,Xiao Xiaonan.The Existence of Traveling Wave Fronts Solution in Diffusive and Cooperative Equations with Nonlocal Delays[J].Journal of Xiamen University:Natural Science,2015,54(3):364-368.(in Chinese)