五种版本教材“等差数列”的编写内容比较研究和教学建议

☉陕西省麟游县中学 韩红军

五种版本教材“等差数列”的编写内容比较研究和教学建议

☉陕西省麟游县中学 韩红军

等差数列是在学生前面学习了数列的一般性概念、数列的通项公式、递推公式的基础上，第一次对一个特殊数列展开研究的开始，它是继续研究等差数列的基础，它为等比数列概念的学习、通项公式的推导与应用等，乃至研究其他更一般的数列，给出了“示范”、提供了“模式”、指明了方向.本节课先是从具体的例子出发，引导学生观察，进而得到等差数列的概念，接着由等差数列的概念出发，运用观察、分析、归纳的方法推导等差数列的通项公式，培养学生用数学不完全归纳法得到数学结论的思维能力.

一、五种版本教材“等差数列”的编写内容比较

1.等差数列概念的引入实例与问题背景比较

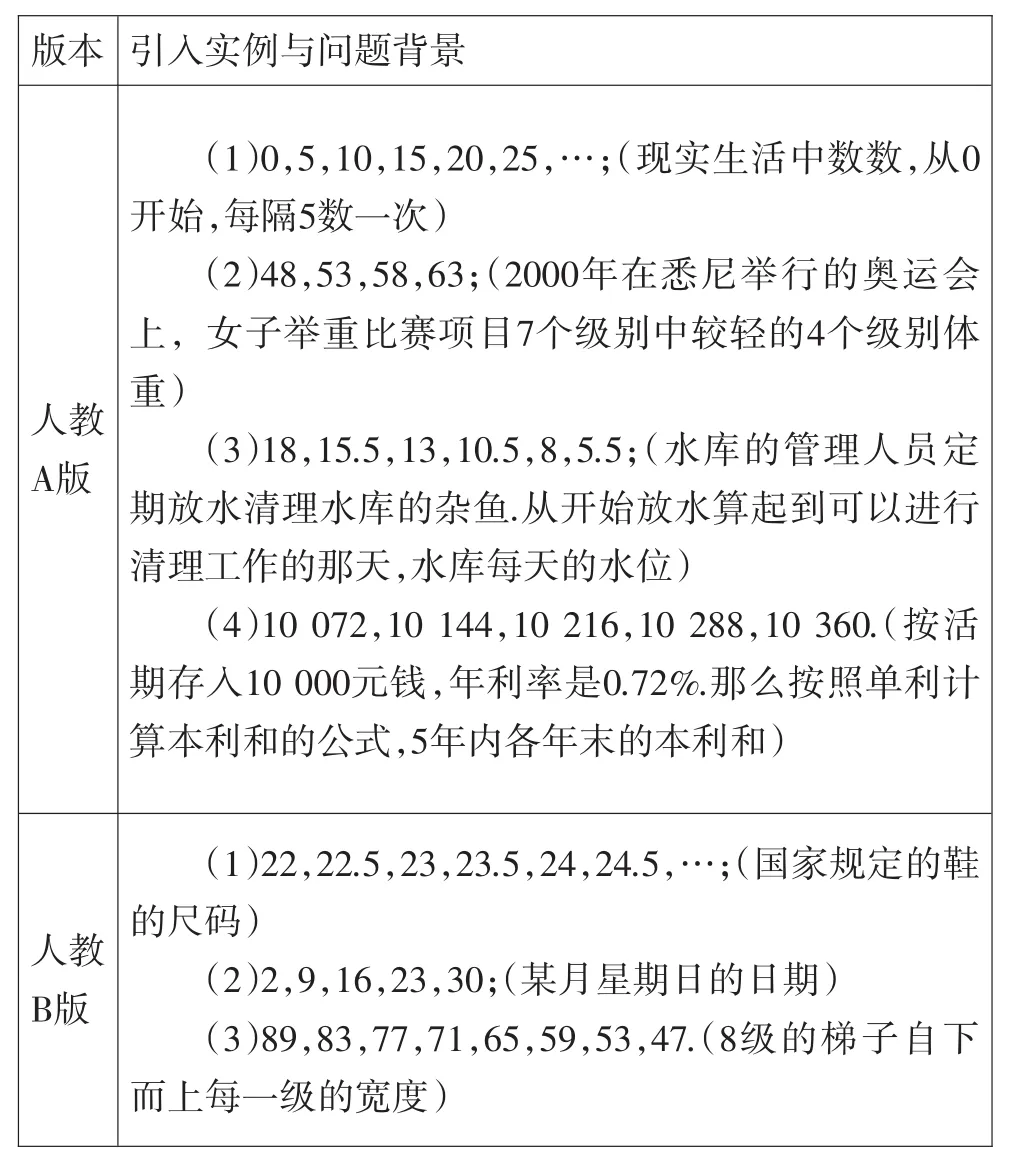
表1：等差数列概念的引入实例与问题背景比较

?

从以上表格可以看出，等差数列的概念都是通过实例引入的，但不同版本教材还有不同之处，具体如下：（1）北师大版与湘教版教材提出了公差为0的等差数列；（2）北师大版、人教A版与人教B版教材在定义前或定义后明确给出了引入实例中的公差；（3）苏教版、人教A版与湘教版教材给出了等差数列和公差的英文形式，其中人教A版教材还给出了等差数列的英文缩写形式；（4）等差中项的概念出现在北师大版、人教A版与人教B版教材的正文中，湘教版教材出现在例题中，苏教版教材出现在习题中；（5）苏教版教材给出的都是递增的等差数列，只有苏教版教材给出了数字型式子形式的等差数列，只有湘教版教材给出了字母型式子形式的等差数列，也最容易概括出等差数列的定义.

2.等差数列通项公式的推导方法与性质的呈现方式

表2：等差数列通项公式的推导方法与性质的呈现方式

从以上表格可以看出，等差数列的通项公式的推导方法主要涉及两种：不完全归纳法、累（叠）加法，只有人教B版教材两种都使用了，其他版本教材都只使用了其中一种方法.等差数列的常用性质不同版本教材大部分在习题或练习题都涉及了，但具体内容差异较大，具体如下：（1）湘教版、人教B版教材不但给出了an=a1+（n-1）d，还给出了an=dn+a1-d，而且比较了与一次函数的异同，苏教版教材只是作为思考题提出来，其他版本教材都没有编写；（2）只有湘教版、苏教版教材涉及了性质：若m+n= p+q，则am+an=ap+aq，其他版本教材则没有涉及；（3）只有人教B版、北师大版教材涉及了等差数列的单调性，其他版本教材则没有涉及；（4）只有人教A版、人教B版教材涉及了性质其他版本教材则没有涉及.

3.五种版本教材中例题、练习题、习题、思考题等的比较

表3：各版本教材中例题、练习题、习题、思考题等的比较

注：（1）表中的数据以教材中有题号的题目为准，在一个题目下有多个小题号的按一个题计算；（2）各类习题总数中括号中数字的含义是以生活实例、数学史、数学名题背景或与其他知识综合的等差数列题目数；（3）题目总数中括号中数字的含义是指选择题和填空题的数目.

从以上表格可以看出，五种版本教材等差数列中例题、练习题、习题的数目、类型和呈现形式差异较大，具体如下：（1）对于题目总数来说，苏教版教材最多（31道），北师大版教材选择题和填空题最多（5道），人教A版教材最少（15道）；（2）对于例题数目来说，湘教版教材最多（7道），苏教版教材以生活实例、数学史、数学名题为背景或与其他知识综合的等差数列题目数最多（3道），人教A版教材最少（3道）；（3）对于练习题数目来说，苏教版教材最多（13道），苏教版教材以生活实例、数学史、数学名题为背景或与其他知识综合的等差数列题目数最多（5道），人教A版教材最少（5道）；（4）对于习题数目来说，苏教版教材最多（12道），人教A版教材以生活实例、数学史、数学名题为背景或与其他知识综合的等差数列题目数最多（4道），人教A版教材最少（7道）；（2）对于思考题和探究题来说，北师大版教材最多（4道），只有人教A版教材有1道探究题.

二、等差数列教学建议

1.教学目标、教学重点和难点的确定

根据教学大纲、《普通高中数学课程标准（实验）》和学生的实际情况，教学目标分为三个层次，即教给学生知识，又教给学生技能，还教给学生方法，同时注重学生素质和能力的提高，在潜移默化中塑造学生完美的人格，使学生形成健康的心理.

（1）教学目标.

基于等差数列编写内容的比较分析，我们认为等差数列的教学目标可以分为三个层次.

第一个层次：等差数列教学的知识性目标，就是抽象出等差数列的概念，推导出等差数列的通项.

第二个层次：等差数列教学的过程性目标，就是要让学生亲身经历抽象概括的过程，归纳推理的过程，演绎推理的过程，让学生在学习过程中体验探究的乐趣，体验成功的喜悦，积累数学活动经验.

第三个层次：等差数列教学的能力性目标，就是要让学生在经历抽象概括、归纳推理、演绎推理的过程中，形成抽象概括能力、归纳推理能力和演绎推理能力，这些能力将在更广阔的知识学习中发挥积极作用.

（2）教学重点.

等差数列的概念与等差数列的通项公式.

（3）教学难点

等差数列通项公式的推导及从函数的角度理解通项公式.

2.等差数列概念的教学建议

《普通高中数学课程标准（实验）》指出：高中数学课程应该返璞归真，努力揭示数学概念、法则、结论的发展过程和本质.数学课程要讲逻辑推理，更要讲道理，通过典型例子的分析和学生自主探索活动，使学生理解数学概念、结论逐步形成的过程，体会蕴含在其中的思想方法，追寻数学发展的历史足迹，把数学的学术形态转化为学生易于接受的教育形态.根据等差数列概念的引入实例与问题背景比较可以看出：等差数列的定义及公差的概念是通过归纳实例的共同特点得出的.但各版本教材“等差数列”的编写内容都在等差数列的概念的内涵、外延、属性（性质和特征）等方面存在纰漏，引入实例不完整，或缺失公差为0的例子，或缺失公差为负数的例子，或缺失字母型式子形式的例子.因此，在设计引例时，要考虑到：①公差可以是正数、负数，也可以是0；②等差数列{an}满足：an+1-an=d（d是常数，n∈N且n≥1），这里所说的常数实际上指an+1-an是一个与n无关的数；③在学习了等差数列的定义后，必须明确给出等差中项的定义；④从学生长远的发展角度看，等差数列和公差的英文形式和等差数列的英文缩写形式都应该给出.等差数列的定义也是证明一个数列是否为等差数列的一种方法.例如等差数列的定义可以从以下例题引入.

例：判别以下数列是否为等差数列，若不是请说明理由.

（1）-1，3，6，9，12，15，18；

（2）2，4，6，8，11，14，17，20，…；

（3）2，3，2，3，2，3，…；

（4）10，7，4，1，-2，-5，…；

（5）100，100，100，100，…；

（6）20，15，10，5，0，-5，…；

（7）m+n，m+2n，m+3n，m+4n，m+5n，….

设计思路：数列（1）从第三项其每一项与前一项的差都是常数3，但第二项与第一项的差却是4，不符合定义中的“从第二项起”；数列（2）的前四项和后四项中，每一项与前一项的差都是常数，但不是同一个常数，由此可使学生体现或感受到“每一项与前一项的差是常数”这一本质特征的真正含义；数列（3）从第二项起，每一项与前一项的和是常数，而相应的差不是常数.只有数列（4）、（5）、（6）、（7）满足等差数列的定义.通过这样正反几个例子的辨析，使学生感受与理解了定义中“从第二项起”“每一项与前一项的差”“都是同一个常数”等关键词的真正含义，深化了对“等差”这一本质特征的认识；明白了为什么叫“等差数列”而不叫“等和数列”“等积数列”的道理.同时还可以引发学生去进一步联想和思考有没有“等和数列”“等积数列”等问题.

3.等差数列通项公式的教学建议

等差数列的通项公式的推导有多种方法，主要涉及两种：不完全归纳法、累（叠）加法.其中利用不完全归纳法可以得到通项公式的猜想，从普通的事例联想到有关知识，从简单的情况入手，通过猜测归纳，发现并证明具有一般规律的结论.这种联想、猜测、归纳、证明的途径，如果能在学习的过程中经常使用，将会有助于学生开拓思路，帮助学生发现规律，提高解决问题的能力和开拓创新的精神.然而猜想的结论有可能正确，也有可能错误，所以必须进行证明，只有证明猜想的结论成立才能使用，所以最好再用累（叠）加法进行证明，而且介绍累（叠）加法也可以为后续等差数列前n项求和方法的学习作铺垫.

等差数列通项公式可以变形为：an=a1+（n-1）d=dn+（a1-d）；也可以推广为：am=an+（m-n）d或（m≠ n），所以在教学时要把等差数列的通项公式an看成关于n的一次函数，体现数列的函数特性，进一步让学生理解数列是一种特殊的函数，让学生明确以项数n为点的横坐标、项an为点的纵坐标的点（n，an），在一条以公差d为斜率的直线上，所以对该直线上任意两点（n，an）、（m，am）有

等差数列的通项公式与4个量有关，即首项a1、公差d、项数n、第n项an，而且首项a1、公差d是等差数列的两个关键量，所以方程思想孕育而生.

4.等差数列作业设计的教学建议

根据各版本教材中例题、练习题、习题、思考题等的比较，从作业考查知识点的角度说，所有的例题、练习题、习题、思考题等题目都是围绕等差数列的定义和通项公式的应用来设计的：判断一个数列是否是等差数列，说明首项a1、公差d、项数n是多少；证明一个数列是否是等差数列；方程思想在等差数列通项公式中的应用；等差中项概念的应用；等差数列与线性函数（直线）的关系的应用；解决等差数列应用题时的设元方法和技巧；累加法的应用；探究和应用等差数列的性质：（1）am=an+（m-n）d或，（2）若m+n=p+q，则am+an=ap+aq；（3）单调性：若公差d>0，则为递增数列，若d<0，则为递减数列，若d=0，则为常数列，（4）若{an}、{bn}是等差数列，则{kan}、{kan+pbn}（k、p是非零常数）也是等差数列，（5）构造新数列，即如果两等差数列有公共项，那么由它们的公共项顺次组成的新数列也是等差数列，且新等差数列的公差是原两等差数列公差的最小公倍数.从作业量上说，根据前苏联玛什比茨的研究结果“在对一个典型问题的运算形成解法之前，无论在什么学科中，不同的学生需要1～22次联系不等.”意思是说掌握一类问题的解决方法需要做1～22道同类练习题，题量过少，学生不易达到掌握的目的，题量过多，就会增加学生的学习负担.

《普通高中数学课程标准（实验）》指出：学生的数学学习活动不应只限于接受、记忆、模仿和练习，高中数学课程还应倡导自主探索、动手实践、合作交流、阅读自学等学习数学的方式.这些方式有助于发挥学生学习的主动性，使学生的学习过程成为在教师引导下的“再创造”过程.同时，高中数学课程设立“数学探究”“数学建模”等学习活动，为学生形成积极主动的、多样的学习方式进一步创造有利的条件，以激发学生的数学学习兴趣，鼓励学生在学习过程中，养成独立思考、积极探索的习惯.高中数学课程应力求通过各种不同形式的自主学习、探究活动，让学生体验数学发现和创造的历程，发展他们的创新意识.所以在设计等差数列的定义和通项公式应用的例题、习题、练习题、思考题和探究题时，要增加以生活实例、数学史、数学名题为背景或与其他知识综合的题目，题型可以设计选择题、判断题、连线题、填表题和解答题，方式可以是探究题、趣味题、开放题，尤其要增加中国古代对等差数列的研究成果或将中国古籍中有关等差数列的题目进行改编，目的是激发学生的学习兴趣，增强对学生的爱国主义教育，培养学生探究新知的好奇心和对待科学锲而不舍的精神，潜移默化地培养学生的创新能力.

1.李建华，主编.普通高中课程标准实验教科书数学必修5［M］.北京：人民教育出版社，2004.

2.万庆炎，主编.普通高中课程标准实验教科书数学必修5［M］.北京：人民教育出版社，2007.

3.严士健，王尚志，主编.普通高中课程标准实验教科书数学必修5［M］.北京：北京师范大学出版社，2010.

4.徐稼红，主编.普通高中课程标准实验教科书数学必修5［M］.南京：江苏教育出版社，2005.

5.查建国，主编.普通高中课程标准实验教科书数学必修4［M］.长沙：湖南教育出版社，2010.

6.中华人民共和国教育部.普通高中数学课程标准（实验）［M］.北京：人民教育出版社，2003.

7.李海良.等差数列教学的起点和目标［J］.中学数学教学参考（上），2013（11）.

8.严士健，王尚志，主编.普通高中课程标准实验教科书教师教学用书数学必修5［M］.北京：北京师范大学出版社，2011.

9.刘电芝.教材的宏观评价和微观评价［J］.课程·教材·教法，1996（4）.