数形结合思想方法在高中数学教学中的应用分析

刘桂玲

摘要：随着新课程改革的逐渐深化，新课程标准的不断实施，以生为本理念得到了推广应用。为此，在高中数学教学中，越来越重视学生学习的主体地位，要求学生对数学概念、思想等进行准确把握，而数与形式高中数学教学的重要内容，加强数形结合是培养学生数学思想的重要途径。在分析数形结合思想方法概念及原则的基础上，阐述高中数学教学中数形结合思想方法的应用。

关键词：数形结合 高中数学教学 应用

数学是一门具有较强逻辑性的学科，也是研究数量关系及空间图像的学科，对于高中生而言，数学知识非常枯燥，在学习的时候，难度比较大。为此，在高中数学教学中，教师一定要根据数学知识，采取有效的教学方法，加强学生对数学知识的理解与学习，进而取得良好的教学效果。

一、数形结合思想方法概述

（一）概念

在高中数学中，数、形是两个非常重要的元素，数指的就是数量关系，形指的就是空间图像。高中数学中的一些数量关系可以转变成图形，进行求解，当然一些图形问题也可以转变为数量关系，进行求解，实际上，就是利用数、形互换方式进行求解。数形结合求解就是将数学中的图像转变为数学语言，通过抽象与形象思维的结合，利用形象图像解决抽象问题，实现化难为易的效果，提高学生的解题能力。

（二）原则

1.双向性原则

双向性原则指的就是对几何图形进行直观分析的同时，还要对其代数抽象性进行分析。代数语言的逻辑性、精确性非常强，可以避免几何直观的约束性，充分突出了数形结合的优势。

2.等价性原则

等价性原则指的就是“数”的代数性质和“形”的几何性质在进行转化的时候，应该是等价的。因为图形局限性，导致在画图的时候，容易出现准确性不好的问题，影响了解题效果。为此，在数形结合应用过程中，一定要重视等价性原则。

二、高中数学教学中数形结合思想方法的应用

（一）数转形

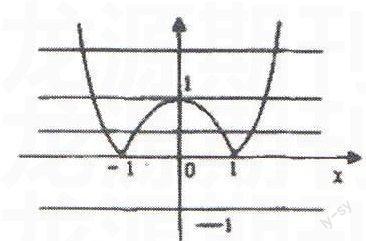
图形的形象性、直观性非常强，相对于数学语言来说，具有很强的优势。所以，在高中数学教学中，可以将一些抽象的、难以求解的代数问题，利用数形结合思想方法转变为图形问题，这样就可以启发学生的思维，明确解题思路，进而实现有效解题，提高学生的解题能力。比如，设方程|x2-1|=k+1，讨论k取值不同时，方程解的个数。解题分析：在实际解题的时候，可以将方程转变为两个函数：y1=|x2-1|、y2=k+1，之后画出相应的图示，对方程进行求解。因为函数y2=k+1表示的和x轴平行的直线，为此，其图像如下所示。

解析：当k<-1的时候，两个函数没有交点，也就表示原方程没有解；当k=-1的时候，两个函数有两个交点，也就表示原方程有两个解；当k在（-1，0）之间的时候，两个函数有四个交点，也就表示原方程有四个解；当k=0的时候，两个函数有三个交点，也就表示原方程有三个解；当k>0的时候，两个函数有两个交点，也就表示原方程有两个解。

通过此道例题可以看出，在探讨方程求解或者函数零点个数问题的时候，可以利用数形结合思想方法进行解题，可以有效激发学生的解题思路，有助于学生的快速解题。同时，通过直观图形的展示，可以培养学生的观察能力，对拓展学生的思维也有着一定的作用。

（二）形转数

虽然图形具有很强的形象、直观优势，但是也存在着一些局限性，缺少计算的精准性与推理的逻辑性，特别是在解决一些数学问题的时候，弊端非常明显，无法单独依靠图形予以解题，并且还容易发生一些错误。所以，在面对此种情况的时候，可以通过数形结合思想方法，将图形转变为代数语言，扩展解题思路，对问题进行有效解决。比如，设f（x）=x2-2ax+2，当x在[-1，+∞）间取值的时候，f（x）>a恒成立，对a的取值范围进行求取。

解析：当x在[-1，+∞）间取值的时候，f（x）>a恒成立，得知x2-2ax+2-a>0在此范围是恒成立的。所以，g（x）=x2-2ax+2-a在此范围中处在x轴上方。如下图形式。保证不等式成立的条件包括两点：一是，△=4a2-4（2-a）<0，求得a的取值范围在（-2，1）之间；二是，△≥0，g（-1）>0，a<-1，求得a的取值范围在（-3，1）之间。

通过此例题可以看出，一些求取具体值的数学问题，无法利用图形进行准确求值，此时可以将图形问题转换为代数问题，这样就可以快速求解。在此过程中，学生一定要进行充分考虑，不要漏掉任何已知条件，考虑各种可能，这样才可以保证求解完全，正确解题。

（三）数、形的结合应用

在高中数学教学过程中，数、形解题都存在着一定的缺陷，却又是相辅相成的。在很多数学问题中，需要充分利用数、形的优势，通过两者的共同运用，解决问题。比如，在解决一些静态函数问题的时候，可以通过坐标系-图像的动态表达，对问题进行阐述，进而予以有效解决。图像能够形象、直观的表达函数的不足，而函数解析式具有计算精准的特点，可以弥补图像精准性不高的缺陷，通过两者的结合运用，可以有效解决问题。一般而言，在高中数学教学中应用数形结合思想方法，主要在一次函数、二次函数、三角函数等解题应用，同时，直线、圆锥曲线图形可以充分表达一些代数变化，对解题有着一定的帮助作用。比如，点M（x，y）是圆（x-2）2+y2=3上的任意一点，对（x-y）的最小值与最大值进行求取。

解析：设x-y=b，可以将此方程转变为y=x-b，将直线与圆相切，那么-b就是直线在y轴上的截距，如下图所示，b1就是（x-y）的最小值，b2就是（x-y）的最大值。

通过此例题的可知，在高中数学教学中，通过数形结合思想方法的运用，可以为解题提供便利条件，并且能够实现抽象知识与形象知识的有效转换，不仅培养了学生的数学思维，也增加了解题思路，对提高学生的数学成绩有着积极作用。

总而言之，在高中数学教学中，要想有效提高学生的数学成绩与解题能力，就要重视解题方法的运用。所以，在教学中，教师一定要向学生传授一些有效的解题方法，而数形结合思想方法就是一种非常适合的方法，可以拓展学生的解题思路，发散学生的解题思维，对培养学生的数学思维有着重要的意义，值得相关人士进行深入研究。

参考文献：

[1]范粤.高中数学教学中渗透数形结合思想应注意的几个问题[J].数理化学习，2014，（07）.

[2]刘永芳.“数形结合”思想在高中数学教学中的重要作用[J].读写算，2013，（30）.