局部柔度变化在管道裂纹定量识别中的应用*
何育民,高 攀,张小龙,申 鹏
(西安建筑科技大学机电工程学院 西安,710055)
局部柔度变化在管道裂纹定量识别中的应用*
何育民,高 攀,张小龙,申 鹏
(西安建筑科技大学机电工程学院 西安,710055)
局部柔度可描述结构上出现的裂纹,结构的模态参数将随着裂纹的扩展而改变,利用这一变化可辨识出裂纹发生的位置和深度。由此,建立了一种基于局部柔度变化的管道裂纹定量识别方法。该方法通过将管道结构沿径向离散为一系列依次嵌套的薄壁环,从而求得裂纹引起的局部柔度的变化规律,进而获得局部柔度与管道固有频率的特征关系,绘制裂纹管道的各阶固有频率曲面。采用实测前3阶固有频率去截取相应的固有频率曲面,获得各阶频率等高线,利用其交点定量诊断裂纹的位置与深度。实验结果验证了该方法的有效性。
故障诊断; 运输; 裂纹; 柔度; 固有频率
引 言
管道是包括铁路、公路、水运、航空运输在内的五大运输工具之一,在石油化工等生产中占有极其重要的地位,及时、准确地检测出管道的缺陷和隐患,对保证社会生产和生活以及人民的生命财产具有重要的实际意义。任何结构都可以看作是由质量、阻尼与刚度矩阵组成的动力学系统,一旦出现裂纹损伤,结构参数就随之发生变化,从而导致系统振动模态参数(固有频率、阻尼、振型)的改变。因此,模态参数的改变可视为结构早期损伤发生的标志,通过寻找模态参数与结构损伤的关系,利用结构损伤前后振动模态参数的改变来反映结构损伤的特征,可对结构裂纹进行诊断。近年来,基于振动的裂纹诊断方法已经取得了许多成果,Owolabi等[1]研究了梁结构中频率的变化在裂纹诊断中的应用。Papadopoulos等[2-4]讨论了模态参数在转子裂纹识别中的应用。李兵等[5-6]基于小波有限元,对悬臂梁结构和工字截面梁轨结构的裂纹损伤识别进行了研究。李洪升等[7]将频率变化平方比应用于管道损伤检测。崔之健等[8]采用模态分析的方法对管道损伤进行了仿真研究。Murigendrappa等[9-10]研究了充满液体的管道中出现裂纹时频率变化的规律。在这些研究中,通常采用扭转线弹簧模型描述裂纹引起的结构局部柔度变化,通过计算应力强度因子从而获得裂纹局部柔度或等效刚度。但是,其中大部分的研究工作集中在对实心矩形截面或者圆截面的杆梁结构的损伤识别上。由于管道结构不仅同实心结构一样承受着各种复杂外界载荷,而且是一种空腔的薄壁结构,内部通常还有流(气)体作用,裂纹扩展复杂,应力强度因子计算困难。因此,国内外有关管道裂纹引起的局部柔度的研究工作相对较少。Maniwadekar等[11]在研究管道裂纹识别技术时,为了克服应力强度因子计算的困难,提出了分别基于静变形和固有频率测量的实验方法来获得裂纹等效刚度。He等[12]将管道结构沿径向离散为一系列依次嵌套的薄壁管,借助已有的薄壁管应力强度因子公式求得管道结构的应力强度因子,从而提出一种裂纹局部柔度或等效刚度的计算方法。胡家顺等[13-14]进一步研究了横向裂纹的角度发生变化时局部柔度计算方法。利用这种计算方法,笔者研究了裂纹局部柔度的变化规律,通过对含有裂纹的管道结构进行动力学建模,采用正问题(裂纹结构数值建模)与反问题(通过振动测试和模态分析识别裂纹)相结合,建立了基于局部柔度变化的管道裂纹定量识别方法,可用于管道的无损检测。
1 裂纹辨识原理
对于管道结构而言,裂纹的出现改变了结构的固有频率。假设fr表示管道的第r阶固有频率,裂纹位置、深度和管道的固有频率之间存在如下关系
(1)
其中:β和α分别为裂纹的相对位置和相对深度。
裂纹辨识的正问题可看作是在函数关系式F已知情况下,通过裂纹参数β和α求解结构的固有频率fr。通过正问题的求解,即有限元建模,获得不同裂纹位置和深度组合时结构的前3阶固有频率,进而绘制出以裂纹相对位置β和相对深度α为自变量,裂纹结构固有频率为因变量的各阶固有频率曲面。
同样,若已知结构的实测固有频率,求解裂纹位置和深度的问题,即裂纹辨识中的反问题可用如下数学关系式描述
(2)
2 裂纹局部柔度的计算
结构上出现的裂纹可以引入一个局部柔度或等效刚度来描述,柔度或刚度的大小以及结构的动力学特性将随着裂纹的扩展而改变,利用这一变化可辨识出裂纹发生的位置和深度。为了描述裂纹引起的结构局部柔度变化,将裂纹等效为扭转线弹簧。文献[2]将管道结构沿径向离散为一系列依次嵌套的薄壁管,通过求解每个薄壁管的应力强度因子,可以得到整个管道的应力强度因子,进而求得裂纹局部柔度或等效刚度。
Kt求解步骤如下:假设管道的内、外半径分别为Ra和Rb,考虑管道上存在一个横向裂纹,裂纹深度为h,裂纹截面如图1所示。假设将管道沿径向将壁厚均匀离散为n个薄壁管,通过求解每个薄壁管的应力强度因子,可以得到整个管道的应力强度因子KI,进而求得裂纹等效刚度。当n足够大时,KI的计算能够获得很高的精度。第i个薄壁管裂纹横截面如图2所示。
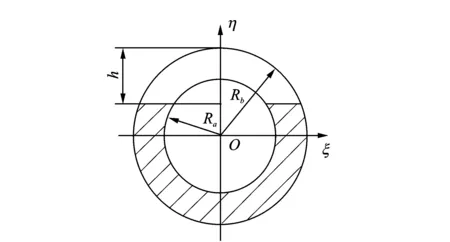
图1 管道裂纹横截面
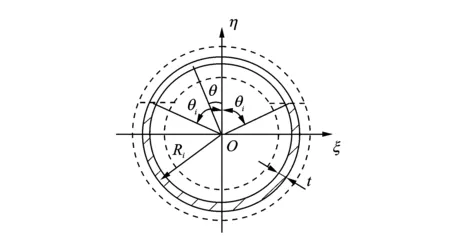
图2 第i个薄壁管裂纹横截面
将第i个薄壁管的应力强度因子记为Ki[15],Ki可以根据下式计算
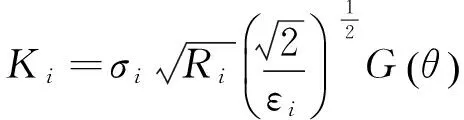
(3)
(4)
(5)
(6)
其中:t为薄壁管的壁厚;Ri为第i个薄壁管的内、外半径平均值;θ为角度坐标;M为管道裂纹两端的弯矩;Ii为第i个薄壁管横截面的惯性矩;I为管道横截面的惯性矩。
第i个薄壁管的应变能为
(7)
其中:θi为第i个薄壁管裂纹的张开角;θi=arccos((Rb-h)/Ri);Ji为第i个薄壁管的应变能密度函数。
总应变能为
(8)
U表示在弯矩M作用下裂纹管道的总应变能。根据卡式第二定理,U对于某一载荷的变化率就等于与该载荷相应的位移,故有
δm=∂U/∂M
(9)
其中:δm为与M相应的位移。
δm对M进行求导,可得到裂纹附加柔度cm和裂纹等效刚度Kt
Kt=1/cm
(11)
3 裂纹的出现与固有频率的变化规律
3.1 固有频率的计算
管道结构一旦出现裂纹损伤,就会导致系统振动模态参数(如固有频率)的改变,这些参数的改变可以视为结构发生损伤的标志。因此,需要研究裂纹的出现与固有频率的变化规律。假设管道左右两端简支,管道长度L=1.6 m,内径Ra=0.061 m,外径Rb=0.073 m,弹性模量E=2.06×1011N/m2,材料密度ρ=7 348.9 kg/m3,泊松比μ=0.3。以管道左端为坐标原点,裂纹位于l处且深度为h,β=l/L和α=h/D分别表示裂纹存在的相对位置和相对深度。
为了描述裂纹引起的结构局部柔度变化,将裂纹等效为无质量的扭转线弹簧。在采用有限元方法构造裂纹单元时,根据裂纹处的连接条件,左右两端节点的挠度值相等,转角存在一个角度差。裂纹单元刚度矩阵Ks为
(12)
裂纹单元质量矩阵为零矩阵,将管道的无裂纹部分的单元刚度、质量矩阵和裂纹单元的刚度、质量矩阵进行组装,从而获得总刚度矩阵K及总质量矩阵M,管道的固有振动特征方程为(横向裂纹故障与管道固有频率的特征关系)
(13)
其中:K为系统整体刚度矩阵;M为系统整体质量矩阵;ωr为系统固有频率;k为裂纹等效刚度;β为裂纹相对位置。
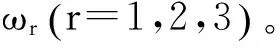
3.2 固有频率随裂纹位置和大小变化的规律
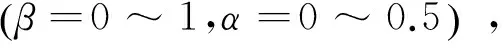
图4给出了管道在不同裂纹位置时前3阶固有频率随着裂纹深度变化的关系曲线。图5描绘了不同裂纹深度时前3阶固有频率随着裂纹位置变化的关系曲线。曲线变化规律如下:
1) 含裂纹结构的固有频率都小于无裂纹时的固有频率,即裂纹的存在减小了结构的固有频率;
2) 当裂纹位置确定时,裂纹结构各阶模态的固有频率随着裂纹深度的增大而逐渐减小;
3) 裂纹位置为某阶模态的节点时,随着裂纹深度的变化,该阶模态的固有频率值变化很小,即裂纹深度的变化对于该阶模态的固有频率值影响很小。
4 实验研究
在测量结构前3阶固有频率时,选取力锤作脉冲激励源,数据采集与分析系统为Sony EX,用Polytec激光测振仪拾取脉冲响应信号,采用快速傅里叶变换(FFT)和频谱细化技术对响应信号进行频谱分析,提取结构前3阶固有频率。实验对象几何参数、力学参数如上所述。裂纹测试原理如图6所示。管道上的裂纹通过在数控线切割机上采用直径0.18 mm的钼丝加工而成。
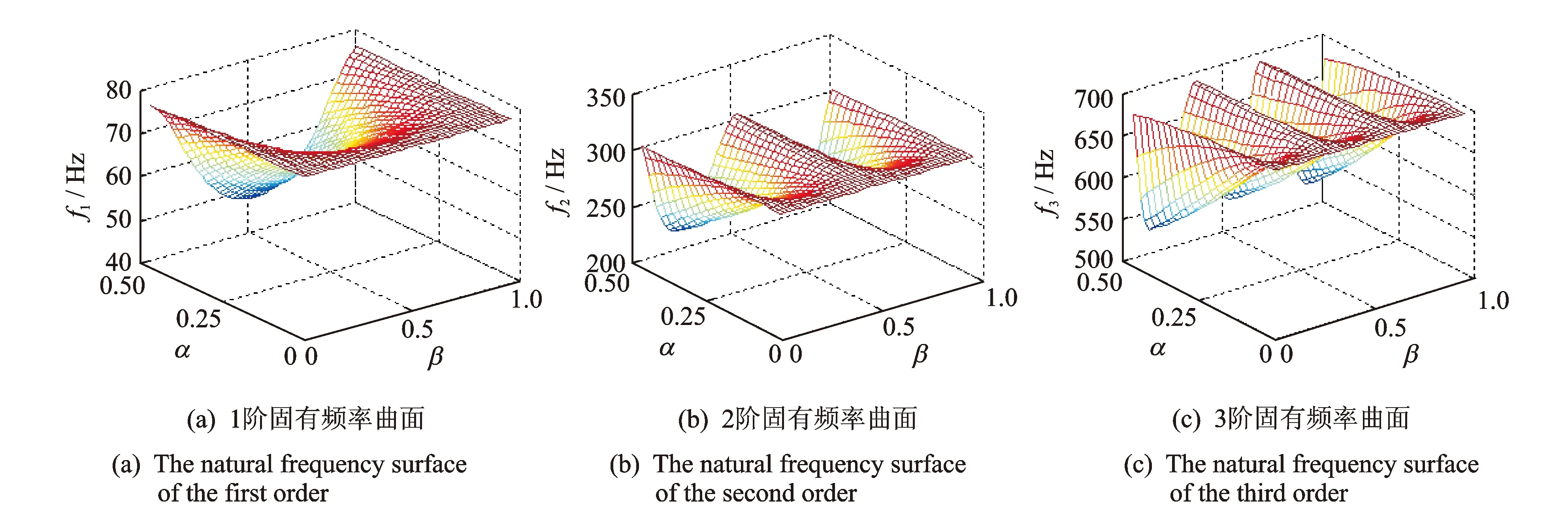
图3 不同裂纹位置和深度的固有频率曲面
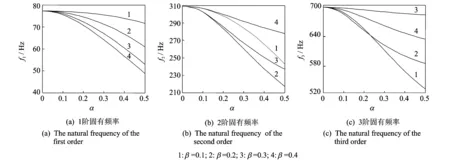
图4 不同裂纹相对位置时裂纹相对深度对结构固有频率的关系曲线
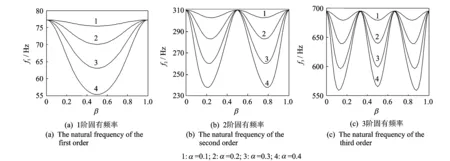
图5 不同裂纹相对深度时裂纹相对深度对结构固有频率的关系曲线
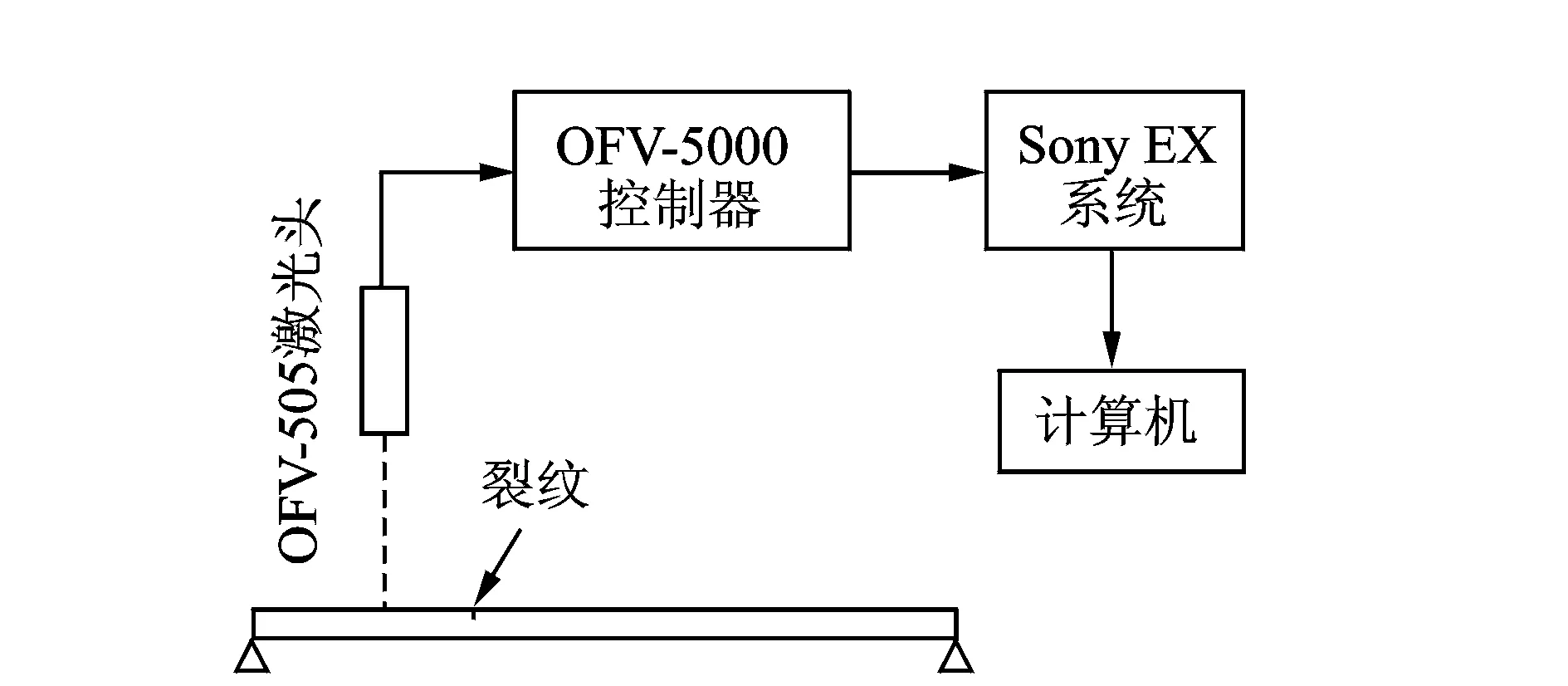
图6 测试原理图
4.1 模型修正
在大多数情况下,如果直接采用测试的前3阶固有频率作为反问题的输入,不能得到正确的裂纹定量诊断结果,其原因在于建立的数值模型与实际结构之间不完全一致,如阻尼、支撑条件、试件的材料特性(材质、厚度、长度)以及加工误差等,为此需要对数值模型进行修正,以提高识别准确性。考虑到数值模型与实际结构的误差对不同模态的影响,笔者采用了一种模态修正系数cr,r=1,2,3,对数值模型的前3阶模态分别进行修正。式(1)、式(2)描述了结构固有频率与裂纹的位置和深度的关系,经过修正的式(1)、式(2)为
(14)
(15)
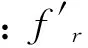
4.2 裂纹定量诊断
根据式(12),可以计算出在修正的模型下结构不同裂纹工况的前3阶固有频率,由此建立诊断数据库,绘制裂纹结构的各阶固有频率曲面。然后,将实测频率作为反问题的输入绘制频率等高线,3条等高线的交点(以三交点构成的三角形形心)可以指示裂纹存在的位置和深度。在实验中,管道两端的支撑均为简支,管道的几何形状和边界条件完全对称。因此,利用频率等高线的交点进行裂纹识别时,有两个完全对称的交点(当裂纹位于结构中心时,两个交点重合,只存在一个交点),可以根据裂纹所在的一端进行识别。表1给出了4种工况对应的实际裂纹参数,图7为4种工况下辨识裂纹位置和深度的频率等高线图,裂纹辨识结果见表2。表2中裂纹位置和深度相对误差计算公式分别为
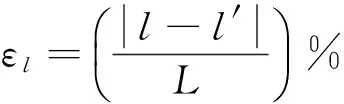
(16)
(17)
其中:l′为裂纹识别位置;h′为裂纹识别深度。
表2给出了4种工况下裂纹辨识的结果,裂纹位置的相对误差不超过4%,裂纹深度的相对误差不超过11%,结果验证了基于频率等高线的裂纹定量诊断方法的有效性。使用这种方法,只需对整体结构或局部结构进行测试,不需逐点检测就可比较准确地确定管道结构损伤位置及大小。
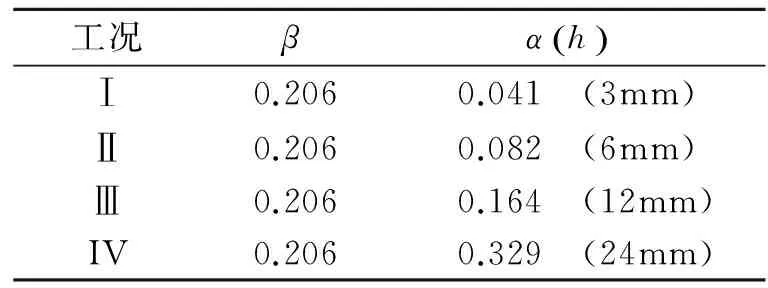
表1 裂纹的位置及深度
表2 裂纹位置及深度识别结果
Tab.2 The identification results of the size and location of a crack
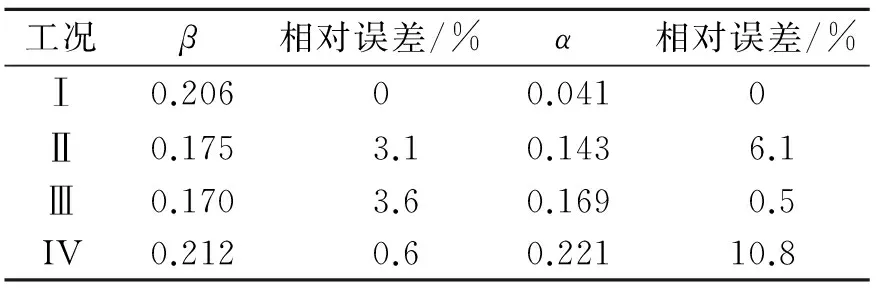
工况β相对误差/%α相对误差/%Ⅰ0.20600.0410Ⅱ0.1753.10.1436.1Ⅲ0.1703.60.1690.5IV0.2120.60.22110.8
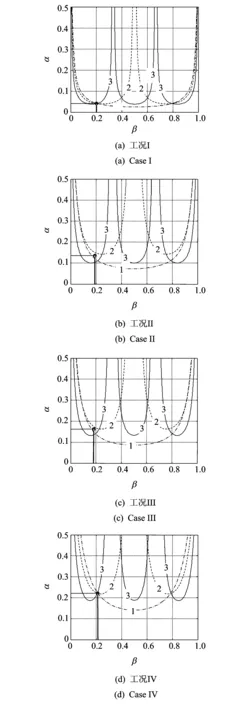
1:1阶固有频率; 2:2阶固有频率; 3:3阶固有频率
5 结束语
管道上裂纹的出现会引起结构局部柔度的变化,进而导致模态参数发生变化,笔者通过研究管道中裂纹引起的局部柔度的变化规律,分析了裂纹位置与大小对固有频率的影响,建立了一种基于局部柔度变化的管道裂纹定量识别方法。这种方法只需对整体结构或局部结构进行测试,不需逐点检测就可比较准确地确定裂纹位置及大小。该法使用简便,识别精度高,可用于管道裂纹的无损检测。实验结果验证了该方法的有效性。
[1] Owolabi G M, Swamidas A S J, Seshadri R. Crack detection in beams using changes in frequencies and amplitudes of frequency response functions[J]. Journal of Sound and Vibration, 2003, 265: 1-22.
[2] Papadopoulos C A. The strain energy release approach for modeling cracks in rotors: a state of the art review[J]. Mechanical Systems and Signal Processing, 2008, 22: 763-789.
[3] 刘长利,谢朋儒,周邵萍,等.基于有限元的呼吸裂纹转子动力学特性[J].振动、测试与诊断,2011,31(2):185-189.
Liu Changli, Xie Pengru, Zhou Shaoping, et al. Dynamics characteristics of rotor with breathing crack using finite element method[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(2): 185-189. (in Chinese)
[4] 刘长利,周邵萍,江君,等.双盘双呼吸型裂纹转子的非线性动力学特性[J].振动、测试与诊断,2012,32(S1):136-140.
Liu Changli, Zhou Shaoping, Jiang Jun, et al. Nonlinear dynamics analysis of double-disc rotor with two breathing cracks[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(S1): 136-140. (in Chinese)
[5] 李兵,陈雪峰,何正嘉. 基于小波有限元的悬臂梁裂纹遗传优化辨识[J].振动与冲击,2009,28(12):27-30.
Li Bing, Chen Xuefeng, He Zhengjia. Identifition of crack for cantilever beams based on wavelet finite element method and genetic algorithm[J]. Journal of Vibration and Shock, 2009, 28(12): 27-30. (in Chinese)
[6] 李兵,陈雪峰,何正嘉.工字截面梁轨结构裂纹损伤的小波有限元定量诊断[J].机械工程学报,2010,46(20):58-63.
Li Bing, Chen Xuefeng, He Zhengjia. Identifition of a crack in I-beams based on wavelet finite element method[J]. Chinese Journal of Mechanical Engineering, 2010, 46(20): 58-63. (in Chinese)
[7] 李洪升,陶恒亮,郭杏林.基于频率变化平方比的压力管道损伤定位方法[J].大连理工大学学报,2002,42(4):400-403.
Li Hongsheng, Tao Hengliang, Guo Xinglin. Damage locating method in stress ducting by frequency change square ratio[J]. Journal of Dalian University of Technology, 2002, 42(4): 400-403. (in Chinese)
[8] 崔之健,鲁明俊.基于应变模态分析的长输油气管线损伤检测仿真研究[J].机械,2006,33(8):55-57.
Cui Zhijian, Lu Mingjun. Identifying the damage of pipeline model based on the vibration model method[J]. Machinery, 2006,33(8): 55-57. (in Chinese)
[9] Murigendrappa S M, Maiti S K, Srirangarajan H R. Frequency-based experimental and theoretical with identification of multiple cracks in straight pipes filled fluid[J].NDT&E International,2004, 37:431-438.
[10]Dilena M, Dell′Oste M F, Morassi A. Detecting cracks in pipes filled with fluid from changes in natural frequencies[J].Mechanical Systems and Signal Processing,2011, 25: 3186-3197.
[11]Naniwadekar M R, Naik S S, Maiti S K. On prediction of crack in different orientations in pipe using frequency based approach[J]. Mechanical Systems and Signal Processing, 2008, 22: 693-708.
[12]He Yumin, Ye Junjie, Chen Xuefeng, et al. Discussion on calculation of the local flexibility due to the crack in a pipe[J]. Mechanical Systems and Signal Processing, 2009, 23(3): 804-810.
[13]刘朵,朱彤,胡家顺,等.贯穿裂纹管局部柔度的广义求解方法研究[J].中国海洋平台,2010,25(4):25-31.
Liu Duo, Zhu Tong, Hu Jiashun, et al. Study on generalized solution of the local flexibility of pipe with a through crack[J]. China Offshore Platform, 2010, 25(4): 25-31. (in Chinese)
[14]胡家顺,冯新,李昕,等.裂纹梁振动分析和裂纹识别方法研究进展[J].振动与冲击,2007,26(11):146-151.
Hu Jiashun, Feng Xin, Li Xin, et al. State-of-art of vibration analysis and crack identification of cracked beams[J]. Journal of Vibration and Shock, 2007, 26(11): 146-151. (in Chinese)
[15]Tada H, Paris P C, Irwin G R. The stress analysis of cracks handbook[M].3rd edition. New York: ASME Press, 2000:476.

10.16450/j.cnki.issn.1004-6801.2015.06.029
*国家自然科学基金资助项目(51075314,51175399);陕西省自然科学基础研究计划资助项目(2014JM7269)
2013-10-30;
2014-01-03
O1; TH17; TP306
何育民,男,1968年8月生,副教授。主要研究方向为机械设备状态监测及故障诊断。曾发表《Adaptive multiresolution finite element method based on second generation wavelets》(《Finite Elements in Analysis and Design》2007,Vol.43,No.6-7)等论文。
E-mail:He_yumin@163.com

