过程阻尼效应在钛合金铣削加工中的应用*

李 亮，赵 威，何 宁

(1.南京航空航天大学机电学院 南京，210016)(2. 盐城工学院机械优集学院 盐城，224051)



过程阻尼效应在钛合金铣削加工中的应用*

李 亮1,2，赵 威1，何 宁1

(1.南京航空航天大学机电学院 南京，210016)(2. 盐城工学院机械优集学院 盐城，224051)

对过程阻尼效应在钛合金铣削加工中的应用进了行研究。利用隐式龙格库塔法，计算典型钛合金材料铣削加工中干涉产生的侵入面积以及阻力，建立考虑过程阻尼效应的非线性铣削动力学模型，并基于此模型设计减振后角抑制颤振。计算与试验结果对比分析表明，所建模型能够较为准确地预测稳定性极限，过程阻尼效应可使低速区极限切深显著增加，而减振后角可使过程阻尼效应增强，进一步拓展稳定区域。

钛合金；铣削加工；颤振；过程阻尼；减振后角

引 言

钛合金一直被广泛应用于航空制造业，其具有比强度大、密度小、耐热性强以及耐低温等优良综合性能。用它制造飞机零部件，不仅可以延长飞机使用寿命，而且可以减轻重量，降低燃料消耗，从而大大提高其飞行性能。钛合金是一种典型的难加工材料，其导热性差，化学活性高，加工硬化严重，刀具寿命短，并且由于弹性模量小，切屑与前刀面的接触长度短，单位面积切削力大，加工过程中极易发生颤振。颤振给工件留下的斜状振纹往往需要手工去除，影响加工效率，严重的直接导致工件报废，甚至毁坏刀具。颤振问题是制约钛合金切削加工质量和效率的一大瓶颈。

控制颤振的方法一般均可归结为增加系统阻尼。切削系统阻尼可分为机床结构阻尼和由刀具后刀面与工件表面相互干涉而产生的阻尼，亦称为过程阻尼(process damping)[1-2]。过程阻尼是近年国际学术界的研究热点，被列为切削颤振中尚未解决的研究难点[3]。Turkes 等[4-5]基于刀具剪切角变化，以及后刀面和工件表面波纹之间干涉力的变化，建立了车削过程阻尼模型，对零阶频率法的临界切深表达式进行逆求解，识别过程阻尼。Huang 等[6-7]提出了包含切削阻尼的铣削动能模式，模式中包含剪切、犁耕两种切削机制，以及切削力大小及方向变动所产生的阻尼效应，建立线性周期性时变的铣削动能模型，并以该模型为基础，通过测试结构振动信号来辨识切削阻尼系数。Altintas等[8]通过一系列正交试验，识别动态切削力中的过程阻尼系数，该试验由快速伺服系统控制，使得刀具以预期频率和振幅振荡，但该试验系统较为复杂，工作量很大。文献[9]将正交车削的稳定性极限预测解析法和颤振试验相结合，利用二者获取的极限切深，直接辨识过程阻尼系数。基于此，又结合能量分析，获取侵入力系数，之后计算侵入面积和切削力，建立车削的稳定性分析模型。文献[10]系统分析了切削参数和刀具几何参数对过程阻尼的影响。文献[11-12]将其车削的过程阻尼建模方法推广到了铣削。Ahmadi等[13-14]基于小振幅假设，将过程阻尼等效为线性黏性阻尼，利用半离散法，计算铣削稳定性极限，该模型具有一定局限性，预测出的稳定性极限低于试验值。

目前，国际上对于过程阻尼的研究，车削远较铣削完善成熟。铣削是高间断性、时变的切削过程，侵入面积和过程阻力的计算远较车削困难。在现有文献中，切削稳定性分析均采用较为传统的线性模型[15-16]，未考虑过程阻尼，该模型在低速区会产生很大误差。对于钛合金加工来说，为保证刀具寿命，切削速度一般较低，这时如果还采用常用的线性模型，预测的极限切深远低于实际极限切深，势必会影响加工效率。过程阻尼的大小和刀具几何参数息息相关，鉴于此问题，笔者建立一考虑过程阻尼的非线性铣削动力学模型，利用隐式四阶龙格库塔法，计算典型钛合金材料加工时，刀具后刀面与工件振动波纹的侵入面积以及干涉阻力，预测稳定性极限，并且基于此模型，分析后角变化对稳定性极限的影响，设计减振后角来增强稳定性。最终结合试验得出结论，所建非线性模型能够较为准确地预测低速区的稳定性极限，所设计的减振后角能够有效增强过程阻尼作用，抑制颤振，改善加工质量，为解决钛合金铣削颤振问题提供一定理论支持。

1 过程阻尼形成机理

图1(a)为常用的二自由度铣削振动示意图[15]，刀具中心在机床整体坐标系下的振动位移分别为x和y,刀具振动给工件表面沿径向或切屑厚度方向留下了波纹。在切削加工中，如果颤振发生，振幅增大，这时后刀面与工件表面振动波纹发生干涉，形成侵入面积，阻力增大，会对颤振产生抑制作用。按照传统的线性模型，颤振发生以后，振幅是发散的，但是由于后刀面干涉形成的阻力，系统振荡不会发散，而是形成极限环，振动能量能够被控制，而相应的阻力被称为过程阻力。

对于过程阻尼的分析和计算，需要将振动转换到径向，即图1中的ur方向。刀尖径向的振动位移和振动速度为

(1)

其中：φj为切削刃的径向接触角，φj=Ωt；Ω为主轴旋转角速度。

当φj∈(φst,φex)时(φst,φex分别为刀具切入和切出时的接触角，本研究的工况为顺铣，φex为π)，刀具与工件有作用力产生，这时候需要计算ur和vr，其余时刻，这两个变量可置0。

(2)

其中：s为刀尖切向位移;vc为刀尖切削线速度。

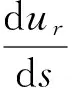
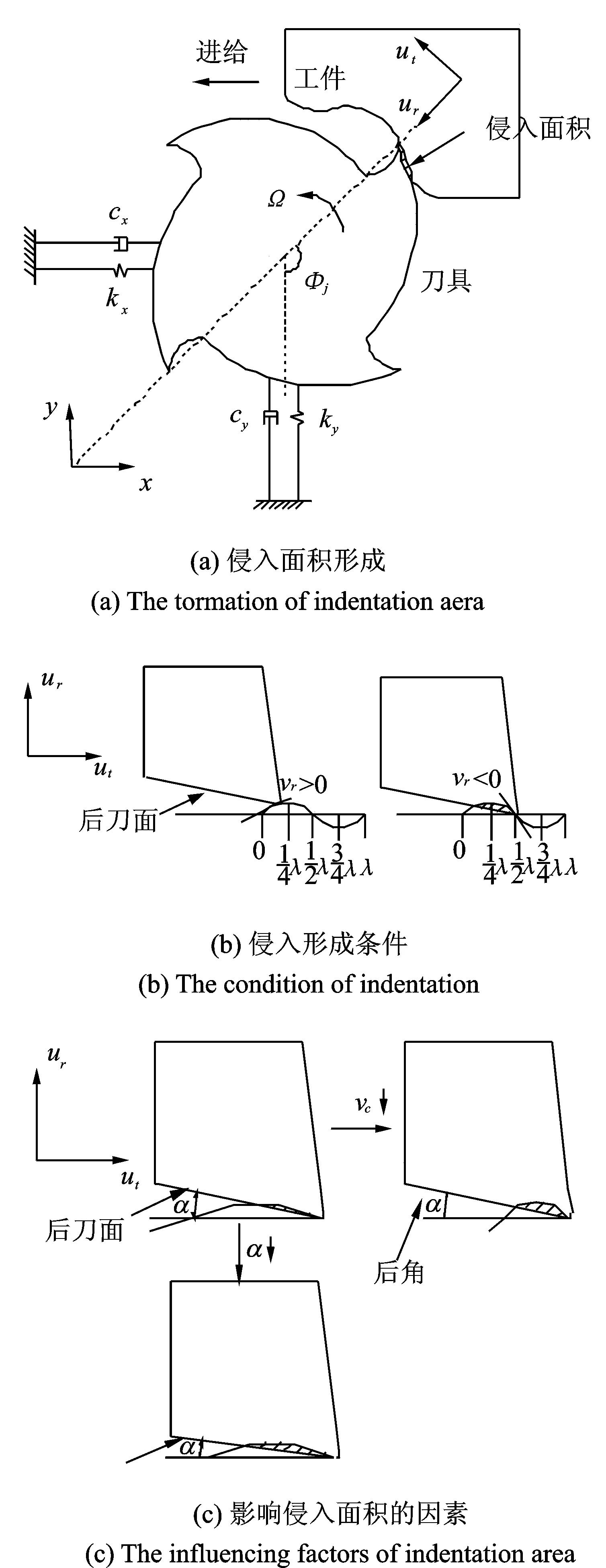
图1 过程阻尼形成机理示意图

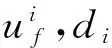
(3)

其中：Δs=vcΔt为相邻两时间点间的切向圆弧长；Δt为计算所取时间步长。

计算侵入面积，同时需要搜索判断刀具后刀面与振动波纹的交点，如图2(b)所示。当位置差di小于0时，即可判断后刀面与工件已加工表面脱离，交点前后的时间点记为n和n+1，dn>0，dn+1<0，这样，即可按照下式计算完整的侵入面积U(t,x,y)

(4)

ΔAn是按照三角比例关系获得，时间步长Δt取得越小，计算越精确。侵入体积V=apU(t,x,y)，ap为轴向切深。形成的侵入力Fp=KdV，摩擦阻力Fs=μFp，Kd为侵入力系数，μ为摩擦因数。

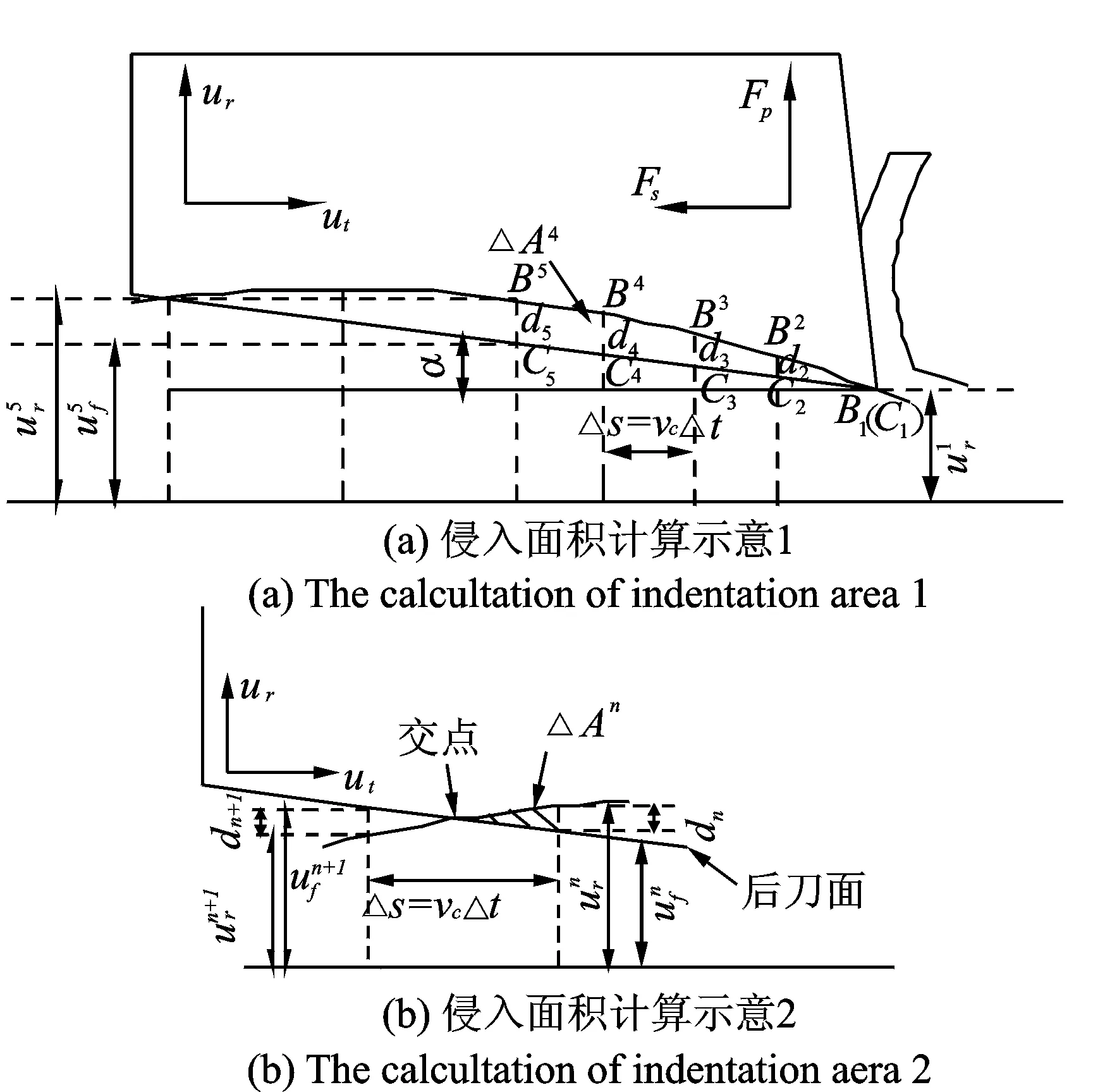
图2 侵入面积计算示意图

2 减振后角对过程阻尼的影响

由式(2)可以看出，后角减小，同样可使得过程阻尼增加。但在刀具设计中，后角减得过小，后刀面会与加工表面发生严重干涉，反而会降低加工质量。所以，在设计时往往采用一段过渡棱刃，如图3所示，其长度记为W。图中，改进后的刀具可采用2个后角，分别为后角1(α1)和后角2(α2)。其中α1设计得较小，起减振作用。

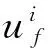
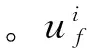
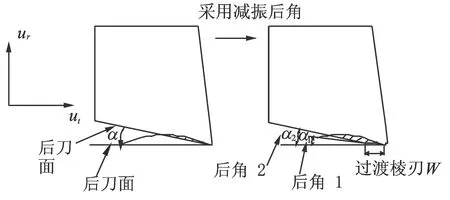
图3 减振后角对侵入面积影响示意图

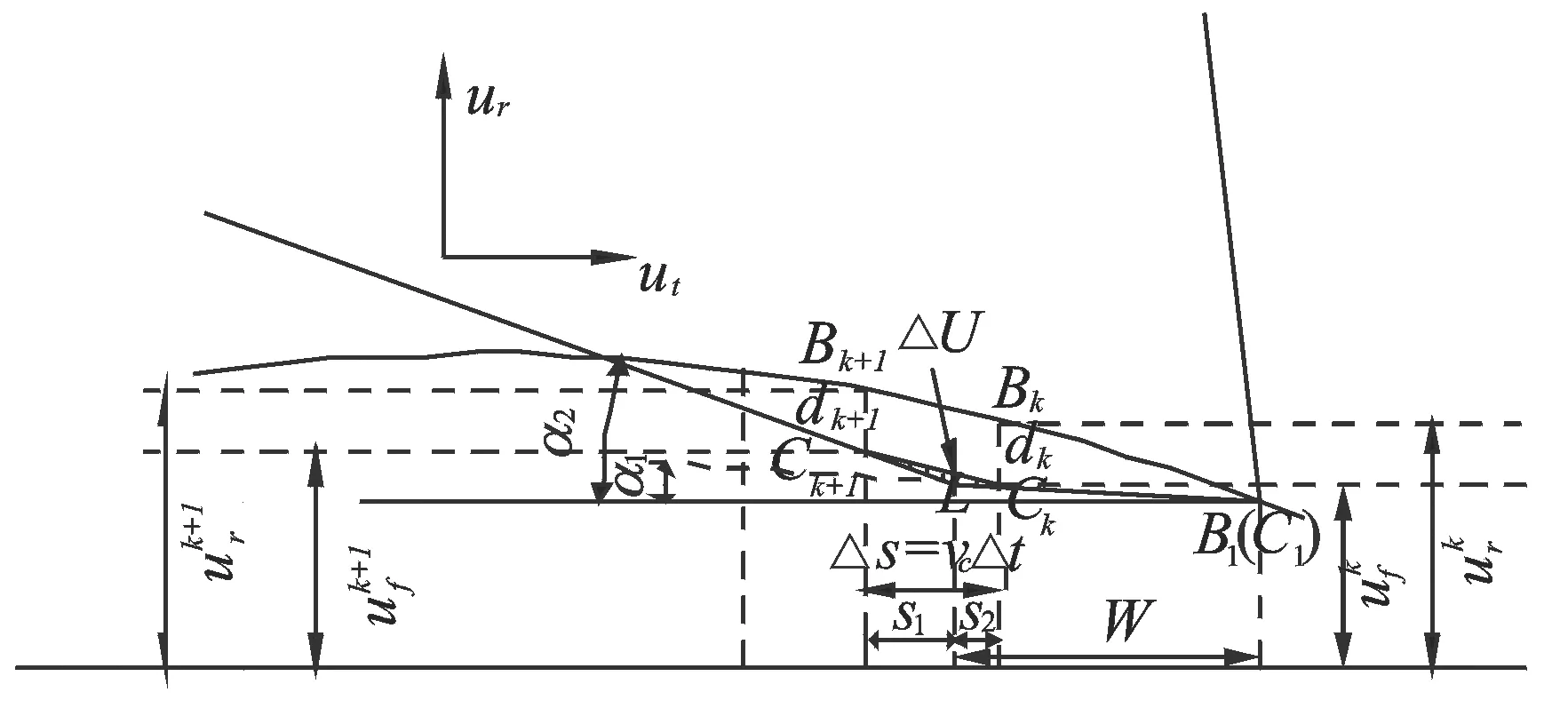
图4 侵入面积计算示意图(增加减振后角)

3 铣削动力学方程

将求得的过程阻力Fp，Fs,转换到整体坐标系下，叠加到切削力中，可得计入过程阻尼的动力学方程为

(6a)

(6b)

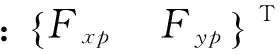
侵入面积U(t,x,y)是关于振动位移的非线性函数，式(6)具有很强的非线性。当刀尖径向振动速度vr满足式(2)，干涉发生时，φ为1，否则为0。(mx,my), (cx,cy), (kx,ky)分别为主轴-刀具系统的结构质量、阻尼、刚度参数(如图1(a)所示)，可通过模态试验获取。

作用于刀具的动态切削力为各个刀齿的切削力之和，为

(7)

其中：N为刀齿数。

单个刀齿的切削力[15]为

(8c)

Δx=x(t)-x(t-T)Δy=y(t)-y(t-T)(8d)

其中：Kt为切向力系数；Kr为径向力系数；hd为动态切屑厚度；ft为每齿进给量；T为刀齿周期。

当接触角φj∈(φst,φex) ，刀齿参与切削工件，g为1，否则为0。(x(t),y(t))为当前刀齿周期的振动位移，称为内调制；(x(t-T),y(t-T))为前一个刀齿周期的振动位移，称为外调制。内调制和外调制之间的相位差即为再生型颤振的根源[15]。对于钛合金来说，因为切削力系数Kt，Kr均较大[12]，所以更易发生颤振。

对于式(6)，可采用隐式四阶龙格库塔法求解，计算流程如图5所示，相关说明如下。

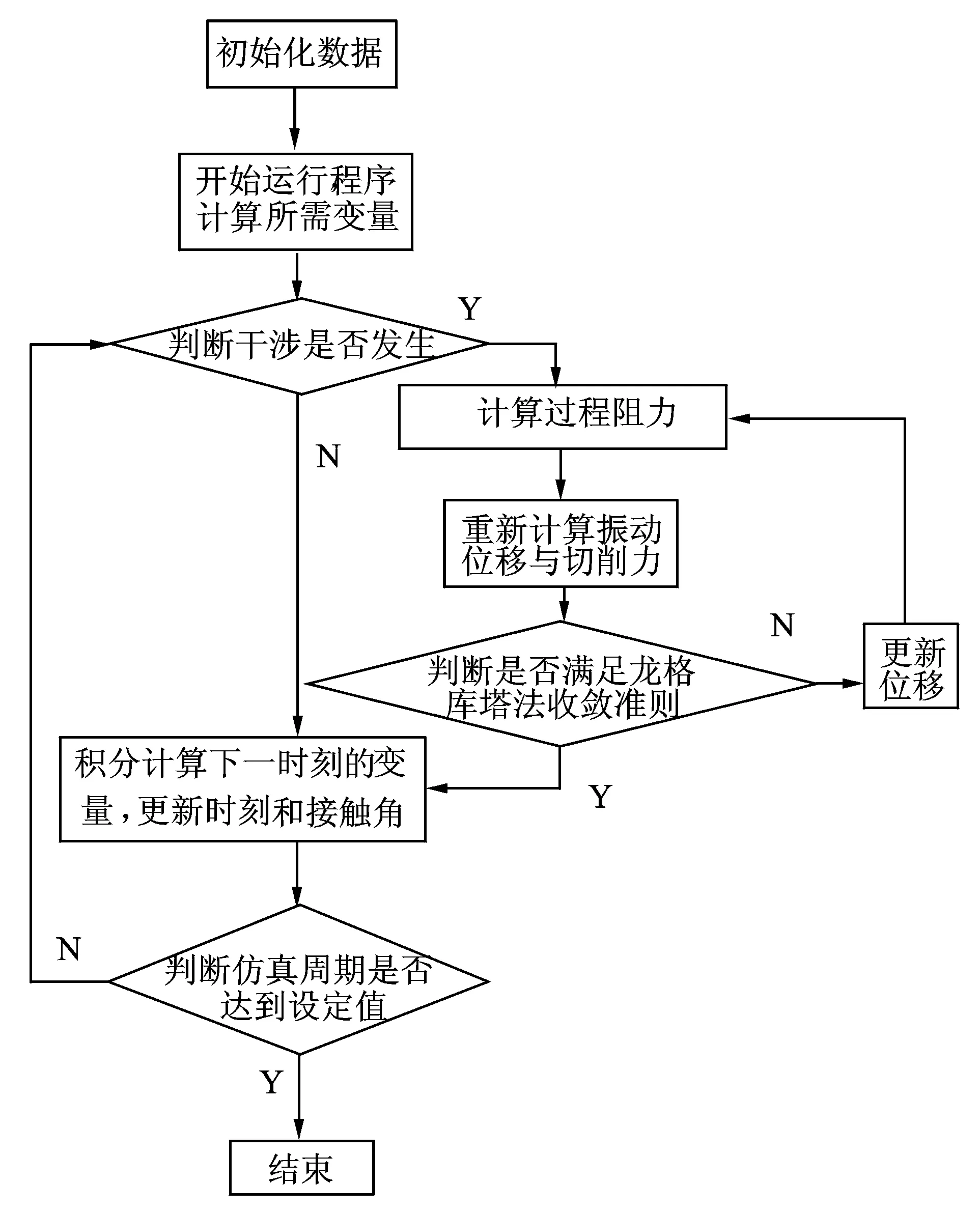
图5 计算流程示意图

1) 初始化数据。包括切削系统动力学参数、刀具后角、进给、刀具初始位置、切出切入角、切削力系数、需要的仿真周期、轴向切深、切削速度及计算步长。将刀具振动位移、速度和切削力置0。

2) 开始运行程序。所需变量包括刀尖振动位移x(t),y(t)，以及振动速度、加速度、切削力和动态切屑厚度hd。需同时进行坐标转换，计算径向振动位移xr(t),yr(t)，判断干涉是否发生。一般在最初的几个周期，振动位移比较小，干涉不会发生。

3) 判断干涉是否发生，即式(2)是否满足。干涉发生以后，同样按照上面提供的方法，计算过程阻力，重新解式(6)，更新位移。满足龙格库塔法收敛准则之后，记录该时刻的变量，再进行下一时刻的计算。

4) 在程序运行结束后，需要判断颤振是否发生。对于给定工况，得到足够的时域数据后，可以按照文献[17-18]提供的颤振判定法，设定阈值为η。最大动静态切屑厚度比hd,max/hs,max>η时，即可视为颤振发生。hd,max为最大动态切屑厚度，在给定切宽、转速和进给情况下，随着轴向切深增大而增大。hs,max为最大静态切屑厚度，在不考虑跳刀的情况下，最大静态切屑厚度即为每齿进给量ft。在给定切宽和转速下，逐步增大轴向切深，由该判定法确定稳定性极限。

4 计算与试验对比分析

为验证所提出的非线性铣削动力学模型，进行了计算和试验分析。计算是基于Matlab编程，阈值η设为1.1，按照图5所示流程图，求解式(6)，进行稳定性分析。式中的模态参数为：固有频率ωnx=2 077 Hz,ωny=2 061 Hz；模态阻尼比ζx=0.035,ζy=0.026；模态刚度kx=ky=1.66×107N/m。

模态参数通过模态试验获取，试验测出频响后，通过有理分式法识别模态参数，测试及拟合出的频响函数如图6所示。

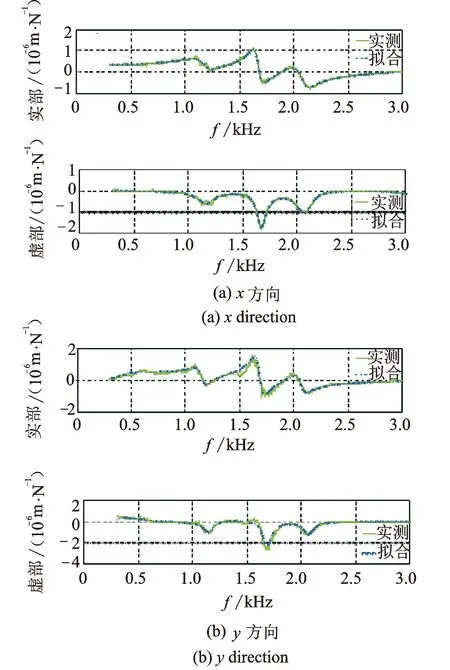
图6 实测和拟合频响函数

切削力系数为切向力系数Kt=2 000 MPa；径向力系数Kr=1 000 MPa，由铣槽快速标定法[17]获得。

过程阻力系数(钛合金Ti6AL4V的过程阻力系数标定见文献[12])：侵入力系数Kd=30 kN/mm3；摩擦因数μ=0.3。该组系数的获取难度较大，尤其是侵入力系数，需通过颤振试验结合振动能量分析来标定。

试验现场图如图7所示。主要设备如下：机床为Mikron UCP DURO800五坐标加工中心；刀具1为整体硬质合金立铣刀，全长为125 mm，悬长为70 mm，刃长为30 mm，直径为12 mm，4齿，后角为9°；刀具2(增加设计减振后角)的后角α1为4°，α2为9°，过渡棱刃长W=60 μm，其余参数与刀具1相同；传感器的测振由压电加速度传感器(PCB式)完成，测试工件振动；测声由BSWA传声器MP201完成；工件为钛合金材料Ti6AL4V；数据采集卡为NIUSB9233。

图7 铣削试验现场图

刀具的设计如图8所示。试验的主轴转速为500～4 000 r/min，在相同的转速下，切深每次均取1,3,5,7,9 mm，切宽为1 mm，进给为0.06 mm/z，顺铣，雾气冷却。

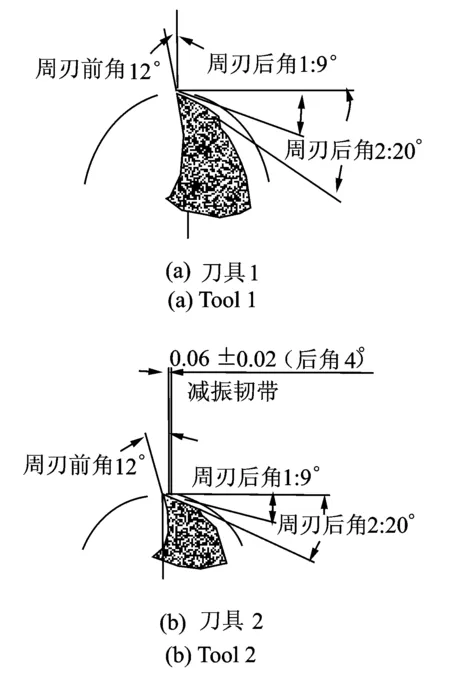
图8 两种刀具设计图

图9为刀具1计算和试验对比分析图。在计算模型中，分别计算了忽略和考虑过程阻尼非线性效应时的稳定性极限(式(6)如果不计过程阻力，即为周期系数线性方程)。从图9中可以看出，过程阻尼的作用很明显。按照传统的不计入过程阻尼的线性模型，在低速区很难有完整的稳定性叶瓣，稳定性极限很低[18-19]。计入过程阻尼之后，在转速低于2 kr/min(≈80 m/min)时，稳定区域明显扩大。

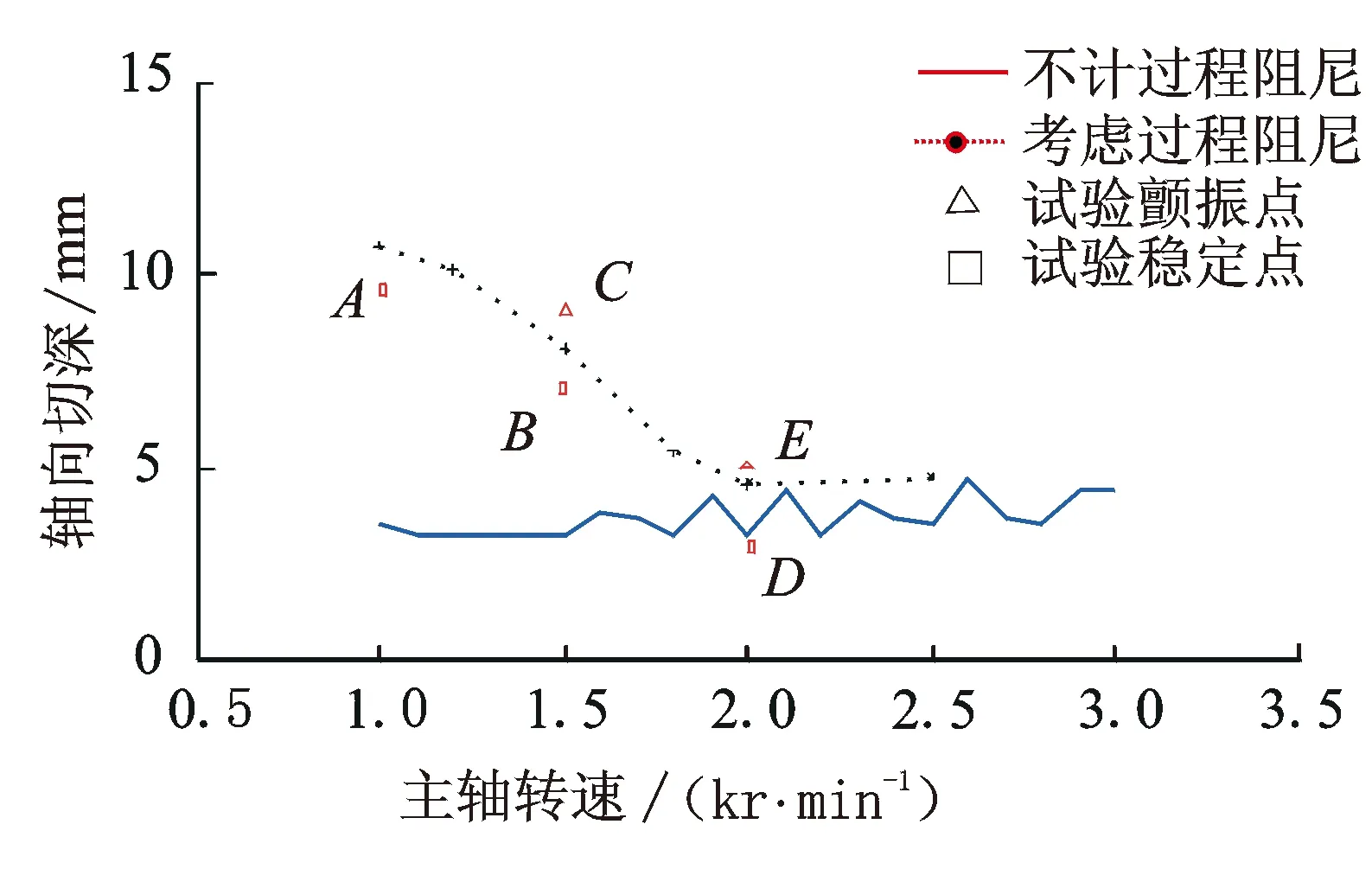
图9 计算与试验结果对比(刀具1)

图10为刀具1各试验点的谱分析结果，稳定性极限图是以2 061 Hz这阶模态来做分析进行绘制的。试验所采集的振动信号和声信号中，峰值较大的振动频率也多集中在2 000～2 500 Hz这个区间段，又因为转速较低，谱线很密，为看清频率成分，就截取2 000～2 500 Hz这个区间段进行谱分析。可以看出，在稳定点，频率成分主要都是主轴旋转频率(用★表示)和刀齿通过频率(用×表示)；而在颤振点，频率成分会发生变化，颤振频率(用○表示)会凸显出来。对于颤振频率，其相位β∈(π,2π)，且不与主轴旋转频率重合，属于hopf分叉[20]。从谱分析结果可以看出，试验结果和计算结果吻合较好。

图11为刀具2计算和试验对比分析图，图12为相应的试验点谱分析图。从图10可以看出，刀具采用减振后角后，过程阻尼效应到3 kr/min(113 m/min ) 后才消失。相对于刀具1，稳定区域和过程阻尼作用的转速范围明显扩充，减振后角的作用非常显著。

为更好地显示减振效果，可将刀具1的明显颤振点的工况( 2 kr/min, 7 mm )，同时用刀具2进行试验，来观察减振效果。图13(a)为刀具1的振动信号谱分析结果，其中颤振频率很突出；图13(b)为刀具2的振动信号谱分析结果，其中颤振频率已经基本消失，主要频率成分都是强迫振动成分，且峰值远小于刀具1的峰值，刀具2的减振效果非常显著。 从图14可以看出，刀具1加工时，工件表面有非常明显的斜纹，这是颤振发生的标志。刀具2加工时，表面非常光滑，振纹几乎消失，进一步体现了减振后角的作用。

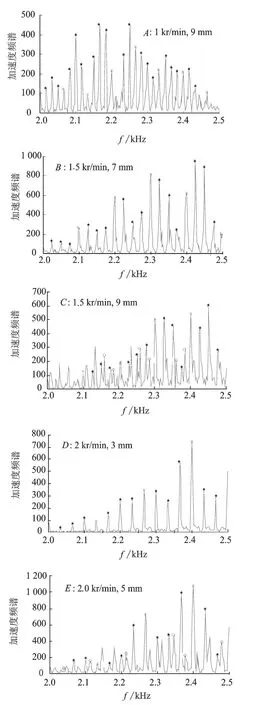
图10 试验点谱分析(刀具1)

试验和计算结果对比分析表明，笔者提出的计入过程阻尼的非线性模型能够较为准确地预测钛合金加工时低速区的稳定性极限，包括设计减振后角的刀具。过程阻尼能够使得低速区的稳定性极限显著提高，本研究工况刀具1在1 kr/min(≈40m/min)这样的钛合金常用切削速度下，稳定性极限能够由常规模型计算出的3mm提高到10 mm以上;而刀具2能够进一步增强过程阻尼效应，显著扩展过程阻尼作用的转速范围，完全体现了式(2)反映的规律。

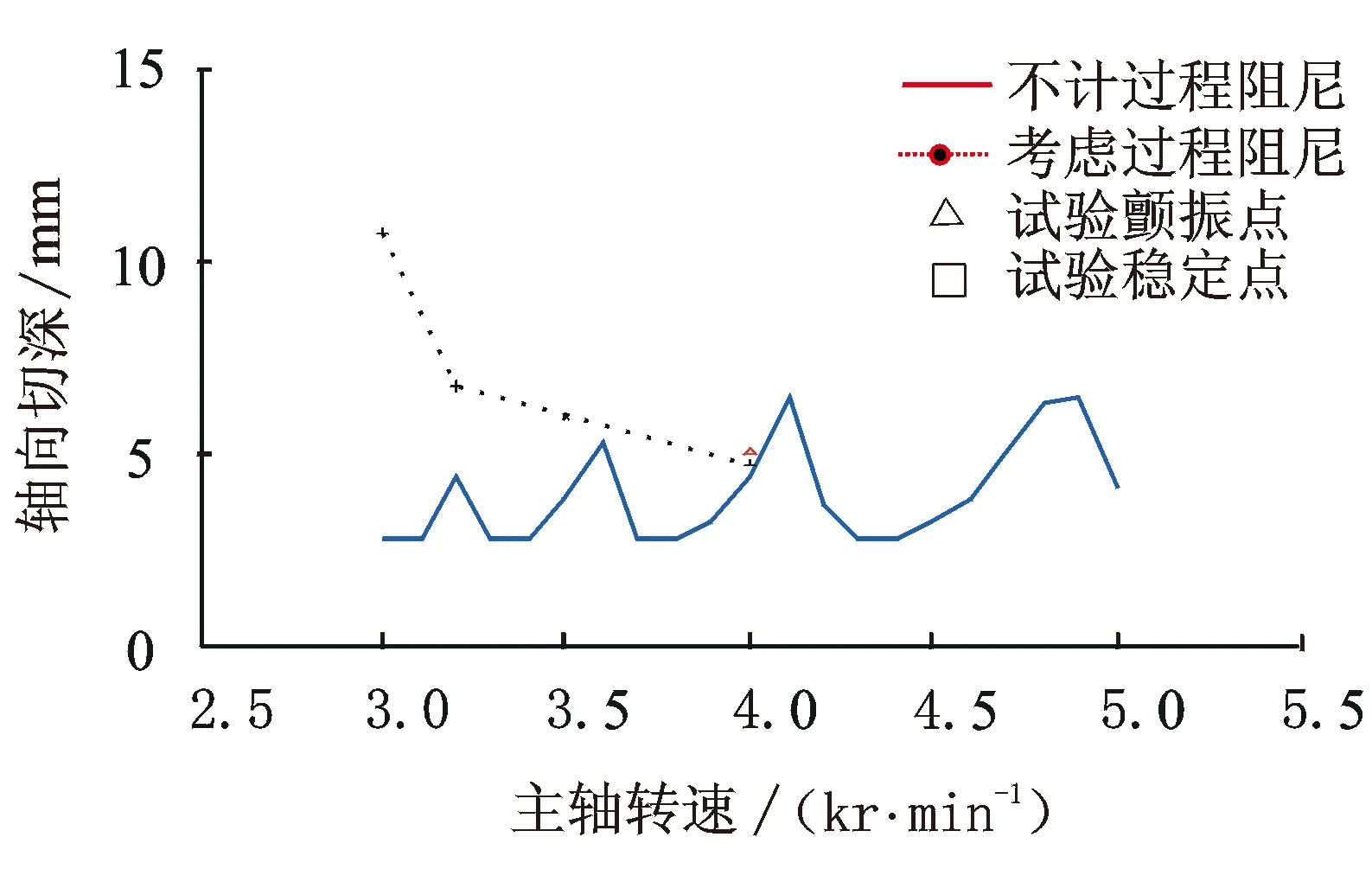
图11 计算与试验结果对比(刀具2)

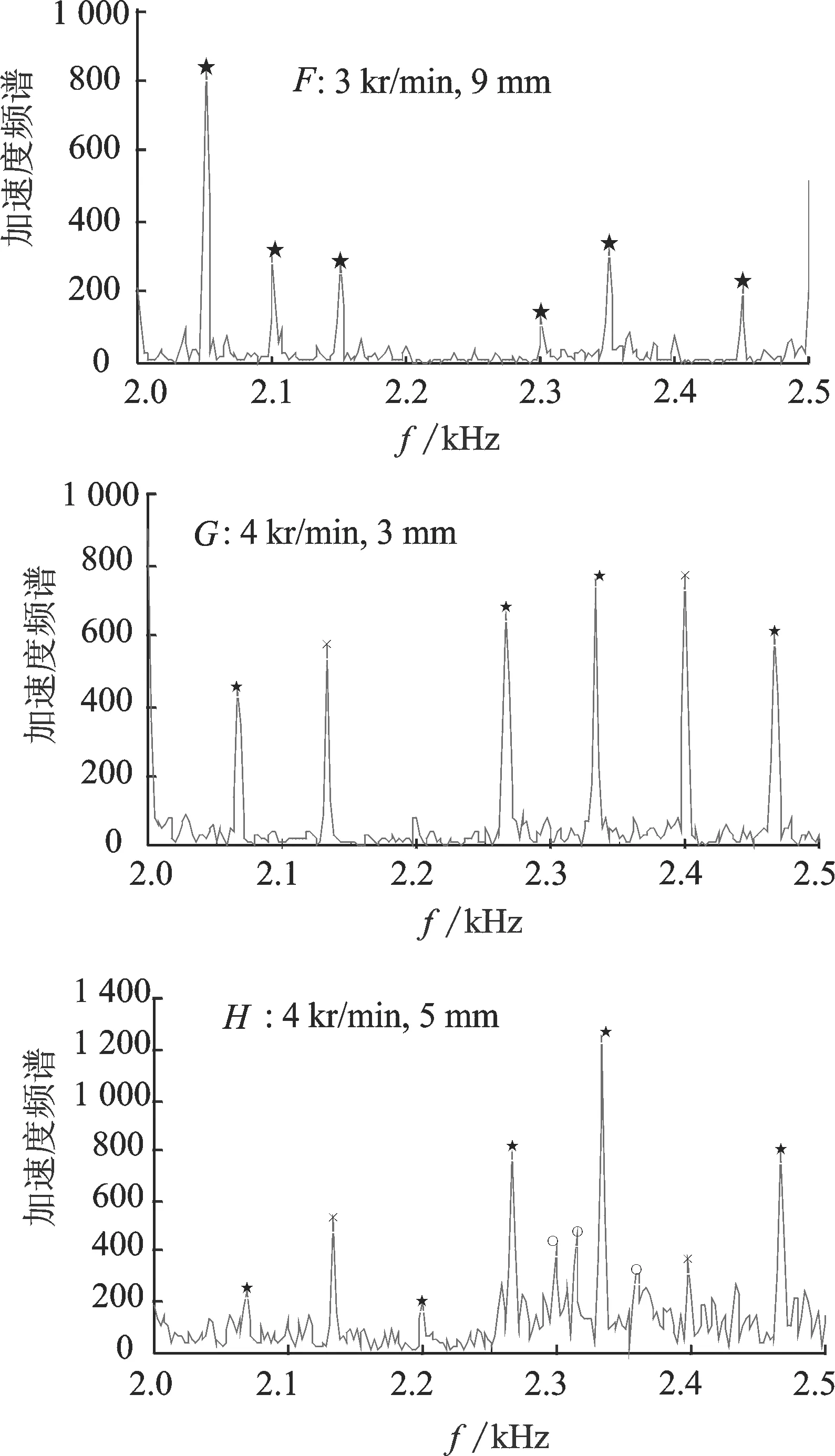
图12 试验点谱分析(刀具2)

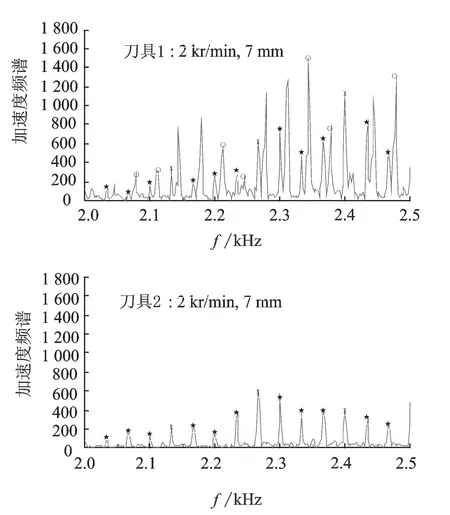
图13 振动信号谱分析结果对比

图14 工件加工表面质量对比

5 结束语

钛合金材料铣削中的颤振问题，是制约其制造加工效率的一大瓶颈。为保证刀具寿命，钛合金材料基本以较低速度进行切削。如果按照传统的线性模型，稳定性极限很低，依此模型选择切深将对效率非常不利，更难以为刀具设计提供依据。笔者针对此问题，建立了考虑过程阻尼的非线性铣削动力学模型，计算由干涉效应形成的侵入面积以及过程阻力，并通过时域仿真法计算稳定性极限。试验结果表明，所提出的计入过程阻尼的非线性计算模型，能够较为准确地预测钛合金加工时低速区的稳定性极限，包括减振后角对稳定性极限的影响。所设计的减振后角可进一步增强过程阻尼效应，扩展稳定区域，改善加工质量。

[1] Elbestawi M A, Ismail F, Du R, et al. Modelingmachining dynamic including damping in the tool-workpiece interface[J]. ASME Journal of Engineering for Industry，1994,116(4):435-439.

[2] Shawky A M, Elbestawi M A. An enhanced dynamic model in turning including the effect of ploughing forces [J].ASME Journal of Manufacturing Science and Engineering, 1997,119(1):10-20.

[3] Altintas Y, Weck M. Chatter stability in metal cutting and grinding[J].Annals of the CIRP, 2004,53(2):619-642.

[4] Turkes E, Orak S, Neseli S, et al. A new process damping model for chatter vibration[J]. Measurement, 2011,44:1342-1348.

[5] Turkes E, Orak S, Neseli S, et al. Decomposition of process damping ratios and verification of process damping model for chatter vibration[J]. Measurement, 2012, 45:1380-1386.

[6] Huang C Y, Wang J J J. Mechanistic modeling of process damping in peripheral milling[J]. ASME Journal of Manufacturing Science and Engineering,2007, 129:12-20.

[7] Huang C Y, Wang J，Junz J. Effects of cutting conditions on dynamic cutting factors and process damping in milling[J].International Journal of Machine Tools & Manufacture, 2011, 51:320-330.

[8] Altintas Y, Eynian M, Onozuka H. Identification of dynamic cutting force coefficients and chatter stability with process damping[J]. CIRP Annals-Manufacturing Technology, 2008, 57(1):371-374.

[9] Budak E, Tunc L T. A new method for identification and modeling of process damping in machining[J].Journal of Manufacturing Science and Engineering, 2009,131(5):1-10.

[10]Tunc L T, Budak E.Effect of cutting conditions and tool geometry on process damping in machining[J]. International Journal of Machine Tools and Manufacture, 2012,57: 10-19.

[11]Budak E, Tunc L T. Identification and modeling of process damping in turning and milling using a new approach[J].CIRP Annals-Manufacturing Technology, 2010, 59(1):403-408.

[12]Tunc L T, Budak E . Identification and modeling of process damping in milling[J]. CIRP Annals-Manufacturing Technology, 2013,135(2):1-12.

[13]Ahmadi K, Ismail F. Experimental investigation of process damping nonlinearity in machining chatter[J].International Journal of Machine Tools and Manufacture, 2010,50(11):1006-1014.

[14]Ahmadi K, Ismail F. Stability lobes in milling including process damping and utilizing multi-frequency and semi-discretization methods[J]. International Journal of Machine Tools and Manufacture, 2012,54-55:46-54.

[15]Budak E, Altintas Y. Analytical prediction of chatter stability in milling-part I:general formulation[J].Journal of Dynamic Systems, Measurement and Control, Transaction of the ASME,1998, 120(1):22-30.

[16]Altintas Y, Stepan G, Merdol D, et al. Chatter stability of milling in frequency and discrete time domain[J]. CIRP Journal of Manufacturing Science and Technology, 2008,1(1):35-44.

[17]Li Zhongqun, Liu Qiang.Solution and analysis of chatter stability for end milling in the time-domain[J].Chinese Journal of Aeronautics, 2008,21:169-178.

[18]Campomames M L,Altintas Y. An improved time domain simulation for dynamic milling at small radial immersions[J]. Transactions of ASME Journal of Engineering, 2003,125:416-422.

[19]林紫雄.间断切削的颤振稳定性研究[D].南京：南京航空航天大学,2011.

[20]宋清华.高速铣削稳定性及加工精度研究[D].济南：山东大学,2009.

10.16450/j.cnki.issn.1004-6801.2015.06.026

*国家自然科学基金资助项目(51475234)

2014-04-11；

2014-05-28

TH113; O327

李亮,男,1981年1月生,副教授。主要研究方向为切削颤振分析与试验。曾发表《汽车起动机减速轴冷挤压数值模拟分析》(《机械设计与制造》2010年第12期)等论文。 E-mail:jzlliang@163.com