局域波信息熵在高速自动机故障诊断中的应用*

潘宏侠, 都 衡, 马春茂

(1.中北大学机械与动力工程学院 太原，030051) (2.重庆青山工业有限责任公司 重庆，402761)(3.西北机电工程研究所 咸阳，712099)



局域波信息熵在高速自动机故障诊断中的应用*

潘宏侠1, 都 衡2, 马春茂3

(1.中北大学机械与动力工程学院 太原，030051) (2.重庆青山工业有限责任公司 重庆，402761)(3.西北机电工程研究所 咸阳，712099)

针对自动机工作时的短时冲击信号特征，首先，对其运动形态进行分解，截取与故障构件动作相对应的振动信号进行分析；其次，利用多层小波包分解截取信号，对其频率成分及能量分布进行研究；然后，将小波包分解后频带能量大的信号重构进行局域波分解，同时提取局域波奇异谱熵、边际谱熵和特征空间谱熵定量描述信号状态的时域、频域和能量的变化，并将其作为故障特征量；最后，利用遗传算法的全局寻优能力对支持向量机的参数进行优化，建立了遗传支持向量机(genetic algorithms-support vector machine,简称GA-SVM)模型，将提取的特征量输入其中进行故障分类识别，并将识别结果与空间穷尽搜索支持向量机(support vector machine,简称SVM)的识别结果进行对比。

局域波； 信息熵； 自动机； 遗传支持向量机； 小波包分解

引 言

高速自动机是小口径高炮的核心部件，其工作环境恶劣，运动规律复杂，在运动过程中经常伴随着激烈的撞击、摩擦、振动和跳动等，因此，其工作可靠性、各构件的裂纹及磨损逐渐成为火炮监测与诊断领域关注的焦点。自动机作为一个复杂的机械系统，当构件出现裂纹等故障时会影响其响应信号的频率能量特性，因此，笔者采用现代测试与分析方法，对自动机射击工作过程中的振动信号进行采集并应用信号处理方法提取对故障信息敏感的特征量，从而对故障加以识别。

为了使故障信息得以凸显，首先对自动机运动形态进行分解，截取与故障构件动作相对应的振动信号进行分析，并对截取信号进行多层小波包分解，计算各频带归一化能量，了解信号的频率组成及能量分布。自动机备件出现裂纹故障时，其频率、能量成分必然会发生变化，而频带能量高的信号所包含的故障信息量相对丰富，所以选择频带能量大的信号作为分析对象。局域波是基于信号波形的瞬时和局部特征，因此更加适合于非平稳信号的分析，而笔者研究的自动机振动信号正是包含大量冲击的非平稳信号。局域波可以自适应地将信号分为多个反应其模式组成的基本模式分量(intrinsic mode function,简称IMF)分量，并且各IMF分量经过Hilbert变换后得到的时频谱，能同时反应时域、频域信息。因此，用局域波对小波包分解后频带能量高的信号进行分解可进一步细分频谱，出现故障后的信号频率及能量变化会得到更加精确表现。反应复杂性测度的信息熵是对信号不确定性的定量描述，因此可应用信息熵理论对局域波分解后的信号提取特征量来反映信号的状态变化。

1 小波包频带能量分析

本次试验故障设置在闭锁片和枪机上，而闭锁片和枪机的主要动作是在闭锁行程和开锁行程完成的，因此，截取该两段行程对应的信号进行分析。具体故障设置如下：故障1在闭锁片闭锁斜面的圆角处，沿其半径方向设置2.0 mm深的裂纹槽，如图1所示；故障2沿经过闭锁片回转圆心且垂直于闭锁片内平面的方向设置1.5 mm深的裂纹槽，如图2所示；故障3在枪机左右两侧的圆角矩形窗后端的两对圆角上，沿圆角直径各成±45°切割1.5 mm深的裂纹槽, 如图3所示。

图1 故障1实物图

对通过试验采集的五连发射击振动信号截取测点一x向各故障状况后四发振动信号进行分析。考虑到采样频率较高,为204.8 kHz，为了能更清楚地了解信号频率分布情况，采用db4小波函数对截取信号进行6层小波包分解，将其分解到64个频带上，重构后计算归一化能量值，如图4～图7所示。

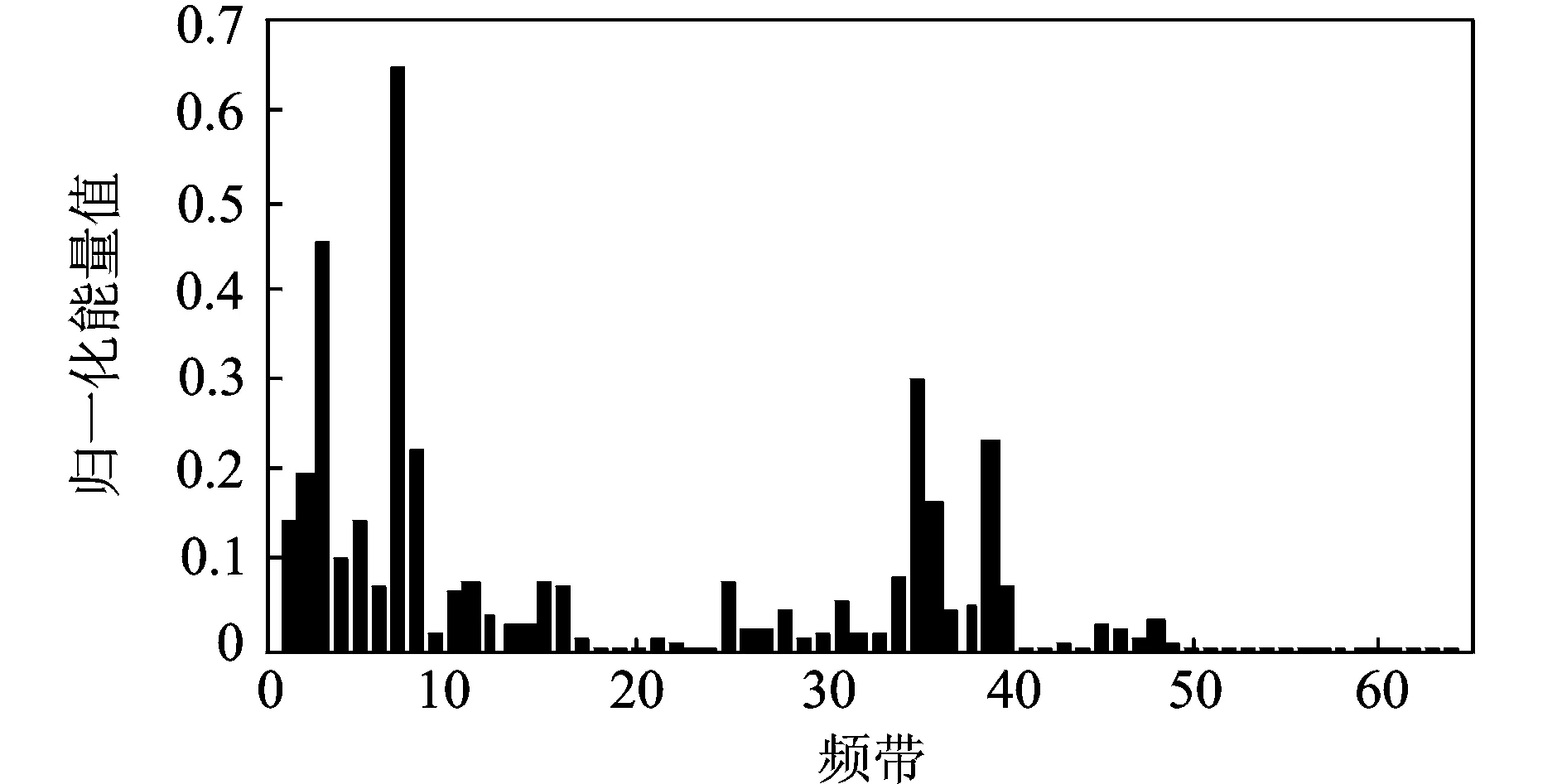
图4 五连发正常状况的6层小波包分解能量图

图5 五连发故障1的6层小波包分解能量图

图6 五连发故障2的6层小波包分解能量图

图7 五连发故障3的6层小波包分解能量图

从小波包分解归一化能量图中可以看出：4种状况下的能量都主要集中在低频部分(频带1～8，频率0～10 kHz);在频带35～40，虽也出现能量较大值，但相对低频部分要小的多，而4种状况的频带3和频带7的能量值均为峰值。对比4种状况的频带-能量图可发现，相互之间虽存在差别(如故障1频带7能量值相对要低一些，频带35上能量值也不同)，但并不明显，也无规律可言。为进一步对故障进行识别，提取频带3和频带7信号进行局域波分解。图8，9为五连发射击故障1小波包重构前后截取的信号时域图。

图8 五连发故障1的截取信号

图9 五连发故障1小波包分解重构信号

2 局域波信息熵特征提取

2.1 局域波奇异谱熵

奇异值具有好的稳定性是矩阵的固有特征，因此可被提取作为特征量。

假设信号X采样所得的M点一维时间序列表示为{X(i),i=1,2,…，M},采用延时嵌陷技术，嵌入维数为m，时间延迟为τ，根据Tekens嵌入定理[1]，将其嵌入到m×n维的相空间为

xk=[X(k),X(k+τ),X(k+2τ),…,

X(k+(m-1)τ)]T

(1)

其中：k=1,2,…，n；n=M-(m-1)τ。

轨道矩阵x=[X1,X2,…,Xn]代表相空间中n个坐标点，形成一条运动的轨迹[2]。对该矩阵进行奇异值分解，得奇异值δk,1≤k≤M-(m-1)τ。

奇异值分解需要延时重构相空间，而相空间重构质量很大程度上要受重构参数中嵌入维数和延迟时间的影响[3]，而这些参数的确定极为不便。局域波可将信号分解为一系列IMF分量，这些分量分别包含了从高到低不同频率成分、不同频带的信息，因此，将这些IMF组成初始特征向量矩阵

A=[h1,h2,…,hn]

(2)

对其进行奇异值分解，得到奇异值δi(1≤i≤n)。奇异值δi的大小是相应的模式在总的信号模式中所占比重的反映，而非零奇异值的个数是对信号频率成分组成多少的反映。{δi}是对信号在基本模式空间中的一种划分，称之为局域波奇异谱。由此可定义奇异谱熵为

(3)

其中：pi为在整个谱中第i个奇异值所占的比例分额，即第i个模式占的份额。

奇异谱熵反映了奇异谱划分下的系统振动能量的不确定性。信号越简单，熵值越小，能量越集中于少数几个模式；相反信号越复杂，熵值就越大，能量越分散。

2.2 局域波特征空间谱熵与边际谱熵

Hilbert时频谱H(ω,t)为基本模式分量在时频空间上的能量分布矩阵。由于矩阵的奇异值具有好的稳定性是矩阵的固有特征，因此对H进行奇异值分解，定义局域波特征空间谱熵为

(4)

其中：δi为H奇异值分解的第个奇异值;Hkj反映了局域波特征空间中局部能量分布的不确定性。

Hilbert边际谱h(ω)反映了信号的频率-能量结构，其含义与傅里叶频谱相类似。边际谱是对信号频域的一种划分，局域波边际谱熵定义为

(5)

Hbj刻画了信号的瞬时谱型结构情况。Hbj越大，则能量在整个频率成分上分布的越均匀，不确定性程度也就越大。由于局域波边际谱和时频谱中的频率具有瞬时意义，因此Hkj，Hbj与瞬时频率成分和振动能量在各模态的分布有关。

4种工况提取的部分特征量如表1所示。

表1 自动机五连发射击部分特征量

Tab．1 Characteristics of automaton shooting part five series

信号状态特征向量HkjHbjHqy正常8.12677.85387.69347.53491.59441.5688故障17.26817.51896.98147.20211.19071.2030故障27.97467.85067.33267.16960.84240.7401故障37.95018.10207.70567.68331.84661.7437

3 GA-SVM模型

(6)

其中：ek为松弛变量；C为惩罚系数。

利用拉格朗日乘子，将其转化为对偶最优化问题，则最终的分类决策函数为

(7)

SVM通过结构风险最小化原理来提高泛化能力，具有直观的集合解释和良好的分类能力，已广泛应用于故障诊断、控制理论等领域，但是SVM模型参数的选择仍未解决。SVM的优越性能需要选取合适的参数值才能体现，参数取值的好坏很大程度上影响了故障诊断的精度和效率[4]。支持向量机的参数选取通常采用参数空间穷尽搜索法，在实际问题中，因为很难事先知道最优参数所在的范围，所以这种方法不但很难精确地找到最优参数，而且采用遍选的方式效率也较低[5]。影响SVM性能主要有3个因素：分类间隔、对偶和核函数，而核函数更是其中的关键[6]。核函数参数σ主要影响样本数据在高维特征空间中分布的复杂程度，而误差惩罚因子的作用是在确定的特征空间中调节学习机的置信范围和经验风险的比例[7]。因此要提高SVM的分类识别能力，就需要选择合适的参数σ和c。

遗传算法是一种借鉴生物界自然选择和优化机制的高度并行、随机及自适应搜索的全局寻优算法，特别适合于传统搜索算法解决不好的复杂的和非线性问题[8]。遗传算法的初始群体是随机产生形成的,然后不断进化更新群体。适应度高的个体被直接复制到下一代群体中,其产生后代的概率较高。交叉和变异分别是以一定概率在染色体上进行基因交换或基因变异操作[9]。

支持向量机可较好地解决小样本局部极小值问题，这一特点正好解决了自动机故障特征量样本少的问题。遗传算法的优点是能够处理各种类型的目标函数和约束方便[10]，对所解的优化问题数学要求少，并且具有不依赖于特定求解模型的全局搜索能力，其优化过程中所需的较高计算量也可通过利用支持向量机的快速映射能力得到满足[11]。因此，可用遗传算法来优化支持向量机的参数，避免人为选择参数的盲目性。因此，笔者将二者结合，建立了GA-SVM模型以提高对故障的识别率。

4 自动机故障诊断试验

试验中各工况分别进行了一次五连发射击，考虑到第1发受初始因素影响，截取后4发的振动信号进行分析并提取特征值，这样每种状况包含4组样本。采用支持向量机进行分类，以每种状况的两组样本做训练样本，其余两组做测试样本输入支持向量机中进行识别。

为了获取最佳参数以提高故障识别准确率，分别建立了参数空间穷尽搜索SVM和GA-SVM分类识别模型。两种模型分别通过空间穷尽搜索和遗传算法来优化误差惩罚因子和核函数参数。空间穷尽搜索SVM模型中和的范围均设在[-210，210]范围内，以一定的间隔取值，然后选择使得期望风险上界最小的一组参数组合作为最优参数值。对于GA-SVM模型，设定群体规模m=50,最大遗传代数t=70，变量数目n=3，交叉概率pc=0．35，变异概率pm=0．02，产生初始种群，利用遗传算法自动进行全局搜索寻找最优参数。寻优过程中适应度函数随进化代数变化曲线如图10所示。将表1特征量作为训练样本分别输入利用空间穷尽搜索法和遗传算法得到最优参数的两种模型中，对其进行训练。相应的输出设为：正常→1；故障1→2；故障2→3；故障3→4。

图10 五连发状况遗传算法优化适应度函数曲线图

最后将测试样本输入两种模型中，得出诊断结果。自动机五连发射击测试样本特征量及诊断结果如表2所示。两种模型得到的最优参数及诊断正确率如表3所示。结果表明，两种模型对训练样本的识别率都能达到100%，但测试样本GA-SVM模型对故障识别率更高，准确率为87.5%，而空间穷尽搜索SVM识别率只有75%，说明了遗传算法相对传统的空间穷尽搜索方法可以更好地优化参数。

表2 自动机五连发射击测试样本特征量及诊断结果

Tab．2 Test sample characteristics and diagnosis results of automaton five series firing

信号状态特征向量HkjHbjHqy期望输出穷尽搜索SVM输出GA-SVM模型输出正常8.15057.81507.72277.52491.81231.3778111311故障17.24697.20677.02877.01290.90910.8338222222故障27.89687.81817.42397.13641.13330.7521333333故障38.07738.02507.79777.68252.27831.5842444141

表3 五连发射击两种诊断模型的最优参数及识别正确率

Tab．3 Optimal parameters and identification accuracy on the two diagnosis model of five series shooting

故障识别模型选取参数c,σ识别准确率/%训练样本测试样本穷尽搜索SVM1024, 102410075.0GA-SVM模型18.81, 228.5310087.5

5 结 论

1) 提出了应用小波包分解提取频带能量大的信号重构，并对其进行局域波分解进一步细化频谱，同时分别利用局域波奇异谱熵、边际谱熵和特征空间谱熵定量描述信号状态的时域、频域和能量变化的特征量提取方法。

2) 针对SVM的优越性能需要选取合适的参数值才能体现，而参数选择尚未得到有效解决，运用具有全局自动寻优能力的遗传算法对SVM进行参数寻优，建立了GA-SVM故障识别模型对故障进行分类识别。

3) 与空间穷尽搜索法寻优的SVM相比，GA-SVM具有更高的识别正确率。两种故障模型都具有较高的分类识别能力，体现了信息熵提取特征向量方法的可行性。为自动机从故障特征量提取到分类识别故障提供了一种有效的方法。

[1] Takens F. Detecting strange attractors in fluid turbulence[J]. Lecture Notes in Mathematics,1981, 898：363-381.

[2] 卢德林, 郭兴明. 基于奇异谱分析的心音信号小波包去噪算法研究[J]．振动与冲击, 2013, 32(18): 63-69.

Lu Delin, Guo Xingming. Wavelet packet denoising algorithm for heart sound signal based on singular spectrum analysis [J].Journal of Vibration and Shock, 2013, 32(18): 63-69. (in Chinese)

[3] 于大鹏，赵德有. 时延法相空间重构双参数联合估计方法研究[J]．大连理工大学学报, 2009,49(4): 540-544.

Yu Dapeng, Zhao Deyou. Study of dual parameters of delay-time coordinates phase space reconstruction[J]. Journal of Dalian University of Technology, 2009,49(4): 540-544. (in Chinese)

[4] Yuan Shengfa, Chu Fulei. Fault diagnosis based on support vector machines with parameter optimization by artificial immunization algorithm[J]. Mechanical Systems and Signal Processing, 2007,21:1318-1330.

[5] 陈法法, 汤宝平, 马婧华, 等. 基于遗传退火优化MSVM的齿轮箱故障诊断[J]. 振动、测试与诊断，2014, 34(4)：699-704.

Chen Fafa, Tang Baoping, Ma Jinghua, et al. Gearbox fault diagnosis based on multi-kernel MSVM optimized by genetic simulated annealing algorithm[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(4)：699-704. (in Chinese)

[6] 徐玉秀，杨文平，吕轩,等.基于支持向量机的汽车发动机故障诊断研究[J]. 振动与冲击,2013, 32(8)：143-146.

Xu Yuxiu, Yang Wenping, Lü Xuan, et al. Fault diagnosis for a car engine based on support vector machine[J]. Journal of Vibration and Shock, 2013, 32(8)：143-146. (in Chinese)

[7] 霍天龙, 赵荣珍, 胡宝权. 基于熵带法与PSO优化的SVM转子故障诊断[J]. 振动、测试与诊断，2011, 31(3)：279-284.

Huo Tianlong, Zhao Rongzhen, Hu Baoquan. Fault diagnosis for rotor systems based on entropy band method and support vector machine optimized by PSO[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(3)：279-284. (in Chinese)

[8] 李锋，汤宝平，刘文艺. 遗传算法优化最小二乘支持向量机的故障诊断[J]. 重庆大学学报,2010, 33(12)：14-20.

Li Feng, Tang Baoping, Liu Wenyi. Fault diagnosis based on least square support vector machine optimized by genetic algorithm[J]. Journal of Chongqing University, 2010, 33(12): 14-20. (in Chinese)

[9] Acevedo-Rodríguez J, Maldonado-Bascón S, Lafuente-Arroyo S, et al. Computational load reduction in deci-

sion functions using support vector machines[J]. Signal Processing, 2009,89(10)：2066-2071.

[10]Hajnayeb A, Ghasemloonia A, Khadem S E, et al. Application and comparison of an ANN-based feature selection method and the genetic algorithm in gearbox fault diagnosis [J]. Expert Systems with Applications, 2011, 38(8): 10205-10209.

[11]Jun Ye. Fault diagnosis of turbine based on fuzzy cross entropy of vague sets[J]. Expert Systems with Applications, 2009，36：8103-8106.

向 审 稿 人 致 谢

10.16450/j.cnki.issn.1004-6801.2015.06.025

*国家自然科学基金资助项目(51175480)

2014-12-17；

2015-06-03

TH17

潘宏侠,男，1950年10月生，教授、博士生导师。主要研究方向为机电系统检测诊断与控制。曾发表《基于局域波降噪和双谱分析的自动机故障诊断研究》(《兵工学报》2014年第35卷第3期)等论文。 E-mail：panhx1015@163.com