基于快速谱峭度图的EEMD内禀模态分量选取方法*

蒋 超，刘树林，姜锐红，王 波,2

(1.上海大学机电工程与自动化学院 上海，200072) (2.滁州学院机械与汽车工程学院 滁州，239000)



基于快速谱峭度图的EEMD内禀模态分量选取方法*

蒋 超1，刘树林1，姜锐红1，王 波1,2

(1.上海大学机电工程与自动化学院 上海，200072) (2.滁州学院机械与汽车工程学院 滁州，239000)

针对在总体平均经验模式分解(ensemble empirical mode decomposition，简称EEMD)的多个内禀模态分量(intrinsic mode function，简称IMF)中，如何选取出反应故障特征的敏感IMF的问题，提出一种基于快速谱峭度图的敏感IMF选取方法。由EEMD分解获得的一组无模式混淆的IMF，计算原信号及各个IMF的快速谱峭度图，选择每个快速谱峭度图中谱峭度最大值所处的频带作为参考频带，比较各个IMF的参考频带与原信号谱峭度最大值所处频带之间的从属关系，筛选出反应故障特征的敏感IMF，为后续故障诊断提供特征信息。将该方法应用于模拟仿真信号及滚动轴承滚动体故障信号，验证了方法的有效性。

总体平均经验模式分解； 快速谱峭度图； 冲击信号； 故障诊断

引 言

EEMD作为一种改进的经验模式分解(empirical mode decomposition，简称EMD)方法，它一方面保持了EMD分解的优良特性，即可根据信号特点自适应的将原信号分解为一系列IMF，另一方面又克服了EMD分解所存在的模式混淆问题，因此被广泛应用于非线性、非平稳信号的机械故障诊断信号处理方法中。与此同时，由于EEMD分解得到的IMF数量不可控，故障特征往往仅包含于一个或部分IMF中，而其他的IMF则大多可视为是噪声或干扰信号，所以，如何从EEMD分解的多个IMF中选取出反应故障特征的敏感IMF成为EEMD方法在故障诊断领域应用的重要问题。

有学者对上述问题进行了相关研究[1-2]。其中，苏文胜等[3]联合考虑了各IMF与原信号的互相关系数和各IMF的峭度值两个参考系数作为敏感IMF取舍的判决依据。雷亚国[4]提出一种利用故障状态信号与每个IMF的相关系数、正常状态信号与各个IMF的相关系数两组参考系数综合选择出敏感IMF的方法。鹏畅等[5]运用基于距离的度量因子将故障特征最敏感的IMF选取出来。张志刚等[6]采用灰色关联度与互信息方法相结合剔除EMD分解结果中的虚假分量。

笔者提出了一种基于快速谱峭度图的敏感IMF选取方法。首先，分别计算原信号及各个IMF的快速谱峭度图，获取每个快速谱峭度图中谱峭度最大值所处的频带范围作为各自信号的特征频带区间；然后，判断各个IMF谱峭度最大值所处的频带区间与原信号谱峭度最大值所处的频带区间两者之间的从属关系，筛选出反应故障特征的敏感IMF。因此，该方法使用了谱峭度最大值所处的频带范围这一双值特征区间系数，替代了谱峭度值、相关系数等一系列单值特征系数，并将敏感IMF选取过程中依靠人工经验取舍单值特征系数的问题简化为双值特征区间之间的从属关系问题，使敏感IMF选取方法更加易于实现。

1 基本理论

1.1 EEMD算法

为了克服EMD分解所产生的模式混淆现象,Wu等[7]在EMD分解算法的基础上，提出了一种利用高斯白噪声辅助的EEMD算法。它利用高斯白噪声所具有的频率均匀分布统计特性，通过每次给EMD分解信号中加入均值为零且幅值有限的不同高斯白噪声，使得信号在整个频带内的极值点间隔分布均匀，解决了不均匀极值点间隔导致的极值点上、下包络线拟合误差较大的问题，并对多次EMD分解的IMF进行总体平均计算以抵消所添加的噪声，从而获得一组无模式混淆现象的IMF。EEMD分解算法的具体流程如下:

1) 初始化总体平均次数M，并将白噪声序列加入到分析信号中;

2) 对加入白噪声后的分析信号做EMD分解;

3) 重复M次步骤1和步骤2，但每次添加幅值不同的白噪声序列;

4) 计算M次EMD分解所得到的相应IMF的总体平均，并将其平均值序列作为最终的IMF，即

(1)

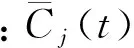
1.2 谱峭度方法

峭度指标作为时域分析中的一种无量纲参数指标，对信号的瞬时特征非常敏感[8]。随着频域分析理论和高阶谱理论的发展，谱峭度概念被Dwyer[9]提出，其基本思想是计算频域内每条谱线的峭度值，这样，谱峭度既能检测瞬态信号，又能够准确定位瞬态信号在频域中所处的位置。Antoni[10]在谱峭度理论研究的基础上，给出了谱峭度的定义，并将谱峭度方法应用于机械故障诊断领域中。

假设信号X(t)的激励响应为Y(t)，表示为

(2)

其中：H(t,f)为时变传递函数，解释Y(t)在频率为f处的复包络。

基于四阶谱累积量的谱峭度可定义为

(3)

其中:S2nY(f)为2n阶瞬时矩。

S2nY(f)定义为

(4)

谱峭度可进一步定义为

(5)

为显著减少谱峭度计算时间，使其能快速、广泛地应用于工程实际，Antoni[11]进一步提出了基于塔式算法的快速谱峭度图计算方法。在快速谱峭度图中，横坐标代表频率f，纵坐标则表示分解的层级K，频率分辨率为Δf=2-(K+1),图像上的颜色深浅表示各个f和Δf下的谱峭度值。

1.3 基于快速谱峭度图的敏感IMF选取方法

在利用EEMD分解方法对机械设备故障状况下的振动信号进行分析的过程中，对敏感IMF的选取方法研究已经达成两点共识：a.EEMD分解生成的一系列IMF数量不可控；b.振动信号故障特征往往仅包含于一个或部分IMF，而其他的IMF则大多可视为噪声信号或干扰信号。所以，为了凸显故障特征信息在重构信号中的表现形式，选取合适的特征参考系数成为敏感IMF选取方法的重点。

基于快速谱峭度图的敏感IMF选取方法，使用谱峭度最大值所处的频带范围作为特征频带区间，因为该频带范围是一对双值特征区间系数，不同于单值特征参考系数，所以在筛选敏感IMF时，可将权衡取舍单值系数的问题简化为多组不同双值区间之间的从属关系问题，避免了因单值参考系数不易区分而造成敏感IMF选取困难。具体步骤如下：

1) 对原始信号做EEMD处理，得到一系列IMF；

2) 利用快速谱峭度图原理，计算原信号及各个IMF的快速谱峭度图，获取相应的快速谱峭度图中谱峭度最大值所处的频带范围，并以该频带范围作为各个信号(包括原信号和多个IMF信号)的特征频带区间；

3) 判断每个IMF的谱峭度最大值所处的频带区间是否从属于原信号谱峭度最大值所处的频带区间，如果是则选为敏感IMF，否则剔除之；

4) 在步骤2和3中，若峭度值最大谱所处频率范围是整个频带，则取谱峭度次大值所处的频带范围作为特征频带区间，这是为了从频域范围内挑选出相对于其他频带更具有信号代表性的特征频带区间范围；

5) 若敏感IMF为多个，则对敏感IMF进行叠加，从而组合成反应故障特征的重构信号。

2 仿真实验

笔者模拟机械故障振动的仿真信号，运用所提出的敏感IMF选取方法对敏感IMF进行筛选，并对敏感IMF选取的结果进行分析，验证所提出方法的有效性。模拟仿真信号使用文献[12]中的仿真模型，考虑到机械设备零部件发生故障时，振动信号多以冲击信号的形式存在，针对冲击信号的特征提取亦是故障诊断信号处理的关键。同时，不同零部件的旋转频率通过一高一低两个正弦信号模拟。随着机械设备故障程度的加剧，传感器采集的振动信号平均幅值势必会变大，可通过一个幅值逐渐增加的趋势项进行模拟。因此，仿真故障信号主要由冲击成分、低频正弦成分、高频正弦成分、趋势项4种信号组合而成。

图1所示为仿真信号中的冲击成分、低频正弦成分、高频正弦成分、趋势项及上述4种信号的组合信号。运用EEMD分解对仿真信号进行处理，共分解得到12组消除了模式混淆问题的IMF，如图2所示。在分解结果中：c1对应了原始信号冲击成分；c5对应了原始信号高频正弦成分；c7对应了原始信号低频正弦成分；c12对应了原始信号中的趋势项。

图1 仿真故障信号及其组成

图2 仿真信号EEMD分解得到的12个IMF

图3 仿真信号的快速谱峭度图

图4 仿真信号IMF1的快速谱峭度图

图5 仿真信号IMF2的快速谱峭度图

图6 仿真信号IMF3的快速谱峭度图

根据所提出的敏感IMF选取方法，利用快速谱峭度图原理，计算原信号及各个IMF的快速谱峭度图。其中，图3为原信号的快速谱峭度图，谱峭度最大值所处的频带如箭头所指向的虚线框为(4 500,5 250)Hz，并选该频带范围为仿真信号快速谱峭度图的特征频带区间。图4～图6分别为IMF1，IMF2，IMF3的快速谱峭度图，其中：IMF1谱峭度最大值所处的频带范围是(4 500,5 250)Hz，该特征频带区间从属于仿真信号频带区间，故选取为敏感IMF；IMF2谱峭度最大值所处的频带范围为整个频带，按照方法步骤4选取谱峭度次大值所处的(0,1 500)Hz频带范围作为特征频带区间，因该频带区间不从属于仿真信号的频带区间，故舍去IMF2；同理，IMF3谱峭度最大值所处的频带范围同样为整个频带，故选取谱峭度次大值所处的(0,1 500)Hz频带范围作为特征频带区间，且该频带区间亦不从属于仿真信号的频带区间，故舍去IMF3；如此对剩余IMF进行选取，最终选取IMF1为敏感特征IMF。

为验证敏感IMF选取方法的有效性，可将选取的敏感特征IMF(IMF1)与故障仿真信号中的冲击成分做差值计算，如图7所示。可以发现，除了在每个冲击信号开始时刻点处存在较大偏差外，整个冲击过程中偏差均为较小值，该结果既说明了EEMD分解方法在抽取处理冲击信号过程中的优越性，也说明了敏感IMF选取方法的有效性。

图7 IMF1与仿真信号冲击成分的偏差值

3 实例研究

为进一步分析所提出的敏感IMF选取方法的可行性，以美国Case Western Reserve University电气工程实验室公开的滚动轴承滚动体故障数据为例，对该方法进行实例研究。具体参数如下：驱动端轴承型号为SKF6205，轴承转速为1 750 r/min，采样频率为12 kHz。理论计算得出的轴承滚动体故障特征频率为137.48 Hz。

图8包括了轴承滚动体故障的时域图、频域图和包络谱图。其中：时域图可以发现信号存在明显的周期性冲击现象；信号频谱分布范围较宽，故障特征频率微弱，无法拾取出故障特征；包络谱中滚动体故障特征频率明显，但也出现了如点划线框所示的干扰项。

图8 滚动体故障信号及其频谱图、包络谱图

对滚动轴承的滚动体故障信号做EEMD分解，其中，EEMD添加的白噪声幅值参数选取为原信号标准差的0.2倍，整体平均次数M选为100，共可得到15个IMF。以前5个IMF为例，计算各个IMF的谱峭度值和各个IMF与原信号之间的互相关系数，如表1所示，原信号的峭度值为3.596 9。从表1可以发现，各个IMF的峭度值均为较大值，特征参数分布没有明显的区分效果，因此，峭度值在该组实验数据分析中失去了参考价值。在各个IMF的互相关系数中，不同IMF之间的互相关系数大小差异程度明显，且IMF1与原信号之间的互相关系数远远大于其他IMF。因此，IMF1保留了更多的原信号信息，选IMF1为敏感IMF。

表1 前5个IMF的峭度值及其与原信号之间的互相关系数

Tab.1 The first five cross-correlation coefficients between IMF and original signal and the IMF kurtosis

IMF序列峭度值相关系数123453.53273.69313.98854.40143.75890.94060.06270.04340.03290.0175

采用所提出的敏感IMF选取方法，首先，计算原信号快速谱峭度图(见图9)，原信号快速谱峭度图中谱峭度最大值所处的频带范围如箭头所指向的虚线框，为(5 625,6 000)Hz，并将该频带范围选为滚动体故障信号的特征频带区间；然后，对故障信号EEMD分解后得到的15个IMF分别作快速谱峭度图，并从每个IMF的快速谱峭度图中找到谱峭度最大值所处的频带范围作为各个IMF的特征频带区间，如表2所示为前5个IMF快速谱峭度图中谱峭度最大值所处的特征频带区间参数，单位为Hz；最后，将各个IMF的特征频带区间参数与原信号特征频带区间参数进行对比，可知仅有IMF3的特征频带区间从属于原信号频带区间，故选IMF3为敏感IMF。

表2 前5个IMF的快速谱峭度图中谱峭度最大值的频带区间

Tab.2 The first five reference frequency band which determined by the maximum kurtosis in fast kurtogram

IMF序列特征频带区间12345(0,750)(3375,3750)(5625,5812.5)(937.5,1031.25)(3750,4500)

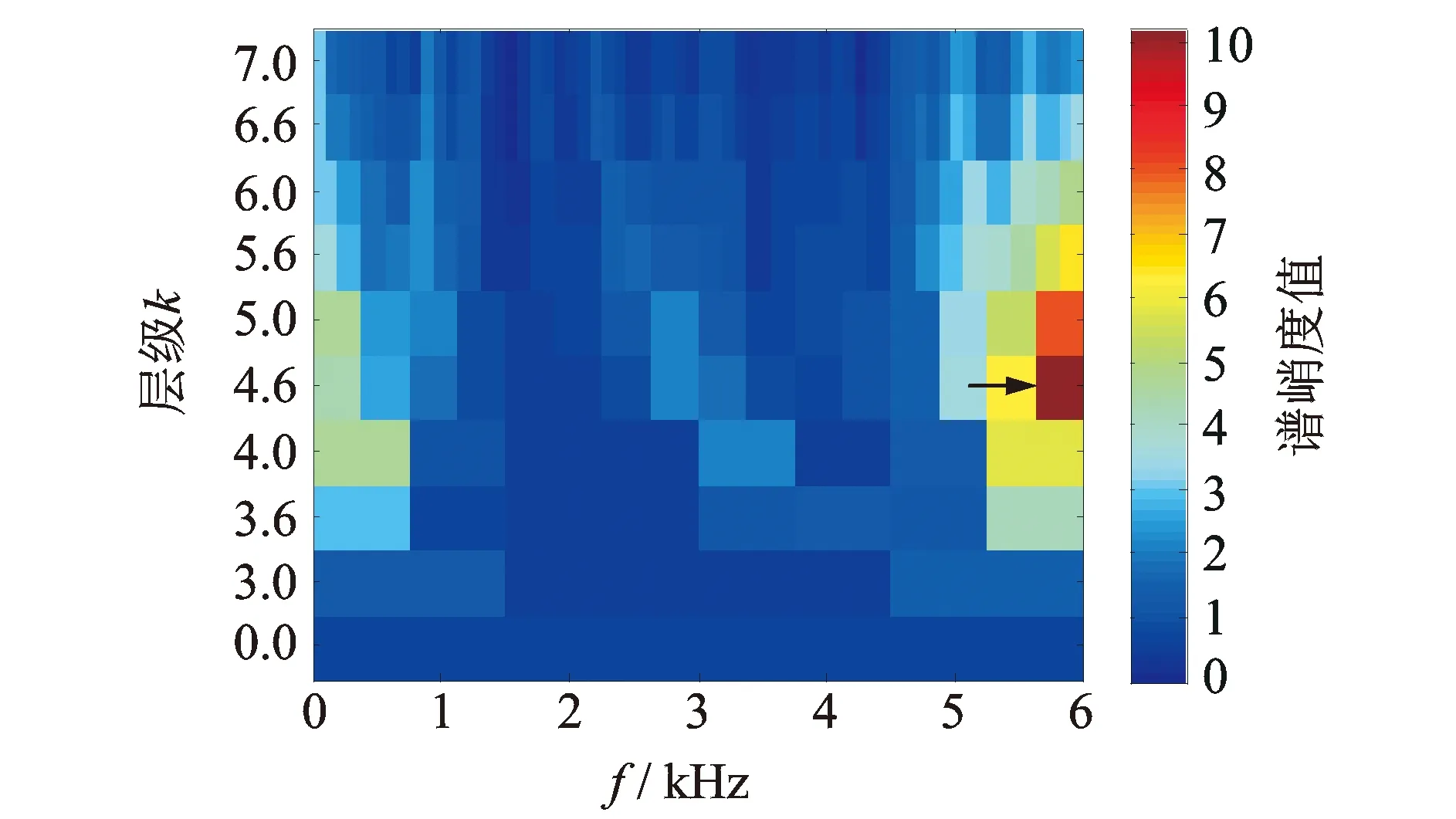
图9 滚动体故障信号的快速谱峭度图

根据滚动轴承故障诊断的特点，利用包络分析对上述两种方法所选出的敏感IMF进行处理。图10为使用谱峭度和相关系数法选取的敏感IMF(IMF1)的包络谱，对比原信号包络谱，发现IMF1与原信号的包络分析结果相类似，滚动体故障特征频率明显，亦出现了如点划线框所示的干扰项。图11为使用快速谱峭度图方法选取的敏感IMF(IMF3)的包络谱，发现滚动体故障特征频率明显，部分干扰项得到了抑制。

图10 利用谱峭度和互相关系数方法选取的敏感IMF包络谱

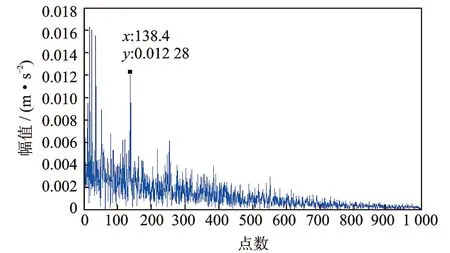
图11 利用快速谱峭度图方法选取的敏感IMF包络谱

对3组包络谱(原信号、IMF1和IMF3)做进一步分析，发现它们均能识别出故障特征频率。可以假定冲击故障特征信息分布在整个频带内[13]，而EEMD是一种从高频到低频分解的处理过程，故2个IMF和原信号中均含有故障特征信息。2个IMF的包络谱分析结果之间又有所不同，表明有的IMF相较于其他IMF可更明显地表达故障信息。该方法使用了谱峭度最大值所处的频带范围这一特征频带区间参数，将依靠人工经验的取舍单值参数问题简化为易于筛选的频带区间从属问题，克服了使用谱峭度、相关系数在内的单值特征参数可能出现的参考系数连续、不易区分而造成的敏感IMF选取困难问题，使敏感IMF选取方法更明确。

4 结 论

1) 针对如何从EEMD分解的一系列IMF中选取出敏感IMF的问题，提出了基于快速谱峭度图的敏感IMF选取方法。该方法利用谱峭度最大值所处的频带范围为特征频带区间，将依靠人工经验取舍单值参数问题简化为易于筛选的特征频带区间的从属问题，克服了单值特征参数可能出现的参考系数不易区分而造成的敏感IMF选取困难问题，使敏感IMF选取方法更易于实现。

2) 因EEMD分解能自适应的对非线性、非平稳信号进行分析处理,谱峭度方法特别适用于冲击信号的分析。快速谱峭度图方法可检测出最能体现故障信息的共振调制频带，因此，已有相关的将EEMD和谱峭度方法相结合的故障诊断方法研究。与其他研究不同的是，所提出的方法将快速谱峭度图运用至敏感IMF的选取问题上，以便对EEMD分解的多个IMF进行筛选，而非设计一套完整的故障诊断方案。

3) 除EEMD的敏感IMF选取外，该方法还可以推广至其他需要提取冲击信号特征的多分量选取方法中，如EMD和小波包分析等。

[1] Pan Minchun, Tsao W. Using appropriate IMFs for envelope analysis in multiple fault diagnosis of ball bearings [J]. International Journal of Mechanical Sciences, 2013, 69:114-124.

[2] Lei Yaguo, He Zhengjia, Zi Yanyang. Application of the EEMD method to rotor fault diagnosis of rotating machinery[J]. Mechanical Systems and Signal Processing, 2009, 23:1327-1338.

[3] 苏文胜，王奉涛，张志刚，等. EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J]. 振动与冲击，2010, 29(3):18-21.

Su Wensheng, Wang Fengtao, Zhang Zhigang, et al. Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearing[J]. Journal of Vibration and Shock, 2010, 29(3): 18-21. (in Chinese)

[4] 雷亚国. 基于改进Hilbert-Huang变换的机械故障诊断[J]. 机械工程学报，2011, 47(5): 71-77.

Lei Yaguo. Machinery fault diagnosis based on improved Hilbert-Huang transform[J]. Chinese Journal of Mechanical Engineering, 2011, 47(5): 71-77. (in Chinese)

[5] 彭畅，柏林，谢小乐. 基于EEMD、度量因子和快速谱峭度图的滚动轴承故障诊断方法[J]. 振动与冲击，2012，31(20)：143-146.

Peng Chang, Bo Lin, Xie Xiaole. Fault diagnosis method of rolling element bearing based on EEMD,measure-factor and fast kurtogram[J]. Journal of Vibration and Shock, 2012，31(20)：143-146. (in Chinese)

[6] 张志刚，石晓辉，施全，等. 基于改进EMD和谱峭度法滚动轴承故障特征提取[J]. 振动、测试与诊断，2013, 33(3)：478-482.

Zhang Zhigang, Shi Xiaohui, Shi Quan, et al. Rolling bearing element fault feature extraction based on improved EMD and spectral kurtosis[J]. Journal of Vibtation, Measurement & Diagnosis, 2013, 33(3)：478-482.(in Chinese)

[7] Wu Zhaohua, Huang N E. Ensemble empirical mode decomposition:a noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009(1):1-41.

[8] 从飞云，陈进，董广明. 基于谱峭度和AR模型的滚动轴承故障诊断[J]. 振动、测试与诊断，2012, 32(4)：538-541.

Cong Feiyun, Chen Jin, Dong Guangming. Spectral kurtosis and AR model based method for fault diagnosis of rolling bearings[J]. Journal of Vibtation, Measurement & Diagnosis, 2012, 32(4)：538-541.(in Chinese)

[9] Dwywe R F. Detection of non-Gaussian signals by frequency domain kurtosis estimation[C]∥Acoustics, Speech and Signal Processing. Boston: IEEE Inter-national Conference on ICASSP, 1983: 607-610.

[10]Antoni J. The spectral kurtosis:a useful tool for characterizing non-stationary signals[J]. Mechanical Systems and Signal Processing, 2006, 20:282-307.

[11]Antoni J. Fast computation of kurtogram for the detection of transient faults[J]. Mechanical Systems and Signal Processing, 2007, 21:108-124.

[12]Lei Yaguo, He Zhengjia, Zi Yanyang. EEMD method and WNN for fault diagnosis of locomotive roller bearings[J]. Expert Systems with Applications, 2011, 38:7334-7341.

[13]Jiang Ruihong, Liu Shulin, Tang Youfu, et al. A novel method of fault diagnosis for rolling element bearings based on the accumulated envelope spectrum of the wavelet packed[J]. Journal of Vibtation and Control,2015,21(8):1580-1593.

10.16450/j.cnki.issn.1004-6801.2015.06.027

*国家自然科学基金资助项目(51175316)；高等学校博士学科点专项科研基金资助项目(20103108110006)

2013-10-26；

2013-12-26

TH911； TH165.3

蒋超，男，1987年10月生，博士研究生。主要研究方向为机械故障诊断的信号处理方法。 E-mail：jc31@163.com