热应力对机翼结构固有频率的影响分析*

贺旭东，吴 松，张步云，陈怀海

(南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)



热应力对机翼结构固有频率的影响分析*

贺旭东，吴 松，张步云，陈怀海

(南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)

研究了热应力对飞行器机翼结构固有频率的影响。用ANSYS建立机翼结构有限元模型，计算了均匀温度场、非均匀温度场和非均匀可变温度场条件下的结构热应力分布和振动模态。根据固有振动的结构变形,分析了热应力对固有频率的影响效应。研究结果表明，热环境下机翼结构因材料属性的退化导致固有频率下降，但对于振型节线处于翼面内部的振动模态，附加热应力刚度矩阵在结构总刚度矩阵变化中起主导作用，使该阶固有频率增大。

高超声速； 热应力； 固有频率； 可变温度场

引 言

随着高超声速飞行器的发展及飞行速度的提高，人们开始认识到热效应是研究高速飞行器结构气动弹性力学的关键因素之一，在结构动力学分析与设计中必须考虑温度效应的影响。

热效应使结构材料属性下降，并在结构内部产生分布不均匀的热应力，引起飞行器结构振动特性发生改变。Heeg等[1]对两个不同材料制造的航天飞机的真实飞行状态进行了研究，结果表明，航天飞机表面真实温度从常温变化到2 700 ℃以上时，结构的固有频率剧烈变化高达30%以上。Sabour等[2]研究了旋转结构在热环境下的振动问题，指出结构固有频率受到温度场和离心刚度的共同影响。Malekzadeh等[3-5]研究了功能梯度材料结构在热环境中的自由振动问题，分析了温变、材料属性等参数对结构固有频率的影响。杨志斌等[6]采用MSC Patran软件建立了某发动机进气波纹管结构的有限元模型,进行了热应力及热模态分析。黄世勇等[7]对变厚度板进行了瞬态热环境下模态分析，结果表明受热后结构固有频率均呈下降趋势。陶海亮等[8]研究了气热固耦合场对涡轮模态参数的影响，表明气热固耦合场主要影响涡轮结构的模态固有频率,对模态振型的影响较小。王宏宏等[9]研究了加热状态下变厚度导弹翼面模型的振动特性，表明热效应引起材料弹性模量等参数的变化比热应力对固有频率的影响更大。吴振强等[10]研究了热环境对四周简支飞行器热防护系统金属加筋壁板的结构固有模态影响，结果表明，壁板结构在热环境下易发生屈曲，热模态分析中需考虑热屈曲、大位移变形等因素。

综上所述，分析热环境中热效应对结构振动特性的影响是非常必要的。目前已有一些对热环境下结构固有频率变化趋势的研究，但在复杂的加热条件下，热应力导致结构固有频率上升还是下降尚不明确，特别是对于高超声速飞行器机翼这类面临复杂温度环境的结构，需要具体问题具体分析。

笔者利用ANSYS Workbench有限元软件建立不同温度条件下的机翼结构有限元模型，计算了均匀温度场、非均匀温度场和非均匀可变温度场条件下的热应力分布和振动模态。根据固有振动的结构变形和热应力分布情况，重点分析讨论热应力对机翼结构固有振动频率的影响。

1 基本理论

模态是结构的固有特性，根据振动理论，机翼结构的模态参数可通过式(1)求解

(K-ω2M)φ=0

(1)

其中:K为结构总刚度矩阵；M为质量矩阵；φ为振型向量。

热环境条件下，结构的模态主要受到材料参数随温度的变化和热环境引起的结构内部热应力的影响。另外，对于机翼结构而言，还需考虑几何非线性等因素。当机翼结构受到热载荷后，式(1)中质量矩阵M的改变可忽略不计，而结构材料参数随温度增加而发生较大的变化。在考虑温度影响时，结构刚度矩阵[11]可表示为

(2)

其中：B为几何矩阵；D为与材料弹性模量E和泊松比μ有关的弹性矩阵。

另一方面，温度变化产生的温度梯度导致结构内部出现热应力，需要在刚度矩阵中考虑热应力的影响，结构的热应力刚度矩阵可表示为

(3)

其中：G为形函数矩阵；Γ为结构热应力矩阵。

在求解热环境下结构模态参数，需综合考虑热环境引起的材料参数变化和热应力对刚度矩阵的影响。在热环境条件下，结构的总刚度矩阵K为

K=KT+Kσ

(4)

其中：KT为结构刚度矩阵；Kσ为热应力刚度矩阵。

式(4)中，结构刚度矩阵KT与结构的物理属性有关，温度上升时材料弹性模量下降，使总刚度矩阵呈减小趋势。热应力刚度矩阵Kσ则与结构热应力形式有关，当热应力为拉应力时，Kσ为正值，结构固有频率出现上升；当热应力为压应力时，Kσ为负值，结构固有频率出现下降。由于前者与结构刚度矩阵KT对固有频率的影响趋势刚好相反，因此在热环境中，由热拉应力产生的附加热应力刚度矩阵Kσ是否在总刚度矩阵K的变化过程中占主导作用，将直接影响固有频率的变化趋势。

2 有限元分析

2.1 分析流程

对于热效应作用的机翼结构，若同时考虑热应力等影响因素，采用理论公式直接进行振动模态求解则难度非常大。笔者采用ANSYS Workbench有限元分析软件对热环境下的机翼结构振动模态进行计算，图1为结构热模态计算的流程示意图[12]。

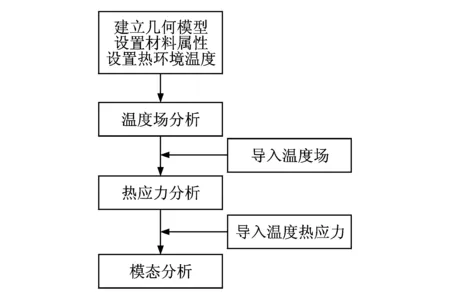
图1 结构热模态计算流程示意图

图1中温度场分析是计算流程的基础，软件根据热环境的温度设置计算得到结构温度场分布，再通过热应力分析计算结构内部的热应力分布。在进行热模态计算时，热应力分布作为载荷导入加载在结构上形成附加热应力刚度矩阵Kσ，而结构刚度矩阵KT受温度场影响发生减小退化，两者综合形成结构总刚度矩阵K，通过求解式(1)完成结构热模态计算。

为了详细分析热应力对结构固有频率的影响，笔者对机翼模型施加不同温度的热载荷，以获得不同工况下的热应力分布形式。具体计算工况如下：

1) 均匀温度场条件下热应力对结构固有频率变化的影响；

2) 非均匀温度场条件下热应力对结构固有频率变化的影响；

3) 非均匀可变温度场条件下热应力对结构固有频率变化的影响。

2.2 有限元建模

机翼结构材料为钛合金TA15，试验件如图2所示，机翼结构底端固支。机翼底端长为200 mm，上端长为130 mm，高度为150 mm，厚度为2 mm。使用ANSYS Workbench软件建立有限元模型，分析时采用体单元模拟该机翼结构。

图2 试验模型照片及有限元模型

机翼结构材料TA15的密度为4 450 kg/m3，泊松比为0.39，其他随温度T变化的材料属性，如弹性模量E、热膨胀系数α、热传导系数λ和比热容C等热特性参数值[13]如表1所示。

3 数值计算与分析

3.1 均匀温度场热应力影响分析

首先对机翼结构施加常温20℃、高温500℃和600℃的均匀温度场载荷，在不考虑热应力的情况下，分别计算3种温度条件下前6阶结构的固有频率变化趋势，如图3所示。

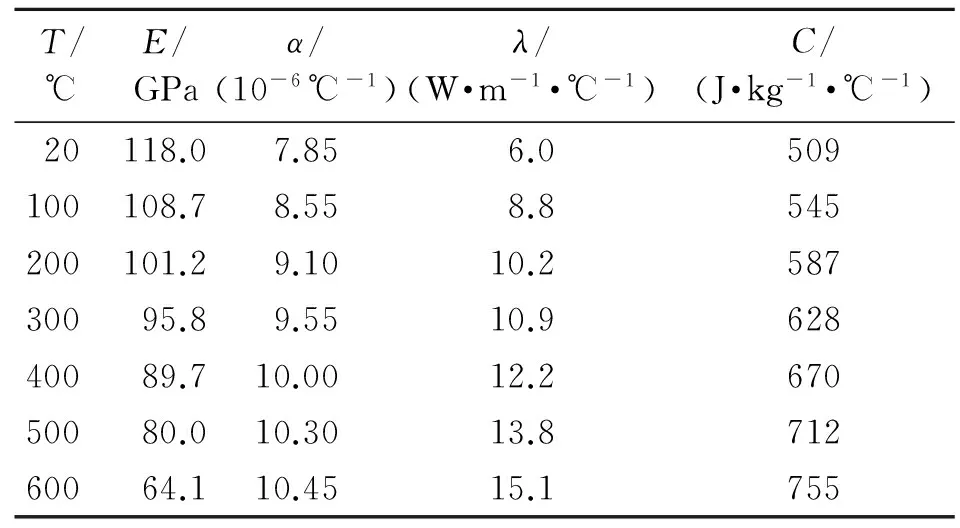
表1 TA15材料属性

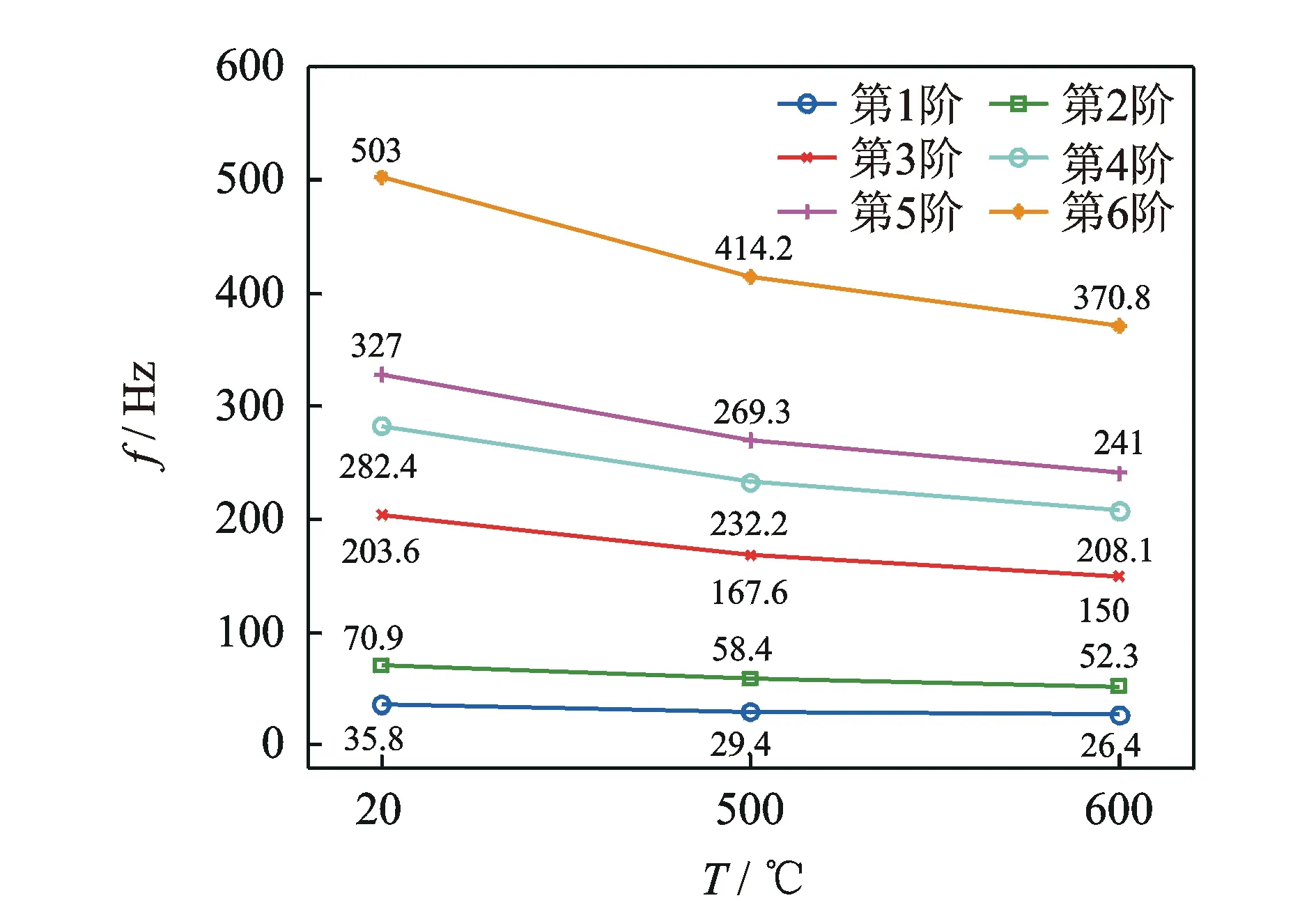
图3 前6阶固有频率变化趋势

由图3可知，随着温度的增加，每一阶固有频率呈逐步下降趋势。这是由于机翼结构的材料弹性模量随温度升高而减小，导致结构总刚度矩阵下降。在不考虑热应力的情况下，热环境将引起机翼结构的固有频率下降。

为分析热应力对结构固有频率的影响，计算机翼结构在500℃高温均匀温度场环境下的热应力分布，热应力分布云图如图4所示。由图可知，机翼结构最大热应力值位于底端固定部位，这主要是由约束所致。机翼翼面处最小热应力仅为48 Pa，且分布均匀。

图4 500℃均匀温度场热应力分布

将热应力分布作为载荷导入加载在结构上并进行热模态计算，可得到在考虑热应力的情况下的机翼结构前6阶固有频率。与图3中不考虑热应力时500℃均匀温度场固有频率数据作对比，如表2所示。

表2 均匀温度场热应力对固有频率影响对比

由表2中数据可知，在均匀温度场条件下，结构内热应力分布对固有频率几乎没有影响。这是因为均匀温度场使结构内部温度分布一致，图4热应力分布云图中显示结构内部热应力数值很小，不能产生较明显的热应力效应，因而结构的固有频率不会有太大的变化。

3.2 非均匀温度场热应力影响分析

为了分析非均匀温度场产生的热应力对结构固有频率的影响，笔者对机翼模型翼面不同部位施加不同的温度载荷，如图5所示，形成非均匀的温度场。根据结构热胀冷缩原理，温度高的部位将承受热压应力，温度低的部位将承受热拉应力，图6所示为结构在这种非均匀温度场情况下的热应力分布云图。

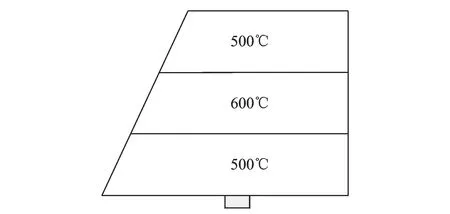
图5 非均匀温度场分布图

图6 非均匀温度场热应力分布

由图6可知，在非均匀温度场条件下，机翼结构内最大热应力值仍然处于底端固定部位，由约束所致；而翼面内的最小热应力值达44 kPa，远大于图4中均匀温度场条件下的热应力最小值。

根据图6非均匀温度场的热应力分布进行结构热模态分析，计算得到结构的前6阶固有频率，并与500℃均匀温度场条件下考虑热应力时的固有频率数据作对比，如表3所示。

表3 均匀温度场与非均匀温度场固有频率值对比

分析表3中500℃均匀温度场与非均匀温度场条件下结构的前6阶固有频率数据可知，在非均匀温度场条件下结构第2,3,4阶固有频率均高于500℃均匀温度场条件下的数值。在非均匀温度场条件下，机翼结构中间部分为600℃，其他均为500℃，由于温度对结构材料属性的影响，结构的弹性模量随温度上升而下降，使得结构刚度矩阵减小，结构固有频率也相应减小，说明在热应力对结构固有频率的变化趋势上有着不同的影响效应。

根据理论公式可知，热环境下结构总刚度矩阵由热应力刚度矩阵和结构刚度矩阵组成。在第2,3,4阶固有振动时，相比较弹性模量的下降，非均匀温度场热应力所产生的附加热应力刚度矩阵起主导作用。在这种热应力作用下，结构的固有频率出现上升现象。另外结构第1,5,6阶固有频率呈现下降趋势，表明结构在该阶固有振动时，所产生的附加热应力刚度矩阵没有起到主导作用。

3.3 非均匀可变温度场热应力影响分析

通过前面的计算可以发现，虽然在热环境中结构的材料弹性模量随温度上升而下降，但内部产生的热应力使某些阶次固有频率出现上升趋势。为了重点分析热应力对结构固有频率变化的影响关系，笔者对机翼结构模型施加如图7所示的非均匀可变温度场载荷。

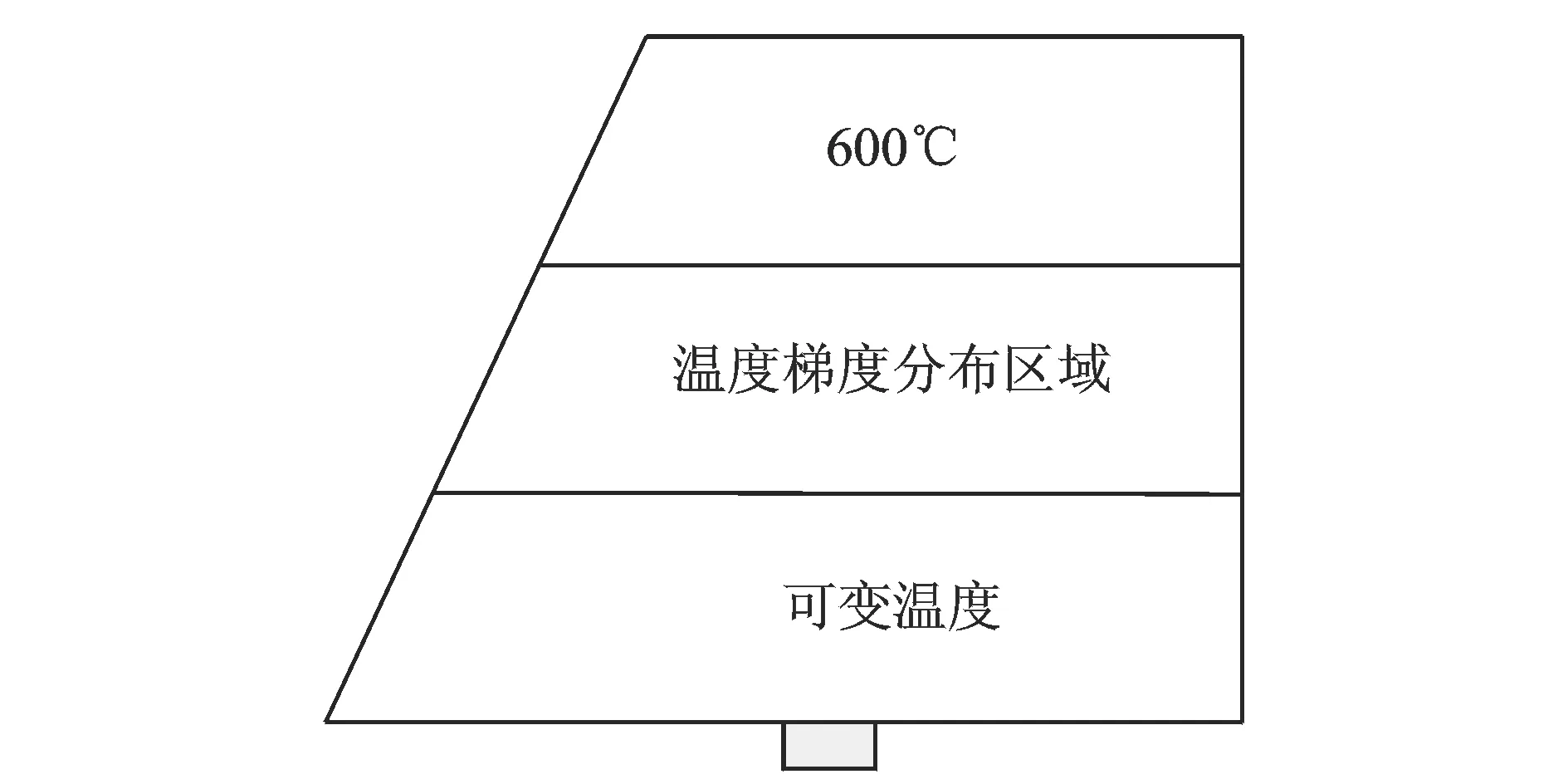
图7 非均匀可变温度场示意图

图7中结构上部分区域加载600℃温度。下部分区域加载随时间变化的温度场，其变化值分别为20,100,200,300,400,500和600℃。中间部分可根据所加载的温度形成线性分布温差梯度，由软件在计算时自动完成。同样根据热胀冷缩原理，除了600℃温度区域承受热压应力，结构的大部分区域将承受热拉应力，并且热拉应力可根据可变温度的设置而改变。

对应可变温度的每个温度值，都可以计算出结构所承受的非均匀温度分布和热应力分布状况。图8所示是可变温度为100℃条件下的结构温度场与热应力分布图。图8(a)中可见结构中间部分呈现明显的温差梯度分布；图8(b)中显示在温度场作用下结构内部呈现不均匀的热应力分布，最大热应力为154.8 MPa，最小热应力为106 kPa，整个翼面结构出现拉伸膨胀现象。

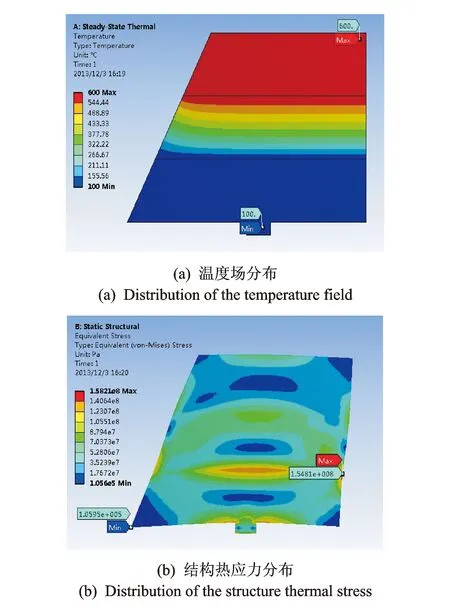
图8 100℃时非均匀温度场与结构热应力分布图

在上述非均匀可变温度场的作用下，对机翼结构进行热模态分析，计算得到每个温度条件下的结构固有模态，前6阶固有频率变化趋势如图9所示。由图9趋势曲线发现，随着可变温度的增加，机翼结构的第1阶和第5阶固有频率呈明显下降趋势，而第2,3,4和6阶固有频率则表现出先上升后下降的变化趋势。很显然，对于不同阶次的振动模态，热应力对固有频率变化趋势的影响效应是不同的。

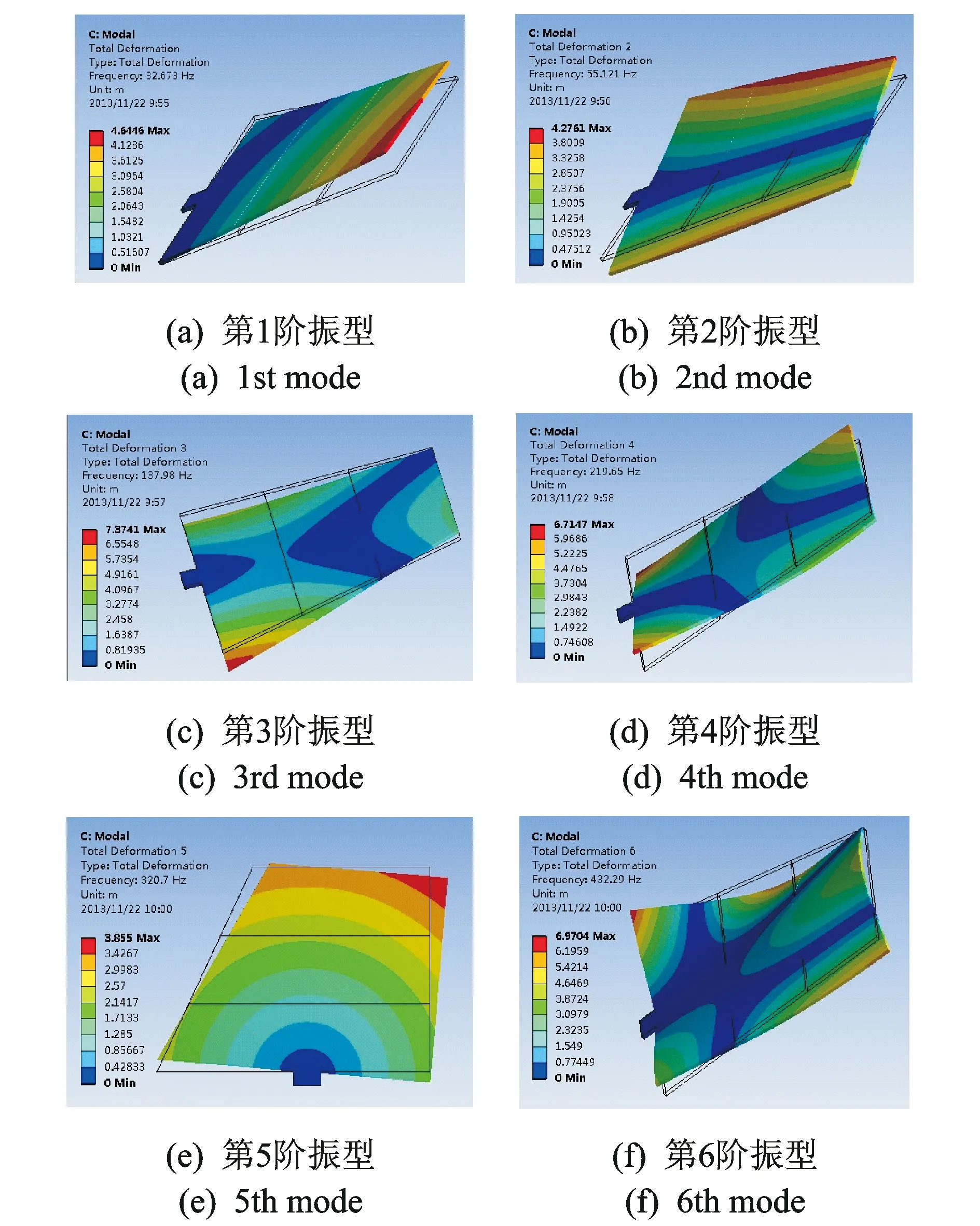
图10 非均匀可变温度场结构前6阶固有振型

经研究发现，对于本算例所采用的底端固支的机翼结构，温度场温度增加引起固有频率值发生变化，但是对每阶模态的振型影响却很小。振型表示结构作固有振动时各自由度的相对变形，因此笔者根据固有振动时结构变形和热应力分布情况，综合分析热应力对固有频率的影响。图10所示为机翼结构前6阶固有振型。

由图10可以发现，机翼结构在第1阶和第5阶固有振动时主要表现为垂直翼面方向的上下弯曲运动和沿翼面方向的左右摆动形式，振型节线靠近底端约束部位，结构没有严重的相对变形。热拉应力导致结构出现膨胀拉伸现象，但对这两种形式的固有振动没有明显影响，产生的附加热应力矩阵在总刚度矩阵变化中未占主导作用；因此，结构的刚度矩阵随温度上升而下降，使得固有频率呈下降趋势。

分析结构的第2，3，4和6阶固有振型，从图10可以看出，在这几阶固有振动中，结构出现了明显的弯曲和扭转变形现象，各阶振型的节线位于翼面内部。热拉应力导致的附加热应力刚度矩阵使固有振动的弯曲和扭转变形刚度增大，在结构总刚度矩阵变化中起了主导作用，因而使得固有频率出现上升趋势。随着可变温度的增加，结构的材料属性快速下降且温度场分布趋于均匀，虽然结构内存在热拉应力，但当温度超过一定值后，结构刚度矩阵的退化起主导作用，使得上述各阶固有频率出现先上升后下降的变化趋势。

4 结 论

1) 由于材料属性的退化，热环境中结构的固有频率往往随温度升高而下降。然而对于底端固支的机翼结构热模态分析，除了考虑由温度引起的材料属性变化，还应考虑结构热应力所产生的效应。

2) 热环境温度梯度对结构热应力分布有着重要影响，非均匀温度场条件下的结构热应力远大于均匀温度条件。对于非均匀温度场的热环境，必须考虑热应力对结构振动特性的影响。

3) 热拉应力导致的附加热应力刚度矩阵对固有频率有着重要的影响。当某阶固有振动表现出明显的弯曲或扭转运动，振型节线处于翼面内部，附加热应力刚度矩阵在结构总刚度矩阵变化中将起主导作用，使得该阶固有频率出现上升趋势。

[1] Heeg J, Zieler T A, Potozky A S, et al. Aerothermoelastic analysis of a NASP demonstrator model[C]∥AIAA/ASME/ASCE/AHS/ASC 34th Structures, Structural Dynamics and Materials Conference Technical Papers. La Jolla, CA: [s.n.], 1993:617-627.

[2] Sabour M H, Bhat R B. Vibration of rotating structures in thermal environment[J]. Advances in Vibration Engineering, 2008,7(2):167-180.

[3] Malekzadeh P, Shahpari S A, Ziaee H R. Three-dimensional free vibration of thick functionally graded annular plates in thermal environment[J]. Journal of Sound and Vibration, 2010,329(4):425-442.

[4] Malekzadeh P, Haghighi M R G, Atashi M M. Out-of-plane free vibration of functionally graded circular curved beams in thermal environment[J]. Composite Structures, 2010,92(2):541-552.

[5] Heydarpour Y, Malekzadeh P, Haghighi M R G, et al. Thermoelastic analysis of rotating laminated functionally graded cylindrical shells using layerwise differential quadrature method[J]. Acta Mechanica, 2012,223(1):81-93.

[6] 杨志斌,杨海,周东.某发动机进气管热模态分析[J].航空计算技术,2011,41(5):65-67.

Yang Zhibin， Yang Hai， Zhou Dong. Thermal mode analysis of engine inlet[J]. Aeronautical Computing Technique, 2011,41(5):65-67. (in Chinese)

[7] 黄世勇，王智勇.热环境下结构模态分析[J].导航与航天运载技术，2009(5):50-52.

Huang Shiyong, Wang Zhiyong. The structure modal analysis with thermal environment[J]. Missile and Space Vehicle, 2009(5):50-52. (in Chinese)

[8] 陶海亮,郭宝亭,谭春青.基于气热固耦合的涡轮模态分析[J].振动、测试与诊断,2012,32(6):941-944．

Tao Hailiang, Guo Baoting, Tan Chunqing. Modal analysis of turbine based on fluid-thermo-structure coupling[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(6):941-944. (in Chinese)

[9] 王宏宏,陈怀海,崔旭利,等.热效应对导弹翼面固有振动特性的影响[J].振动、测试与诊断,2010,30(3):275-279．

Wang Honghong, Chen Huaihai, Cui Xuli, et al. Thermal effect on dynamic characteristics of a missile wing[J]. Journal of Vibration, Measurement & Diagnosis, 2010,30(3):275-279. (in Chinese)

[10]吴振强,程昊,张伟,等.热环境对飞行器壁板结构动特性的影响[J].航空学报,2013,34(2):334-342.

Wu Zhenqiang, Cheng Hao, Zhang Wei, et al. Effects of thermal environment on dynamic properties of aerospace vehicle panel structures[J]. Acta Aeronautica et Astronautica Sinica, 2013,34(2):334-342. (in Chinese)

[11]王勖成．有限单元法[M]．北京：清华大学出版社，2003:441-444.

[12]凌桂龙,丁金滨.ANSYS Workbench13.0从入门到精通[M].北京：清华大学出版社，2012:257-262.

[13]中国航空材料手册编辑委员会.中国航空材料手册第四卷：钛合金、铜合金[M].2版.北京：中国标准出版社，2002：74-83.

10.16450/j.cnki.issn.1004-6801.2015.06.021

*中央高校基本科研业务费专项资金资助项目(NS2015008)

2013-12-13；

2014-02-20

O329

贺旭东，男,1978年8月生,副教授、硕士生导师。主要研究方向为机械振动和振动控制。曾发表《多点简谐振动响应控制下的频响矩阵测试》(《航空学报》2006年第27卷第5期)等论文。 E-mail:hexudong@nuaa.edu.cn