面向对象计算机控制系统中的一种时间最优滑模算法

朱 斌

（吉林省促进中小企业发展服务中心，吉林 长春 130033）

0 引 言

计算机控制系统是由计算机和自动化仪表装置与被控对象连接而成的具有各种自动化功能的技术工程系统。近年来，随着单片机、DSP（Digital Signal Processing）、FPGA（Field－Programmable Gate Array）等微处理器的迅猛发展，已经使计算机控制系统具有集成化越来越高、体积越来越小、处理速度越来越快等优点。时间最优控制［1－2］理论上是改善系统动态特性行之有效的方法，但在实际应用中由于不断以正反两个方向系统所能承受的最大控制信号施加到控制系统中，使系统的超调量变大，容易产生震颤，即系统鲁棒性变差。滑模控制根据当前状态有目的使系统结构不断改变，使系统具有快速响应、对参数变化及扰动不灵敏、鲁棒性强等优点，已成为研究热点［3－8］。

文中面向对象电机提出对电机控制系统的时间最优滑模控制。将时间最优控制的状态运动轨迹设为滑模面切换函数，设计相应的控制策略使系统状态快速趋近滑模面，并沿着滑模面快速达到空间平衡点，这样既保证了系统的快速性，又保证系统具有鲁棒性。进行了大量理论仿真研究计算机系统中全数字化时间最优滑模控制，取得很好的控制效果。

1 面向对象计算机控制系统模型的建立

控制对象为永磁同步电机，采用id＝0的控制方式可以使单位定子电流获得最大转矩。PMSM在dq坐标系下电磁转矩方程为：

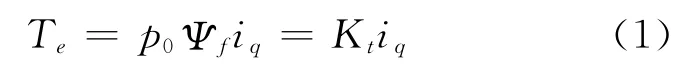
系统运动方程：

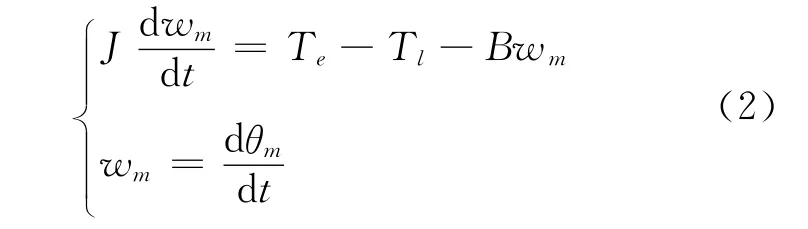
式中：Te——电磁转矩；

p0——磁极对数；

Ψf——永磁体磁链；

iq——旋转dq坐标系q轴电流分量；

id——旋转dq坐标系d轴电流分量；

Kt——电磁转矩系数；

J——转动惯量；

wm——转子机械角速度；

θm——转子机械角位置；

Tl——负载转矩；

B——摩擦系数。

在不考虑外部负载扰动Tl情况下，根据式（1）和式（2）伺服系统角位置的传递函数：

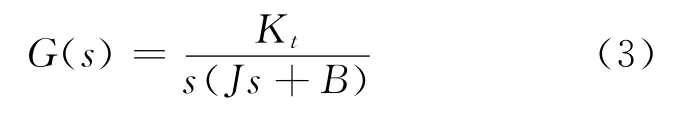
由于J≫B，故可将式（3）中摩擦系数B忽略，即式（3）可写为：

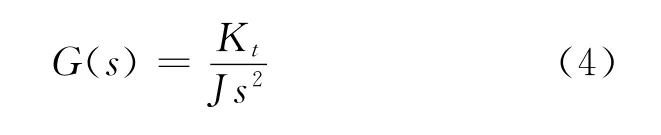
所以，此系统的模型可用双积分环节代替，即状态空间可表示为：

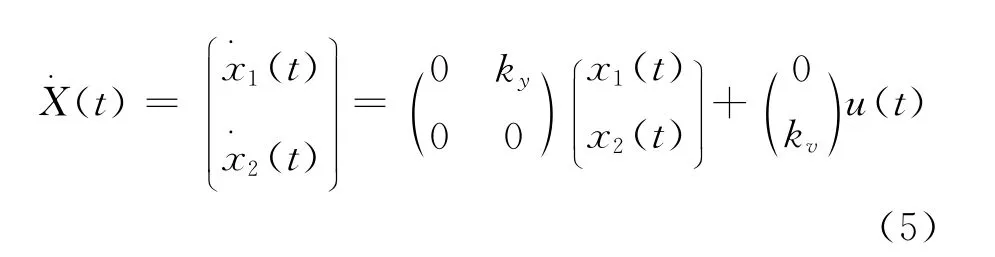
设状态变量

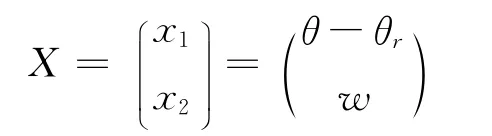
式中：θ——转子的机械角位移；

θr——给定的角位移；

w——角速度。

在计算机控制系统中，式（5）可表示为：

式中：T——采样周期。

2 时间最优控制算法

线性定常系统，其状态完全可控，状态方程

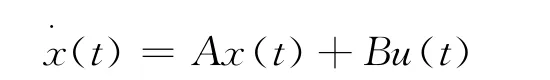
时间最优控制为使系统从任意初始状态x（0）＝x0转移到空间状态平衡点（即x（tf）＝0）的时间最短［9］。性能指标如下：

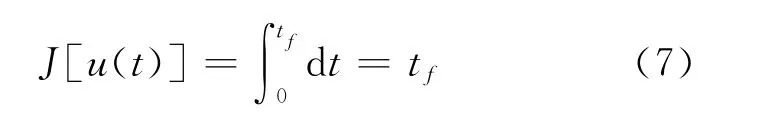
式中：tf——最终时刻；

u（t）——控制律。

式（7）取最小值的控制过程。文中

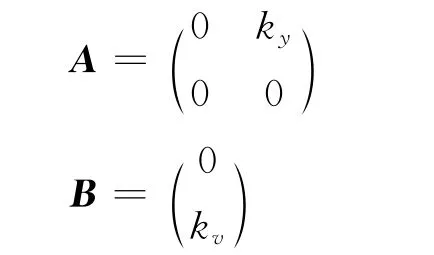
式中：A——状态转移矩阵；

B——控制矩阵。

令式（5）中u（t）＝umax，得

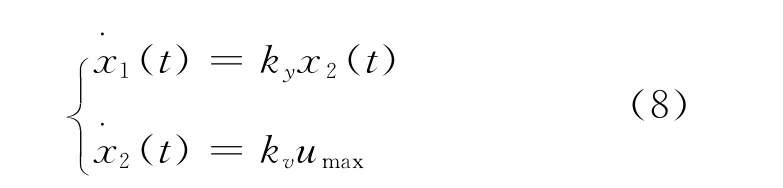
解方程（8）得

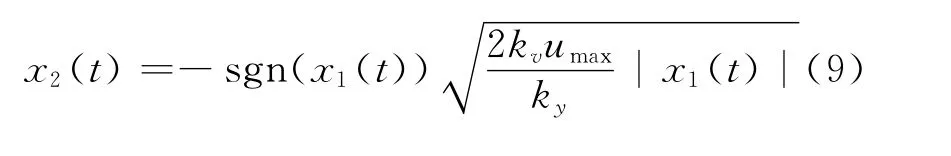
由上式得时间最优状态轨迹切换函数：

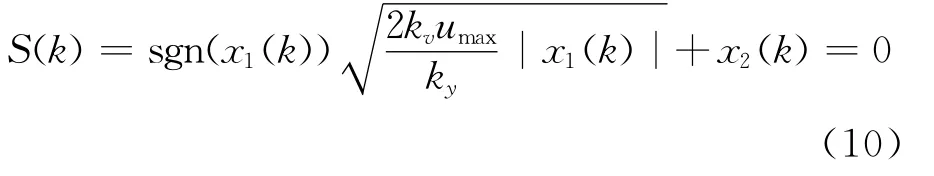
式中：sgn——符号函数。

由文献［2］知时间最优控制律为：

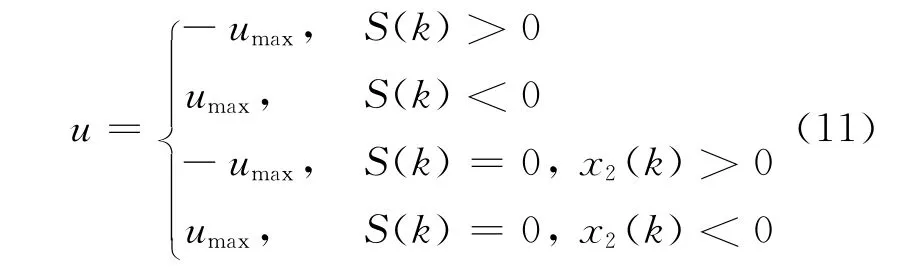
式中：umax——控制量u的最大值。

3 时间最优滑模控制算法

由文献［6］知，当系统状态变量处于滑模面时，系统对参数摄动和外部扰动具有很好的鲁棒性。因此，如果将滑模面函数取为时间最优控制轨迹构成时间最优滑模控制器。采取相应控制策略使系统任一初始状态快速平稳地趋近滑模面，并沿着滑模面运动。保证系统状态快速平稳地沿着时间最优轨线运动，避免由于时间最优控制在±umax控制量切换时引起的震颤。

滑模面切换函数为：

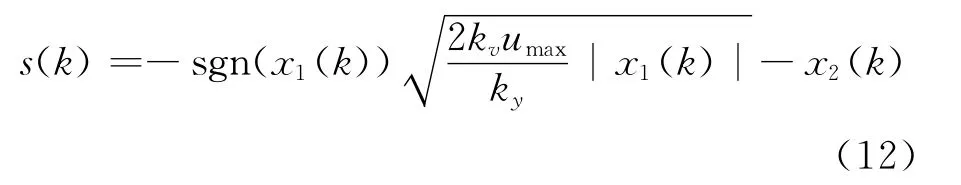
为了保证时间最优滑模控制快速趋近滑模面，文中采用指数趋近率形式如式（6），指数趋近率趋近速度从以较大值逐步减小到零，不仅缩短了趋近时间，而且还保证状态点到达滑模面时速度很小，避免系统震颤。

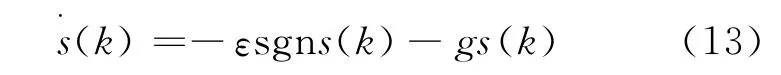
由式（6）、式（12）和式（13）得

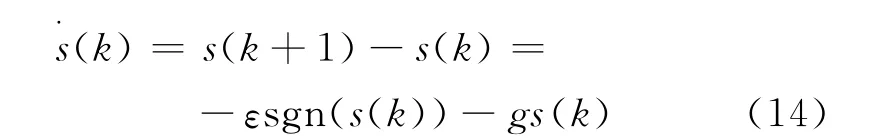
整理得出基于指数趋近率的时间最优控制器为：

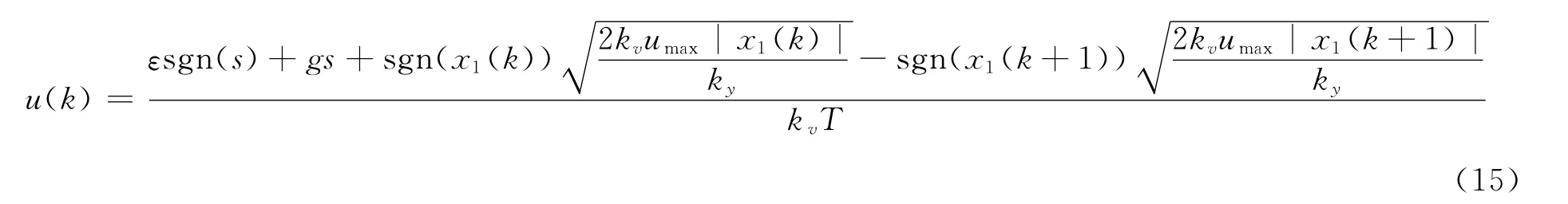
选取Lyapunov函数为

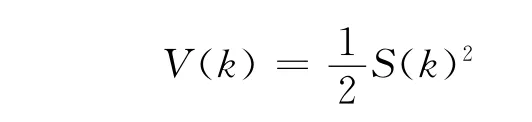
则

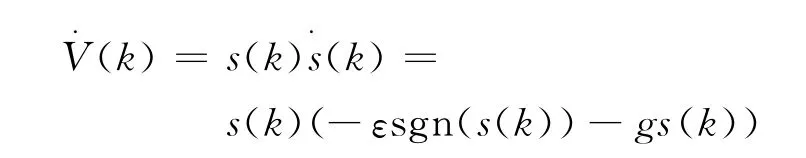
4 理论仿真研究

在Matlab中建立仿真模型并进行理论仿真研究，仿真模型如图1所示。

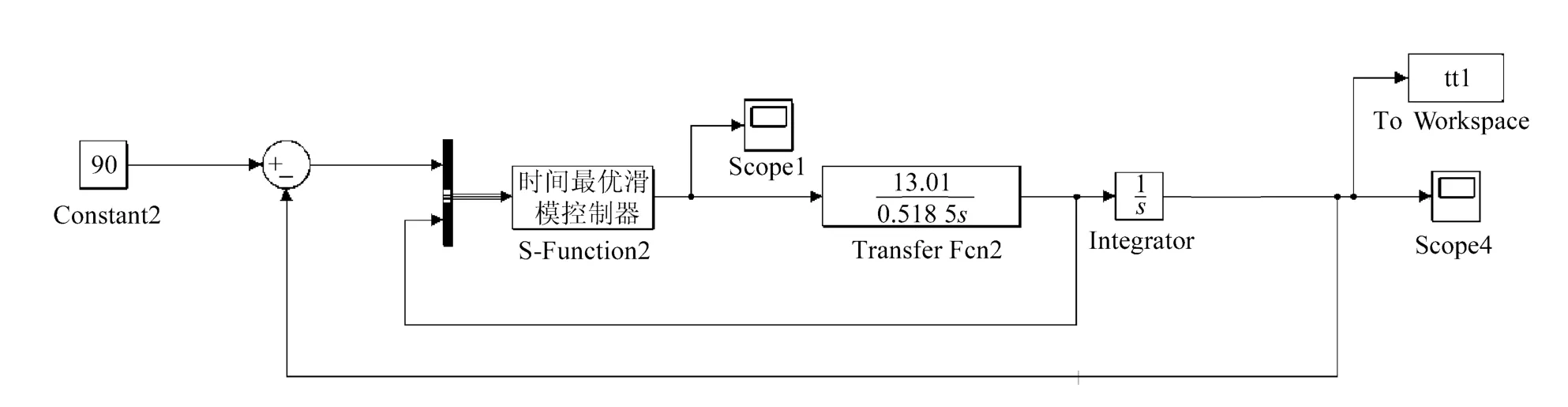
图1 时间最优滑模控制系统框图

全数字化时间最优滑模算法在S－Function中实现，仿真算法中，ky＝1，kv＝13.0／0.518 5，T＝1／800s，ε＝1.952，g＝13，umax＝15。

分别以180°、90°、60°阶跃信号为捕获目标进行仿真研究，仿真结果如图2～图4所示。

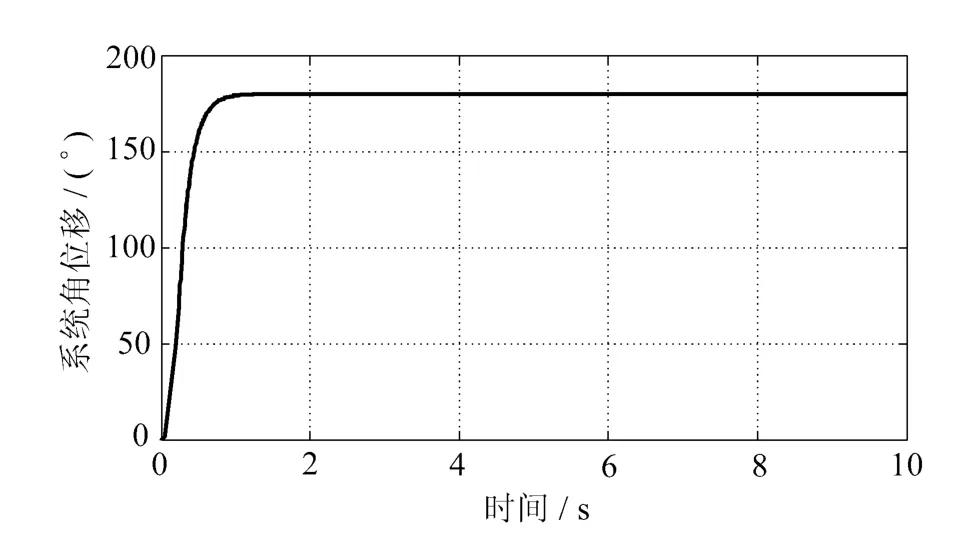
图2 180°阶跃信号仿真结果

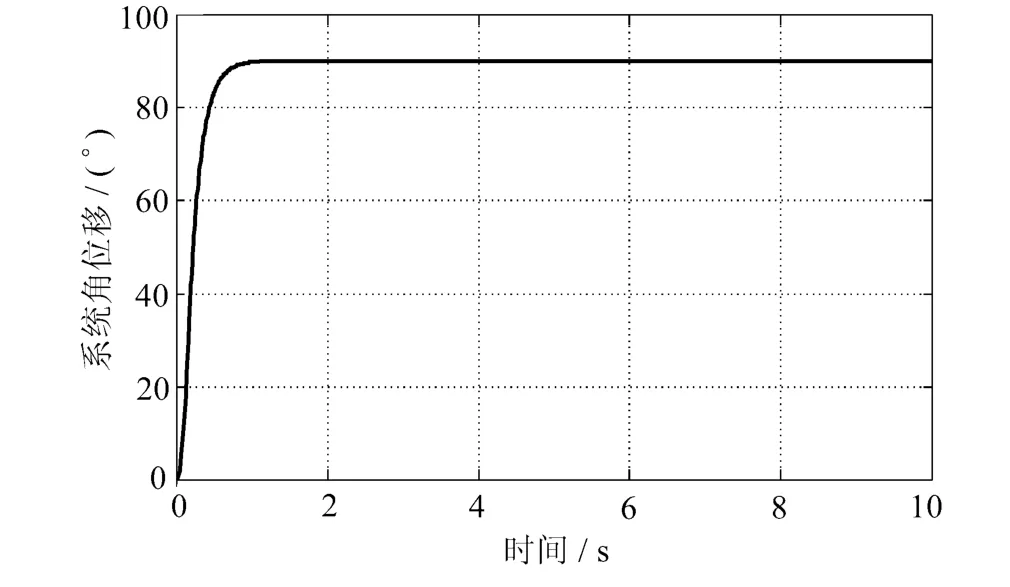
图3 90°阶跃信号仿真结果

图4 60°阶跃信号仿真结果

定量仿真结果见表1。

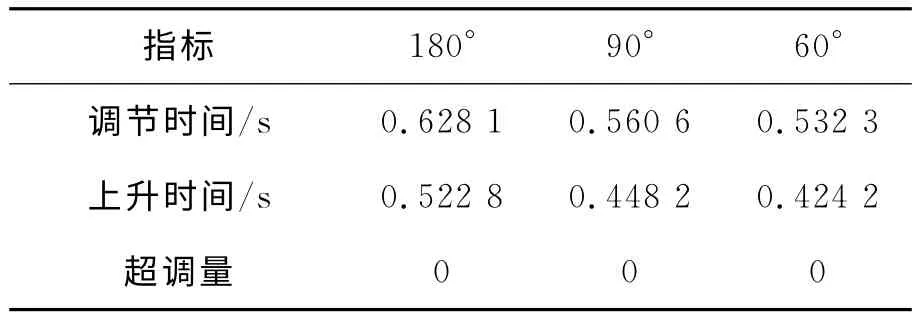
表1 时间最优滑模算法定量仿真结果

从图2～图4及表1可知，时间最优滑模控制算法上升时间及调节时间短，超调量接近0。从以上分析可知，时间最优滑模控制响应速度快，稳态误差小，定位精度高，具有重要的应用价值。

5 结 语

提出了时间最优滑模控制算法，根据计算机控制系统的特点进行时间最优滑模控制算法的全数字化研究。该算法的滑模面为时间最优控制系统状态最优运动轨迹，设计相应的趋近率。使时间最优滑模控制不仅具有时间最优控制与滑模控制的快速调节性，还有滑模控制的鲁棒性。最终以180°、90°、60°阶跃信号进行仿真研究，仿真结果为时间最优滑模控制调节时间、上升时间短，超调量为0。最终结果表明，时间最优滑模控制调节时间短、超调小、稳态值平稳、稳态误差小、鲁棒性强等优点适合应用于光电跟踪系统目标快速捕获，具有重要的研究与应用价值。

［1］ 程国扬，曾佳福.快速定位伺服系统的控制器设计［J］.电机与控制学报，2009（1）：52－56.

［2］ Zhang D Q，Guo G X.Discrete－time sliding mode proximate time optimal seek control of hard disk drives［J］.Control Theory and Applications，IEE Proceedings，2000，147（4）：440－446.

［3］ 常琳，金光，范国伟，等.基于terminal滑模控制的小卫星机动方法［J］.光 学精密工程，2015（2）：485－496.

［4］ Ji Y J，Lee C W，Chung C C，et al.A discrete－time modified sliding mode proximate time－optimal servomechanism for scanning－probe－microscope－based data storage［J］.IEEE Transactions on Magnetics，2008，44（11）：3750－3753.

［5］ Jin M，Lee J，Ahn K K.Continuous nonsingular terminal sliding－mMode control of shape memory alloy actuators using time delay estimation［J］.Mechatronics IEEE／ASME Transactions on，2015，20（2）：899－909.

［6］ 刘金琨.滑模变结构控制MATLAB仿真［M］.北京：清华大学出版社，2012.

［7］ 姚禹，杜江，姜大伟，等.伺服系统复合滑模控制仿真分析［J］.长春工业大学学报：自然科学版，2012，33（6）：611－614.

［8］ 张显伟，吴忠伟，张凤海，等.移动机器人模糊滑模轨迹跟踪控制［J］.长春工业大学学报：自然科学版，2013，34（4）：373－378.

［9］ 李凤俐.时间最优控制理论在雷达伺服系统中的应用［J］.测控技术，2008（6）：47－49.