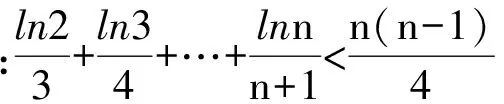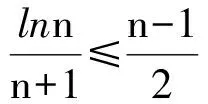巧用函数之力 追溯不等式之本质
——例谈函数构造的几个策略
●廖爱国 (云和中学 浙江云和 323600)
巧用函数之力 追溯不等式之本质
——例谈函数构造的几个策略
●廖爱国 (云和中学 浙江云和 323600)
函数可以说是整个高中数学知识体系的一个灵魂,它就像一根红线贯穿整个高中数学.函数与方程、不等式问题紧密联系,可以相互转化.函数与方程思想是新课标要求的一种重要数学思想方法,而函数构造是运用数学的基本思想方法,通过理解题意,深入分析问题的本质,构造出恰当的数学模型,利用函数的性质解决问题.函数构造的形成过程充分体现了对学生数学创造性思维能力的培养.纵观近几年各地数学高考试题,在函数压轴题中对构造新函数方法有较多考查.对此类问题,如何根据题目特点构造出恰当的函数来解决问题是解题难点,笔者结合高考试题和平时教学体会,探寻函数构造策略,以期抛砖引玉.
1 直接构造法
构造函数最常用的方法就是作差法构造函数与变量分离法构造函数,它能解决函数中很多与方程、不等式等相关问题,是函数构造中最重要的思路.
例1 设函数f(x)=x2+ax+b,g(x)=ex(cx+d).设曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
1)求a,b,c,d的值;
2)若x≥-2时,f(x)≤kg(x),求k的取值范围.
(2013年全国新课标卷数学高考理科试题)
分析 第1)小题略.第2)小题是函数中最常见的含参数恒成立问题,也是近几年数学高考和模拟卷中的常见题型,求解策略是变量分离法和作差法构造函数.
解法1 变量分离法构造函数.
由题意知,x2+4x+2≤2k·ex(x+1)对任意x≥-2恒成立,可分为3类:
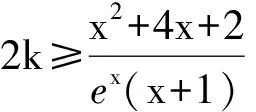
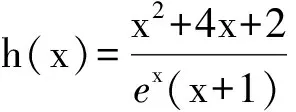
则
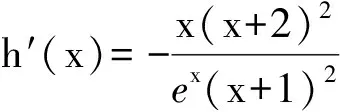
因此,当x∈(-1,0)时,h′(x)>0,h(x)单调递增;当x∈(0,+∞)时,h′(x)<0,h(x)单调递减,于是
2k≥h(x)max=h(0)=2,
得
k≥1.
②当x=-1时,左边=-1≤0=右边,f(x)≤kg(x)恒成立;
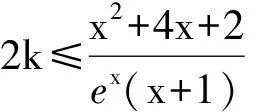
2k≤h(x)min=h(-2)=2e2,
得
k≤e2,
综上可知:1≤k≤e2.
解法2 作差法构造函数.
构造函数
h(x)=kg(x)-f(x)=2kex(x+1)-x2-4x-2,
由h(0)≥0和h(-2)≥0得1≤k≤e2.又h′(x)=2(x+2)(kex-1),令h′(x)=0,得x1=-2,x2=-lnk.
①当k∈[1,e2)时,lnk∈[0,2).当x∈[-2,-lnk)时,h′(x)<0,h(x)单调递减;当x∈(-lnk,+∞)时,h′(x)>0,h(x)单调递增,从而
kg(x)-f(x)≥h(x)min=h(-lnk)=
-lnk(lnk-2)≥0
恒成立,因此当k∈[1,e2)时,满足题意.
②当k=e2时,x∈(-2,+∞),h′(x)>0,h(x)单调递增,从而
kg(x)-f(x)≥h(x)min=h(-2)=0,
因此当k=e2时,满足题意.
综上可知:1≤k≤e2.
评析 解法1变量分离法构造函数的目的在于把含参变量的问题转化为无参变量的函数最值问题,从而避开对参变量的分类讨论,这是此类问题优先考虑的重要方法;解法2作差法构造函数思想方法常规,但若能像本题一样,先用特例缩小参变量k的取值范围,再分类讨论,则必能事半功倍,决胜考场.对这种思维的考查是近几年高考的热点之一.
2 转化构造法
在解决数学问题中常遇到直接构造求解困难的情况,此时就要注意观察式子的特点,巧妙等价转化后,再恰当构造函数,才能找到突破口.
2.1 减元与主元构造法
一杭走到核桃脸所住的病房,轻轻敲了一下门。无人应声。再敲,仍没有动静。他推门进去。核桃脸安静地躺在床上,一脸青紫,手脚微凉,已经没有鼻息。
当遇到多元参数变量问题时,需要选定参变量主次,或适当转化进行减元.
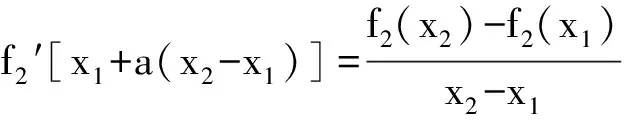
1)试求a的值;
2)记函数F(x)=b·f1(x)-lnf3(x),其中x∈(0,e],若F(x)的最小值为6,求实数b的值;

分析 本题是一道信息题,充分理解题意是求解的前提.第1)和第2)小题略,第3)小题是多元函数问题,选择不同的角度,就有不同解法,但解题的本质都是选择主元,适当变形,构造函数.
ex0(x2-x1)-(ex2-ex1)=0,
构造函数h(x)=ex(x2-x1)-(ex2-ex1),则
h′(x)=ex(x2-x1)>0,
知h(x)在R上单调递增,于是
h(x1)=ex1[(x2-x1)+1-ex2-x1].
令t=x2-x1>0,记m(t)=t+1-et,m(t)在(0,+∞)上单调递减,m(t) h(x1)<0. 同理可得h(x2)>0,又h(x)在R上连续且单调递增,从而 x1 h(t)=et-1-t(其中t>0), 则 h′(t)=et-1>0, 从而 h(t)>h(0)=0, 即 于是 得 x0>x1, 同理可得 x2>x0, 即 x1 ex0x2-ex2=ex0x1-ex1. 构造函数h(x)=ex0x-ex,则 h′(x)=ex0-ex, 知h(x)在(-∞,x0)上单调递增,在(x0,+∞)上单调递减.又因为h(x1)=h(x2),x1 x1 评析 本题第3)小题的多元变量结构整齐,适当转化,整体代换,可达到减元目的,是解题的关键.选定主元进行分析,才能从多变量中解脱出来,抓住重点,解决问题. 例3 已知函数f(x)=xlnx,g(x)=x2-6x+2. 2)求函数f(x)在区间[t,t+2](其中t>0)上的最小值. 评析 本例变形看似简单,但“变”的巧,这说明解题时,要细心观察、大胆尝试、多想一点就会有所收获. 1)求f(x)的单调区间; (2008年安徽省数学高考理科试题) 分析 仔细观察式子特点,构造函数 f(x)=ln(x-1)-(x-1)+1. 由于lnx≤x-1,得 ln(x-1)≤x-2, 取x=n2+1,则 2lnn≤n2-1, 即 评析 熟记一些常用不等关系可以方便解题,如:lnx≤x-1,x+1≤ex等. 综上可知,构造函数在解决数学函数问题中有着重要作用,其中蕴含着猜想、探究等重要思想方法,在数学教学中教师要有意识地培养学生观察分析问题的能力,既要强调通性通法的落实,也要大胆创新,不墨守成规.以上只是笔者的初浅认识,不足之处,望加以指正. [1] 蒋孝国.构造函数在解高考题中的运用[J].中学数学研究,2014(3):25-26. [2] 翟美锁.浅谈高考中的构造函数法[J].中学教研(数学),2013(9):42-43. [3] 刘再平.例谈辅助函数的构造方法[J].中等数学,2013(5):16-18.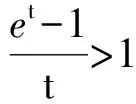
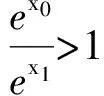
2 式子变形
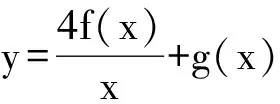
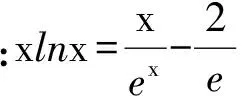

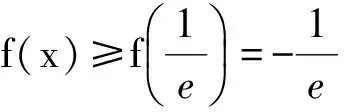
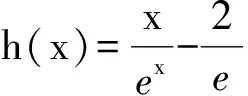
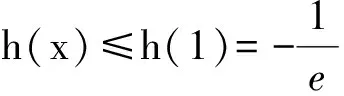
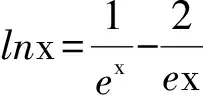
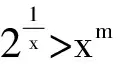
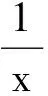
3 放缩法