应对突发事件的库存共享策略
陈敬贤,孟庆峰
(1. 南通大学商学院,江苏 南通 226019;2. 中国科学技术大学管理学院,安徽 合肥 230026;3. 江苏大学管理学院,江苏 镇江 212013)
应对突发事件的库存共享策略
陈敬贤1,2,孟庆峰3
(1. 南通大学商学院,江苏 南通 226019;2. 中国科学技术大学管理学院,安徽 合肥 230026;3. 江苏大学管理学院,江苏 镇江 212013)
以包含两个销售商的库存系统为例,构建了一个描述库存共享应对突发事件的非合作博弈模型,证明了其纳什均衡解是唯一存在的。研究结果显示库存共享策略总有可能使得销售商的期望利润得以改进。另外,比较静态分析反映了转载价格和转载成本显著影响库存共享销售商的最优订货量和最优期望利润。最后,提出了一个简单的求解模型纳什均衡解的启发式算法。
应急管理;库存共享;纳什均衡
1 引言
库存共享(Inventory Pooling)是供应链上同级企业常见合作管理库存的策略之一,也被称为横向转载(Lateral Transshipment),指的是在销售季节中,库存剩余的一方将多余的库存转运给库存不足的一方,以此在提高一方顾客满足率的同时降低另一方销售期末的剩余库存,降低库存系统总成本。自20世纪60年代被提出以来[1],学界的理论研究和企业的实践就充分显示出这一策略的显著优势,有研究表明横向转载使得零部件企业产品年库存成本降低了50%[2]。关于横向转载的研究较为丰富,更加详细的综述可参见陈敬贤[3]的归纳与总结,本文这里就不再分析。考虑到本文将利用非合作博弈理论来研究库存共享应对突发事件的绩效,因此下文将对利用博弈方法研究库存共享的研究进行简要分析。
Rudi等[4]在非合作博弈的框架下研究了存在库存共享的零售商本地决策问题(Local Decision Making),给出了两零售商纳什均衡订货策略及对应的协调转载价格。Dong Lingxiu[5]在其基础上进一步研究了非合作情形下的转载的受益主体问题,Hu Xinxin[6]结合大量数值算例和模型提出Rudi[4]提出的协调价格并不总是存在的,系统地研究了横向转载协调定价及其与相关成本参数的关系,给出了协调价格存在的条件。进一步,Hu Xinxin[7]又考虑了容量约束的限制,研究了库存共享系统中的最优库存控制决策。Hanny[8]研究了库存共享的协调机制,提出了一种基于第三方基金公司的横向转载协调机制,并给出了该机制协调多方转载的充分必要条件,证明了该机制可以协调多零售商之间的转载,并给出了该协调机制的若干优势。Anupindi[9]首先利用合作博弈的方法研究了库存共享中的转载定价问题,提出了利用剩余产品的对偶价格来定价转载产品。而Huang Xiao[10]则认为Anupindi[9]提出的对偶价格并不能协调销售商间的转载,并提出了一种新的协调转载的对偶价格。进一步,Hezarkhani[12]基于Nash谈判模型,从合作博弈的角度研究了多方转载的协调定价问题。
综合以上研究可以发现,订货决策和转载定价以及转载协调机制是利用博弈方法讨论库存共享的主要问题。也有研究考虑了其它因素对于库存共享及企业受益的影响,如Zhao Xuan[13]在价格和库存竞争性环境下,同时考虑了库存共享时的零售商定价和库存决策问题;陈敬贤[14]则基于非合作博弈方法研究了顾客退货对于具有转载行为的零售商及库存系统的影响,Lee[15]则考虑了供应链环境下下游企业转运的订货与定价决策,等等。但尚未发现有文献研究了市场需求突变下的库存共享策略及其应对需求突变的效率。事实上,作为一种同级企业间合作管理库存的方法,横向转载本身就具有一定的“应急”思想,供应链管理专家Lee[15]就研究过可修复产品库存系统的应急转载,但他们关注的是销售商缺货风险,并未考虑外部市场需求的突变风险。本文将以存在两个销售商的库存系统为例,考虑它们利用库存共享策略应对由外部突发事件引起的需求突变风险,利用非合作博弈理论研究订货策略及库存共享应对突发事件的效率问题,并在此基础上讨论用于模型纳什均衡求解的算法,期望为库存共享的理论研究及实际企业的库存管理奠定一定的理论基础。
2 模型
考虑库存系统存在两个销售商,记为销售商i(i=1,2)和销售商j(j=3-i)。销售商i面临的市场需求Xi为随机需求,其累积分布函数为F(Xi),概率密度函数为f(Xi),F(Xi)为严格递增的可微函数,f(Xi)≥0。销售商i以单位批发价格ci从外部供应商处购得产品,并以单位销售价格ri对市场销售产品。销售期初,两销售商分别对外部供应商订货,订货量记为Qi。不失一般性,假设销售期末单位产品的残值为0,销售商的单位产品缺货惩罚成本为0。由此可将销售商的期望利润Γi(Qi)表示为
Γi(Qi)=riE[min(Xi,Qi)]-ciQi。
(1)
根据Γi(Qi)关于Qi的凹性可知,Γi(Qi)取得最优的一阶条件为:
(2)
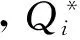
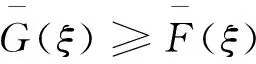
(3)
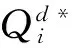
(4)
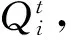
(5)
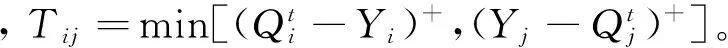
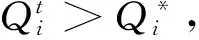
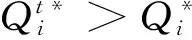
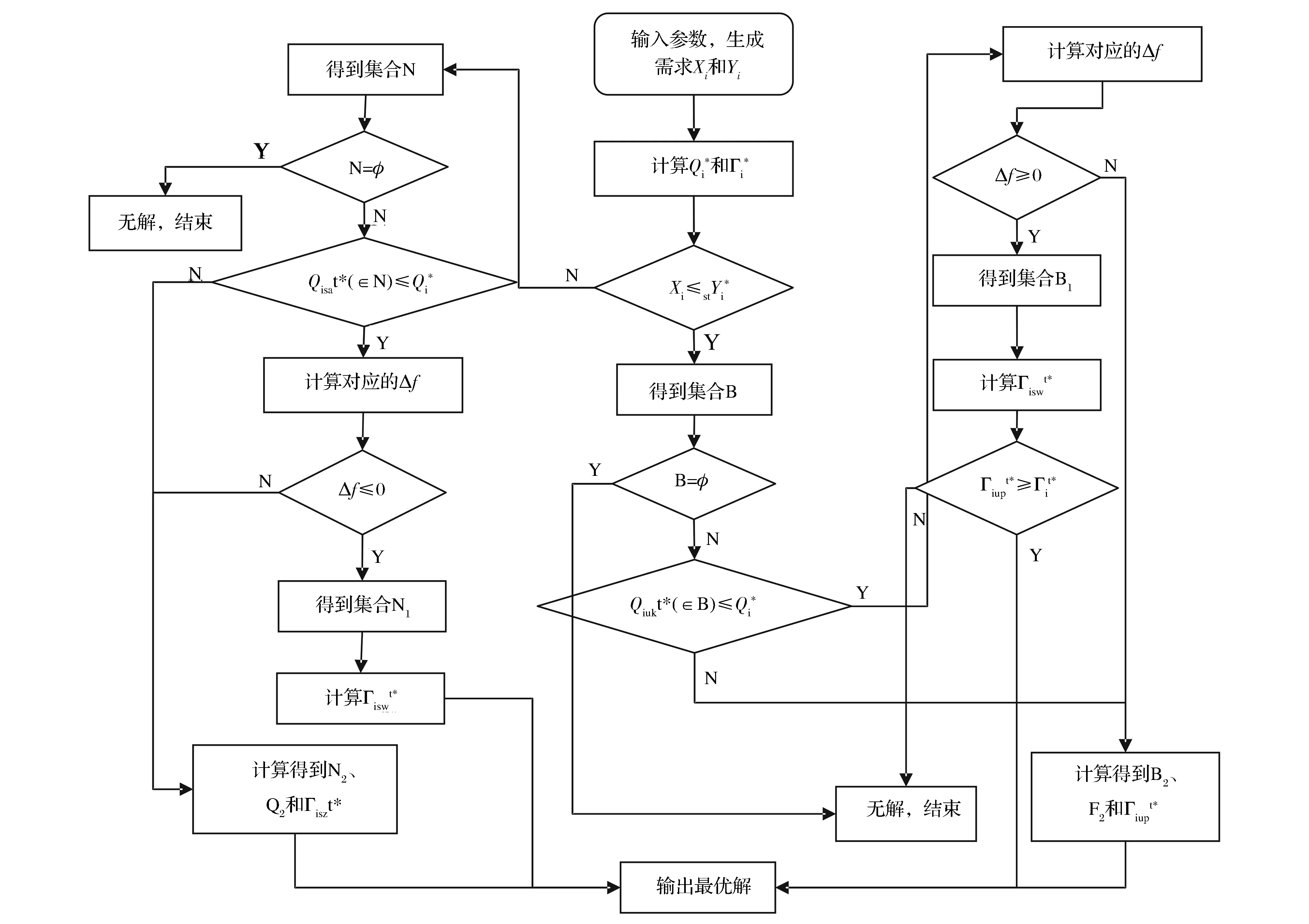
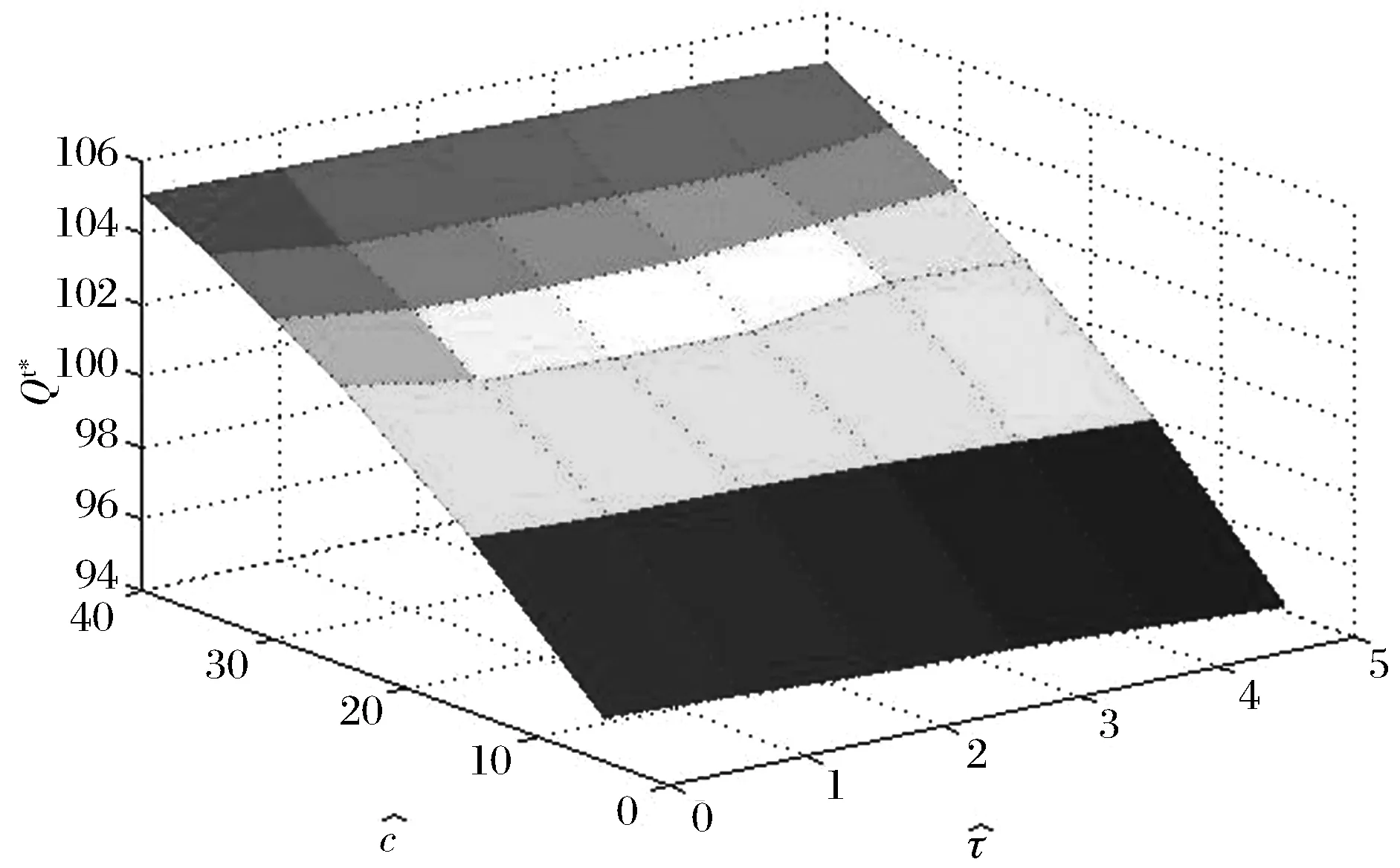
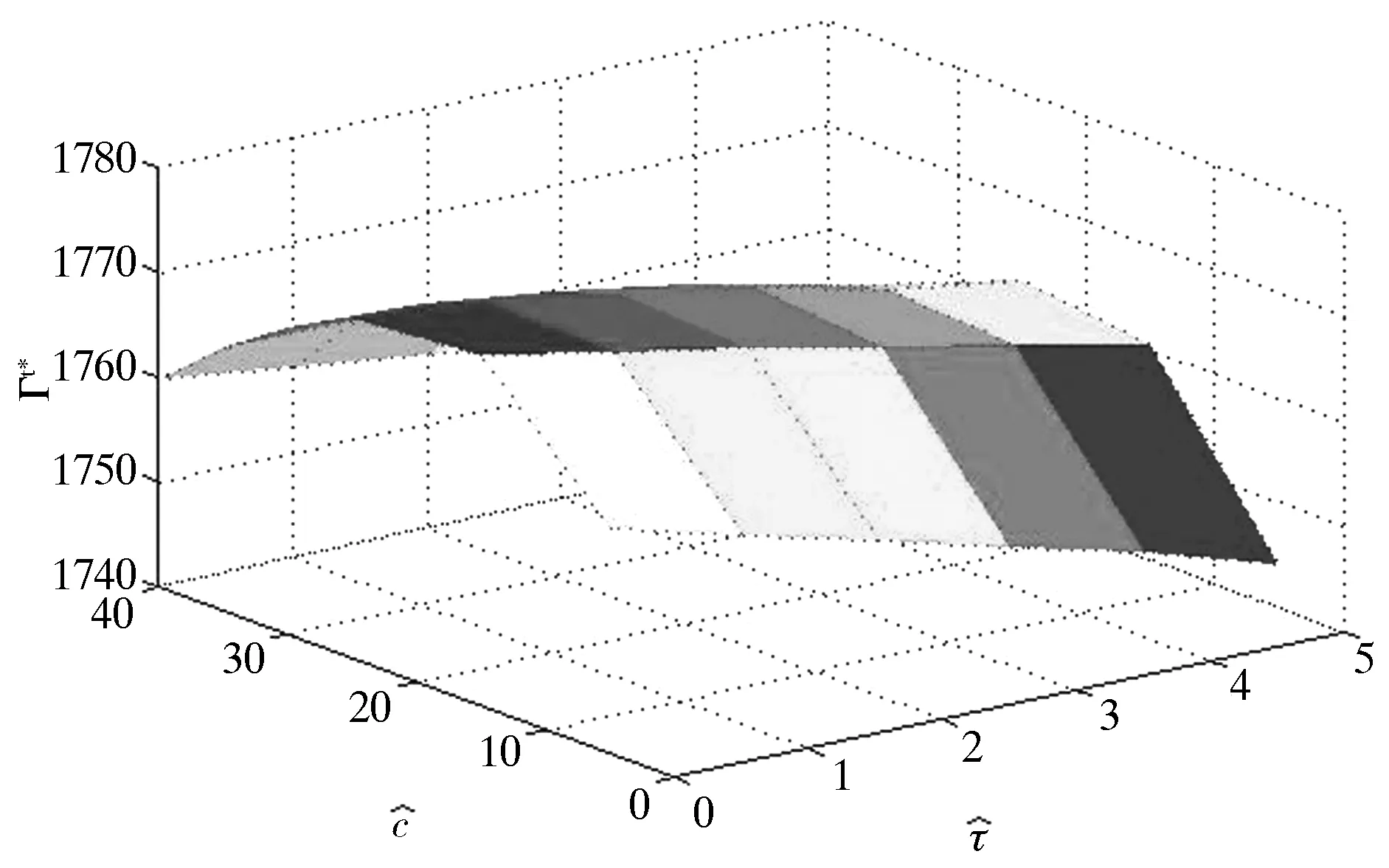
cj 以上各式中,第一个不等式保证完全利用横向转载来进行订货是不经济的,也即在供应商和销售商之间并不存在完全中转货物的“中介销售商”的存在;第二个不等式保证利用横向转载将产品从定价低的销售商处转移至定价高的销售商处从而实现高额利润是不经济的,也即横向转载并不能作为销售商之间欺诈性合谋的工具;第三个不等式说明横向转载对于转载一方是经济的,也即转载方是接受横向转载的;第四个不等式说明横向转载对于受转载一方是经济的,也即受转载方是接受横向转载的。 命题1 博弈Θ是超模的,存在唯一的纳什均衡解,由式(6)所示的最优反应函数唯一确定: (6) 其中: (7) 证明 采用文献[4]的标记方法,令 命题1表明,当需求突变发生后,若销售商采用库存共享策略,对于增大订货量或减小订货量,销售商均具有唯一的最优订货量。如果销售商不调整订货量仅实施横向转载,则只需在式(6)中令cis=ciu=0即可得到此时博弈的唯一纳什均衡解。为了进一步分析销售商在需求突变下究竟是增大订货量还是减小订货量,命题2给出了无需求突变无转载、有需求突变无转载和有需求突变有转载三种情形下的销售最优订货量间的关系。 命题3表明,当需求突变发生后,采用库存共享策略一定占优于不采用库存共享策略。但若与需求突变前的销售商最优期望利润相比,当市场突发事件使得市场需求增大时,采用库存共享策略将使得销售商的期望利润得以改进;若市场需求减小时,采用库存共享策略可能增大销售商的期望利润,也可能减小销售商的期望利润,也可能使得销售商的利润保持不变。因此,当突发事件发生后,采用库存共享策略总有可能使得销售商的利润得以改进,这也反映了库存共享策略应对突发事件的积极作用。 命题4表明,对于对称性销售商而言,随着转载价格的增大,销售商将增大订货量,而最优期望利润将表现出一种先增后减的凹性性质,存在唯一的最优转载价格,使得销售商的期望利润达到最大。利用同样的方法,可以证得推论1的结论是显然成立的。 推论1表明,随着转载成本的增大,对称性销售商将降低其最优订货量,最优期望利润也将下降。值得一提的是,命题4和推论1的结论并不受到需求突变的影响,对于无需求突变的销售商库存共享策略也是适用的。 命题1证明了博弈Θ是超模博弈,并在此基础上分析了针对销售商不同的订货调整行为,博弈Θ存在唯一的纳什均衡解。命题2则归纳了销售商在不同需求突变情景下的订货调整行为,进一步对博弈Θ的唯一纳什均衡解进行了分析。但是,销售商在观察到需求突变后,如何确定其最优订货量,如何求解博弈Θ的纳什均衡是值得思考的。因为式(6)给出的一阶条件描述了两种可能下的纳什均衡,命题2又表明了销售商最优订货量调整的不确定性,如此给博弈Θ的求解带来了困难。为此,本文设计了一种基于枚举思想的启发式算法,具体如下: 图1 算法流程 步骤11 输出最优解和最优期望利润,结束。 详细的算法流程如图1所示。 图和对最优订货量的影响 图和对最优期望利润的影响 图4 不同需求突变下的与 图5 不同需求突变下的与 图4和图5验证了命题2和命题3。由图4可知,当d≤0(市场需求减小)时,销售商将降低最优订货量,最优期望利润也将下降。当d≥0(市场需求增大)时,销售商将增大最优订货量,最优期望利润也将有所提高。图5则表明了,无论突发事件使得市场需求增大还是减小,相比较于不采用库存共享策略,采用库存共享策略都将增大销售商的最优订货量和最优期望利润。 图5 d=-1时与与的关系 图6 d=1时与与的关系 鉴于库存共享对于应对需求不确定性的诸多优势,本文利用所构建的非合作博弈模型研究了销售商如何利用库存共享来应对突发事件及其效率。研究结果表明,无论突发事件使得市场需求增大或减小,实施库存共享策略总有可能改进销售商的最优期望利润,而且明显优于无库存共享时的最优期望利润。这点结论说明了库存共享应对突发事件的积极意义。但本文并未讨论动态博弈模型及求解算法、也未讨论如何协调销售商的横向转载来应对突发事件,也未说明库存共享联盟的形成及其稳定性等问题,尚需要进一步的建模研究来分析这些重要且富有实际应用价值的课题。 [1] Gross D. Centralized inventory control in multilocation supply systems[M] // Scarf H E, Gilford D M, Shelly M W. Multistage Inventory Models and Techniques. Stanford C A: Stanford University Press, 1963. [2] Kranenburg A A. Spare parts inventory control under system availability constraints[D]. Eindhoven: Technische Universiteit Eindhoven, 2006. [3] 陈敬贤, 王国华, 梁樑. 供应链系统中零售商横向转载的随机规划模型及算法[J]. 系统工程理论与实践, 2012, 32(4): 738-745. [4] Rudi N, Kapur S, Pyke D F. A two-location inventory model with transshipment and local decision making[J]. Management Science, 2001, 47(12): 1668-1680. [5] Dong Lingxiu, Rudi N. Who benefits from transshipment? Exogenous vs. Endogenous wholesale price[J]. Management Science, 2004, 50(5): 645-657. [6] Hu Xinxin, Duenyas I, Kapuscinski R. Existence of coordinating transshipment prices in a two-location inventory model[J]. Management Science, 2007, 53(8): 1289-1302. [7] Hu Xinxin, Duenyas I, Kapuscinski R. Optimal joint inventory and transshipment control under uncertain capacity[J]. Operations Research, 2008, 56(4): 881-897. [8] Hanny E, Tzur M, Levran A. The transshipment fund mechanism: Coordinating the decentralized multilocation transshipment problem[J]. Naval Research Logistics, 2010, 57(4): 342-353. [9] Anupindi R, Bassok Y, Zemel E.A general framework for the study of decentralized distribution systems[J]. Manufacturing & Service Operations Management, 2001, 3(4): 349-368. [10] Huang Xiao, Sovsic G. Transshipment of inventories: Dual allocation vs. transshipment prices[J]. Manufacturing & Service Operation Management, 2010, 12(2): 299-318. [11] Huang Xiao, Sovsic G. Repeated newsvendor game with transshipments under dual allocations[J]. European Journal of Operational Research, 2010, 204(2): 274-284. [12] Hezarkhani B, Kubiak W. A coordinating contract for transshipment in a two-company supply chain[J]. European Journal of Operational Research, 2010, 207(1): 232-237. [13] Zhao Xuan, Atkins D. Transshipment between competing retailers[J]. IIE Transactions, 2009, 41(8): 665-676. [14] 陈敬贤, 李国昊, 施国洪. 含有顾客退货的零售商转载博弈[J]. 计算机集成制造系统, 2012, 18(10): 2303-2311. [15] Lee H L. A multi-echelon inventory model for repairable items with emergency lateral transshipments[J]. Management Science, 1987, 33(10): 1302-1316. [16] 钱宇, 陈剑. 供应链中考虑下游转运的订货和定价决策研究[J]. 中国管理科学, 2008, 16(1): 53-59. [17] Lariviere M A, Porteus E L. Selling to the newsvendor: An analysis of price——only contracts[J]. Manufacturing & Service Operations Management, 2001, 3(4): 293-305. Managing Disruption Risk with Inventory Pooling Policy CHEN Jing-xian1,2,MENG Qing-feng3 ( 1.School of Management, University of Science and Technology of China, Hefei 230026, China;2.School of Business, Nantong University, Nantong 226019, China;3. School of Business Administration, Jiangsu University, Zhenjiang 212013,China) Consider a two-retailer inventory system, a Non-cooperative game model is established to describe inventory pooling policy under disruption risk. It is proved that there exists a unique Nash equilibrium solution to the model. Model analyses show that lateral transshipments always possibly improve retailer's optimal expected profits under demand disruptions. Moreover, comparative static results reflect transshipment price and transshipment cost are two important parameters for optimal order volumes and optimal expected profits. At last, a heuristic algorithm is designed to solving the model's Nash equilibrium. disruption management; inventory pooling; Nash equilibrium 1003-207(2015)05-0065-08 10.16381/j.cnki.issn1003-207x.2015.05.009 2013-03-06; 2014-3-12 国家自然科学基金资助项目(71401082,71301062);教育部人文社会科学基金项目(14YJC630009) 陈敬贤(1982-),男(汉族),安徽人,南通大学商学院,副教授,博士研究生,研究方向:决策分析与供应链管理. F253.4 A3 纳什均衡分析
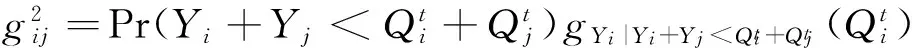
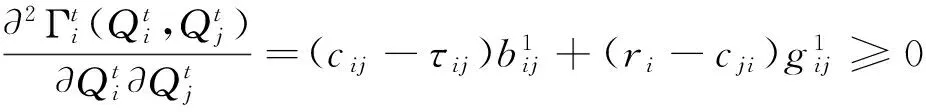
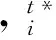

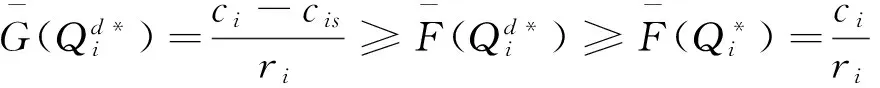
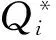

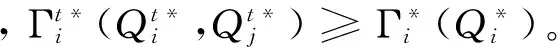
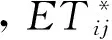
4 比较静态分析

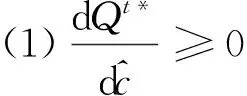
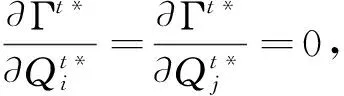
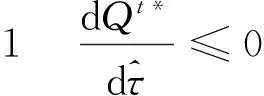
5 启发式算法

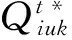
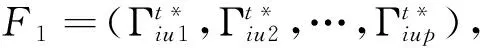
6 数值算例
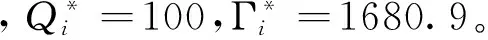

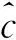
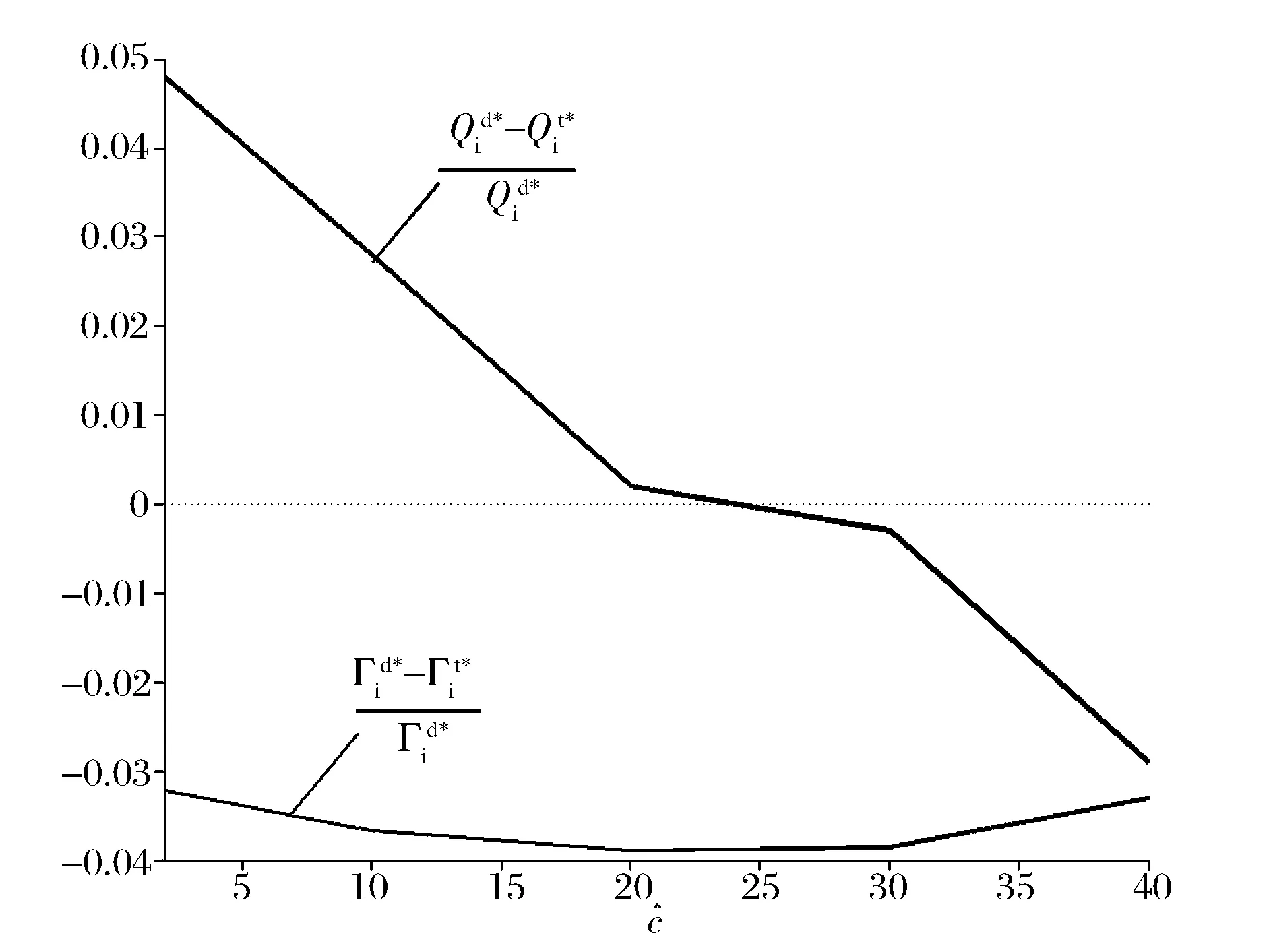
7 结语

