中国铜期货市场最优套期保值比率估计
——基于马尔科夫区制转移GARCH模型
彭红枫,陈 奕
(武汉大学经济与管理学院,湖北 武汉 430072)
中国铜期货市场最优套期保值比率估计
——基于马尔科夫区制转移GARCH模型
彭红枫,陈 奕
(武汉大学经济与管理学院,湖北 武汉 430072)
在套期保值的研究中,GARCH模型被普遍使用。但是近来许多实证研究证明了GARCH模型存在一定的缺陷,即波动率的高持续性,这影响了对于资产价格序列描述的准确性,在套期保值策略的制定时就需要考虑到波动率对状态的依赖性。因此,本文将区制转移应用到套期保值模型构建中,将MRS模型与GARCH模型相结合,建立了MRS-DCC模型,以期消除GARCH模型带来的波动率的高持续性,并用于估算铜期货市场的套期保值比率。同时,本文创新性地运用极差收益率作为标的收益率来估计套期保值比率,不仅提高了模型对资产价格日内波动的捕捉效果,而且日内价格波动的准确预测使得套期保值者规避了期货市场价格突然变化带来的强行平仓风险。本文在理论上详细解释了MRS模型与DCC-GARCH模型结合的方法,并使用中国铜期货2007年10月15日至2010年10月15日的数据进行实证分析对比,从样本内和样本外两个方面证明了马尔科夫区制转移模型以及极差收益率的引入能够提高套期保值比率估算的准确性,从而提高套期保值绩效。本文为状态依赖套期保值策略制定,以及资产价格波动风险的度量提供了参考。
套期保值比率;马尔科夫区制转移;极差收益率
1 引言
在套期保值领域的研究中,运用线性的模型来拟合现货与期货之间的相互关系,得到最优的套期保值比率,这样的方法在资产价格变动是连续、平稳的时候是可行的。但是资产价格的往往是很容易受到新信息的冲击而短期或长期的不连续变动,以铜期货市场为例,铜矿石增产或者减产的信息披露对于铜现货以及期货价格都会产生显著的影响,同样铜矿石产量的短期、长期稳定性对于铜现货以及期货价格不同时期的波动性大小也有着重要影响。因此,传统的线性模型对于这样的非线性变化资产价格序列无法准确地拟合,这时,结构性变动的引入对于提高模型拟合的精确度显然是有帮助的,运用马尔科夫区制转移构造非线性模型来对资产价格序列进行拟合,对于提高套期保值比率估算的准确性和套期保值的绩效评估是有重要意义的。
最优套期保值比率,最早是由Johnson[1]提出的。Johnson在收益方差最小化的条件下,对商品期货最佳套期保值比率进行估算。其后,Ederington[2]将上述方法应用到了金融期货市场,提出用OLS模型来估计最小方差套期保值比率。
然而OLS模型有一个重要的假定,即残差不存在异方差性,Park和Bera[3]研究发现这种假设不合理,传统的回归方法不适合最小方差套期保值比率的估计。Engle[4]提出了自回归条件异方差(ARCH)模型,通过条件异方差的形式解决了传统模型中残差存在的异方差性问题。在此基础上,随后发展到了广义自回归条件异方差模型(GARCH),这些模型通过对残差序列的进一步分析来提高模型的拟合精度。
基于条件异方差模型(GARCH),许多研究者建立了更多的计量模型进行套期保值的研究。Bollerslev[5]利用CCC-GARCH模型对短期名义汇率进行研究,随后很多研究者将此模型引入到套期保值的研究中,他们发现动态的套期保值能够获得比静态的套期保值更好的绩效。Tse和Tsui[6]进一步指出用动态的相关系数代替CCC-GARCH模型中的固定相关系数,赋予现货与期货价格序列的相关系数以时变的属性,不仅更符合经济规律,而且能够更准确地描绘资产序列的波动,这就是DCC-GARCH模型。此后该模型也被广泛应用到套期保值的研究中,并且被证明能够估算出比CCC-GARCH更准确的套期保值比率,获得更好的套期保值绩效。
随着GARCH模型的不断发展,其模型设定中的不足也逐渐被研究者所发现。GARCH模型通过引入条件方差来解释波动率的异方差性,但是这同时带来了新的问题:可能会使得方差受前期波动率的影响被过分的夸大。在GARCH模型中,若干年之前的一个较大的波动率变化,对现在的波动率仍会有比较大的影响,但是这与现实不相符。现实中更多的情况是,相隔时间较长的历史波动率对当期波动率的影响应该是微乎其微的。因此,当资产价格的历史走势中存在较为明显的大波动率周期与小波动率周期时,GARCH模型就难以准确的刻画这种特征。Lamoureux和Lastrapes[7]指出当波动率存在这样的结构性变化或者区制转移时,GARCH模型中隐含的波动率的高持续性可能是虚假的。
Fong和See[8]也发现GARCH模型倾向于对条件波动率注入一个较高水平的持续性,这意味着很久以前发生的冲击对现在仍有不可忽视的影响。实证研究表明明了对于许多资产而言,GARCH模型中的设定存在一定的偏误。
据此,Alizadeh和Nomikos[9]将MRS(MarkovRegimeSwitchingModel)模型应用于套期保值比率的估算中,并将MRS与OLS、GARCH、ECM的套期保值效果进行了比较,结果发现FTSE100指数期货市场上,样本内和样本外MRS的套期保值效果均优于其他模型,在S&P500合约上,样本内MRS套期保值效果优于其他模型。
此后,Lee和Yoder[10-11]分别将MRS模型与TVC-GARCH、BEKK-GARCH模型相结合,并进行了实证检验,发现混合模型的套期保值效果均优于单一模型的效果,证明区制转移模型的引入能够较为明显的提高套期保值比率估算的准确性与套期保值效果。
国外众多学者也从理论和实证方面证实了将MRS模型与传统的套期保值模型结合,对于存在结构性变动的情况下的资产价格非线性走势的拟合效果会更好,能够提高套期保值比率估计的准确性,从而提高套期保值效果。
国内学者也对中国期货市场的许多品种进行了套期保值方面的研究。
付胜华和檀向球[12]通过OLS简单线性回归和GARCH这两类模型来确定最小方差套期保值比率,并通过对十大基金重仓股套期保值的实证研究证明了投资组合套期保值方法能够明显的减小组合收益的波动性,降低风险。利用OLS、VAR、VECM/CC-GARCH和SSPACE五个模型,付剑茹,张宗成[13]对铜期货的套期保值比率进行估计,并比较了各模型避险绩效。发现利用卡尔曼滤波估计的状态空间模型能够得到较好的套期保值效果。
根据中国期货市场的现状,彭红枫,叶永刚[14]改进了KronerandSultan[15]的ECM-GARCH模型,提出了修正的ECM-GARCH模型,并通过对铜期货市场的实证研究证明了修正的ECM-GARCH模型能够获得更高的套期保值绩效。王辉、孙志凌和谢幽篁[16]考虑基差以及市场消息带来的非对称影响,将ADCC-GARCH模型改进为DADCC-GARCH模型,并对白糖、大豆、棉花和菜油四种期货进行了实证分析,证明了考虑基差和非对称性能够提高套期保值绩效。
国内研究主要集中于经典套期保值模型在中国期货市场的应用,由于中国期货市场建立时间较短,期货现货价格之间的基差风险较大,因此直接引用国外成熟的套期保值方法或许不符合中国期货市场的现实状况,需要对国外研究成果在中国期货市场的适用性进行验证。
而对于MRS模型,国内学者对其的应用更多地集中在经济周期的研究以及利率、汇率市场中,赵鹏曾和剑云[17]运用马尔科夫区制转移模型对股市周期性泡沫的存在性进行了实证研究,朱孟楠、刘林和倪玉娟[18]运用马尔科夫区制转移VAR模型汇率与房地产价格之间的非线性关系。但是,目前为止还没有国内的学者将马尔科夫区制转移模型与GARCH模型相结合进行套期保值研究,这方面的研究明显滞后于国外。
同时,国外对于套期保值方面的研究并不局限于套期保值模型的创新,也有一些学者开始对标的收益率的选取方面进行研究,目前套期保值比率估计中普遍采用的是日间收益率,即后一日的收盘价与前一日收盘价之差除以前一日收盘价。
但是随着研究的进一步深入,很多学者指出这种日间收益率的衡量方法有失偏颇,Parkinson[19]提出用极值法(TheExtremeValueMethod)来计算资产收益率,她们发现这一方法计算出的资产收益率在对资产价格变动特征的刻画方面明显优于传统的方法。
Anderson和Bollerslev[20]提出了实现波动率(RealizedVolatility)的概念,他们发现使用资产的高频日内收益率比使用日间收益率能够更好地刻画真实波动率,但是Mapa和Jones[21]指出当资产交易不活跃的时候,这种收益率并不适用,他们提出用极差(Range),即当日最高收益率与最低收益率之差来计算收益率,并通过实证证明使用极差收益率能够比传统方法和实现波动率获得更优的波动率拟合结果。
极差收益率对资产价格波动率的刻画比日间收益率更加准确,在实行保证金制度的期货市场中能更好地度量日内头寸的风险,及时反映保证金账户的需求。在以往的套期保值研究中,很少有研究考虑到保证金制度,但是,事实上使用日间收益率的套期保值策略为投资者确定了套期保值比率,投资者再根据这一比率建仓,如果日内价格波动过大,有可能会造成期货账户的巨额亏损,此时,追加保证金的要求会即刻反馈给交易者,若交易者不能按时追加保证金,有可能被强行平仓,导致套期保值策略失败。而使用极差收益率构建的模型能够更好地拟合和预测未来日内价格的波动,从理论上避免了由于日内价格变化过大而造成的强平。使用极差收益率来代替传统套期保值模型中的日间收益率,不仅能够更好地刻画资产价格的波动特征,而且更加契合市场制度,方便投资者对于仓位的及时调整。
目前鲜有学者尝试将区制转移模型与GARCH模型结合并将极差收益率应用于套期保值领域的研究,因此本文尝试将区制转移模型与传统GARCH模型相结合,同时使用极差收益率代替传统日间收益率,从理论与实证两方面验证这样的方法对中国期货市场套期保值绩效提高的帮助。
2 模型
2.1 极差收益率
不同于传统的模型构建方式,本文采用引言中提到的期货价格与现货价格的极差收益率,而不是日间收益率来计算套期保值比率。
当日价格收盘价高于开盘价,即当日价格上涨时:
当日价格收盘价低于开盘价,即当日价格下跌时:
Sτ、Fτ分别代表在第t个交易日内现货与期货的价格。
2.2 最优套期保值比率估计模型
2.2.1 常用的套期保值模型
传统的回归模型通过最小二乘法对期货与现货的套期保值比率进行估计,Ederington[2]运用OLS估计方法计算了最小方差套期保值比率:
ΔSt=c+h*ΔFt+εt
(1)
最小方差套期保值比率为:
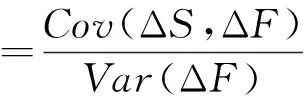
(2)
在本文中,应用极差收益率来代替现货与期货价格的变动值,估计的方程式(1)变为:
Rs,t=c+h*Rf,t+εt
(3)
最小方差套期保值比率为:
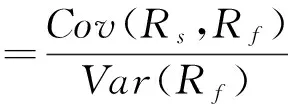
(4)
不过,随着计量方法的进步,许多实证研究证明时变的套期保值策略比静态的套期保值策略套期保值绩效更好,其中CCC-GARCH模型由于计算的简便性而被广泛应用于计算时变套期保值比率,在本文中用极差来代替资产的日收益率以期获得更好的套期保值效果。
Rs,t、Rf,t分别代表现货与期货的极差收益率。
Rs,t=μs+es,t
(5)
Rf,t=μf+ef,t
(6)
其中:
(7)
μs、μf代表了现货和期货的平均极差收益率,es,t、ef,t为残差项,ψt-1为在t-1时刻的信息集,BN为二元正态分布,Ht为一个2×2的时变正定条件协方差矩阵。
(8)
通过最大化极大似然函数法,得到时变的套期保值比率:
(9)
虽然相关系数为常数的假定能够很容易地计算套期保值比率,但是这样的假定对于一些经济数据过于苛刻了,因此Tse和Tsui[6]将常相关系数的CCC-GARCH模型拓展到了动态相关系数的DCC-GARCH模型。通过将原本假设为常数的相关系数转变为随时间变化的相关系数,因此Ht变为:
(10)
其中ρt为t时刻现货与期货极差收益率的时变条件相关系数
同样,对数似然函数最大化可以得到DCC-GARCH的动态套期保值比率。
2.2.2 区制转移MRS-DCC模型
我们首先假定存在状态变量ξt={1, 2},并且服从一阶两状态马尔科夫过程。Lee和Yodar[7-8]假定状态转移概率服从逻辑分布:
(11)
(12)
其中p0、q0是不受约束的常数,可由后续的极大似然估计得到。
现货和期货收益率变动过程也与状态变量ξt相关:
Rs,t=μs,ξt+es,t,ξt
(13)
Rf,t=μf,ξt+ef,t,ξt
(14)
其残差项服从一个与状态相关的二元正态分布:
(15)
其中Ht,ξt是状态依赖的时变2×2正定条件协方差矩阵:
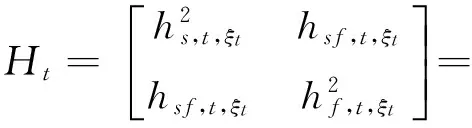
(16)
(17)
(18)
ρt,ξt=(1-θ1,ξt-θ2,ξt)ρ+θ1,ξtρt-1,ξt+θ2,ξtφt-1
(19)
所有参数均为状态依赖参数。
当将模型从DCC-GARCH拓展到MRS-DCC时,由状态变量的马尔科夫性质带来的方程的递归性,使得方程中的条件方差和条件协方差存在路径依赖的问题,为了解决这一问题,Gray[22]通过以下方程将条件残差项与条件方差重新组合:
(20)
ei,t=Ri,t-E[Ri,t|ψt-1]=Ri,t-[p1,tμi,1+(1-p1,t)μi,2]
(21)
其中i={s,f},p1,t为t时刻处于状态1的概率,定义如下:
(22)
其中:
(23)
Yt=[Rs,tRf,t]是2×1向量,包含了t时刻的现货与期货的极差收益率。
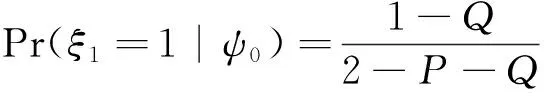
Lee和Yoder[10-11]将Gray的方法拓展到了协方差,从而解决了协方差存在的路径依赖问题。
hsf,t=Cov(Rs,t,Rf,t|ψt-1)=E[Rs,tRf,t|ψt-1]-E[Rs,t|ψt-1]E[Rf,t|ψt-1]
(24)
E[Rs,t|ψt-1]=p1,tμs,1+(1-p1,t)μs,2
(25)
E[Rf,t|ψt-1]=p1,tμf,1+(1-p1,t)μf,2
(26)
E[Rs,tRf,t|ψt-1]=E[(μs,ξt+es,t,ξt)(μf,ξt+ef,t,ξt)|ψt-1]=p1,t(μs,1μf,1+hsf,t,1)+(1-p1,t)(μs,2μf,2+hsf,t,2)
(27)
由于:
ρt=hsf,t/(hs,thf,t)
ρt,1=hsf,t,1/(hs,t,1hf,t,1)
ρt,2=hsf,t,2/(hs,t,2hf,t,2)
因此条件相关系数的方程表达式为:
(28)
通过取每个时刻的条件期望,使得ρt,1与ρt,2内含到了ρt中,当前的条件相关系数只与当前区制有关,与过去无关。
这样,MRS-DCC中所有未知参数为:
(29)
所有参数均可由最大化以下极大似然函数得到:
(30)
2.3 套保绩效衡量模型
套期保值绩效的考量主要分为两种,一种是由Ederington[2]提出的以投资组合方差的减少量为判断标准的MV法;另一种是在动态套期保值比率出现后,对于动态套期保值带来的方差的减少和交易成本的提高之间权衡,引入了效用函数,对套期保值者在这两种情形下获得的效用赋予相应的权重,通过比较不同模型带来效用值,选出效用最高的模型作为最优模型。
虽然基于效用的套期保值绩效评估在理论上更能够反映出不同套期保值模型的优劣,但是由于效用函数的确定具有很强的主观性,无法充分反映不同模型的真实优劣之别,因此本文中还是使用MV法来比较不同模型的套期保值绩效。
根据以下函数来计算各个模型中的方差减少量:
(31)
3 实证分析
根据理论模型的描述,本文运用中国期货市场上的期货品种进行实证分析,通过上述模型估算各自的套期保值比率,并比较各个模型的套期保值绩效。
3.1 数据描述
实证分析中选择的标的资产为中国的铜期货。其中,现货数据期限为2007年10月15日至2010年10月15日,共732个观察值;期货数据为SHFE市场上的铜期货合约,由于期货合约的期限性,为了获得连续的期货价格时间序列,将期货合约进行展期,对应当月的现货价格序列,取两个月后到期的期货铜价格作为期货价格序列,使用两个月后到期期货铜的原因是临近交割月的期货合约交易更为活跃,更加准确地反映期货铜价格,而交割月的价格波动不稳定,因此选择交割月前两个月的期货数据。期货数据从2007年10月15日至2010年10月15日,共732个观察值。为了进行样本内和样本外的实证检验,我们将样本区间分为了两个时期,前702个数据作为样本内数据,后30个数据作为样本外数据。
现货数据来自Wind资讯,期货数据来自国泰安数据库。
本文使用的标的收益率为极差收益率,图1显示的是铜现货序列与期货序列收益率的直观图。

图1 铜现货期货收益率
表1 现货期货序列描述性统计

现货序列期货序列平均值-0.0004818268-0.0008919395方差0.00050747910.0004897802
从上述图1和表1的描述性统计中可以看到,铜现货序列与期货序列的均值存在较大的差异,这说明了传统模型中1∶1的套期保值比率不能在现实的现货期货市场上达到完全规避风险的目的,同时观察到两者的波动率很相近,这表明能够通过期货头寸的调整达到套期保值目的,使得套期保值比率的估算有意义。
3.2 实证结果
3.2.1ARCH效应检验
对均值方程进行拟合,并对其中的残差进行ARCH效应检验。

表2 ARCH效应检验
由表中的F值与p值可以发现,现货与期货的均值方程残差均存在ARCH效应,可以建立GARCH模型。
3.2.2 区制转移效应检验
对DCC-GARCH模型中估算出的现货与期货的条件异方差序列进行分析。
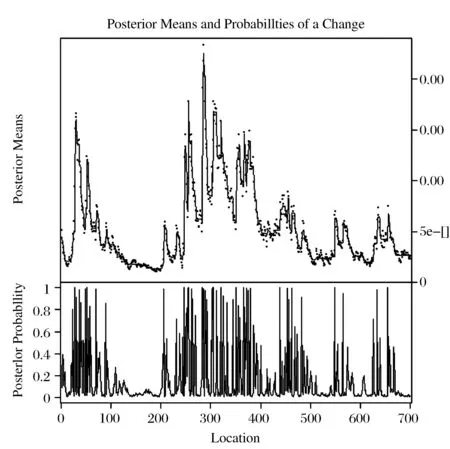
图2 现货条件异方差
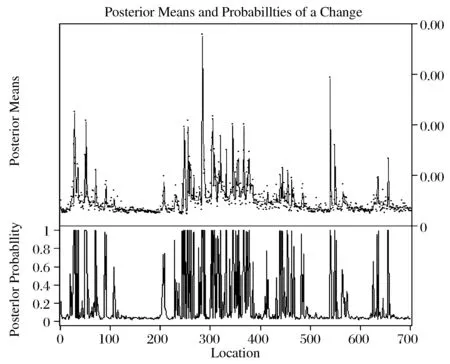
图3 期货条件异方差
根据上图对DCC-GARCH模型的拟合结果进行分析,可以发现DCC-GARCH模型的条件方差序列存在明显的高波动率区域和低波动率区域,条件方差在这两种状态之间频繁波动,即存在区制转移效应。可见DCC-GARCH模型不能够完全消除波动率的集聚效应,因此可以考虑引入区制转移模型对现货与期货序列进行分析,考察资产价格序列及其条件方差序列在两个状态之间的波动,即高波动率及低波动率两个状态,据此建立MRS-DCC模型。
3.2.3 各模型的拟合结果
根据理论部分的推导,对各模型进行拟合,其中MRS-DCC是运用MATLAB中的条件最优化函数拟合得到。
由表3A、3B可以看出各模型的参数显著性状况较好,模型的可靠性可以得到保证,同时MRS-DCC模型两状态的参数均基本显著,因此可以说明区制转移效应是显著存在的。
3.2.4 各模型套期保值效果比较。
为了比较各模型的套期保值效果,根据上文的式(9),计算各模型得到的套期保值比率,进而运用式(30),计算各个模型样本内的套期保值绩效,如表4。
为了进行样本外的套期保值绩效的比较,我们将滚动样本计算出最后一个样本日的套期保值比率,作为下一交易日的套期保值比率,结果如表5,可以看到MRS-DCC方法在样本外的检验结果也是优于其他几个模型的。因此,MRS-DCC在样本内核样本外都能够获得显著优于其他套期保值方法的结果。
由于在比较不同模型的套期保值绩效时使用的评估方法为:
因此当比较不同收益率之间的套期保值绩效时,评估套期保值绩效的方式应该修改为:

表3 各模型参数估计结果
注:*、**及***分别表示在10%、5%及1%的显著性水平下显著。
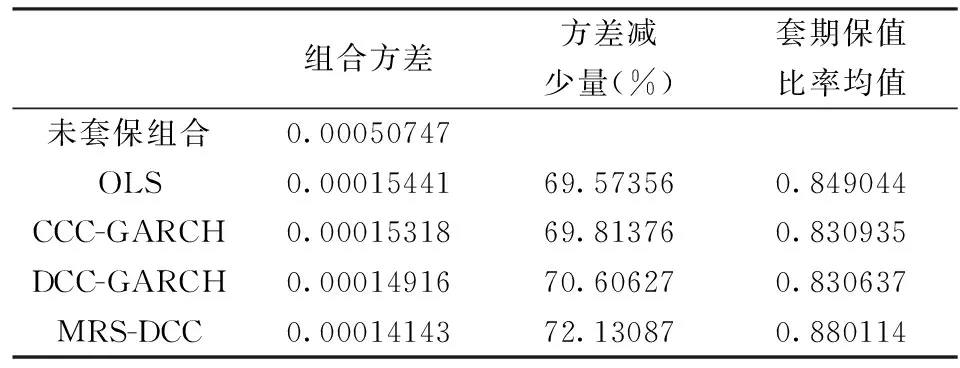
表4 样本内套期保值绩效的比较(MV)
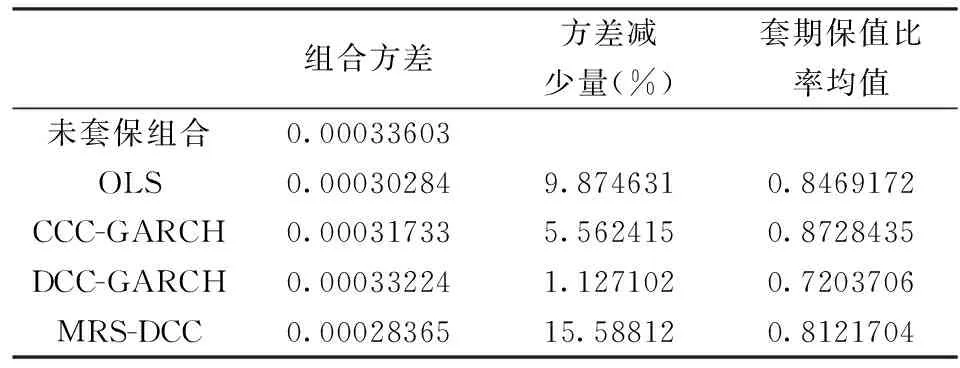
表5 样本外套期保值绩效的比较(MV)
从而保证两种收益率估计得到的套期保值比率在统一标准下比较。

表6 不同收益率绩效的比较(MV)
3.2.5 实证结果分析
从套期保值效果来看,铜品种的组合方差的减少量从大到小,即套期保值绩效从优到劣依次均为:MRS-DCC、DCC-GARCH、CCC-GARCH、OLS。而由套期保值比率均值衡量的建仓的成本从大到小依次为MRS-DCC、DCC-GARCH、OLS、CCC-GARCH。据此我们可以得到以下结论。
(1)通过对比OLS模型与未套保组合的组合方差可以看到,套期保值的引入对于减少投资组合方差的作用是显著的,通过套期保值能够降低组合风险,减小投资者的风险敞口,使投资者能够更好地应对资产价格的异常波动,从而减少损失。然而,期货市场上的对冲交易带来的建仓成本会在一定程度上削弱由套期保值带来的风险降低方面的收益。
(2)通过对比CCC-GARCH与OLS模型的结果,可以发现GARCH模型的引入在一定程度上提高了套期保值的绩效,并且CCC-GARCH模型的套期保值比率均值低于OLS,表明建仓成本有所降低。因此CCC-GARCH相对于OLS,能够为投资者带来的更高的收益。
(3)比较DCC-GARCH与CCC-GARCH可以发现,动态相关系数的引入对于套期保值绩效的提高是明显的,但是DCC-GARCH模型的套期保值比率均值相对较高,即带来了较高的建仓成本。因此DCC-GARCH模型应用于套期保值,为投资者带来的收益会受到一定程度的影响。
(4)MRS-DCC模型相对于其他三个模型,其套期保值绩效最优,但由套期保值比率均值衡量的建仓成本也是最高的。因此在铜期货品种中,MRS-DCC模型对于投资者套期保值收益的提高是极为明显的,虽然它会带来较高的建仓成本,但考虑到MRS-DCC的套期保值绩效是最高的,因此区制转移效应的引入,在铜品种的套期保值中仍能起到很重要的作用。
通过样本外各模型套期保值绩效的比较,我们可以发现,MRS-DCC在减少风险方面仍然是优于其他模型的,进一步说明了MRS-DCC模型能够有效地指导套期保值策略的制定,为套期保值者提供了比OLS、CCC-GARCH和DCC-GARCH模型更佳的套期保值效果。
根据表6中不同收益率套期保值绩效的比较,我们可以发现,使用极差收益率可以获得比普通日间收益率更好的套期保值效果,并且因为极差收益率的引入能够使得投资者在日内实时观察调整自己头寸,就不会发生收盘或者即将收盘时来不及进行头寸的调整的问题。
4 结语
套期保值作为期货市场最重要的功能之一,一直是国内外研究的重点。本文将区制转移效应引入套期保值模型构建中,并基于极差收益率对铜期货品种进行了实证研究。
实证结果表明,区制转移效应的引入对于提高套期保值绩效有着较为显著的作用,将套期保值中的现货与期货价格序列的波动性分解为高波动性及低波动性两个区制,消除了GARCH模型中所普遍存在的波动率高持续性,从另一个角度解释了波动率的集聚性,比单纯的GARCH模型能够更准确地反映收益率波动的规律,从而获得了更优的套期保值绩效。
同时本文将极差收益率引入套期保值领域,这不仅能够更好地刻画真实波动率,并且在期货保证金制度下,由于投资者更加关注每日最高价格与最低价格带来的对其保证金头寸带来的冲击,因此相比于传统的日间收益率,日内极差收益率能够更加准确和直观地指导投资者进行每日头寸调整,在实际运用中更有前景。
样本内与样本外的实证结果也证明了加入了区制转移效应的DCC-GARCH模型能够有效地提高套期保值绩效,同时极差收益率的引入也被证明了能够获得比传统日间收益率更好的模型拟合效果。
考虑到区制转移效应对于套期保值绩效显著的提高作用,未来能够在这方面做进一步的研究,包括将MRS模型与ECM-GARCH等传统套期保值模型结合,从而得到更好的套期保值效果,另外由于极差和日间收益率均存在价格先波动,套期保值再进行后验分析的问题,因此未来研究更多的预测性套期保值方法。
[1]JohnsonLL.Thetheoryofhedgingandspeculationincommodityfutures[J].RiskUncertainty&Profit, 1960, 27(2):297-298.
[2]EderingtonLH.Thehedgingperformanceofthenewfuturesmarkets[J].JournalofFinance, 1979, 34(1):157 -170.
[3]ParkHY,BeraAK.Interest-ratevolatility,basisriskandheteroscedasticityinhedgingmortgages[J].RealEstateEconomics, 1987,volume15(2):79-97(19).
[4]EngleR.Autoregressiveconditionalheteroscedasticitywithestimatesofthevarianceofunitedkingdominflation[J].Econometrica,1982(4):987-1007.
[5]BollerslevT.Modellingthecoherenceinshort-runnominalexchangerates:amultivariategeneralizedarchmodel[J].TheReviewofEconomicsandStatistics,1990,72(3):498-505.
[6]TseYK,TsuiAKC.Amultivariategeneralizedautoregressiveconditionalheteroscedasticitymodelwithtime-varyingcorrelations[J].JournalofBusiness&EconomicStatistics,2002(3):351-362.
[7]LamoureuxCG,LastrapesWD.Persistenceinvariance,structuralchange,andtheGARCHmodel[J].JournalofBusiness&EconomicStatistics,1990(2):225-234.
[8]FongWM,SeeKH.Amarkovswitchingmodeloftheconditionalvolatilityofcrudeoilfuturesprices[J].EnergyEconomics,2002:71-95.
[9]AlizadehAH,NomikosNK.Amarkovregimeswitchingapproachforhedgingstockindices[J].TheJournalofFuturesMarkets,2004(7):649-674.
[10]LeeHT,YoderJ.Optimalhedgingwitharegime-switchingtime-varyingcorrelationGARCHmodel[J].TheJournalofFuturesMarkets,2007(5): 495-516.
[11]LeeHT,YoderJ.AbivariatemarkovregimeswitchingGARCHapproachtoestimatetimevaryingminimumvariancehedgeratios[J].AppliedEconomics,2007:1253-1265.
[12] 付胜华,檀向球.股指期货套期保值研究及其实证分析[J].金融研究,2009(4):113-119.
[13] 付剑茹,张宗成. 时变最优套期保值比估计及比较研究——基于卡尔曼滤波在状态空间模型中的应用[J].管理科学学报,2010(12):23-33.
[14] 彭红枫,叶永刚.基于修正的ECM-GARCH模型的动态最优套期保值比率估计及比较研究[J].中国管理科学,2007(5):29-35.
[15]KronerKF,SultanJ.Time-varyingdistributionsanddynamichedgingwithforeigncurrencyfutures1993(28).
[16] 王辉,孙志凌,谢幽篁.中国农产品期货套期保值非对称效应研究[J].统计研究,2012(7):68-74.
[17] 赵鹏, 曾剑云. 我国股市周期性破灭型投机泡沫实证研究——基于马尔可夫区制转换方法[J]. 金融研究, 2008, 25(4):174-187.
[18] 朱孟楠,刘林,倪玉娟.人民币汇率与我国房地产价格——基于Markov区制转换VAR模型的实证研究[J].金融研究,2011(5):58-71.
[19]ParkinsonM.Theextremevaluemethodforestimatingthevarianceoftherateofreturn[J].TheJournalofBusiness,1980(1):61-65.
[20]AndersenTG,BollerslevT.Answeringtheskeptics:yes,standardvolatilitymodelsdoprovideaccurateforecasts[J].InternationalEconomicReview, 1998, 39(4):885-905.
[21]Mapa,JonesDS.Arange-basedGARCHmodelforforecastingvolatility[J].ThePhilippineReviewofEconomics,2003(2 ):73-90.
[22]GraySF.Modelingtheconditionaldistributionofinterestratesasaregime-switchingprocess[J].JournalofFinancialEconomics, 1996, 42(1):27-62.
TheEstimationofOptimalHedgingRatioofCopperFutureMarketofChina——BasedonMarkovRegime-SwitchingGARCHModel
PENG Hong-feng,CHEN Yi
(School of Economics and Management, Wuhan University, Wuhan 430072,China)
GARCH model is being widely used in the research of hedging. However, in some recent empirical analysis, the application in estimation of hedging ratio of this model has been proved to be defective.The high persistence of conditional variance in GARCH model affect the accuracy of the description of asset price series. The Markov Regime-Switching is applied into the construction of hedging model in this paper.The MRS-DCC model which combines MRS model with DCC-GARCH model is established. Using this new model, the hedging ratio of copper futures market is estimated. Meantime, the range yields instead of intraday yields is used as the mark yields to estimate the hedging ratio innovatively. Range yields can reflect the variance of target asset price accurately and help the investor hold the risk of changing of margin position. The using of range yields conform to the real demand of hedging strategy. The method of combination of MRS model and DCC-GARCH model is explained theoretically. With the empirical analysis of copper futures market,from October 15, 2007 to October 15, 2010, in both in-sample and out-sample method, it is proved that the introduction of the Markov regime-switching and range yields improves the accuracy of the estimation of hedging ratio and the hedging performance.The reference for state dependent hedging strategy and measurement of volatility risk of asset price are prouided.
hedging ratio; markov regime-switching; range yield
1003-207(2015)05-0014-09
10.16381/j.cnki.issn1003-207x.2015.05.003
2013-06-05;
2013-11-27
教育部哲学社会科学研究重大攻关项目(12JZD029);教育部人文社科研究项目(12YJC790064);武汉大学“70”后学者学术团队项目及武汉大学自主科研项目(人文社会科学);中央高校基本科研业务费专项资金资助项目
彭红枫(1976-),男(汉族),江西奉新人,武汉大学经济与管理学院教授,博士生导师,研究方向:金融工程、金融计量分析.
F830
A
——基于MS-VAR模型

