中国金融市场动态相关性实证分析
周德才,何宜庆,卢晓勇,张元桢
(南昌大学 经济与管理学院,南昌330031)
0 引言
近些年来,随着金融全球化、自由化的迅速发展,国内外金融市场的联系更加密切,从而推动了金融市场之间动态相关性研究,成为了货币金融理论与实证分析中的热点问题之一。
学者们已经普遍接受了金融市场之间存在较强的相关性的事实(King和 Wadhwani 1990;Longin和 Solnik,1995)[1-2]。目前,金融市场之间的相关性研究方法主要采用线性方法,较少见非对称方法。国内外学者主要使用的协整分析、格兰杰检验、多元GARCH模型等线性方法,主要是检验系数的平稳性,而没有考虑样本数据中存在的非对称性、条件异方差、尖峰厚尾等非对称和结构变化特征,导致这些方法的检验结果则可能出现偏差。另外,学者们主要考察的是国内外的股票市场,忽略了对其他金融市场的考察。因此,本文基于MRS-DCC-MVGARCH模型,选择货币市场、外汇市场、股票市场和债券市场,实证分析中国金融市场之间的动态相关性。
1 MRS-DCC-MVGARCH模型
Engle(2002)提出了 DCC(Dynamic Conditional Correlation)多元变量GARCH模型。该模型解决了大量随时间变动的条件方差协方差矩阵在计算上的复杂性,能够使多个变量之间的相关性估计更加简化,并且可以得到不同变量之间的动态时变的相关系数[3]。
1.1 向量GARCH(p,q)模型

向量GARCH模型可以研究多个市场之间的波动溢出效应,模型中的参数矩阵Aj,Bj中的对角线元素反应了方差、协方差序列自身的相关关系,而非对角线元素则反映不同变量的方差序列,协方差序列之间的相互影响。该模型具有很好的经济意义,但是由于模型参数较多,因而制约了其应用,通常情况下使用其简化形式。
1.2 动态条件相关(DCC)向量GARCH模型的具体形式和参数估计
1.2.1 动态条件相关(DCC)向量GARCH模型的具体形式


1.2.2 动态条件相关(DCC)向量GARCH模型的参数估计
Engle,Sheppard(2001)提出了对DCC-MVGARCH模型的简化估计方法[4],即通过两步来估计:首先估计单变量GARCH模型;其次根据第一阶段所估计出的标准化残差,来估计第二阶段动态条件相关性的参数。可以将需要估计 的 模 型 参 数 θ 分 为 两 部 分 :θ=(φi,ψ),其 中φi=(ωi,α1i,α2i…,αpii,β1,i,β2,i,…,βqi,i)是由第一阶段所估计出来的单变量GARCH模型的参数;ψ则为第二阶段所估计出来DCC模型的参数αm,βn。
由于第一阶段的参数估计与Rt无关,于是在似然函数中用一个k×k单位矩阵Ik代替Rt,第一阶段单变量LARCH模型的似然函数就可以表示为:

1.3 MRS-DCC-MVGARCH模型
1.3.1 MRS-DCC-MVGARCH模型的具体形式
参照Billio,Caporin(2005)[5],本文对DCC-MVGARCH模型做修改,对第二阶段要估计的参数进行马尔科夫区制转移变换,具体形式如下:

1.3.2 MRS-DCC-MVGARCH模型的参数估计
与Billio,Caporin(2005)一样,本文将马尔科夫区制转移结构限制于动态相关系数上,从而消除了其对方差的任何影响[5]。这个限制使得本文可以采用与DCC-GARCH模型一样的两步法估计参数,第一步与前面一样,这里不赘述,下面直接进入第二步。
对区制转移和动态相关系数一起出现的方程式(7)直接进行估计是非常困难的,因为无法使用哈密尔顿滤波(Hamilton filter)。考虑到Qt是不可观察的,将方程(7)修改如下:


2 MRS-DCC-MVGARCH模型的实证分析
2.1 样本数据的选取和处理
本文选择中国7天同业拆借利率、人民币兑美元汇率、上证综合股票指数和中信标普全债指数分别表征货币市场、外汇市场、股票市场和债券市场。数据来自中经网数据库和中信指数服务公司网站。样本区间为2005年7月28日到2013年3月29日的日数据,剔除日期不匹配的数据后,共1865组样本数据。
在实证分析中,本文采用的收益率为对数收益率。假设第i个金融市场在t时刻的价格为Sit,则其对数变化率r′it定义为:

式子中,r′it(i=1,2,3,4)分别表示货币市场(RR)、外汇市场(EE)、股票市场(SS)和债券市场(BB)的收益率。
2.2 数据的统计特征描述
下面使用Eviews 7.0软件,对四个金融市场收益率序列进行统计描述,其结果见表1。从表1可知,四个金融市场的收益率样本的偏态和峰度都显著异于正态的值,J-B统计量在1%的水平上都不显著,表明四个收益率序列都呈现尖峰厚尾的非正态性特征,这一结论与许多关于国内外金融数据的研究结果一致;由Q(20)和Q2(20)值可知,四个收益率系数都在1%置信水平上显著,即它们都存在序列相关,说明波动存在长记忆性和集聚性,可以引入GARCH模型刻画这种时变特征;由均值和标准差比较可知,股票收益率的标准差最大,债券收益率的标准差最小,说明中国股票市场的波动性最大,债券市场波动率最小。

表1 金融市场收益率序列的统计描述
2.3 MRS-DCC-MVGARCH模型的参数估计
2.3.1 单变量GARCH(1,1)模型的估计结果
MRS-DCC-MVGARCH的参数通过两步估计出来,第一步是识别和估计各残差序列的单变量LARCH效应,第二步是在各残差序列标准化后的基础上,估计其条件相关系数。由于众多的实证研究结果均表明,GARCH(1,1)模型可以很好地刻画金融资产收益率的特征,因此,对于单变量GARCH模型的估计,本文采用了最为简洁的GARCH(1,1)模型。同理,在马尔科夫动态条件相关结构的估计中,本文也采用MRS(2)-DCC(1,1)模型。为了研究的方便,均值方程采用rt=r′t-μ的形式,第一阶段部分采用GARCH(1,1)模型对均值方程残差序列进行建模,运行结果在MATLAB7.0上实现,具体如表2所示。α表示ARCH(1)参数估计量,β为GARCH(1)参数估计量。α值越大,说明数据的变动性较小,β值越大说明数据的变动性就越大。具体结构见表2,从表2可知,金融市场每个GARCH(1,1)模型的α>0,β>0,α+β<1,且都在1%的显著水平上显著,表明模型估计正确,符合实际意义。

表2 单变量GARCH(1,1)模型的参数估计
2.3.2 MRS(2)-DCC(1,1)模型的估计结果
对第一阶段估计的结果,把残差经过标准化处理之后,进入第二阶段估计,估计结果如表3所示。从表3可知,金融市场每个MRS(2)-DCC(1,1)模型的α>0,β>0,α+β<1,且都在1%的显著水平上显著,表明模型估计正确,符合实际意义。两种区制的参数估计结果差别很大,说明我国金融市场在2005年以来出现了一下结构变化,需要采用MRS-DCC-MVGARCH来刻画它们之间的动态相关关系。

表3 MRS(2)-DCC(1,1)模型的参数估计
2.3.3 区制概率和区制转移概率
从图1可以看出来,区制1可能的概率区间是2007年年中到2007年底和2010年底,结合表4中所示的区制转移概率矩阵,区制1自身的持续概率为0.42,稳定性不太高,这个阶段恰好是我国金融市场进入熊市的阶段,因此基本可以判断出区制1反映的是我国金融市场处于熊市区制。而从图2中可以发现,区制2最有可能的概率区间是2005年年中到2007年年初到2008年年初和2009年年初到2010年中,结合表4中所示的区制转移概率矩阵,区制1自身的持续概率为0.13,稳定性非常低,这些阶段恰好是我国金融市场进入牛市的阶段,因此基本可以判断出区制1反映的是我国金融市场处于牛市区制。从图1和图2可知,从2010年底到2013年初,我国金融市场处于区制1和区制2相互频繁转移时期,结合表4,我国金融市场在区制1和区制2相互转移的概率分别是0.58和0.87,稳定性高,特别是区制1向区制2转移的概率高达0.87,非常稳定,说明我国金融市场从熊市向牛市转换的时间特别长,符合我国的实际情况。

表4 区制转移概率矩阵

图1 区制1的平滑概率

图2 区制2的平滑概率
2.3.4 各个金融市场之间动态相关系数的实证分析
下面根据表5和图3-8,分析中国各个金融市场之间的动态相关情况。其中,RREE1、RRSS1、RRBB1、EESS1、EEBB1、SSBB1分别表示货币市场(RR)和外汇市场(EE)、货币市场(RR)和股票市场(SS)、货币市场(RR)和债券市场(BB)、外汇市场(EE)和股票市场(SS)、外汇市场(EE)和债券市场(BB)、股票市场(SS)和债券市场(EE)在区制1下的相关系数;RREE2、RRSS2、RRBB2、EESS2、EEBB2、SSBB2表示货在区制2下的相关系数。
①货币市场与外汇市场之间的动态相关系数实证分析。从表5和图3可知,货币市场与外汇市场之间的动态相关系数在所有市场中绝对值最小,均值都是-0.042,说明货币市场与外汇市场之间的动态相关性明显;同时在区制1下的相关程度在-0.0634~-0.0183之间浮动,在区制2下相关程度在-0.0852~+0.0101之间浮动,在区制2和区制1下标准差分别为0.0037和0.0053,说明我国货币市场与外汇市场之间的动态相关系数的波动幅度和强度在区制1(牛市)下都大于区制2(熊市),呈现明显的非对称特征。
②货币市场与股票市场之间的动态相关系数实证分析。从表5和图4可知,货币市场与股票市场之间的动态相关系数货币市场与股票市场之间的动态相关系数在区制1和区制2下均值分别为0.0517和0.0516,非常接近,说明货币市场与股票市场之间的动态相关性明显;同时在区制1下的相关程度在+0.0222~-0.1444之间浮动,在区制2下相关程度在+0.0051~+0.2542之间浮动,在区制1和区制2下标准差分别为0.0050和0.0075,说明我国货币市场与股票市场之间的动态相关系数的波动幅度和强度在区制2(牛市)下都大于区制1(熊市),呈现明显的非对称特征。
③货币市场与债券市场之间的动态相关系数实证分析。从表5和图5可知,货币市场与债券市场之间的动态相关系数货币市场与债券市场之间的动态相关系数在区制1和区制2下均值都为-0.0992,说明货币市场与债券市场之间的动态相关性明显;同时在区制1下的相关程度在-0.1962~-0.0743之间浮动,在区制2下相关程度在-0.2089~-0.0597之间浮动,在区制1和区制2下标准差分别为0.0051和0.0069,说明我国货币市场与债券市场之间的动态相关系数的波动幅度和强度在区制2(牛市)下都大于区制1(熊市),呈现明显的非对称特征。
④外汇市场与股票市场之间的动态相关系数实证分析。从表5和图6可知,外汇市场与股票市场之间的动态相关系数外汇市场与股票市场之间的动态相关系数在区制1和区制2下均值分别为0.0892和0.0891,非常接近,说明外汇市场与股票市场之间的动态相关性明显;同时在区制1下的相关程度在+0.0522~+0.1060之间浮动,在区制2下相关程度在+0.0041~+0.1187之间浮动,在区制1和区制2下标准差分别为0.0039和0.0055,说明我国外汇市场与股票市场之间的动态相关系数的波动幅度和强度在区制2(牛市)下都明显大于区制1(熊市),呈现明显的非对称特征。
⑤外汇市场与债券市场之间的动态相关系数实证分析。从表5和图7可知,外汇市场与债券市场之间的动态相关系数外汇市场与债券市场之间的动态相关系数在区制1和区制2下均值分别为-0.0623和-0.0622,非常接近,说明外汇市场与债券市场之间的动态相关性明显;同时在区制1下的相关程度在-0.1719~-0.0322之间浮动,在区制2下相关程度在-0.3012~-0.0207之间浮动,在区制1和区制2下标准差分别为0.0053和0.0078,说明我国外汇市场与债券市场之间的动态相关系数的波动幅度和强度在区制2(牛市)下都明显大于区制1(熊市),呈现明显的非对称特征。
⑥股票市场与债券市场之间的动态相关系数实证分析。从表5和图8可知,股票市场与债券市场之间的动态相关系数股票市场与债券市场之间的动态相关系数在区制1和区制2下均值分别为0.0914和0.0913,非常接近,说明股票市场与债券市场之间的动态相关性明显;同时在区制1下的相关程度在+0.0372~-0.1227之间浮动,在区制2下相关程度在-0.0278~+0.1532之间浮动,在区制1和区制2下标准差分别为0.0046和0.0066,说明我国股票市场与债券市场之间的动态相关系数的波动幅度和强度在区制2(牛市)下都明显大于区制1(熊市),呈现明显的非对称特征。
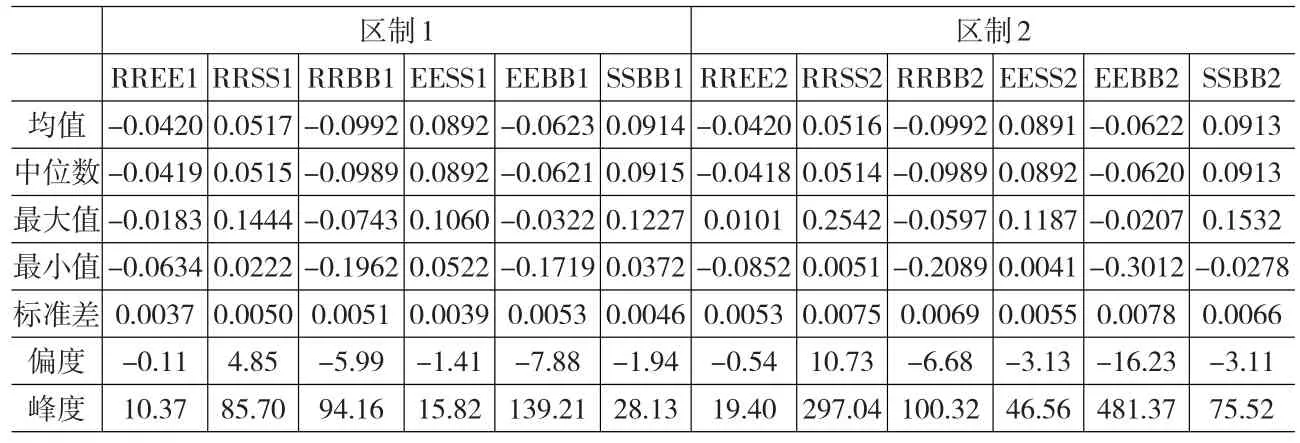
表5 动态相关系数统计表

图3 货币市场与外汇市场动态先关系数

图4 货币市场与股票市场动态相关系数

图5 货币市场与债券市场动态相关系数

图6 外汇市场与股票市场动态相关系数
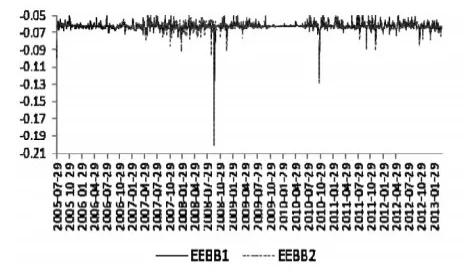
图7 外汇市场与债券市场动态相关系数
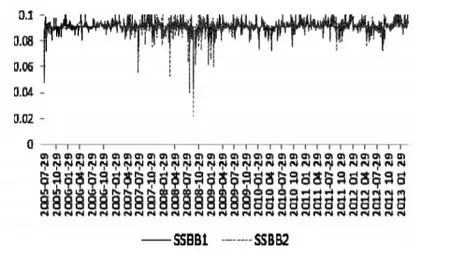
图8 股票市场与债券市场动态相关系数
3 结论
本文在DCC-MVGARCH模型的基础上,对其系数和无条件相关系数引入马尔科夫区制转移结构,构建了MRS-DCC-MVGARCH模型,采用该模型对中国货币市场、外汇市场、股票市场和债券市场之间的动态相关性问题进行了实证分析,研究结果如下:
(1)中国金融市场之间存在明显的动态相关关系。中国货币市场、外汇市场、股票市场和债券市场之间所有的动态相关系数的绝对值均值都大于0.01,最小的是货币市场与外汇市场,均值为0.042,最大的是货币市场与债券市场,均值为-0.992,这说明中国金融市场之间存在明显的动态相关系数。
(2)中国金融市场之间动态相关关系呈现明显的非对称特征。中国货币市场、外汇市场、股票市场和债券市场之间所有的动态相关系数的波动幅度和强度在区制2(牛市)明显比区制1(熊市)下大得多,呈现明显的非对称特征。
总之,中国货币市场、外汇市场、股票市场和债券市场之间存在显著的动态相关关系,说明这四个金融市场是相互影响的,特别是金融市场风险会相互传染,因此,政府在宏观管理,以及企业和个人在金融风险管理和投资过程中,应该考虑这种动态情况。
[1]King M A,Sushil W.Transmission of Volatility Between Stock Markets[J].Review of Financial Studies,1990,(3).
[2]Longin F,Solnik B.Is the Correlation in International Equity Returns Constant:1960-1990[J].Journal of International Money and Financ,1995,(14).
[3]Engle R F.Dynamic Conditional Correlation:A Simple Class of Multivariate LARCH Models[J].Journal of Business and Economic Statistics,2002,(20).
[4]Engle R F,Sheppard K.Theoretical and Empirical properties of Dynamic Conditional Correlation Multivariate GARCH[C].NBER Working Papers 8554,National Bureau of Economic Research,Inc.,2001.
[5]Billio M,Caporin M.Multivariate Markov Switching Dynamic Conditional Correlation GARCH Representations for Contagion Analysis[J].Statistical Methods and Applications,2005,14(2).
——基于MS-VAR模型

