Granger因果关系ECM-DM检验与LA-VAR检验有限样本性质的比较

靳庭良

（河南财经政法大学 经济学院，郑州 450002）

0 引言

Granger因果关系检验是由 Granger（1969）提出，由Sims（1972）推广的反映一（组）变量是否有助于预测另一（组）变量的统计检验方法。其基本检验程序是基于VAR模型的F检验，该检验适合于（趋势）平稳变量之间的检验问题。考虑到经济问题中许多变量呈现出非平稳的特征，非平稳或单整变量之间Granger因果关系的检验问题越来越多地引起了计量经济学家们的关注。一些学者（如，Ohanian，1988；Sims等，1990；Toda和Phillips，1993a；He和Maekawa，2001）研究了序列的非平稳性对Granger因果关系检验的影响。结果表明：当待检验的变量部分或全部为随机游走过程时，上述F检验的统计量可能不再具有标准的极限分布。此时应用F检验法检验变量之间的Granger因果关系很可能会得到错误的结论。进而提出了一些关于非平稳变量之间的Granger因果关系检验程序。例如，针对存在协整关系的I(1)变量，Engle和Granger（1987）给出了利用ECM模型进行检验的两步程序（简称为EGTS检验）、Sims等（1990）提出的在一定条件下直接利用水平VAR模型实施通常的Granger因果关系的检验程序（简称为SSW检验）、Toda和Phillips（1993b，1994）提出的基于Johansen-类型的误差修正模型及最大似然估计的Granger因果关系的序贯检验程序（sequential test procedures）等等；针对一般单整变量，Toda和Yamamoto（1995）提出的不考虑变量之间的协整性直接基于扩展的水平VAR模型进行检验的一般检验程序（简称为LA-VAR检验）、靳庭良（2013）通过扩展EGTS检验提出的基于ECM模型或差分模型(DM)适用于一般单整变量（含I(0)）的检验程序（以下简称为ECM-DM检验）等。

综观上述各种检验方法，它们依据的都是基于统计量的极限分布建立起来的，换言之，它们在理论上是适合于大样本下的检验。然而，从实践的观点，对基于渐近理论建立起来的Granger因果关系检验程序都必须研究它们的有限样本性质，以评价其稳健性及检验的功效。因此，本文主要针对单整变量，利用Monte Carlo模拟试验研究ECM-DM检验的有限样本性质，并与LA-VAR检验的有限样本性质进行对比分析。

1 基本理论

变量之间Granger因果关系检验的基本方法是基于如下VAR模型（1）的F检验：

其中误差项向量ut=(u1t，u2t)′为白噪声过程，即ukt（k=1,2）满足：E(ukt)=0，Var(ukt)=σk2，Cov(ukt,uhs)=0（k,h=1,2,t≠s）。具体而言，就是在利用OLS法估计模型（1）的基础上，使用通常的检验参数线性约束的F统计量，分别检验如下两个原假设：

原假设HY→X：β1j=0（j=1，2，…，p）（Y不是X的Granger原因）；

和

原假设HX→Y：α2j=0（j=1，2，…，p）（X不是Y的Granger原因）。

此时，针对原假设HY→X的统计量为

和无约束模型，即模型（1）的第一个方程，利用OLS法估计得到的残差平方和。在HY→X成立的条件下，FY→X渐近服从F(p，n-2p-1)分布。于是，对于给定的显著性水平α，可以查F分布表得临界值 Fα(p，n-2p-1)，将其与统计量FY→X的样本值进行比较，便可以判断原假设HY→X是否显著成立。

对于原假设HX→Y，可以类似地进行检验。值得注意的是，利用模型（1）进行因果关系检验，要求变量都是平稳的或趋势平稳的，当变量中含有单整变量时，F检验通常是失效的。

1.1 ECM-DM检验程序

通过分析已有利用ECM模型或DM模型对单整变量之间进行Granger因果关系检验的方法的局限性，靳庭良（2013）提出了适用于一般单整变量（含I(0)变量）之间Granger因果关系的ECM-DM检验程序。具体分为如下三种情形：

（1）对于存在一般协整关系的单整变量，可以按照扩展的Engle和Granger（1987）两步检验法进行检验。具体又分为如下三种情形：

情形1 d阶单整变量之间存在（d,d）阶协整关系。例如，对于2阶单整变量Xt与Yt，若它们之间存在(2,2)阶协整关系：Yt=λXt+vt，或Xt=(1/λ)Yt-(1/λ)vt，vt～I(0)，则可以利用误差修正模型

情形2 d阶单整变量之间存在（d,b）(d＞b)阶协整关系，并且非均衡误差项与某一变量的差分之间具有协整关系。例如，对于2阶单整变量Xt与Yt，若Xt与Yt之间存在(2,1)阶协整关系：Yt=λXt+vt，或 Xt=(1/λ)Yt-(1/λ)vt，vt～I(1)，并且 Yt-1-λXt-1与 ΔXt-1（或 ΔYt-1）具有协整关系：Yt-1-λXt-1=δΔXt-1+wt，则可以利用模型

（3）对于不同阶的单整变量（含I(0)变量），可以通过差分变换降低较高阶单整变量的阶数，转变为具有同阶单整变量的情形进行检验。例如，若Xt和Yt分别为I(2)、I(0)变量，则X与Y之间Granger因果关系可以利用模型

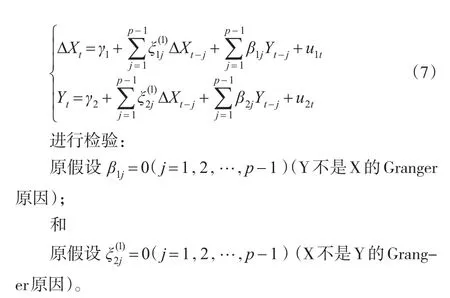
关于ECM-DM检验程序的有限样本性质，目前尚无文献对此进行系统地研究。为行文方便，我们将后两种情形依次记为情形4、情形5。

1.2 LA-VAR检验程序

考虑到已有Granger因果关系的检验方法依赖于变量的单整性和变量之间协整关系的存在性，而这些预检验可能存在严重的偏差，Toda和Yamamoto（1995）提出了基于扩展的VAR模型的F检验，即LA-VAR检验法。该方法只需要知道待检验变量的最高单整阶数dmax，通过估计p+dmax阶VAR模型（称之为扩展的VAR模型，p为VAR模型的真实阶数），并对前p个滞后系数进行通常的F检验，即可完成它们之间Granger因果关系检验的方法。例如，设关于单整变量X、Y的正确的VAR模型为模型（1），其中X、Y的单整阶数最高者为dmax，那么检验此两变量之间Granger因果关系的LA-VAR检验法的基本过程就是，首先建立回归模型

然后利用OLS法估计该模型，使用通常的检验参数线性约束的F统计量，分别检验如下两个原假设：

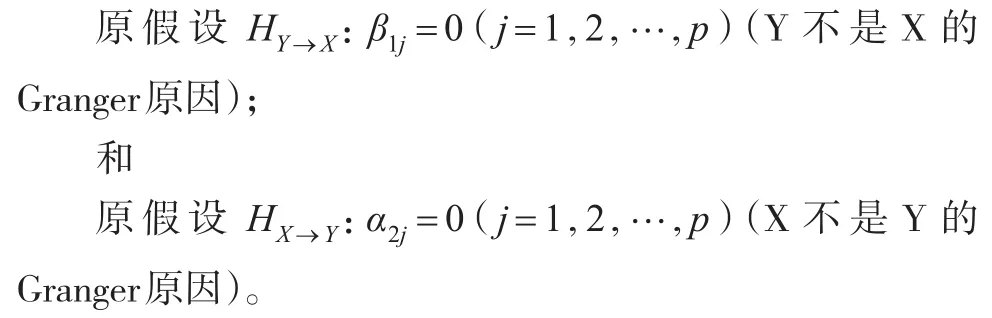
LA-VAR检验法不需要事先知道变量之间是否存在协整关系，应用起来比较方便，在一定程度上也能避免协整关系预检验带来的偏差。但是由于用于检验的VAR模型存在过度拟合会导致该检验遭受势的损失。对于含有I(1)、I(0)的变量，Yamada和 Toda（1998）研究了 Toda and Phillips(1993,1994)提出的基于Johansen-type ECM)的检验、Phillips(1995)提出的FM-VAR检验和LA-VAR检验等三种Granger因果关系检验程序的有限样本性质。结果表明，对于典型的经济时间序列的样本容量，LA-VAR检验的实际检验水平的稳定性好于其他检验，而且随着样本容量的增加，其实际检验水平快速趋近于名义检验水平；一般地，ECM检验在准确检验协整关系的前提下具有满意的表现，但FM-VAR检验对于数据生成过程中参数的设定是敏感的；并且就一般而言，FM-VAR检验和ECM检验具有较高的势，而LA-VAR检验的势最低。

2 试验设计

在计量经济分析中，人们遇到的单整变量的阶数通常不超过2阶，因此在Granger因果关系检验的稳健性和有效性模拟试验中，我们设定单整变量的阶数至多为2，并且与上述ECM-DM检验的五种情形相对应，考虑如下五种数据生成过程（DGP）：

在模拟试验中，设定名义检验水平为0.05、0.01，样本容量T分别取为25、50、100、200，以研究ECM-DM检验与LA-VAR检验的实际检验水平对名义检验水平的偏离程度及它们的势。每次模拟生成样本数据都设定初始值为0，按设定的数据生成过程生成长度为T+200的样本数据，然后去掉前200个数据，以消除初始值对分析结果的影响，重复模拟5000次。为简单起见，情形5对应的回归模型中滞后阶数p=1，其余情形均设定为p=2。所有模拟结果都是在EViews6.0软件下通过编程得到的。结果表明，在名义检验水平为0.05和0.01下所得ECM-DM检验与LA-VAR检验有限样本性质的比较结果是一致的。因此，为行文简便，本文只列出了名义检验水平为0.05的模拟结果。

表1 情形1下两检验的势和实际检验水平

3 有限样本性质

依据前述模拟试验设计，模拟得到情形1至情形5下ECM-DM检验和LA-VAR检验的实际检验水平和势如表1至表5所示。从模拟结果可见，在各种情形下，对于一定的参数值及名义检验水平0.05，样本容量越大，两种检验的势就越高。例如，在情形1下，当η1=0.15，η2=-0.3，T=25、50、100、200时，ECM-DM检验的势分别为0.259、0.522、0.840、0.991；LA-VAR 检 验的 势分别 为 0.191、0.462、0.809、0.989。而且当T值较大时，ECM-DM检验与LA-VAR检验都具有较好的稳健性，即它们的实际检验水平均接近于0.05。例如，当T=200时，在情形1下，ECM-DM检验和LA-VAR检验的实际检验水平分别为0.053、0.052。

另外，从表1还可以看出，在情形1下，ECM-DM检验和LA-VAR检验的实际检验水平均在0.048与0.056之间。此表明它们的实际检验水平与0.05的名义检验水平都非常接近，具有很好的稳健性。当η1或η2的绝对值都较高时，它们的势较高；当η1和η2的绝对值都较低时，它们的势也较低；但当样本容量较小时，ECM-DM检验较LA-VAR检验具有较高的势。例如，当T=100，η1=0.15，η2=-0.3时，ECM-DM检验和LA-VAR检验的势分别为0.840，0.809；当T=100，η1=0.15，η2=0时，两者的势分别为0.244,0.229。

从表2可以看出，在情形2下，当T值较小时，ECM-DM检验的实际检验水平小于名义检验水平0.05，而LA-VAR检验实际检验水平略大于名义检验水平0.05，后者检验水平的扭曲程度低于前者的。例如，当T=25时，它们的实际检验水平分别为0.033、0.058。当η1与η1+η2的绝对值都较高时，ECM-DM检验和LA-VAR检验的势较高，当两者的绝对值之一相同时，另一个的绝对值越高，它们的势越高。例如，当T=100，η1=0.15，η2=0.3时，ECM-DM检验和LA-VAR检验的势分别为0.984，0.979；当 T=100，η1=0.15，η2=0.15时，两者的势分别为0.819,0.804。同时也发现，就整体而言，当两种检验的势均较高时，ECM-DM检验的势高于LA-VAR检验的势。

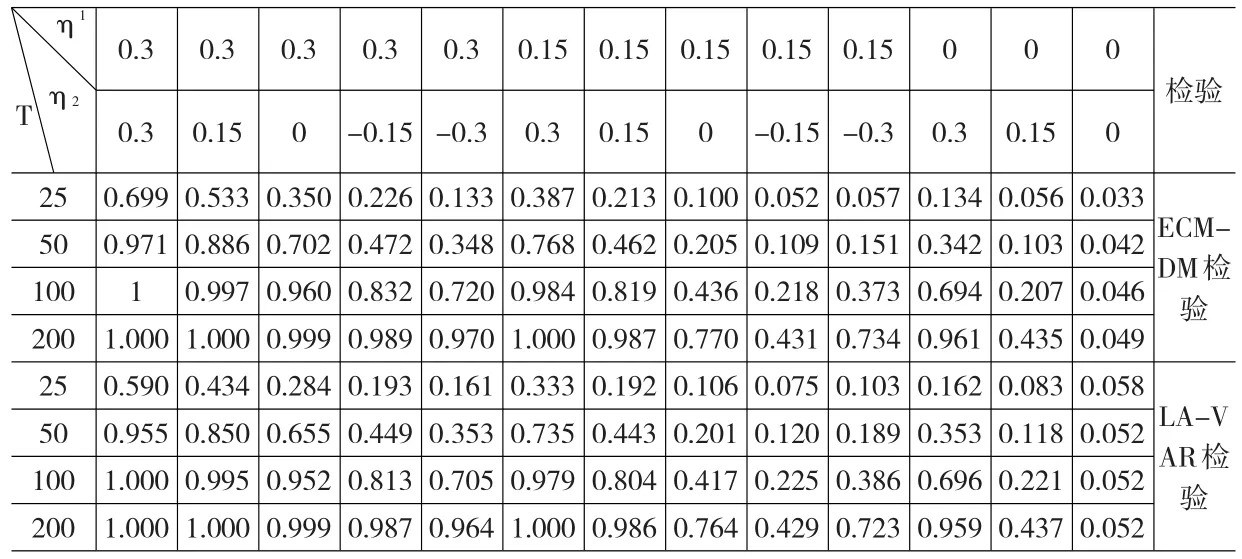
表2 情形2下两检验的势和实际检验水平

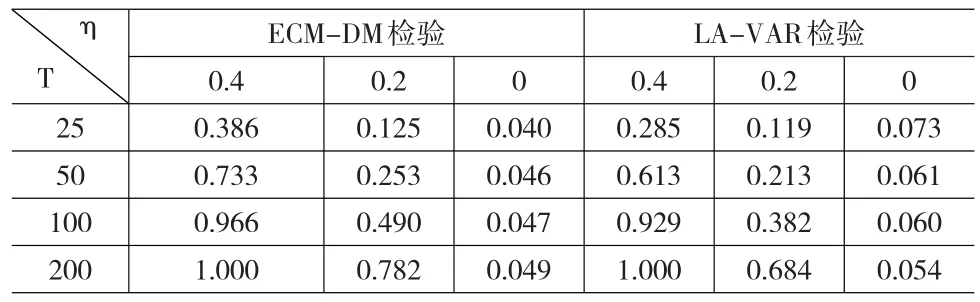
表3 情形3下两检验的势和实际检验水平

从表3可以看出，在情形3下，当T值较小时，ECM-DM检验的实际检验水平小于名义检验水平0.05，LA-VAR检验的实际检验水平大于名义检验水平0.05，相比之下前者检验水平的扭曲程度低于后者的。例如，当T=25时，它们的实际检验水平分别为0.040、0.073。一般地，ECM-DM检验的势远高于LA-VAR检验的。例如，当T=100，η=0.2时，ECM-DM检验和LA-VAR检验的势分别为0.490，0.382。另外，对于一定的T值，随着η的绝对值的增加，两种检验的势均上升。例如，当T=100，η=0.2、0.4时，ECM-DM检验的势分别为0.490、0.966；LA-VAR检验的势分别为0.382、0.929。

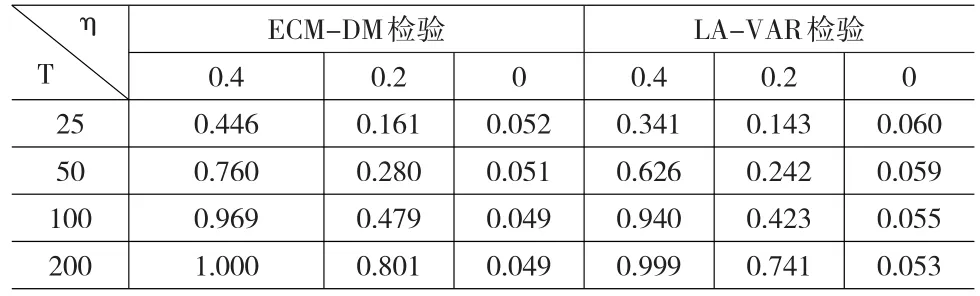
表4 情形4下两检验的势和实际检验水平

从表4可以看出，在情形4下，当T值较小时，ECM-DM检验的实际检验水平与名义检验水平0.05很接近，LA-VAR检验的实际检验水平大于名义检验水平0.05。例如，当T=25时，它们的实际检验水平分别为0.040、0.06。一般地，ECM-DM检验的势明显高于LA-VAR检验的。例如，当T=100，η=0.2时，ECM-DM检验和LA-VAR检验的势分别为0.479，0.423。另外，对于一定的T值，随着η的绝对值的增加，两种检验的势均上升。例如，当T=100，η=0.2、0.4时，ECM-DM检验的势分别为0.479、0.969；LA-VAR检验的势分别为0.423、0.940。

从表5可以看出，在情形5下，当T值较小时，ECM-DM检验与LA-VAR检验的实际检验水平均与0.05的名义检验水平很接近。例如，当T=25时，它们的实际检验水平分别为0.048、0.047。当两者的势均较高时，前者较后者具有较高的势。例如，当T=50，β=0.4时，ECM-DM检验和LA-VAR检验的势分别为0.774，0.747。另外，对于一定的T值，随着β的绝对值的增加，两种检验的势均上升。例如，当T=50，β=0.2、0.4时，ECM-DM检验的势分别为0.269、0.774；LA-VAR检验的势分别为0.245、0.747。

表5 情形5下两检验的势和实际检验水平

4 结论

本文系统研究了Granger因果关系ECM-DM检验的有限样本性质，并与LA-VAR检验的有限样本性质进行了对比分析。Monte Carlo模拟结果表明，对于经济序列典型的样本容量，在ECM-DM检验的各种情形下，样本容量越大，ECM-DM检验和LA-VAR检验的势就越高，即检验的有效性越高；而且当样本容量较大时，ECM-DM检验与LA-VAR检验的实际检验水平均接近于名义检验水平，都具有较好的稳健性。但两种检验的势及当样本容量较小时的稳健性，因样本数据生成过程的不同存在一定的差异：（1）在情形1和情形5下，ECM-DM检验和LA-VAR检验都具有较好的稳健性；在情形4下，ECM-DM检验的实际检验水平接近于名义检验水平，而LA-VAR检验的实际检验水平大于名义检验水平；在情形2和情形3下，ECM-DM检验的实际检验水平小于名义检验水平，而LA-VAR检验实际检验水平大于名义检验水平，但相比之下，在情形2下，后者的稳健性好于前者，在情形3下前者的稳健性要好于后者。（2）一般地，在各种情形下ECM-DM检验较LA-VAR检验具有较高的势。因此，综合比较检验的稳健性和有效性，可知在情形3下宜采用LA-VAR检验法进行检验，在其他情形下，则宜采用ECM-DM检验法进行检验。

需要指出的是，我们上述的结论是在已知变量之间协整关系的前提下得到的，当变量之间的协整关系存在误设时，ECM-DM检验的势可能远低于LA-VAR检验。这一点已被作者进行的模拟试验所证实。

[1]靳庭良,单整变量之间Granger因果关系的一种检验程序[J].数量经济技术经济研究，2013，(2).

[2]Engle R F ，Granger C W J.Co-Integration and Error-correction：Representation,Estimation and Testing[J].Econometrica,1987，55(2).

[3]Granger C W J.Investigating Causal Relations by Econometric Models and Cross-spectral Models[J].Econometrica,1969,37(3).

[4]He Z L,Maekawa K.On Spurious Granger Causality[J].Economics Letters,2001,73(3).

[5]Johansen S.Statistical Analysis of Cointegration Vectors[J].Journal of Economic Dynamics and Control,1988,12(2～3).

[6]Johansen S.Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian vector Autoregressive models[J].Econometrica,1991,59(6).

[7]Nelson C R,Plosser C I.Trends and Random Walks in Macroeconomic Time Series[J].Journal of Monetary Economics,1982,(10).

[8]Ohanian L E.The Spurious Effects of Unit Roots In Vector Autoregressions：a Monte Carlo study[J].Journal of Econometrics,1988,39(3).

[9]Phillips P C B.Fully Modified Least Squares and Vector Autoregression[J].Econometrica,1995,63(5).

[10]Sims C A.Money,Income,and Causality[J].American Economic Review,1972,62(4).

[11]Sims C A，Stock J H,Watsonc M W.Inference in Linear time Series Models with Some unit roots[J].Econometrica,1990,58(1).

[12]Toda H Y,Phillips P C B.The Spurious Effect of Unit Roots on Vector Autoregressions[J].Journal of Econometrics,1993,59(3).

[13]Toda H Y,Phillips P C B.Vector Autoregressions and Causality[J].Econometrica,1993,61(6).

[14]Toda H Y,Yamamoto T.Statistical Inference in Vector Autoregressions with Possibly integrated processes[J].Journal of Econometrics,1995,66(1～2).

[15]Yamada H，Toda H Y.Inference in Possibly Integrated Vector Autoregressive Models：Some Finite Sample Evidence[J].Journal of Econometrics,1998，86(1).