基于广义模糊软集理论的云计算资源需求组合预测研究

徐达宇，杨善林，罗 贺

(1.浙江农林大学浙江省林业智能监测与信息技术研究重点实验室，浙江 杭州 311300；2.合肥工业大学过程优化与智能决策教育部重点实验室，安徽 合肥 230009)



基于广义模糊软集理论的云计算资源需求组合预测研究

徐达宇1,2，杨善林2，罗 贺2

(1.浙江农林大学浙江省林业智能监测与信息技术研究重点实验室，浙江 杭州 311300；2.合肥工业大学过程优化与智能决策教育部重点实验室，安徽 合肥 230009)

论述了云计算资源需求预测的作用，提出了新的基于夹角余弦的广义模糊软集相似性度量方法，将相似性度量结果与预测精度相结合来获得各单项预测模型的权重，并针对云计算环境中资源需求所表现出的短期动态性和长期周期性特征，选用自适应神经模糊推理系统ANFIS和季节性ARIMA模型SARIMA作为单项预测模型，以此构建基于广义模糊软集理论的组合预测模型GFSS-ANFIS/SARIMA。最后将该模型用于云计算环境下的资源需求预测应用中去。实验结果表明，与其它预测模型相比，该模型能有效提高预测精度，具有良好的预测性能。本文所提方法能为云计算资源的高效调度和分配提供决策支持。

云计算；广义模糊软集；相似性度量；组合预测；自适应神经模糊推理系统

1 引言

云计算以承诺向用户提供具有高可扩展性、灵活性和成本效益的计算、存储及其它各类应用服务而受到业界的广泛关注。为了实现这些承诺，云计算服务提供商不仅需要通过构建完善的基础设施、采取迅速有效的管理机制对资源进行规划以提供高质量服务来满足用户需求，同时还需要控制成本、提高利润来谋求自身的长期发展，而云计算数据中心能源消耗所产生的费用是运营成本中一个主要的构成部分。Bianchini[1]指出一台功率为300瓦特的服务器，一年内将用去338美元电费并释放1300千克二氧化碳。相关统计还显示，在2006年，美国全部的数据中心消耗了590亿千瓦时电量，占全社会电力消费的2%，价值共计约41亿美元，截止到2011年这一数据已翻倍，数据中心如此巨大的电力消耗不仅增加了运营商的运营成本，而且还会因高功率运行产生的大量热量导致系统可靠性的降低和设备寿命的减短，继而再次增加运营商固定资本的投入。另一方面，与高电力消耗形成鲜明对比的是数据中心资源的低利用率，研究显示云计算数据中心各类资源(CPU，内存，网络及存储等)的平均利用率在10%至50%之间，超过60%的服务器处于闲置状态[2], 即这些珍贵的资源在大部分时间里未得到充分利用。因而，如何运用相关理论与方法来实现云计算资源的合理使用，建设具有能源意识数据中心，减小其对环境的负面影响，实现绿色计算成为近年来学界的研究热点[3-4]。

云计算环境下的资源需求预测是实现云计算海量异构资源有效管理以应对动态且不确定的多元化用户需求，保证及时、可靠地将各种资源提供给使用者的同时降低运营商、服务提供商自身的成本，以及减少数据中心能源消耗过程中重要的一步。利用历史数据对未来一段时间内资源需求负荷进行准确的预测，就可以运用服务器运行机制和虚拟化技术来实现整个云计算数据中心资源的合理分配，并为云计算运营商提供有力的决策支持。在先前的云计算资源需求预测研究中，相关学者使用了如自回归模型(AR)[5]、模式匹配[6]、神经网络[7-8]等单项方法。然而，云计算资源需求负荷是受多种因素影响的复杂非线性系统，在多因素影响的叠加下，单一模型难以准确描述其复杂的内部变化规律，不能及时反映外部环境因素发生的变化，是预测精度具有非精确性的模糊系统，而组合预测方法能有效结合各种单项预测模型的优点，并能确保其预测误差的方差不大于任何一个单项预测模型[9], 是在现有单项预测模型的基础上再次提高预测精度的理想选择。

Bates和Granger[10]于1969年首次提出组合预测的思想，它综合利用各单项预测方法提供的信息，集成不同信息来源的预测结果, 从而提高预测精度，而组合预测的难点是最优模型组合权重的分配。国内学者提出了一些组合预测模型的权重确定方法，如陈华友等[11]以预测精度作为诱导变量值进行有序加权几何集成，通过预测值对数序列与实际值的对数序列之间的相关程度作为目标函数，提出一种基于相关系数的IWOGA算子最优组合预测模型。孙李红等[12]提出了基于相关系数加权集合平均来确定权重的组合预测方法。李美娟等[13]提出相容方法集和互补模型集，然后在对不同单一预测模型的漂移性和互补性研究的基础上求各种模型权重，构建了基于漂移度的组合预测模型，为组合预测模型研究提供一种新的思路。

然而，如Xiao Zhi等[14]所述，组合预测模型中由各单项模型获得的预测值是对实际值的一个模糊描述，因此基于精确概念的传统数学方法在处理此类问题时就有其不足之处。Molodtsov[15]于1999年提出了模糊软集合(FSS, Fuzzy Soft Sets)理论用于处理嵌入在各类系统中的具有不确定性和非精确性问题，并在系统地定义了其相关法则的基础上列举了一些简单应用。自此，模糊软集合理论有了快速的发展，如Maji等人[16]将该理论运用于解决决策问题，孙智勇和刘星[17]提出了基于模糊软集合理论的税收收入的组合预测模型。在这些研究的基础上,Majumdar和Samanta[18]拓展了模糊软集合理论并提出了广义模糊软集合(GFSS, Generalized Fuzzy Soft Sets)这一概念及其基本性质，给出了广义模糊软集合的相似性度量方法，并用一个医学决策实例验证了该方法的有效性。可以说，广义模糊软集合是模糊软集合的进一步推广，可以更好地处理不确定性问题[19]。

本文介绍了广义模糊软集合的基本概念及其性质，把广义模糊软集合理论引入到组合预测模型的构建当中去，提出了新的基于夹角余弦的广义模糊软集合相似性度量方法，将相似性度量与单项预测模型的预测精度结合，获得组合预测模型的权重系数，从而构建基于广义模糊软集合的组合预测模型，并将该方法用于预测云计算环境下的动态资源需求。在实验中将该组合预测模型与其它预测模型在预测性能上进行了全面的比较，结果显示了该组合预测模型的有效性和可靠性。

2 广义模糊软集合的基本概念

在本节中，首先简单介绍模糊软集合理论，随后给出广义模糊软集合的基本概念。

2.1 模糊软集合理论

定义2.1[15]：设U是初始论域，E是参数集，P(U)是集合U上的幂集，称(F,E)是U上的一个软集合，当且仅当F是E到U的所有子集的一个映射，即F:E→P(U)。

定义2.2[20]：设U是初始论域，E是参数集，设IU为U的所有模糊子集。令A⊂E，则称(F,E)是U上的一个模糊软集合，当且仅当F满足映射关系：F:A→IU。

2.2 广义模糊软集合

在了解了模糊软集合的基本定义后，下面进一步论述广义模糊软集合的定义。

定义2.3[18]：设U={x1,x2,…,xn}为初始论域,E={e1,e2,…em}为对应的参数集,则(U,E)称为软论域。令F为映射F:E→IU,μ为E的一个模糊子集且满足μ:E→I=[0,1],其中IU为U的所有模糊子集集合。再令映射Fμ:E→IU×I,函数Fμ具有以下定义：Fμ(e)=(F(e),μ(e)),其中F(e)∈IU。那么,Fμ就成为软论域(U,E)上的一个广义模糊软集合。

在此，对于任意一个给定的参数ei,Fμ(ei)=(F(ei),μ(ei))不仅用F(ei)给出了U中每一个所考虑对象在某一特定属性下的模糊隶属程度，而且还用μ(ei)指出了这种隶属程度的整体可能性大小。在Majumdar等[18]研究中还给出了两个GFSS之间的交、并和补等运算，在此不加详述。

2.3 基于夹角余弦的GFSS相似性度量

相似性度量是一个用于确定两个对象间相似程度的重要工具。本文在以往研究的基础上，针对GFSS自身特点，提出基于夹角余弦的GFSS相似性度量算法。由第二节的讨论，可得Fμ的一般矩阵表达形式：

(2.1)

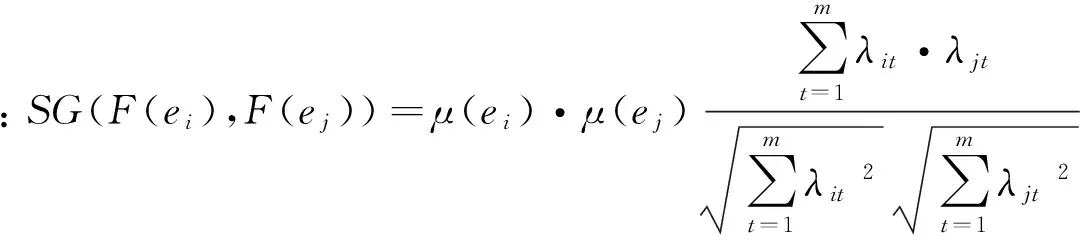
(2.2)

其中λit为矩阵Fμ中的元素，且0≤λit≤1，i,j=1,2,…,n,t=1,2,…m。同样地，可知SG(F(ei),F(ej))满足如下性质：

(1)0≤SG(F(ei),F(ej))≤1；

(2)SG(F(ei),F(ej))=SG(F(ej),F(ei))；

(3)SG(F(ei),F(ej))=μ(ei)·μ(ej)成立,当且仅当F(ei)=F(ej)成立。

以上性质的证明可由(2.2)式推导可得。可见，本文提出的基于夹角余弦的GFSS相似性度量方法充分考虑了GFSS中的所有有效信息，满足相似性度量的基本原理和性质，在组合模型最优权系数的确定过程中具有重要意义。

3 云计算环境下基于GFSS的资源需求组合预测模型

3.1 基于GFSS组合预测模型构建

为了解决组合预测模型权重的确定问题，本文将GFSS引入到组合模型的构建当中，然后利用GFSS相似性度量方法和单项预测模型预测精度求解组合预测模型的权重系数，获得最优组合预测模型。而由各单项模型转化到其GFSS形式的关键是如何准确地表达预测值与实际值之间的关系，从而准确反映出单项预测模型的预测性能，即如何通过单项预测值求得GFSS中的λ和μ值。其中λ值用于获得每个预测点的优劣，而μ则需要利用某个单项模型的所有预测值提供的信息对该模型整体的预测效果做出定量评估，本文给出以下定义。

定义3.1：令λit和μi分别为广义模糊软集合(F,X)中的元素，定义：

(3.1)

(3.2)

其中，λit即为第i个预测模型在t时刻的预测精度，而由基于距离概念定义的μi构成的隶属度向量(μ1,μ2,…,μn)用于评估第i个预测模型的总体预测性能。

由定义3.1所求得的λ和μ值能准确反映单项模型的预测性能，又能将其合理的转化到GFSS形式，从而可以建立个单项模型关于时间序列点的广义模糊软集合Fμ：

其一般的表达形式如表1所示。

由表1，利用公式(2.2)计算以上每一个Fμ(xi)与Fμ(yt)之间的相似度SG(xi,yt)，在此基础上可得每个单项预测模型在组合模型中的权重ωi：

(3.3)表1 本文构建的GFSS表格形式

基于以上论述，给出基于广义模糊软集合的组合预测算法流程：

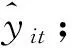
步骤2：利用公式(3.1)和(3.2)计算λit及μi，构建广义模糊软集合(F,X)；

步骤3：利用GFSS相似性度量公式(2.2)计算每个单项模型预测值与实际时间序列值的GFSS相似度SG(Fμ(xi),Fμ(yt))；

步骤4：利用公式(3.3)获得每个单项模型的权重ωi；

3.2 单项预测模型选择及模型构建

在云计算环境下，业务需求呈现多元化，海量数据存储与分析、科学工程计算、互联网及无线移动终端应用等都将是其服务的内容。用户把与各自业务相关的应用程序放置在运营商的服务器上，每个应用程序又由多个组件构成，各个组件又分别运行在不同的虚拟机上，这些因素导使云计算资源需求具有很强的非线性性和动态性，从而给预测本身以及单项预测模型的合理选择带来了困难，因此，需要对云计算资源负荷特征有清晰的了解才能做到合理、准确预测。

Benson等[22]和Tan Jian等[23]对目前云计算平台上运行的各类应用作了了分类，并对工作流特性进行了统计分析，揭示了多租户环境下CPU和内存等虚拟化资源的需求特征。从分析可得，云计算的资源负荷时间序列具有一定的模式，主要表现出以下几个特性：(1)周期性。主要表现在负荷曲线会依据人类生产、生活规律，总体上会表现出相应的周期性特点，如日和周的循环时间效应。(2)应用相关性。即云计算负荷会随着运行在该平台上应用的不同而在一定时间范围内展现出特定的需求趋势，如计算密集型应用会对CPU资源产生大量需求导致其负荷上升，数据密集型应用(如MapReduce，搜索等)会占用大量I/O及存储资源从而导致两者需求的增加，而在线游戏、视频等服务同时会对CPU和内存提出大批资源请求，这些应用会明显地影响其负荷。(3)随机性。目前云计算提供的计价服务主要包括两种形式：预定(Reservation)和按需供应(On-Demand)[24]，而资源需求的随机性不仅来自于按需供应这一块，预定资源同样也会产生随机性需求，当预定的资源不足时，增加的资源需求便要按需供应，这样就更加突显了云计算资源需求的复杂性和不确定性。基于以上分析可知，选择合适的单项模型对于预测性能的提升有着重要作用。

首先，针对云计算资源需求过程中出现的强非线性，高不确定性和时变特性，本文选用自适应神经模糊推理系统(Adaptive Neuro-Fuzzy Inference System，ANFIS)对资源需求进行预测。ANFIS是一种多层前馈神经网络，利用神经网络学习算法和模糊推理规则将输入空间映射到输出空间。由于其能将模糊推理系统的语言处理能力有效地结合到自适应神经网络系统的数值处理能力中，并允许从数值数据或专家知识的模糊性中提取规则，自适应地构造一个规则库，使得ANFIS具有良好的学习、模型构建和数据分类能力。下面将介绍本文基于ANFIS模型的预测步骤, 表2给出下文中要用到的主要标示, 图1给出了本文所建的ANFIS模型示意图。

步骤1：需求负荷时间序列聚类。在多用户环境下不可避免的会产生需求的动态变化，这种不确定性给预测带来诸多困难，该步骤的主要目的是从大量的历史数据集中辨识出需求负荷时间序列中隐含的主要云计算应用类型，反映出系统运行的实际情况。因此在预测前，本文用C-means算法[24]将待预测的数据集进行聚类分析，使同一子类中包含同类型的数据。对于时间序列Y(t)={y1,y2,…,yt}，定义其动态情况表达值ΔY(t)为：

ΔY(t)={yt-yt-1,yt-1-yt-2,…,y2-y1},

(3.4)表2 符号及标示

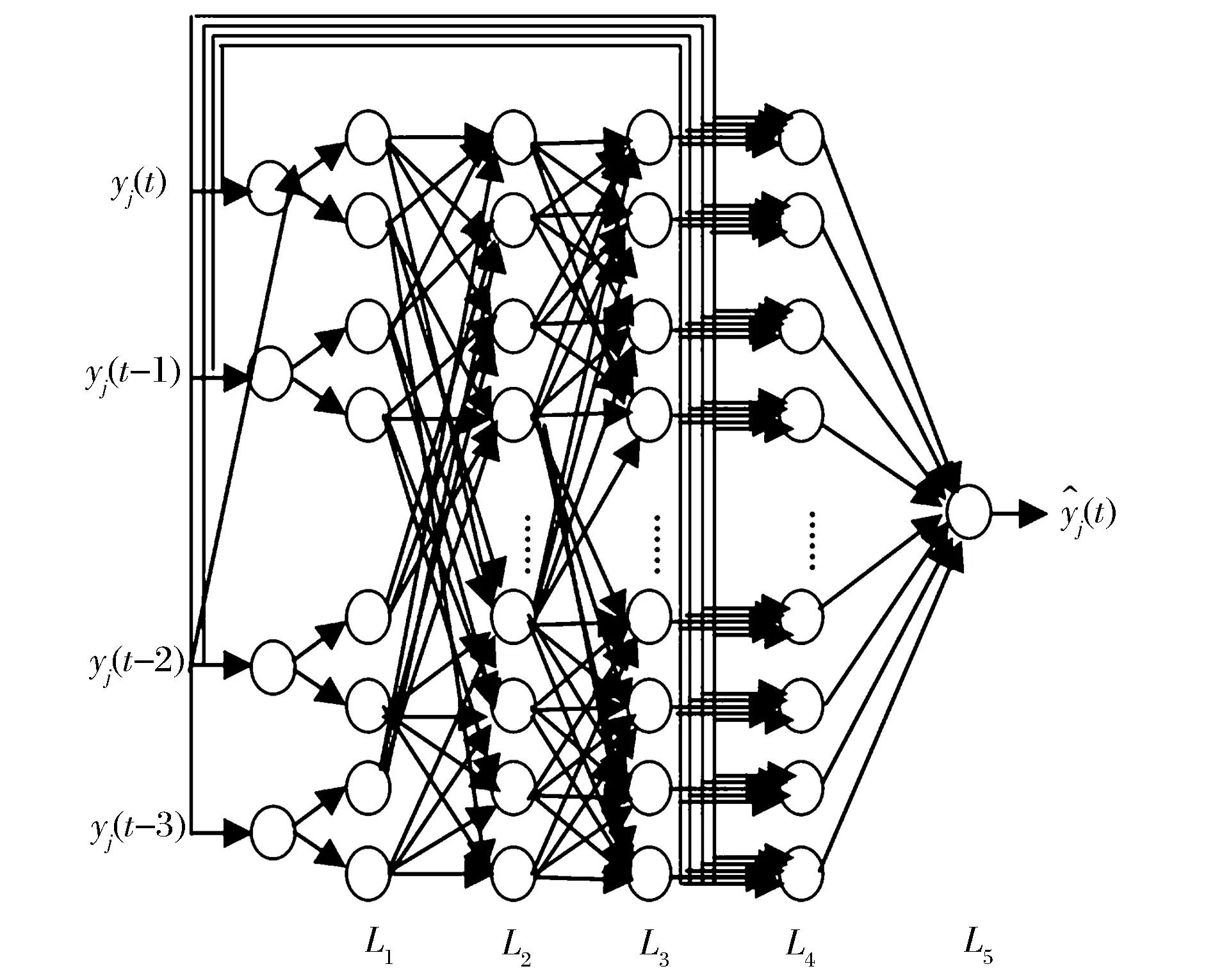
图1 ANFIS预测模型

根据动态情况表达式Δyt的值，C-means算法依据yt在某一聚类j中的隶属度μj将其划拨到特定的类中，该算法的目标函数为：

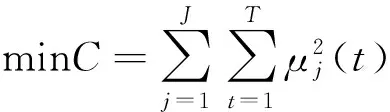
(3.5)

其中νj为第j个聚类的中心，J为聚类总个数。

步骤2：聚类间状态转移。对云计算资源需求时间序列进行聚类后，需要计算各个聚类间的状态转移概率，这一步骤的目的是为了接下来在用ANFIS获得各个聚类的预测值后，能合理地分配各预测值的比率，最终得到理想的预测结果。在此，我们用贝叶斯推理来获得所需的聚类间状态转移概率，即：

ξj,j′(t)=P(yt∈Cj|yt-1∈Cj′)

=P(yt-1∈Cj′|yt∈Cj)×P(yt∈Cj)

(3.6)

其中先验概率：

(3.7)

Nt,j为t时刻时间序列中在聚类Cj中的数据个数，N为时间序列数据总数。条件概率P(yt-1∈Cj′|yt∈Cj)的值可由LaplaceCorrection法进行估计：

(3.8)

Nt-1,j′为t-1时刻聚类Cj′中的数据个数。

步骤3：ANFIS预测。为了在保证预测准确性的同时降低计算复杂度，本文构建的基于ANFIS的云计算资源预测模型是具有四个输入{yj(t-3),yj(t-2),yj(t-1),yj(t)}的五层结构(当输入超过4个时，产生的规则数目过多，将大大增加训练和预测时间并降低预测性能)，产生RULE(24)，即16条推理规则。在输入层，根据Takagi-Sugeno模糊推理法可得：

THEN

(3.9)

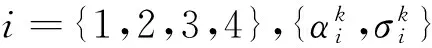
在L2层，利用上一层获得的隶属度值，用下式计算获得该层的输出值：

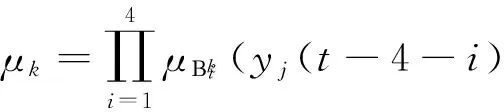
(3.10)

在L3层，计算每个节点的激励强度占所有节点总激励强度的比率：

(3.11)

在L4层，将L3层每个节点的标准化激励强度值与输入层由Takagi-Sugeno模糊推理法得到的初始输入值进行线性组合，得到第j个聚类的ANFIS预测值，公式如下：

(3.12)

在L5层，将获得的每个聚类的预测值用于计算全局预测值，以此来得到下一时刻的云计算资源需求值，利用由公式(3.6)求得的聚类间状态转移概率，以及每个聚类在t-1时刻的状态先验概率P(St-1=j′)以获得t时刻每个聚类在t时刻的状态先验概率：

(3.13)

最后获得整个数据集的ANFIS预测值：

(3.14)

接下来，针对云计算资源需求过程中体现出的周期性和趋势性特点，本文利用季节性ARIMA模型SARIMA来进行预测，它对于循环周期性时间序列数据具有优良的预测性能。如Tseng等[25]中所述,季节性ARIMA模型ARIMA(p,d,q)(P,D,Q)s的表达式为：

θp(B)Θp(BS)(1-B)d(1-BS)Dyt=wq(B)WQ(BS)at

(3.15)

其中：

wq(B)=1-ψ1B-ψ2B2-…-ψqBq

(3.16)

θp(B)=1-θ1B-θ2B2-…-θpBp

(3.17)

Θp(BS)=1-Θ1BS-Θ2B2S-…-ΘPBPS

(3.18)

WQ(BS)=1-W1BS-W2B2S-…-WQBQS

(3.19)

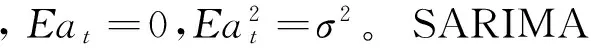
最后，在获得了由单项模型ANFIS及SARIMA预测出的未来一段时间内云计算资源需求值之后，需要计算出基于GFSS理论单项预测模型权重wANFIS和wSARIMA，构建云计算环境下的资源需求组合预测模型GFSS-ANFIS/SARIMA，流程如图2所示。

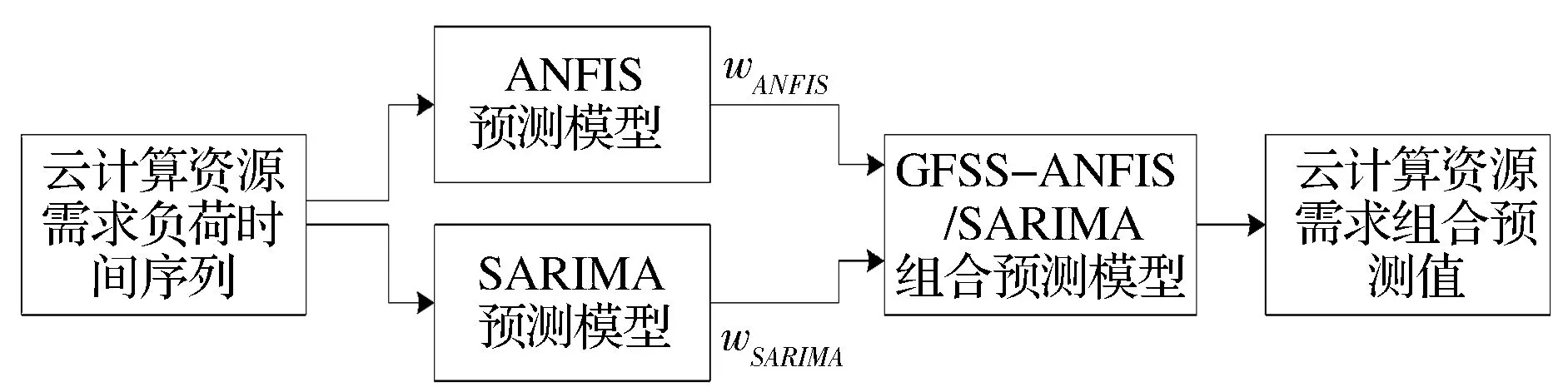
图2 基于GFSS-ANFIS/SARIMA的云计算资源需求组合预测流程图

4 实验及结果分析

本文所用实验数据来自NASA和Clarknet[26],该数据详细记录了每秒钟两个数据中心接收到的服务请求内容，在许多研究[8,27,28]中已被多次用于云计算需求预测及性能分析研究。为了综合验证本文所建组合预测模型的性能，本文在数据预处理阶段将所抽取的实验数据以10秒和60秒两个不同的粒度进行聚合，以此来生成四组数据集：NASA-10、NASA-60、Clarknet-10和Clarknet-60，每组5000个训练数据，并预测接下来的300个数据点，目的是检验GFSS-ANFIS/SARIMA组合模型在处理短期的波动性时间序列数据(NASA-10和Clarknet-10)，以及长期周期性时间序列数据(NASA-60和Clarknet-60)时，是否都表现出稳定的预测性能和准确的预测结果。本文选择以平均绝对百分比误差(MAPE)和均方根误差(RMSE)两个指标作为衡量预测性能是否优良的评价指标：

(1)MAPE：

(2)RMSE：

为了验证GFSS-ANFIS/SARIMA组合预测模型有效性，本文选取自回归移动平均(ARMA)、BP神经网络及指数平滑三个模型作为对比，其中ARMA模型的自回归项数p和模型的移动平均项数q分别设为p=2和q=1,BP神经网络的隐含层个数设置为20，指数平滑采用二次平滑，选取前300个点的平均值作为平滑初值，平滑参数α经过计算机自动识别，确定为α=0.36，此时方差最小。图3为本文所建组合预测模型GFSS-ANFIS/SARIMA的预测结果示意图，图4给出了该模型与各单项模型的预测精度比较结果。

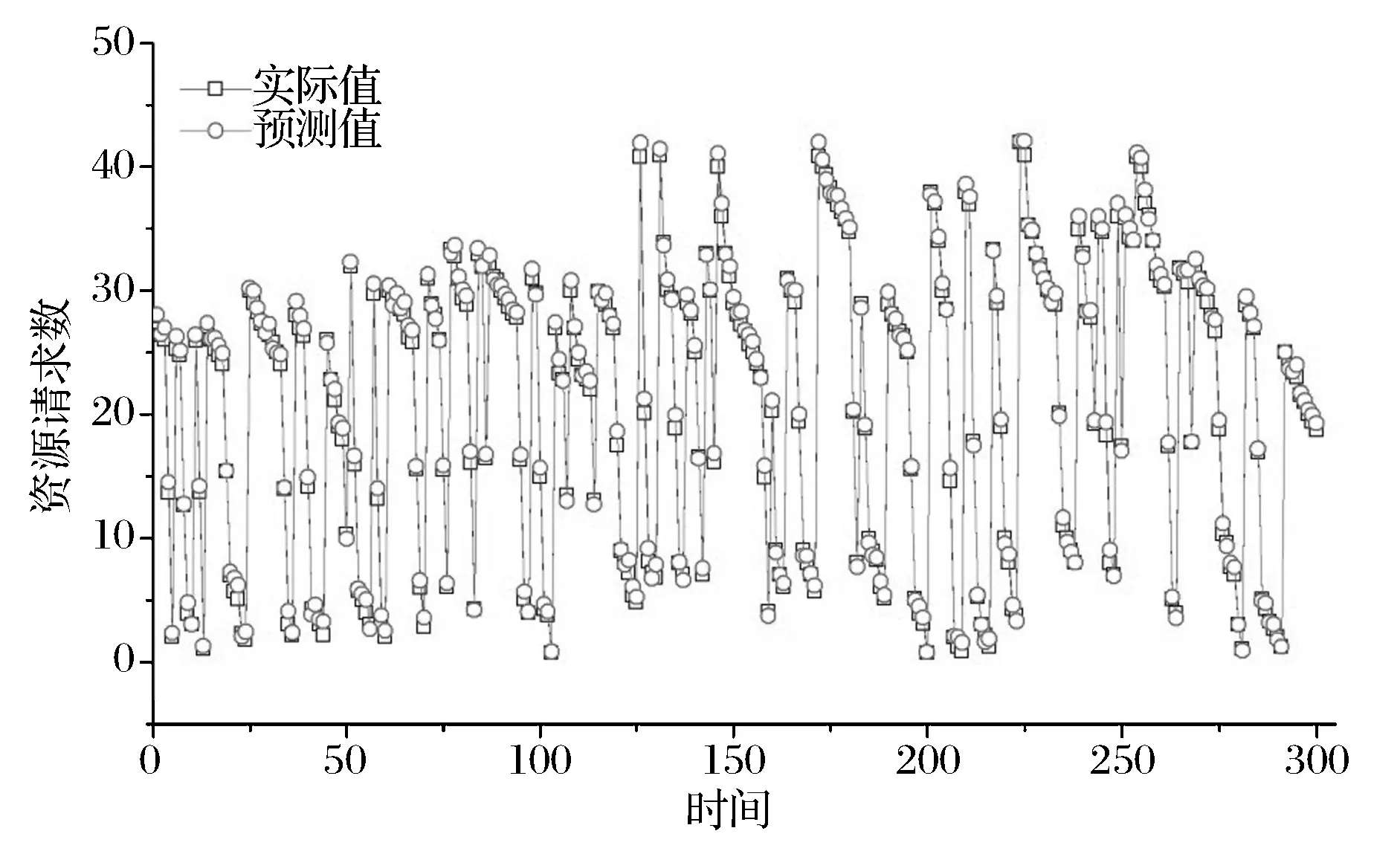
图3(a) NASA-10预测结果

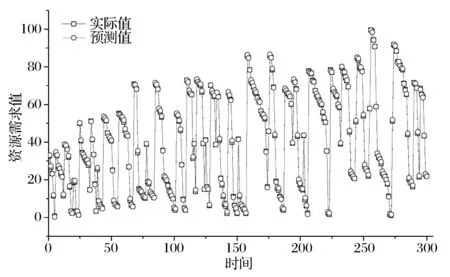
图3(b) Clarknet-10预测结果

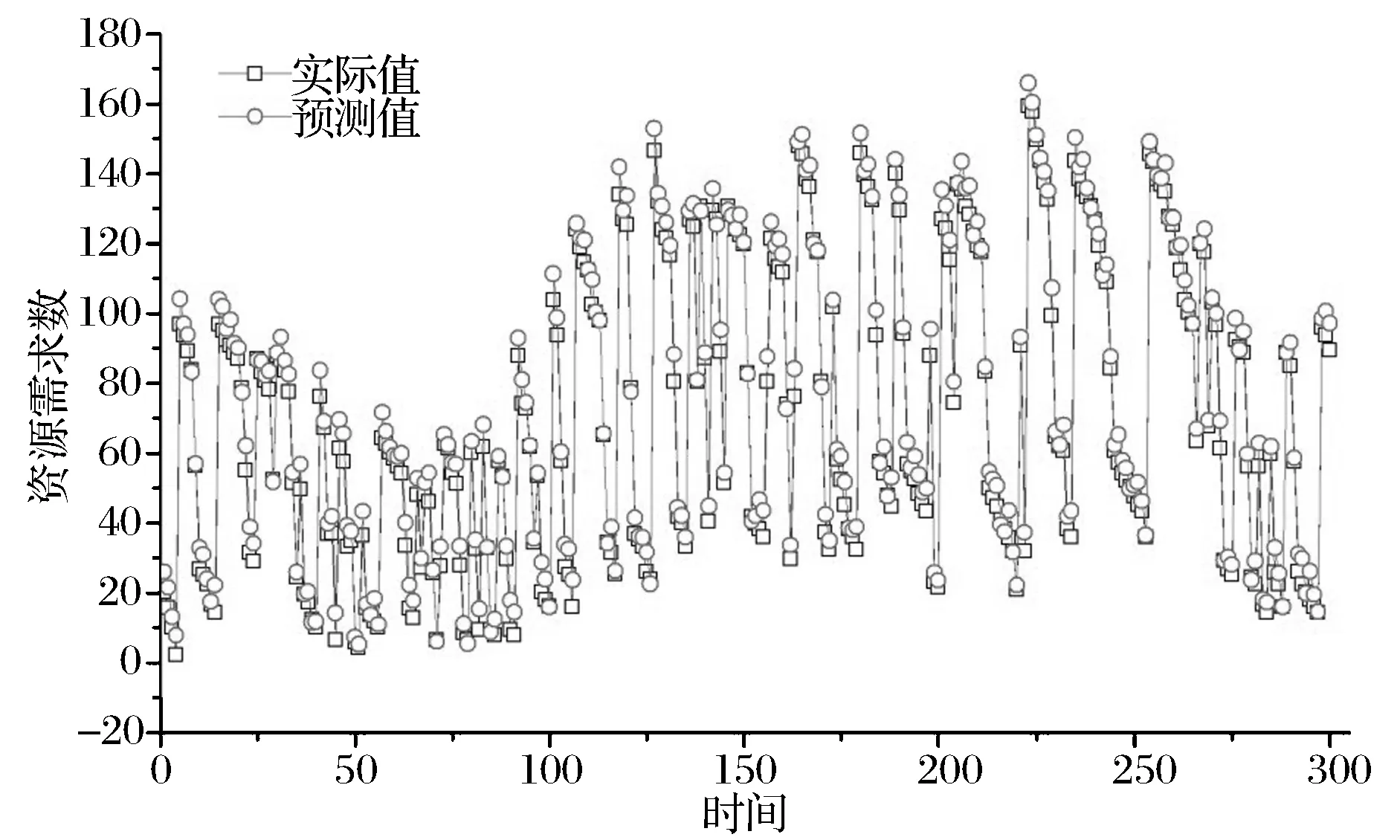
图3(c) NASA -60预测结果

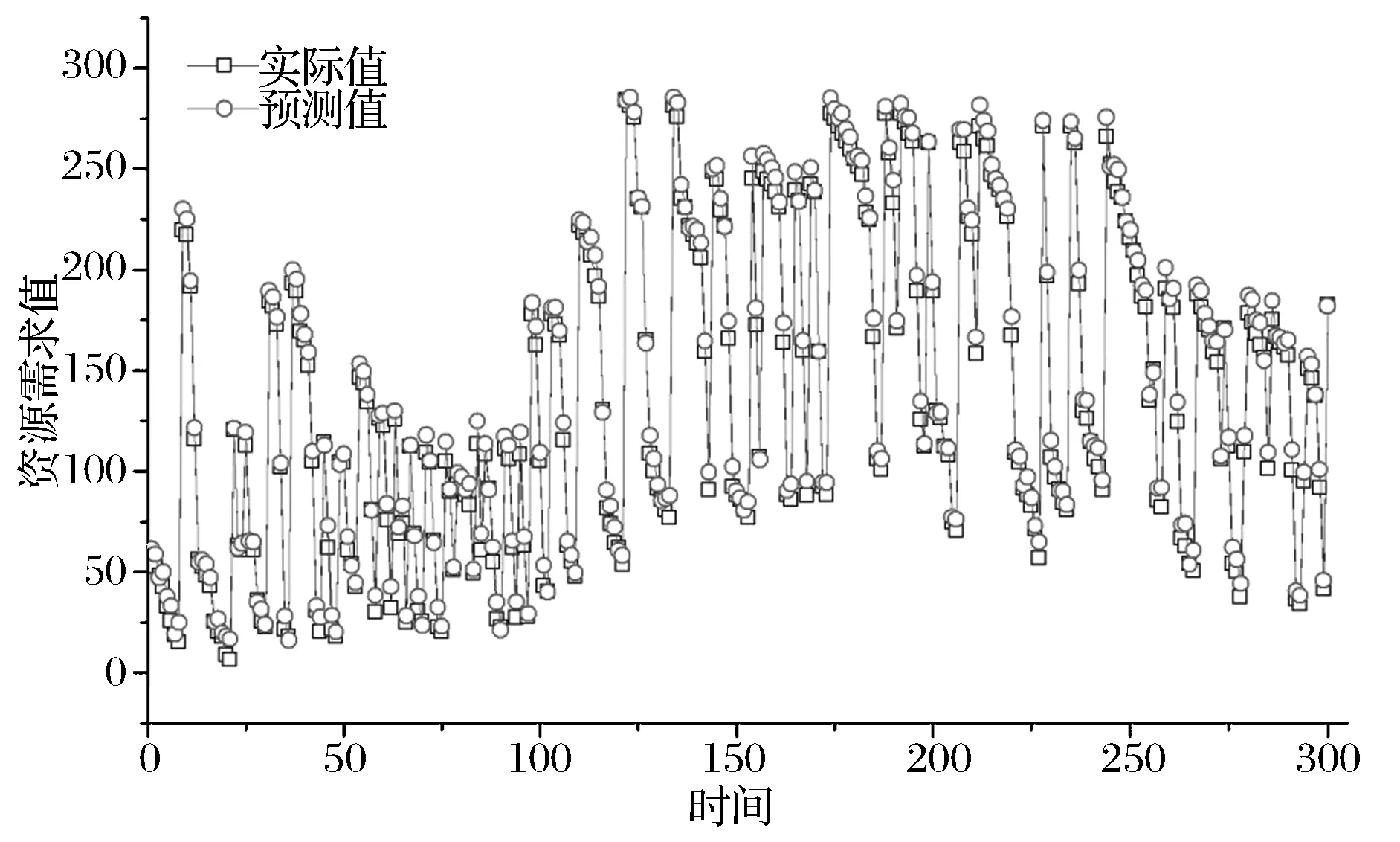
图3(d) Clarknet-60预测结果

图4 与单项模型预测结果相对误差的比较示意图

从图4可以看出，本文构建的组合模型相对于以上几个单项模型，在预测性能上有显著地提升。同时也注意到，利用Clarknet数据获得的预测精度要优于NASA，原因可能是Clarknet数据比NASA数据更有规律性，相对较平稳，也易于模型把握其总体趋势和特征，从而表现出更小的预测误差。在与传统的时间序列单项模型比较的基础上，再用本文所用的三个单项模型，构建陈华友[11]研究中的基于IOWGA算子的组合预测模型，以及XiaoZhi等[14]研究中所提的基于模糊软集合理论(FSS)的组合预测模型与本文建立的组合预测模型在预测效果上进行比较。

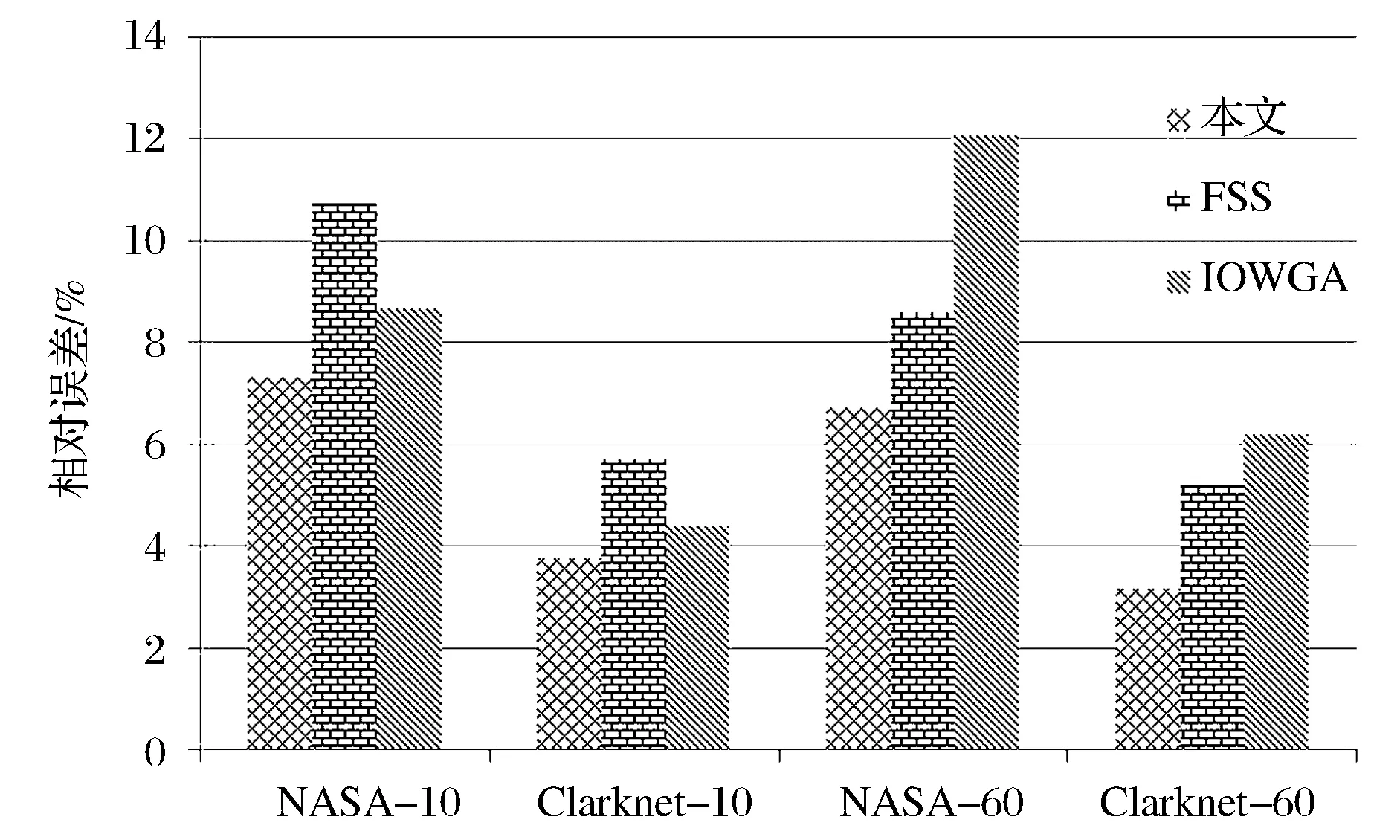
图5 与组合模型预测相对误差的比较示意图

图5为本文构建的模型与以上两个组合预测模型的预测结果比较示意图，表3给出了总的数值比较结果。

从预测结果比较中可以看到，本文所提的组合预测模型预测值与实际值在整体上最为贴近，不仅从直观上反映出该模型良好的预测性能，而且在各评价指标上也体现出较大的优势。与传统的单项时间序列预测模型相比，在预测精度和效果上都有明显的提高，而在组合预测算法时间复杂度上，本文为O[n·(m+1)]，相比于XiaoZhi等[14]研究中的O[n·m]，只用了较小的代价获就得预测精度的有效提升，而相比于陈华友[11]的时间复杂度O[n·m2]，不管在预测精度上还是时间复杂度上，本文算法都优于陈华友[11]。综上所述，本文所构建的组合预测模型在实际运用过程中能准确析取云计算负荷数据中所蕴含的信息内容，并将对数据信息内容的理解融入到模型构建及预测的过程中去，在提升预测精度的同时具有良好的非线性及动态时间序列预测性能。

5 结语

本文首先介绍了云计算资源需求预测在实现云计算资源高效管理中的作用，阐述广义模糊软集合理论相关概念，将该理论引入到组合预测模型的构建当中，提出了广义模糊软集合的相似性度量公式，并将相似性度量结果与单项模型的预测精度结合获得组合预测模型中各单项模型的最优权值，构建了基于广义模糊软集合理论、自适应神经模糊推理系统ANFIS及季节性ARIMA模型SARIMA的优化组合预测模型GFSS-ANFIS/SARIMA，并将该组合预测模型用于云计算环境下的资源需求预测，实验结果表明了该组合模型的有效性和合理性。

表3 各模型预测精度比较

[1] Bianchini R， Rajamony R. Power and energy management for server systems[J]. Computer, 2004, 37(11):68-74.

[2] Guenter B, Jain N, Williams C. Managing cost, performance, and reliability tradeoffs for energy-aware server provisioning[C].Proceedings of the 30th IEEE International Conference on Computer Communications,Shanghai,China,April 10-15,2011.

[3] Baliga J, Ayre R W A, Hinton K,et al.Green cloud computing: Balancing energy in processing, storage, and transport[J]. Proc. IEEE, 2011, 99(1):149 -167.

[4] Garg S K, Yeo C S, Anandasivam A,et al. Environment-conscious scheduling of HPC applications on distributed cloud-oriented data centers[J]. Journal of Parallel and Pistributed Computing, 2011, 71(6): 732-749.

[5] Mark C C T,Niyato D,Che-khong T. Evolutionary optimal virtual machine placement and demand forecaster for cloud computing[C].Proceedings of the 25th International Conference on Advanced Information Networking and Applications, Biopolis,Singapore,March 22-25,2011.

[6] Caron E, Desprez F, Muresan A. Forecasting for grid and cloud computing on-demand resources based on pattern matching[C]. Proceedings of the 2nd IEEE International Conference on Cloud Computing Technology and Science,Indianapolis,November 30-December 3,2010.

[7] Islam S, Keung J, Lee K, et al. Empirical prediction models for adaptive resource provisioning in the cloud[J]. Future Generation Computer Systems, 2011,28(1): 155-162.

[8] Duy T V T, Sato Y, Inoguchi, Y. Performance evaluation of a green scheduling algorithm for energy savings in cloud computing[C].Proceeding of International Symposium on Parallel Distributed Processing Workshops and Phd Forum IPDPSW,Atlanta,GA,April 19-23,2010.

[9] Dickinson J P. Some comments on the combination of forecasts[J]. Operational Research Quarterly, 1975,26(1):205-210.

[10] Bates J M, Granger C W J. The combination of forecasts[J]. Operations Research Quarterly, 1969, 20(4): 415-468.

[11] 陈华友,盛昭瀚.一类基于IOWGA算子的组合预测新方法[J].管理工程学报,2005,19(4):36-39.

[12] 孙李红,沈继红.基于相关系数的加权几何平均组合预测模型的性质[J].系统工程理论与实践,2009,(9): 84-91.

[13] 李美娟,陈国宏,林志炳.基于漂移度的组合预测方法研究[J].中国管理科学,2011,19(3):111-117.

[14] Xiao Zhi, Gong Ke, Zou Yan. A combined forecasting approach based on fuzzy soft sets[J]. Journal of computational and Applied Mathematics, 2009,228(1): 326-333.

[15] Molodtsov D. Soft set theory-first results[J]. Computers & Mathematics with Application, 1999,37(4):19-31.

[16] Maji P K, Roy A R, Biswas R. An application of soft sets in a decision making problem[J]. Computers & Mathematics with Application, 2002,44(8):1077-083.

[17] 孙智勇,刘星.模糊软集合理论在税收组合预测中的应用[J].系统工程理论与实践,2011,31(5): 936-943.

[18] Majumdar P, Samanta S K. Generalized fuzzy soft sets[J]. Computers & Mathematics with Application, 2010, 59 (4): 1425-1432.

[19] Xiao Zhi, Yang Xianglei,Niu Qing,et al. A new evaluation method based on D-S generalized fuzzy soft sets and its application in medical diagnosis problem[J]. Applied Mathematical Modelling,2012, 36(10): 4592-4604.

[20] Maji P K, Biswas R, Poy A R.Intuitionistic fuzzy solf sets[J]. Journal of Fuzzy Mathematics,2001, 9(3): 677-692.

[21] Bustince H, Barrenechea E, Pagola M. Image thresholding using restricted equivalence functions and maximizing the measures of similarity[J]. Fuzzy Sets and Systems, 2007, 158(5): 496-516.

[22] Benson T, Akella A, Maltz D A. Network traffic characteristics of data centers in the wild[C].Proceedings of the 10th ACM SIGCOMM conference on Internet measurement,Melbourne,Australia,November 1-3,201 1-3,2010.

[23] Tan Jian, Dube P, Meng Xiaoqiao, et al. Exploiting resource usage patterns for better utilization prediction[C].Proceedings of the 31st International Conference on Distributed Computing Systems Workshops (ICDCSW’11), Minneapolis,Minnesota,USA,June 20-24,2011.

[24] Bezdek J, Pal S. Fuzzy models for pattern recognition[M].New Jersey,USA: IEEE Press, 1992.

[25] Tseng F M, Tzeng G H. A fuzzy seasonal ARIMA model for forecasting[J]. Fuzzy Sets and Systems, 2002, 126(3): 367-376.

[26] Traces in the Internet traffic archive[DB/OL]. http://ita.ee.lbl.gov/html/traces.html.

[27] Mehta A, Menaria M,Dangi S,et al. Envergy conservation in cloud infrastructures[C]. Prceedings of 5th Annual IEEE International Systems Conference, Montreal,Canada,April, 4-11,2011.

[28] Prevost J J, Nagothu K M,Kelley B,et al. Prediction of cloud data center networks loads using stochastic and neural models[C].Proceeding of 6th International Conference on System of Systems Engineering, Albuquerque,USA,dune 27-30,2011.

Research on Generalized Fuzzy Soft Sets Theory based Combined Model for Demanded Cloud Computing Resource Prediction

XU Da-yu1,2, YANG Shan-lin2, LUO He2

(1.Zhejiang A&F University,Zhejiang Provincial Key Laboratory of Forestry Intelligent Monitoring and Information Technology Research,Hangzhou 311300,China;2.HeFei University of Technology, Key Laboratory of Process Optimization and Intelligent Decision-making,Ministry of Education, HeFei 230009, China)

In order to realize high scalability, flexibility and cost-effectiveness, cloud computing platforms need to be able to quickly plan and provision resources. To this end, it calls for mechanisms to predict demanded resource effectively. Therefore, resource prediction is a crucial issue for efficient resource utilization in dynamic cloud computing environment. In this paper, the basic concept of generalized fuzzy soft sets is introduced, and a novel angle cosine is proposed based similarity measurement of generalized fuzzy soft sets. Then the similarity measurement result and the prediction accuracy from Adaptive Neuro-Fuzzy Inference System and Seasonal ARIMA model are adopted to obtain the weights of combined prediction model. On this basis，the generalized fuzzy soft sets theory based on the combination of forecasting model GFSS-ANFIS/SARIMA is constrncted. Finally, this model is explorted to predict the demanded resource in cloud computing. The experimental results show that the proposed model can significantly improve the prediction accuracy with high prediction performance. Efficient decision support for resource scheduling and allocation in cloud computing can be provided by the proposed method.

cloud computing; generalized fuzzy soft sets; combined prediction; similarity measurement; adaptive neuro-fuzzy inference system

1003-207(2015)05-0056-09

10.16381/j.cnki.issn1003-207x.2015.05.008

2012-11-20；

2013-06-17

国家自然科学基金资助项目(71131002, 71071045)；浙江农林大学校科研发展基金人才启动项目(2014FR082)

徐达宇(1985-)，男(汉族)，浙江杭州人，浙江农林大学信息工程学院讲师,研究方向：预测理论与方法、云计算.

TP391

A