拓展映射法求非线性偏微分方程的新解

何红生

（集美大学理学院，福建厦门 361021）

拓展映射法求非线性偏微分方程的新解

何红生

（集美大学理学院，福建厦门 361021）

构建了一种拓展的映射法（F展开法）求解某些非线性偏微分方程（PDEs）的精确解.研究表明，该拓展的映射法不仅能够求得方程的Jacobi椭圆函数的整数幂指数形式解，而且能够求得非线性方程的分数幂指数形式（1＋δf2（ξ））1／2的Jacobi椭圆函数解.

拓展的F展开法；Jacobi椭圆函数；耦合Klein-Gordon-Schrödinger方程

0 引言

非线性方程是解释大多数非线性物理现象的重要方法，所以，求解非线性物理方程的精确解是很有意义的研究课题.在过去的几十年里，研究者们发展了大量有效的方法来求解非线性方程的精确解，比如：反散射法［1］、Backlund变换［2］、Darboux变换［3］、截断Painleve展开法［4］、Hirota双线性法［5］、正弦-余弦法［6］、双曲正切函数法［7］、齐次平衡法［8-9］，等等.众所周知，椭圆函数（如Jacobi椭圆函数和Weierstrass椭圆函数等）与非线性偏微分方程有着密切的关系［10-12］.而且，研究［13-15］表明，很多非线性方程有椭圆函数解.近年来逐渐发展起来的映射展开法［16-17］可以求得Jacobi椭圆函数解，并且在极限情况下可分别求得方程的孤立波和三角函数周期解.本文将构建一种拓展的映射展开法，并用于求解耦合的Klein-Gordon-Schrödinger（K-G-S）方程.

1 拓展的映射展开法

考虑一非线性偏微分方程形式如下：

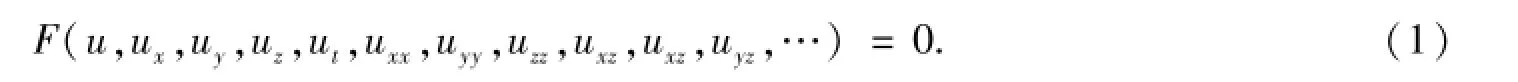
首先假定方程以下形式的行波解：

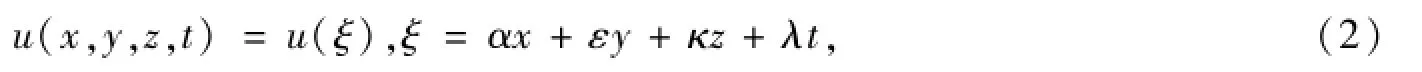
则方程（1）变为非线性常微分方程：

假设方程（3）有以下形式的解：

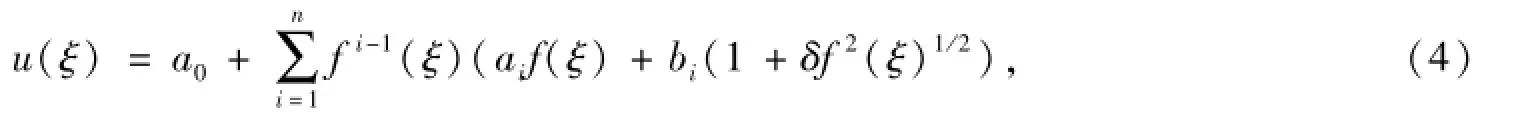
其中：a0，ai，bi，δ（δ≠0）为待定的系数；n为由方程的最高阶线性导数项和最高阶非线性项决定的齐次平衡数；f（ξ）满足以下形式的Jacobi椭圆方程：

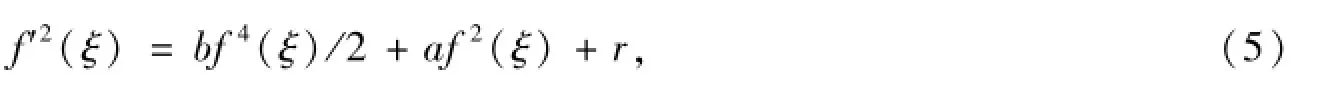
其中：a，b，r是参数，并且不同的系数组合，f（ξ）对应着不同的Jacobi椭圆函数.

考虑方程（5），把式（4）代入到方程（3），则方程（3）的左边转化为有关f（ξ）的多项式.并且令多项式的系数为零，这样得到有关a0，ai，bi，α，ε，κ，λ和δ的方程组.求解这方程组确定系数，并且选择不同的参数（a，b，r），将得到方程（1）的不同形式的椭圆函数解，其中包括Jacobi椭圆函数的整数幂指数形式解和Jacobi椭圆函数的分数幂指数形式解.此外，考虑椭圆函数的模数m→1或者m→0时，椭圆函数分别退化成双曲函数和三角函数，这样就可以同时得到有关方程的孤立波解和三角函数周期解.

2 拓展的映射法的应用

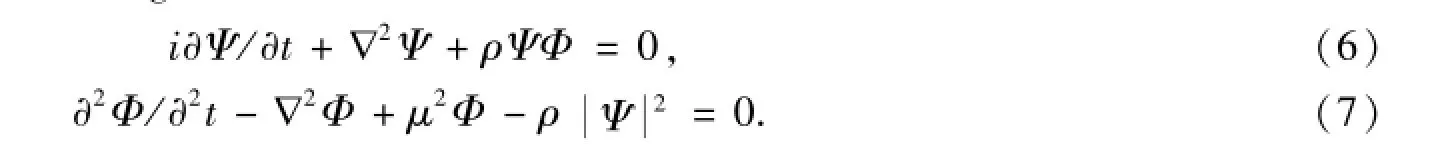
该方程组描述保守的标量核子与中性标量介子内相互作用的系统.其中：Ψ表示核子复标量场；Φ表示介质标量场；实系数μ和ρ分别描述介子的质量和耦合常数，拉普拉斯算符表示为∇2＝∂2／∂x2＋∂2／∂y2＋∂2／∂z2.

为了简便起见，只求方程（6）、（7）的行波解，作如下变换：

其中：ξ＝x＋cy＋dz＋et；η＝px＋qy＋Rz＋st.这样方程（6）、（7）变为如下的常微分方程：

耦合的Klein-Gordon-Schrödinger如下：

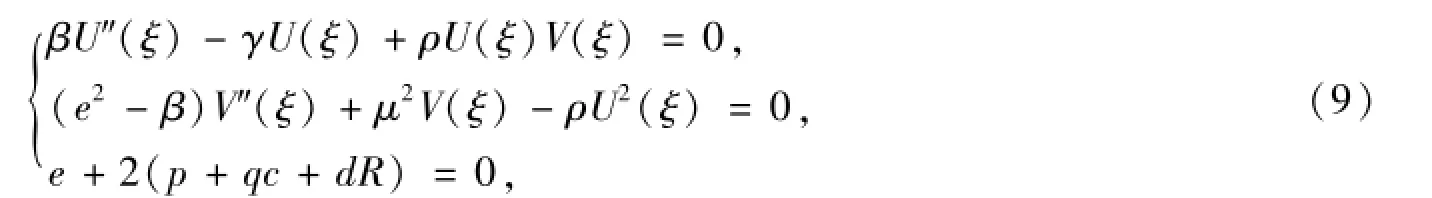
其中：β＝1＋c2＋d2；γ＝s＋p2＋q2＋R2；s为待定的常数.

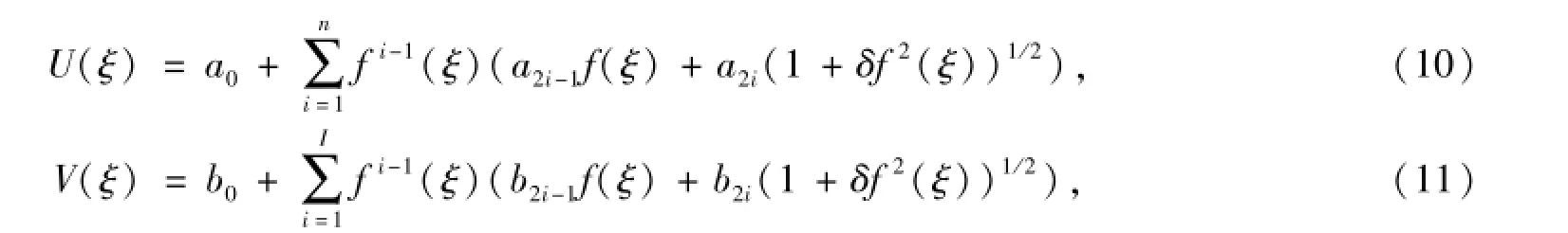
根据拓展的映射法，作如下假设：n和I分别由最高阶导数项U″（ξ）和V″（ξ）与非线性项U（ξ）V（ξ）和U2（ξ）平衡确定.容易确定可得n＝I＝2，因此方程（9）的形式解表示为：

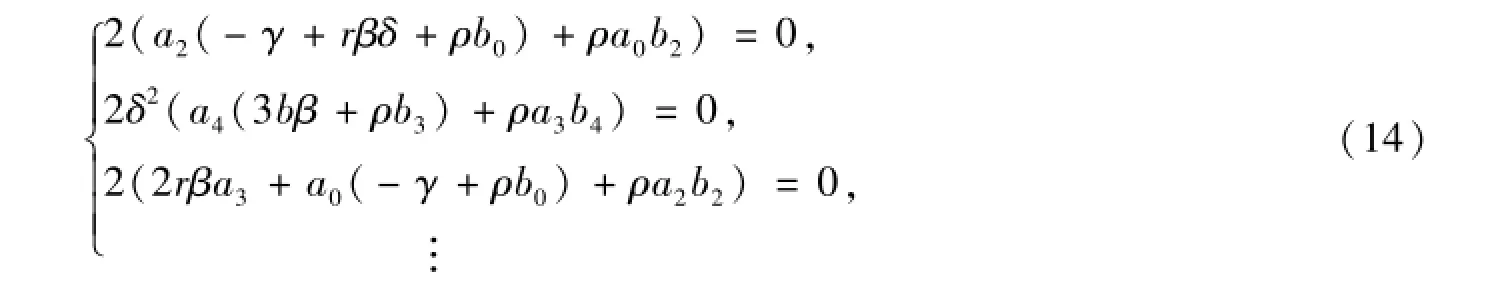
3 结论

本文主要构建了拓展的映射展开法，并用于求解耦合K-G-S方程.研究结果表明，运用该方法不仅可以得到整数的幂指数形式的Jacobi椭圆函数解，同时还可以得到形如（1＋δf2（ξ））1／2的分数幂指数形式的Jacobi椭圆函数解.

［1］GARDNER CS，GREENE JM，KRUSKAl M D，et al.Method for solving the Korteweg-de Vries equation［J］.Phys Rev Lett，1967，19：1095-1097.

［2］WAHLQUIST H D，ESTABROOK F B.Bäcklund transformation for solutions of the Korteweg-de Vries equation［J］. Phys Rev lett，1973，31：1386-1390.

［3］MATVEEV V A，SALLEM A.Darboux transformations and solitons［M］.Berlin：Springer-Verlag，1991.

［4］CONTE R，MUSETTE M.Variable separation and derivative dependent functional separable solutions to generalized KdV equations［J］.JPhys Math，1990，23：3923.

［5］HIROTA R，SATSUMA J.Soliton solutions of a coupled Korteweg-de Vries equation［J］.Phys Lett A，1981，85：407-408.

［6］FAN E G，Extended tanh-function method and its applications to nonlinear equations［J］.Phys Lett A，2000，277：212-218.

［7］WANGM L.Solitary wave solutions for variant Boussinesg equations［J］.Phys Lett A，1995，199：169-172.

［8］YANG L，LIU JB，YANG K Q.Exact solutions of nonlinear PDE，nonlinear transformations and reduction of nonlinear PDE to a quadrature［J］.Phys Lett A，2001，278：267-270.

［9］WANGM L，LIX Z.Simplified homogeneous balancemethod and itsapplications to theWhitham-Broer-Kaupmodel equations［J］.Journal of Applied Mathematics and Physics，2014（2）：823-827.

［10］BOWMAN F.Introduction to elliptic functions with applications［M］.London：London University，1959.

［11］PATRICK D V.Elliptic function and elliptic curves［M］.Cambridge：Cambridge University Press，1973.

［12］CHAMDRASEKHARAN K.Elliptic functions［M］.Berlin：Springer-Verlag，1985.

［13］PORUBOV A V，VELARDE M G.Amplification of nonlinear strain waves in solids［J］.JMath Phys，1999，40：884.

［14］LIUSK FUZT LIUSD.The periodic solutions for adass of coupled nonlinear klein-Gordon eqations［J］.Phys Lett A，2004，323：415-420.

［15］ZHOU Y B，WANGM L，WANG Y M.Periodic wave solutions to a coupled KdV equations with variable coefficients［J］.Phys Lett A，2003，308：31-36.

［16］LIU JB，YANG L，YANG K Q.New Jacobi elliptic function expansion and exact solutions of nonlinear PDE［J］. Chaos Solitons＆Fractals，2004，22：111-121.

［17］YOMBA EMMANUEL.Exact soliton solutions to a new coupled integrable short light-pulse system［J］.Chaos Solitons＆Fractals，2004，21：209-229.

（责任编辑 马建华 英文审校 黄振坤）

New Solutions for Nonlinear Partial Differential Equations Using the Extended M apping M ethod

HE Hong-sheng
（School of Science，Jimei University，Xiamen 361021，China）

The extended F-expansion（or mapping）method is presented to construct exact solutions to some nonlinear partial differential equations（PDEs）.Itwas shown that not only integer exponential Jacobielliptic function solutions，but also fractional exponential combined Jacobi elliptic function of the form（1＋δf2（ξ））1／2solutionswere obtained.

extended F-expansion method；Jacobi elliptic functions；coupled Klein-Gordon-Schrödinger equations

O 411.1

A

1007-7405（2015）05-0387-05

2014-09-12

2014-10-28

福建省自然科学基金资助项目（2007J0202）；集美大学科研启动基金项目（C60705）

何红生（1977—），男，讲师，博士，主要从事理论物理及数理方程的研究.