基于因子分析和DEA的高职院校效率评价——以福建省为例

黄焕宗

(黎明职业大学公共教学部，福建泉州 362000)

0 引言

澳大利亚新英格兰大学(UNE)在一项针对该国36所高校的管理效率研究中，构建了管理人员支出、其他管理成本、学生总数、教职工总数的双投入—双产出DEA模型，结果证实了UNE管理层规模相较于其他大学更大的猜测［1］;彭江(2004)从影响高等教育管理的“行政力量”、“市场力量”及“学术力量”出发，详细分析了高校存在的行政失灵、校内市场失灵和学术失灵现象，研究提出克服学校管理“失灵”问题的出路之一是社会经营改革［2］;谢南斌，田金信(2008)采用相对效率评价中的AHP与DEA相结合的两阶段方法，评价了高职教育的相对效率［3］。这些研究为丰富我国高等教育效率研究理论提供了宝贵的参考。然而，由于DEA对投入产出指标数量的限制和高职效率评估指标体系繁多间的矛盾以及投入产出指标之间可能存在强线性关系，在运行DEA分析之前用适当的方法整理指标体系尤为重要。本文采用降维思想的因子分析和DEA相结合的方法对福建省高职院校效率情况进行研究。

1 研究模型

1.1 因子分析

因子分析是一种降维、简化数据的技术。它通过研究众多变量之间的内部依赖关系，探求观测数据中的基本结构，并用少数几个“抽象”的变量在众多指标中获取因子之间的联系。这几个抽象的变量包含了原来众多变量之间的联系信息，对原始变量进行了归队和概括，因而被命名为“因子”。原始变量也从可观测的显在变量被归纳为不可观测的少数几个潜在变量，进而达到降维目的。每一个变量都可以表示成公共因子的线性函数与特殊因子之和，即:

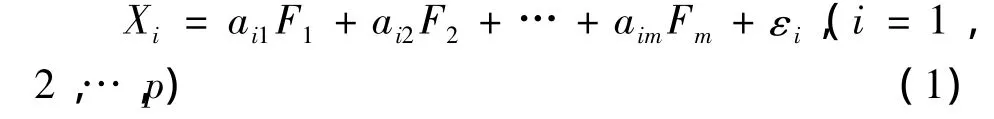
公式(1)中的 F1，F2，…，Fm称为公共因子，εi称为Xi的特殊因子。该模型可用矩阵表示为:

称为因子载荷矩阵，其组成元素aij表示的是公共因子Fj所包含的原始变量Xi的信息权重。

1.2 数据包络分析(DEA)

数据包络分析方法(DEA)是一种以相对概念为基础，主要采用数学规划方法，从投入和产出的角度去评价决策单元的有效性和部门间的相对有效性(因此被称为DEA有效)。该方法即CCR模型，数学表述如公式(3)所示:

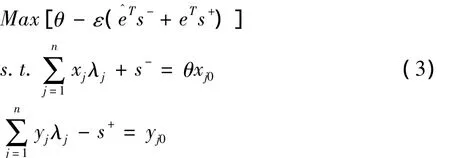
其中，λj≥ 0;j=1，2，…，n;s-为松弛变量;s+为剩余变量;e^和e分别是分量为1的m维、s维列向量;ε为非阿基米德无穷小量(比任何大于零的量都要小的量)。如果θ0＜1，则称为第j0决策单元为DEA无效;如果θ0=1，则称为第j0决策单元为弱 DEA 有效;如果 θ0=1，s-=0，s+=0，则称为第j0决策单元为DEA有效。判断决策单元的有效性，就是判断其效率值是否位于效率前沿面上。

2 实证研究

2.1 指标体系的建立

高职教育的投入指标跟一般高等教育一样，包括了人力、物力、财力三个方面的投入。考虑到高职教育培养目标与一般本科教育的区别，在人力投入方面除了对教职工职称、学历等方面的关注外，还应该着重关注教职工的技能，即“双师素质”情况。物力方面，主要由场地、教学和实验设施等存量资产构成，对高职教育而言，跟实训相关的设施和设备构成了主要的物力投入指标。财力指标跟一般本科教育大同小异。对高职教育的效率评价和分析，由于受到评标指标模糊的影响，研究成果相对较少。金晶比较分析了我国和英国的高职教育评价体系，并从培养“技术技能型”人才要求入手，建立了评价指标体系［4］。本文参考了该体系，在考虑资料可获得性前提下选取了全日制在校生数(人)、招生专业数(个)、生均校舍面积(平方米)、图书馆规模(万册)、近五年国家级教改建设项目数(项)、实训实验设备价值(万元)等指标来衡量物力和财力的投入情况。在人力投入上，则是选取了专任教师双师素质比例、专任教师高级职称比例等指标。在产出指标方面，根据高职教育与普通本科教育培养目标的不同，本文采用了省级以上科研项目立项数(个)、大型企业合作数(家)、年度社会服务收入(万元)、毕业生数(人)。以上指标全面和系统地测度了高职教育的投入和产出情况，但考虑到指标数量较大，而DEA的有效运行要求决策单位的数量最好达到投入产出指标数量的2倍以上，因而有必要进行适当的降维处理。

本文选取了2005年以来福建省获评为“国家示范性高职院校”、“福建省示范性高职院校”的11所高职院校作为研究对象，数据来源为《福建教育简明资料2013》和《2013年度福建省普通高等学校内涵建设数据汇总》。

2.2 量化分析及讨论

2.2.1 因子分析

社会经济统计软件SPSS20.0运算的结果显示，投入指标之间的相关性较强，指标的相关系数矩阵R显示，数据适合进行因子分析。为进一步检验因子分析的科学性，进行了KMO检验和Bartlett检验，Kaiser-Meyer-Olkin值为 0.726，p值为0，这两个值都位于适合的区间内，因子分析是必要和合理的。因子的方差贡献分析显示，前两个因子的累计贡献率达到90.386%，其特征值明显大于其他因子的特征值，且相关性明显［5］，说明了8个投入指标之间存在高度的信息重叠，经过因子分析被整合为两个因素。为研究方便，本文把两个因素命名为基础物质投入因子和实训能力投入因子。这两个因子在8个原始投入指标的影响权重可表示为成分得分系数阵F*，同时，每所高职院校的投入指标也被表示成关于矩阵F*的线性多项式［6］，该多项式计算的结果A*就是每所学校的新投入指标值。这组新指标值将进行DEA分析并与未进行因子分析的原始指标计算结果进行比较。产出指标的先验结果显示，Kaiser-Meyer-Olkin值为 0.34，p值为 0.016。这个结果表明产出指标之间的线性相关性不强，不需要进行因子分析。

2.2.2 DEA技术效率比较分析

在高职院校产出生产函数未知前提下［7］，本文将进行因子分析前后的投入产出指标分别带入DEA模型进行计算，其技术效率值见表1，因子分析前的数据显示，有5所高职院校的技术效率值达到1的最高分值，无论是从评价的方便性还是数据的精细性而言，这一结论都有待改善。而因子分析后技术效率达到1的院校只有3所，大大弥补了之前方法的缺陷。

2.2.3 DEA 效率分析

根据DEA技术效率值的大小可以对研究对象进行技术效率排序。因子分析前后的DEA分析所得效率排序也发生了明显的变动(见表2)，这一变动足以引起高职效率评价部门和学校的重视。使用因子分析降维之前，学校JT和ZZ的技术效率值都是1，说明两所学校的资源投入效率在原有指标体系下较高。但是降维去线性重叠后重新进行DEA分析，这两所学校的技术排行从第一分别滑落到第六和第七，甚至排行比本来靠后的WJ和SD都低。究其原因主要是投入指标降维的影响。降维之前的投入指标之间存在较为严重的信息重叠现象，某几所学院由于在某类指标的投入上占据优势，因而这类指标的数量如果较多，那么这些学校的技术效率将明显占据优势，而原始指标的降维整合无疑使这些学校在这几类指标上的优势明显降低。事实表明，学校JT和ZZ都是老牌高职名校，这几年在国家示范性建设的带动下，硬件设施得到巨大改善，因子1代表的是基础物质投入因素，恰好印证了分析结果。

学校LM、LY和QY在因子分析前后的技术效率排行保持不变，说明了这些学校在因子1和因子2的投入较为均衡，即使经过了因子的降维重组，其投入因素扔保持不变。

表1 因子分析前后DEA技术效率值对照表

表2 因子分析前后DEA技术效率排序对照表

学校XX虽然也获得国家示范性院校荣誉及配套基础投入，但由于该校相对于其他院校而言是新升格学校，基础投入转化为相对应产出需要一定时间。学校SY是专业性较强的高职院校，其DEA技术效率始终靠后，究其原因，与该校是经管类学校，而当下产出统计口径较为综合，涵盖了社会服务的各方面有关。

3 结论

DEA方法作为技术效率分析的有效方法在高校效率评价上有着广泛的应用，其优点之一在于投入产出指标的无量纲限制［8］。然而该方法的缺点也是存在的，评价单元数量和评价指标数量之间的相对关系以及评价指标之间的线性关系都会影响DEA分析结论的科学性和有效性。因子分析的降维整合功能可以降低指标之间的强线性关系，因子分析和DEA方法的结合为高校效率评价的研究提供了有意义借鉴。

［1］Timothy J.Coelli，D.S.Prasada Rao，eg.效率和生产效率分析导论［M］.刘大成，译.北京:清华大学出版社，2009:147，150.

［2］彭江.论高等学校管理的“学校失灵”及出路［J］.清华大学教育研究，2004，25(4):50-52.

［3］谢南斌，田金信.基于AHP/DEA的高职教育效率评价研究［J］.江苏技术师范学院学报:自然科学版，2008，14(4):63-65.

［4］金晶.英国职业教育评估体系述略［J］.绍兴文理学院学报:教育教学研究，2011(2):64-67.

［5］林海明.因子分析中一些常见问题的解析［J］.统计与决策，2012，363(15):66-67.

［6］李英，邹燕，蒋舟.新会计准则下公允价值运用的动因探索——基于问卷调查与因子分析［J］.会计研究，2012(2):34-36.

［7］赵树宽，余海晴，巩顺龙.基于DEA方法的吉林省高技术企业创新效率研究［J］.科研管理，2013，34(2):37-38.

［8］王中昭.DEA与DRF法的整合［J］.运筹与管理，2006，15(2):41-44.