城市道路交通噪声的混沌特征及其应用

张文会，罗文文，李 卓，徐慧智

(1. 东北林业大学 交通学院，黑龙江 哈尔滨 150040；2. 北京交通运输职业学院 汽车工程系，北京 102618)



城市道路交通噪声的混沌特征及其应用

张文会1，罗文文1，李 卓2，徐慧智1

(1. 东北林业大学 交通学院，黑龙江 哈尔滨 150040；2. 北京交通运输职业学院 汽车工程系，北京 102618)

通过采集城市道路特征断面的交通噪声，形成时间序列，采用自相关函数法计算延迟时间，当相关系数衰减为0.4时，计算得到相空间重构的延迟时间为12。利用两组噪声样本的训练集计算关联维数，当嵌入维数为6时，关联维数保持不变，确定系统的嵌入维数为3，从而判定两组交通噪声样本存在混沌特征。根据重构的相空间、状态点及临近点计算拟合参数，分别对两组噪声样本进行混沌预测，并与检验集比对，结果表明：混沌模型可以用于短时城市道路交通噪声预测，两组噪声样本的预测平均相对误差分别为8.56%和9.33%。

交通工程；城市道路；交通噪声；混沌特征；相空间重构

汽车保有量增加和城市的发展使道路不断拓宽和延伸，道路格局发生变化，以满足出行需求。交通噪声由于其危害性、连续性和遍及性日益受到关注[1]，目前关于交通噪声的研究主要从噪声辐射和传播过程中的声衰减与有关参量的关系[2-3]、噪声的时间分布和空间分布[4-5]等方面展开。

城市道路交通噪声是由系统多因素相互耦合作用的综合反映，如交通流量、交通组成、平均速度和环境等，基于以上多元参数可建立噪声的预测模型[6-8]。由于交通系统本身是开放、时变的复杂系统，交通噪声也具有非线性和不确定性，看似随机的噪声时间序列，实际包含着混沌运动的基本信息。混沌运动要在三维以上的系统中才能描述，因此要把不规律的交通噪声时间序列拓展到多维相空间中，以揭示城市道路交通噪声时间序列的混沌特征。笔者基于相空间重构理论，判别城市道路短时交通噪声时间序列的混沌特征，并利用混沌模型对检验集进行预测。

1 城市道路交通噪声的采集

交通噪声的采集地点为城市道路平直路段，距离前后方交叉口500 m以上。采集设备为AWA5610D型积分声级。为比对采样时间与混沌特性的关系，采样时间分别设定为20，40 s，连续记录噪声值。其他试验条件如表1。采集到的噪声时间序列值如图1。

表1 交通噪声采集条件

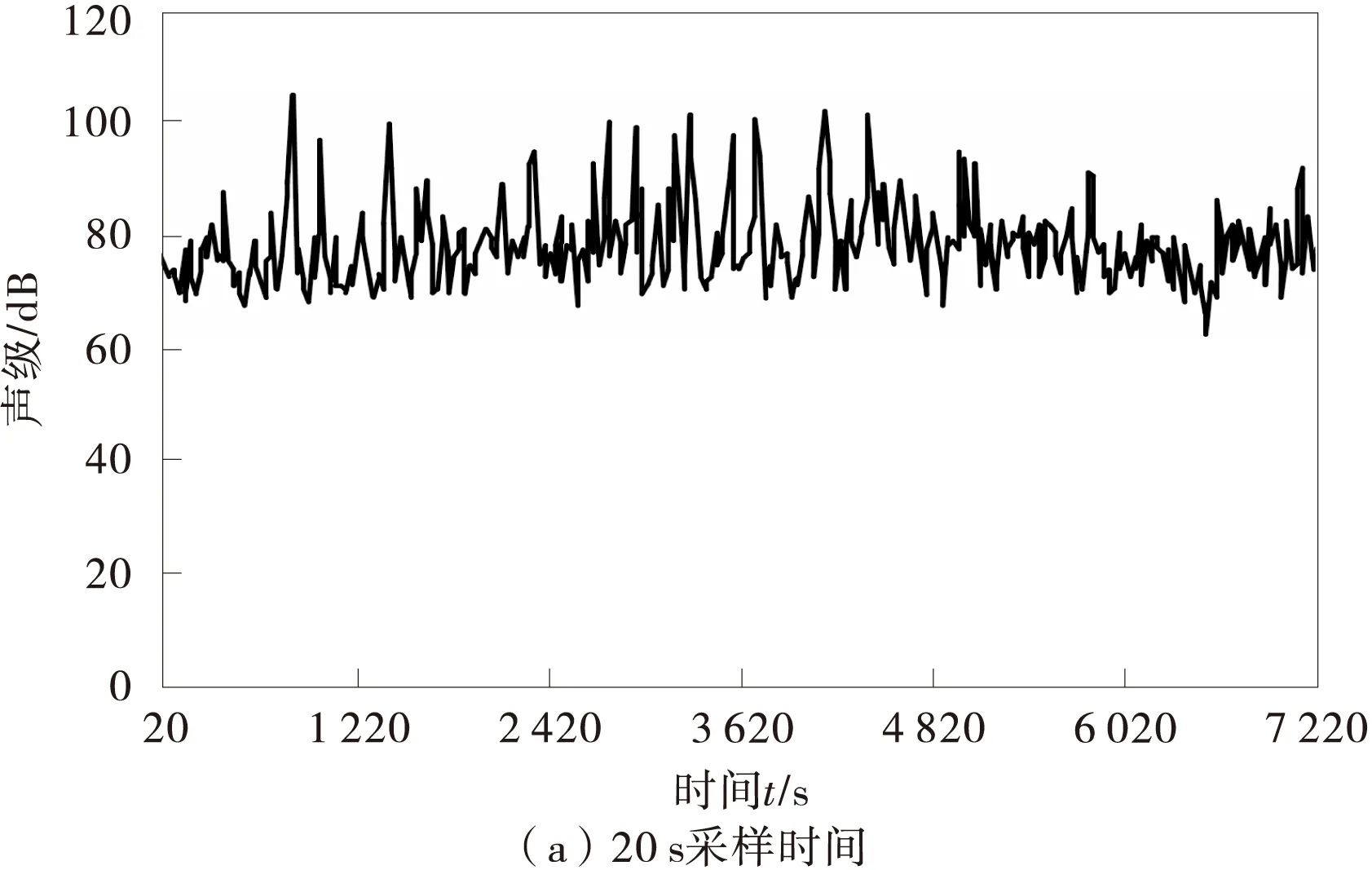
图1 城市道路交通噪声时间序列

2 相空间重构理论和延迟时间

一般认为，混沌就是一种低阶确定性的非线性动力系统所表现出来的复杂行为。从数学上讲，对于确定的初始值，由动力系统就可以推知该系统的长期行为，甚至追溯其过去形态。

2.1 相空间重构理论

相空间重构是根据有限的数据来重构吸引子，以研究系统动力行为的方法。其基本思想是：系统中任一分量的演化都是由与之相互作用的其他分量所决定的，这些分量的信息隐含在任一分量的发展过程中。

设(N,ρ),(N1,ρ1)是两个度量空间，如果存在映射φ:N→N1满足：①φ满射；②ρ(x,y)=ρ1(φ(x),φ(y))(∀x,y∈N)，则称(N,ρ),(N1,ρ1)是等距同构的。

如果(N1,ρ1)与另一度量空间(N2,ρ2)的子空间(N0,ρ2)是等距同构的，则称(N1,ρ1)可以嵌入(N2,ρ2)。

M是d维流形，φ:M→M,φ是一个光滑的微分同胚，y:M→R,y有二阶连续导数，φ(φ,y):M→R2d+1，其中：φ(φ,y)=(y(x),y(φ(x)),y(φ2(x)),…,y(φ2d(x))则φ(φ,y)是M到R2d+1的一个嵌入[9]。

上述定理简而言之就是把具有混沌特性的时间序列重建为一种低阶非线性动力学系统，通过相空间重构，可以找出混沌吸引子在隐藏区的演化规律，使现有的数据纳入某种可描述的框架之下，从而为时间序列的研究提供一种方法和思路。

设一个m维的动力系统可由式(1)表示：

(1)

通过消元可将式(1)变成一个m阶的微分方程：

x(m)=f(x,x(1),…,x(m-1))

(2)

它相当于描述时间演化：

(3)

将其离散化并用差分方程代替各阶导数，作适当简化后有：

(4)

式中：τ为延迟时间；m为嵌入维数。

式(1)～式(4)即为延滞时间重构的相空间。

2.2 延迟时间的确定

对于无限长的时间序列，可以任意选择延迟时间τ，但实际时间序列一般是有限长的，因此在相空间重构过程中τ值的选取很重要，笔者采用自相关函数法计算延迟时间，自相关系数定义为：

(5)

一般取自相关系数衰减到一个较小的值时所对应的τ值作为延迟时间，而这个较小值不能选择太小，否则对应的时间延迟会很大。文献[10]中给出了一个合理的经验值为1/e，约为0.4。

根据采集到的交通噪声时间序列，参照式(5)，得到采样时间分别为20，40 s时自相关系数，如图2。

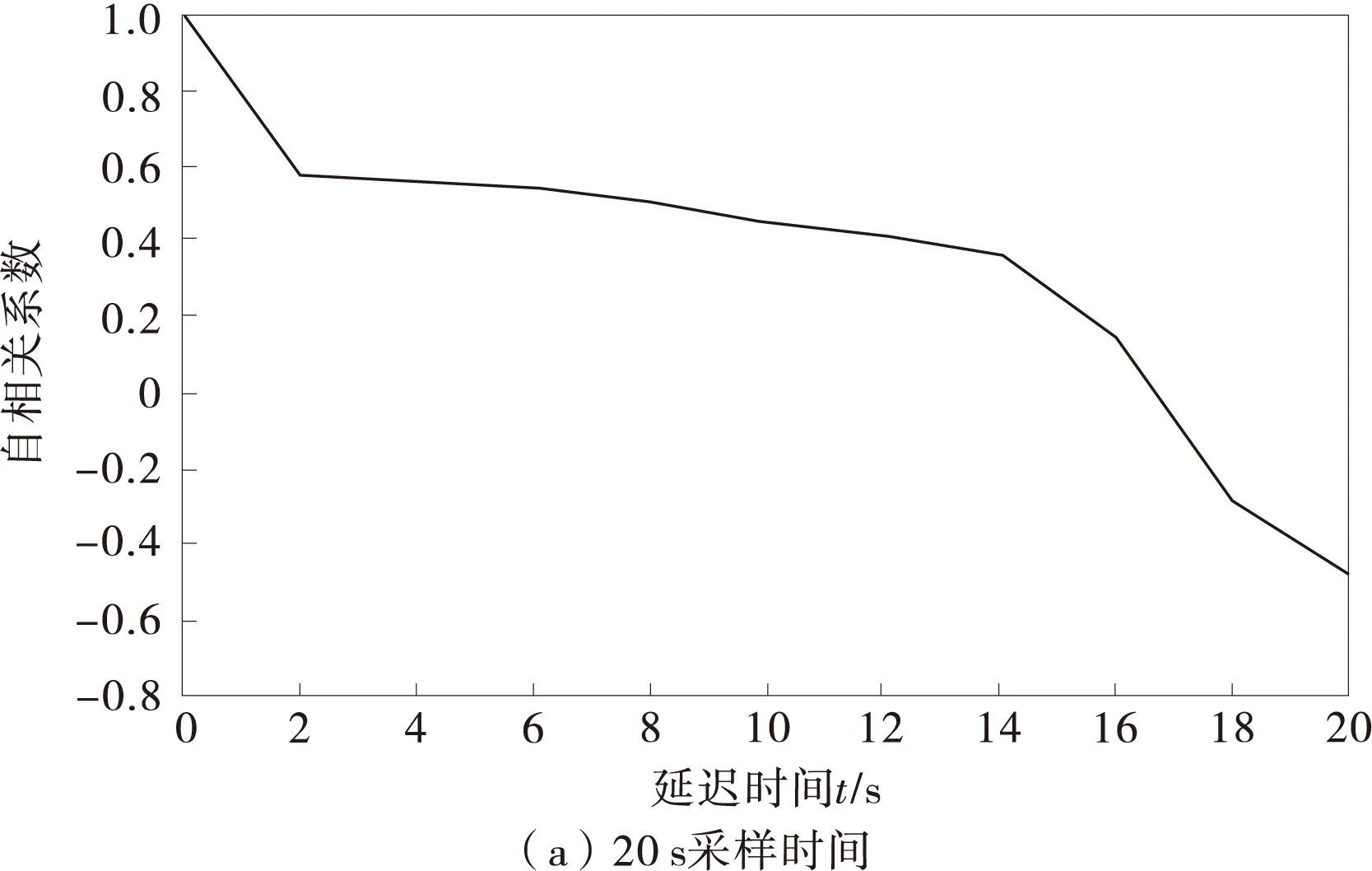
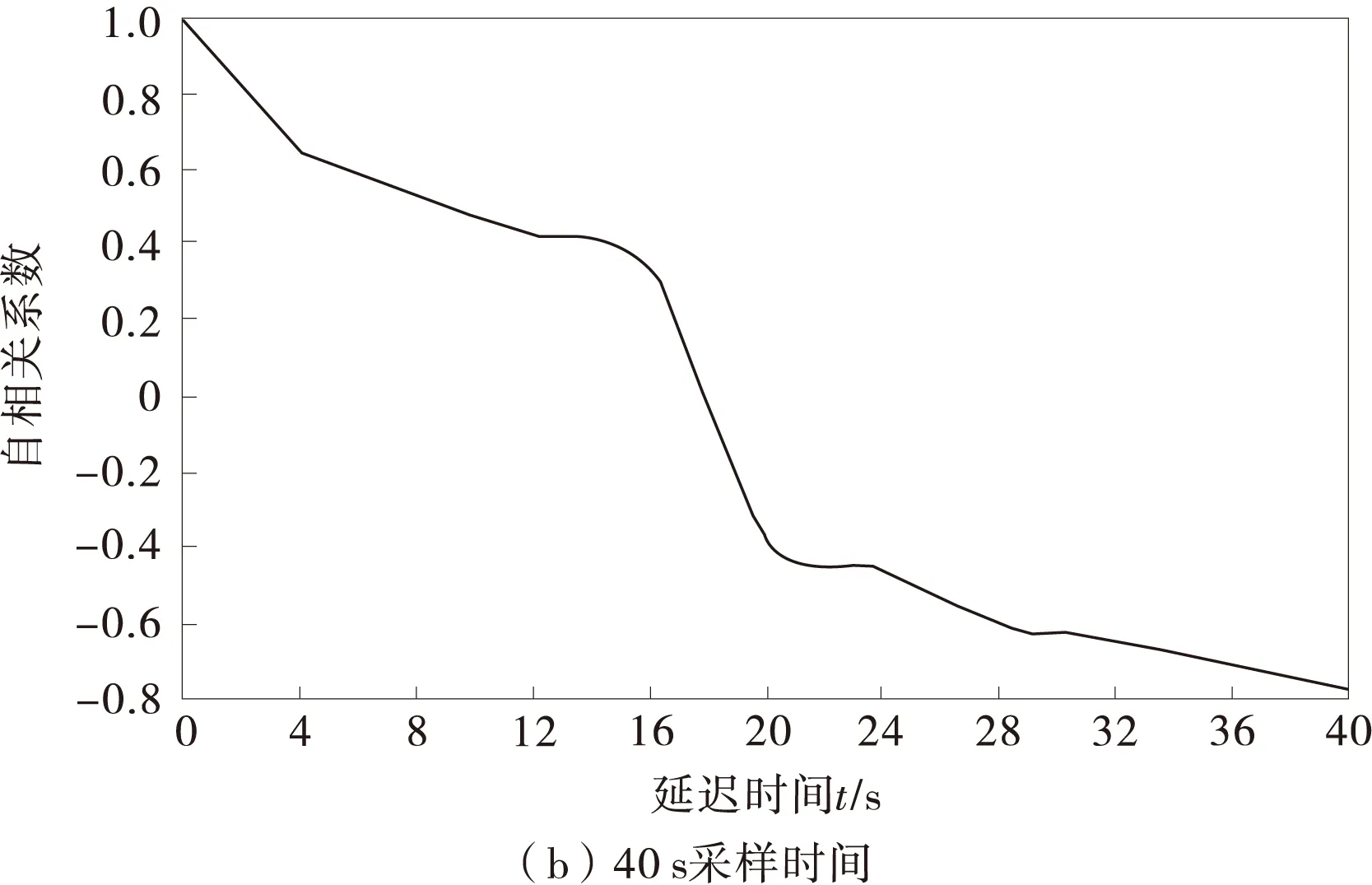
图2 自相关系数

由图2可知，当延迟时间为τ=12 s时，自相关系数衰减为0.4左右，因此选择τ=12 s为重构交通噪声系统的延迟时间。

3 城市道路交通噪声的混沌判定

3.1 关联维数

关联维数是判别吸引子类型以及复杂程度的表征量，它可以描述系统在整个变化中稳定性和确定性的程度，同时也确定了描述系统所需独立变量的个数。考察m维(m足够大) 重构相空间中的两点：

设它们的距离为rij(m)，则该距离是一个m维的函数，且有：

(6)

给定一个距离r，并且计算所有距离小于r的相点对数占所有相点对数的比例，记为：

(7)

式中：θ是Heavisible函数，即：

(8)

显然,C2(r，m)是一个累计函数，它描述了吸引子上两点距离小于r的概率，表明某点(参照点) 距离小于r的相点的聚集程度，所以称C2(r,m)为关联函数。一般r的选取要保证0

(9)

由于式(9)的比例关系与选择的探测量δ的大小没有关系，所以可以选择比例系数为1。

则有：

C2(r,m)=(r)D2

(10)

可以求出：

(11)

由式(11)可得，D2(m)是嵌入维数的函数，一般称为关联维数的估计值。在求解时，一般增加嵌入维数的值，求出不同嵌入维数下关联维数的估计值，直到估计值不再随嵌入维数的增大而改变为止，此时的嵌入维数称为饱和嵌入维数mc。这在lnC2(r,m)-lnr图中表现为斜率不再发生变化，此时的斜率就是所要求的关联维数D2=D2(mc)。

如果估计值随m的增长而增长，并不收敛于一个稳定的值，则表明所考虑的系统是一个随机时间序列。而关联维数的存在表明系统具有混沌特性，并为相空间重构中嵌入维数的选择提供了依据。

3.2 混沌特性的判定

采样时间为20s(360个噪声值)时，利用前300个时间序列值作为训练集来构造初始相空间，余下的60个值(检验集)用于检验模型精度。将m值由1依次递增至6，分别获得lnC2(r,m)与lnr关系图。限于篇幅，只列出m=6时二者的关系(图3)。

图3 lnC2(r,m)与lnr的关系(m=6)

由图3可知，当嵌入维数为6时，曲线的斜率接近不变，即关联维数保持为5.344 68E-08，从而可以确定20 s采样时间交通噪声序列的饱和嵌入维数为6。在混沌预测时，一般选取饱和嵌入维数的1/2作为系统的嵌入维数(当饱和嵌入维数为奇数时，选取饱和嵌入维数1/2的下一位整数作为系统的嵌入维数)，因此确定系统的嵌入维数为3。由此可判定，交通噪声时间序列存在混沌现象。

同理，采样时间为40 s时，交通噪声时间序列的饱和嵌入维数也为6，系统的嵌入维数为3。

4 城市道路交通噪声的混沌预测

4.1 混沌预测理论

如果在重构的相空间中，将交通噪声时间序列特征轨迹恢复，通过对该轨迹的拟合，即可得到映射：

X(k+1)=f(X(k))

(12)

式中：X(k)是相空间中的点。

设相空间嵌入维数为m，则：

(13)

预测算法如下：

1)确定交通噪声时间序列的嵌入维数m和延迟时间τ。

2)重构交通噪声系统, 将时间序列x(n),n=1,2,…,N进行转化：

式中：k=N-(m-1)τ。由所有向量的分量组成的空间为相空间，交通噪声时间序列转化为相空间中的点。

3)寻找最近邻，假设当前的状态点为X(j)，通过计算各点与X(j)的欧氏距离找出p个最近邻点X(i1),X(i2),…,X(ip)。

4)找出所有p个最近邻的下一个相点X(i1+1),X(i2+1),…,X(ip+1)。在这个小邻域内对相空间轨迹进行线性拟合，即求出下式中的系数A，B：

拟合求得A,B后，通过X(j+1)=A+BX(j)得到相空间中轨迹的趋势，从而求出交通噪声时间序列中x(j+1+(m-1)τ)的预测值。

4.2 交通噪声的混沌预测

根据计算结果，选择重构相空间的嵌入维数m=3，延迟时间τ=12，对20s采样时间的交通噪声时间序列进行相空间重构，得到维数为3的相空间，其中相点个数k=N-(m-1)τ=276。对检验集中的60个点进行预测。假设当前的状态点为X(270)，分别计算各点与X(270)的欧氏距离ρ=(X(270)-X(i))(0

建立系数矩阵：

拟合求得A=-0.69，B=1.05。通过公式X(j+1)=A+BX(j)分别求得x301到x360的数值，绘制预测值曲线并与实际值进行比较见图4。

图4 预测值与实测值

平均相对误差：

8.56%

由图4，实际值和预测值相差不大，城市道路交通噪声时间序列混沌预测结果平均相对误差为8.56%，精度较高。同理，对于40 s采样时间的交通噪声时间序列进行混沌预测，平均相对误差为9.33%。

5 结 语

城市道路交通噪声与多因素相关，笔者采集了交通噪声时间序列值，应用相空间重构理论获得了关联维数和嵌入维数，证明了噪声序列具有混沌特性。最后利用混沌模型对短时城市道路交通噪声进行预测和比对，预测精度较高。城市道路交通噪声的混沌行为是否存在与采样时间关系不大，但与混沌预测的精度有关。随着样本量的增加，相空间中相点的密度相应增加，近邻相点的选择会更加合理，预测精度也会提高。

[1] 肖裕民.城市交通满意度定量化评价方法探讨[J].重庆交通大学学报:自然科学版,2009,28(1):111-115. Xiao Yumin.Discussion on quantitative evaluation method of urban traffic satisfaction [J].Journal of Chongqing Jiaotong University:Natural Science,2009,28(1):111-115.

[2] 李超,刘小明,荣建.道路交通噪声计算机仿真模型[J].武汉理工大学学报:交通科学与工程版,2010,34(2):350-353. Li Chao,Liu Xiaoming,Rong Jian.Road traffic noise computer simulation model [J].Journal of Wuhan University of Technology:Transportation Science & Engineering,2009,34(2):350-353.

[3] 常玉林,王炜.环形交叉口交通噪声预测模型[J].交通运输工程学报,2003,3(1):80-83. Chang Yulin,Wang Wei.Traffic noise forecasting model at roundabout [J].Journal of Traffic and Transportation Engineering,2003,3(1):80-83.

[4] Doygun H,Gurun D K.Analyzing and mapping spatial and temporal dynamics of urban traffic noise pollution:a case study in Kahramanmara,Turkey [J].Environmental Monitoring and Assessment,2008,142(1/2/3):65-72.

[5] Jamrah A,Al-Omari A,Sharabi R.Evaluation of traffic noise pollution in Amman,Jordan [J].Environmental Monitoring and Assessment,2006,120(1/3):499-525.

[6] 韩善灵,朱平,林忠钦.道路交通噪声评价及预测新方法[J].交通运输工程学报,2005,5(3):111-114. Han Shanling,Zhu Ping,Lin Zhongqin.Evaluation and prediction new methods of road traffic noise [J].Journal of Traffic and Transportation Engineering,2005,5(3):111-114.

[7] 刘小明,李超,荣建.道路交通噪声预测模型研究[J].北京工业大学学报,2009,35(7):953-959. Liu Xiaoming,Li Chao,Rong Jian.Review in road traffic noise prediction model study [J].Journal of Beijing University of Technology,2009,35(7):953-959.

[8] 袁玲.交通噪声预测的神经网络模型[J].长安大学学报:自然科学版,2003,23(2):84-87. Yuan Ling.Neural network for predicting traffic noise [J].Journal of Chang’an University:Natural Science Edition,2003,23(2):84-87.

[9] 修春波,刘向东,张宇河.相空间重构延迟时间与嵌入维数的选择[J].北京理工大学学报:自然科学版,2003,23(2):219-224. Xiu Chunbo,Liu Xiangdong,Zhang Yuhe.Selection of embedding dimension and delay time in the phase space reconstruction [J].Tranasaltions of Beijing Institute of Technology:Natural Science Edition,2003,23(2):219-224.

[10] 刘力军,李松,解永乐.短时交通流混沌预测模型的比较研究数学的实践与认识,2011,41(17):106-114. Liu Lijun,Li Song,Xie Yongle.Comparative study on chaotic prediction model in short-term traffic flow [J].Mathematics in Practice and Theory,2011,41(17):106-114.

Chaotic Characteristics and Application of Traffic Noise of Urban Road

Zhang Wenhui1, Luo Wenwen1, Li Zhuo2, Xu Huizhi1

(1. School of Traffic, Northeast Forestry University, Harbin 150040, Heilongjiang, China; 2. Department of Automobile Engineering, Beijing Vocational College of Transportation, Beijing 102618, China)

Traffic noise was composed of time series, which was collected at certain section in urban road. Autocorrelation function was used to calculate the delay time. When the autocorrelation coefficient attenuated to 0.4, the delay time to reconstruct phase space was 12. The training set included two groups of noise samples was employed to calculate the correlation dimension. When embedding dimension was 6, the correlation dimension kept invariant. Therefore, the embedding dimension of system was 3 and traffic noise samples were of chaotic characteristics. Based on the reconstructed phase space, state points and near points, the fitting parameters were calculated. The two groups of traffic noise samples were predicted respectively by chaotic models and then compared the results with those got by the training set. The results show that chaotic models are suitable to predict the traffic noise of urban road in a short time. The average relative errors of two groups of noise samples were 8.56% and 9.33% individually.

traffic engineering; urban road; traffic noise; chaotic characteristics; phase space reconstruction

10.3969/j.issn.1674-0696.2015.01.25

2013-08-09；

2014-01-06

国家自然科学基金项目(51108137)

张文会(1978—)，男，黑龙江哈尔滨人，副教授，博士后，主要从事交通环境与安全技术方面的研究。E-mail：rayear@163.com。

U491.9

A

1674-0696(2015)01-116-05