基于重力刚度法的三塔悬索桥形变特征研究

王立彬，吴 勇，金泊含

(南京林业大学 土木工程学院，江苏 南京 210037)



基于重力刚度法的三塔悬索桥形变特征研究

王立彬，吴 勇，金泊含

(南京林业大学 土木工程学院，江苏 南京 210037)

应用重力刚度法推导了集中力和均布载荷作用下三塔四跨悬索桥主缆的无量纲位移的理论表达式；分析了跨数、边中跨比以及恒载和活载集度对三塔四跨悬索桥重力刚度挠度的影响规律，及三塔四跨悬索桥不同于两塔悬索桥的新特征。研究表明：多跨悬索在恒活载作用下主缆的力学特征主要决定了三塔四跨悬索桥整体结构刚度的基本特征，单跨悬索和多跨悬索力学行为的差异是两塔和三塔悬索桥力学特征差异产生的根本原因；应用重力刚度法分析的三塔悬索桥行为特征与基于有限元方法计算的结构行为特征有很好的一致性。

桥梁工程；重力刚度法；位移方程；三塔四跨；悬索桥；挠度分析

0 引 言

作为悬索桥的重要承重构件，主缆在恒载作用下产生了很大的初始张力，形成了稳定的初始构形，对进一步抵抗竖向活载变形提供了强大的“重力刚度”。加劲梁的抗弯刚度远远小于主缆的重力刚度，因而对全桥结构行为的影响处于次要地位。基于此，S.G.Buonopane把主缆、塔柱划分为第一承重体系，加劲梁和吊杆划分为第二承重体系[1]。我国学者对重力刚度的定义和计算方法的研究表明：主缆的力学特性主要地决定着全桥的结构行为，重力刚度法是揭示大跨悬索桥基本力学行为的有效方法[2-4]。但是，相关研究均假定主缆两端水平铰接，因而主要针对单跨悬索桥的重力刚度展开研究。

随着泰州大桥、马鞍山大桥和鹦鹉洲长江大桥等多塔多跨悬索桥的建设，多塔连跨悬索桥的研究日益成为土木工程界研究热点问题之一。国内学者[5-9]展开了大量研究，但是研究多针对主边塔刚度、矢跨比等重要参数，以及加劲梁体系如全漂或固结体系等第二体系参数，乃至中央扣和弹性索等特殊构造参数等对悬索桥动静力力学行为的影响。并且由于多塔多跨悬索桥体系的复杂性，研究都是基于有限元方法展开，因而研究结果是多跨悬索桥索-塔-梁组合结构在荷载作用下的整体行为特征。

然而，在悬索桥整体结构力学特征中，各组成构件对整体结构力学行为的影响有着本质区别，需要逐一分类研究。由于主缆是第一承重体系的关键构件，主缆的力学特性主要决定多塔多跨悬索桥不同于两塔悬索桥全桥的结构行为，因此研究多跨主缆的力学行为是深入揭示多塔多跨悬索桥区别于两塔悬索桥新的特征规律的基础，具有重要的理论意义。

N. J. Gimsing[10]分析了多跨悬索与单跨悬索的刚度特征差异，但没有提供详细的论证过程及方法。笔者引用A. Jennings[11]的基于重力刚度理论的分析方法，分析了三塔四跨悬索桥整体设计本征参数，即不同跨数和跨度的多跨悬索在不同恒、活载作用下的形变特征，研究三塔多跨悬索桥力学行为产生的原因和特征。

1 集中力作用下的无量纲位移方程

图1为一座三塔四跨悬索桥。桥跨和桥塔序号均从左至右依次排序，每一跨所受的恒载集度均相同，大小为wkN/m。悬索桥主缆线形为抛物线，两端固结。假设桥塔顶部不约束主缆的水平移动，从而保证成桥状态下的主缆初始水平力H和受活载后主缆的水平力增量h对于整座桥都是相同的。

图1 三塔四跨悬索桥示意

图1中，有一个集中荷载p作用于第2跨，根据挠度理论，应满足平衡方程式(1)和协调方程式(2)：

(1)

(2)

式中：ui为第i跨跨左端点位移；ui+1为第i跨右端点位移；E为主缆弹性模量；A为主缆截面面积；Lei为第i跨主缆长度，Lei≈li[1+8(di/li)2](di为第i跨矢高，li为第i跨的跨径)。

以挠度理论平衡和协调方程为基础，引入下列条件：

1)恒载沿全桥纵向均匀分布，且满足：w=

-H(d2y/dx2)；

2)忽略加劲梁抗弯刚度，即：EI=0；

3)忽略活载水平力非线性项；

4)忽略主缆的弹性变形，即：EA=0。

综合所有条件，得到挠度的重力刚度表达式：

(3)

根据挠度理论公式，忽略加劲梁刚度和缆索弹性形变，分析悬索桥静力响应的方法，即为重力刚度法[12]。

(4)

将式(4)代入式(3)中，经无量纲处理后得到：

(5)

式(5)即为三塔四跨悬索桥集中力作用位置处无量纲位移方程。

2 均布荷载作用下的无量纲位移方程

根据影响线方法布载计算均布荷载作用下结构的位移。为了得到受到活载q作用时的最大位移，必须将活载q施加在位移影响线为正的部位。图2 显示了受力跨单位荷载作用时的位移曲线，即位移影响线。

图2 均布荷载受力跨位移影响线

(6)

图2中，五边形ABCDE的面积为：

(7)

曲边梯形ACDE的面积为：

(8)

活载q施加后的位移v为：

v=q(AT-AP)

(9)

将式(7)、式(8)代入式(9)，并进行无量纲化处理，整理得到：

(10)

式(10)即为均布荷载作用下的无量纲位移方程。

3 多塔悬索桥的挠度分析

3.1 桥跨数的影响

参数α表达的是非受力跨对受力跨的影响。当α=1，表示一座单跨悬索桥；当α=0，则表示一座超多跨甚至是无限跨悬索桥。

图3 展现了不同α值与受力跨不同位置处无量纲位移的关系。显然，无论是集中力作用还是均布荷载作用，α的取值越大，无量纲位移越小。说明跨数的增加和边跨的存在都会增加悬索桥的挠度。

图3 受力跨无量纲位移受α影响

值得注意的是，在公式推导中，并没有考虑中塔的影响，缆索在鞍座处可以水平自由滑动。然而，正是这一假设，却揭示了多塔悬索桥相邻跨之间最本质的关系特征。受力跨主缆在各跨主缆水平拉力不变的情况下，协调索自身和邻跨主缆的几何形变特征并依次传递，最终形成了稳定的受力状态，反映了不同跨缆索自身形变协调渐次平衡的本质特征。

分析表明，跨数的增加必然导致加载跨挠度的增加，这是多塔多跨悬索桥的本质特征，解决的方法就是增加中塔的抗推刚度，以减少塔顶水平位移，在邻跨主缆通过缆索倾角和跨度变化达到自身平衡的基础上，提高塔的抗推刚度对挠度的影响。

3.2 边中跨比的影响

和跨数一样，边跨比也影响着参数α的大小。为直观起见，将无量纲位移转化为绝对挠度，分析边中跨比、恒载集度和均布荷载布置长度对三塔两跨悬索桥和三塔四跨悬索桥的重力刚度挠度的影响。

图4为双向六车道的两塔三跨悬索桥及三塔四跨悬索桥的计算模型。两桥主跨跨径为l，边中跨比为a，主缆材料为钢，弹性模量E=210 GPa，恒载集度均为wkN/m。两桥的活载依据现行的JTG D60—2004《公路桥涵设计通用规范》的公路-I级荷载计算。

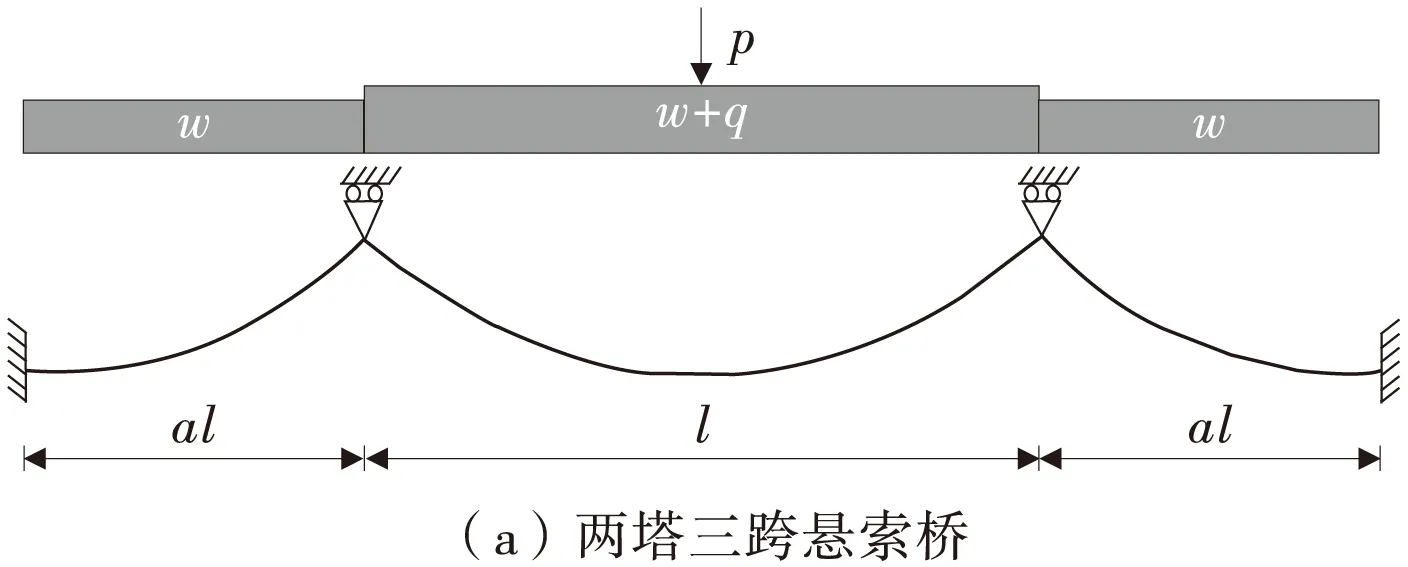
图4 两塔三跨及三塔四跨悬索桥计算模型

取一座主跨跨径为1 000 m的两塔三跨悬索桥，若边中跨比a为0.1，0.2，0.3，0.4和0.5，则主跨相应α值是0.998 0，0.984 2，0.948 8，0.886 5和0.800 0，对于三塔四跨悬索桥，主跨相应α值是0.499 5，0.496 0，0.486 9，0.469 9和0.444 4。显然与三跨悬索桥比较，α值显著减小，约为两塔三跨悬索桥α值的1/2。为了更直观地认识，图5 同时比较了主跨跨径为1 000 m和2 000 m的三跨悬索桥以及主跨跨径为1 000 m的三塔四跨悬索桥的重力刚度挠度。

图5 边中跨比对重力刚度挠度的影响

从图5可见，随着边跨长度的增加，主跨重力刚度挠度增加，这与图3所表达的变化规律是一致的。边中跨比变化范围在0.1～0.3之间时，重力刚度挠度的增加并不明显，故建议在设计时边中跨比的取值应在该范围内。边跨比超过0.3后，单跨2 000 m的悬索桥较单跨1 000 m的两塔三跨悬索桥增量显著，但是三塔四跨悬索桥的重力刚度挠度增量并不显著。

比较相同主跨跨径的两塔三跨悬索桥和三塔四跨悬索桥的重力刚度挠度，两塔三跨悬索桥的重力刚度挠度远小于三塔四跨悬索桥。A. G. Pugsley[12]通过有限元分析也证明了这一点。根据《公路悬索桥设计规范》(报批版，2002年)，悬索桥由汽车荷载引起的最大竖向挠度值不宜大于跨径的1/250～1/300。根据图6的计算结果，传统两塔三跨悬索桥满足要求，而三塔四跨悬索桥远不能满足要求。这就说明，对于传统两塔三跨悬索桥，依靠主缆的重力刚度已可以满足规范的挠度限制要求，对桥塔刚度和加劲梁抗弯刚度等其他构件的刚度要求相对降低。崔冰，等[7]利用有限元软件分析后也得出相同的结论，在设计时可以设计为柔性塔和扁平箱梁。

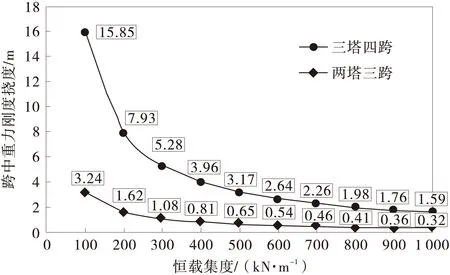
图6 恒载集度对重力刚度挠度影响

相反，对于三塔四跨悬索桥，依靠主缆的自身的重力刚度远不能满足规范的挠度限制要求，需要协同桥塔和加劲梁等其他构件一起作用来降低最大竖向挠度以满足规范要求。三塔四跨悬索桥对除了主缆重力刚度之外的其他刚度要求更高，在设计时应相对强化其他构件刚度，如提高中塔抗推刚度，减少矢跨比，或采取连续加劲梁等方式提高结构刚度。这一结论与文献[5-6，9]通过有限元软件分析后的结果相同。

3.3 恒载集度比的影响

恒载主要由主缆的自重及加劲梁的自重两部分组成。在悬索桥设计计算过程中，恒载是一个十分重要的设计参数。这一参数不仅影响了悬索桥的静力性能，同时也影响了悬索桥建设的经济性。图6展示了不同恒载集度值对传统的两塔三跨悬索桥及新型三塔四跨悬索桥静力性能的影响，特别是加载跨跨中重力刚度挠度的影响。

由图6可以看出，恒载集度的增加对与加载跨跨中重力刚度挠度是有利的，且这一有利影响在恒载集度w<500 kN/m时尤为明显。当恒载集度w>500 kN/m时，恒载集度的增加对加载跨跨中重力刚度挠度的影响很小。这一现象就说明，在恒载集度较小时，增加恒载集度即增加主缆和主梁的重量会明显增加整体结构的重力刚度，从而达到了减小挠度的效果。钱炜，等[14]对两塔三跨悬索桥利用有限元软件分析后也得出增大恒载可减小结构变形的相同结论。

三塔四跨悬索桥当恒载集度从100 kN/m增至200 kN/m，跨中重力刚度挠度从15.85 m减小到了7.93 m，挠度减小了50%，效果非常明显。传统的两塔三跨悬索桥当恒载集度从100 kN/m增至200 kN/m，跨中重力刚度挠度从3.24 m减小到了1.62 m，挠度也减小了50%，效果也非常明显。但是考虑到为了满足规范要求的最大挠度要求，显然这一影响对于三塔四跨悬索桥更为突出。因此，在设计悬索桥时，选择合适的恒载集度对于悬索桥的静力性能是十分关键的因素。结合图6，笔者认为两塔三跨悬索桥合理的恒载集度取值范围为100～300 kN/m，而三塔四跨悬索桥合理的恒载集度取值范围为200～500 kN/m，因此三塔四跨悬索桥更适合上下两层车道的双层悬索桥。

3.4 活载布载长度的影响

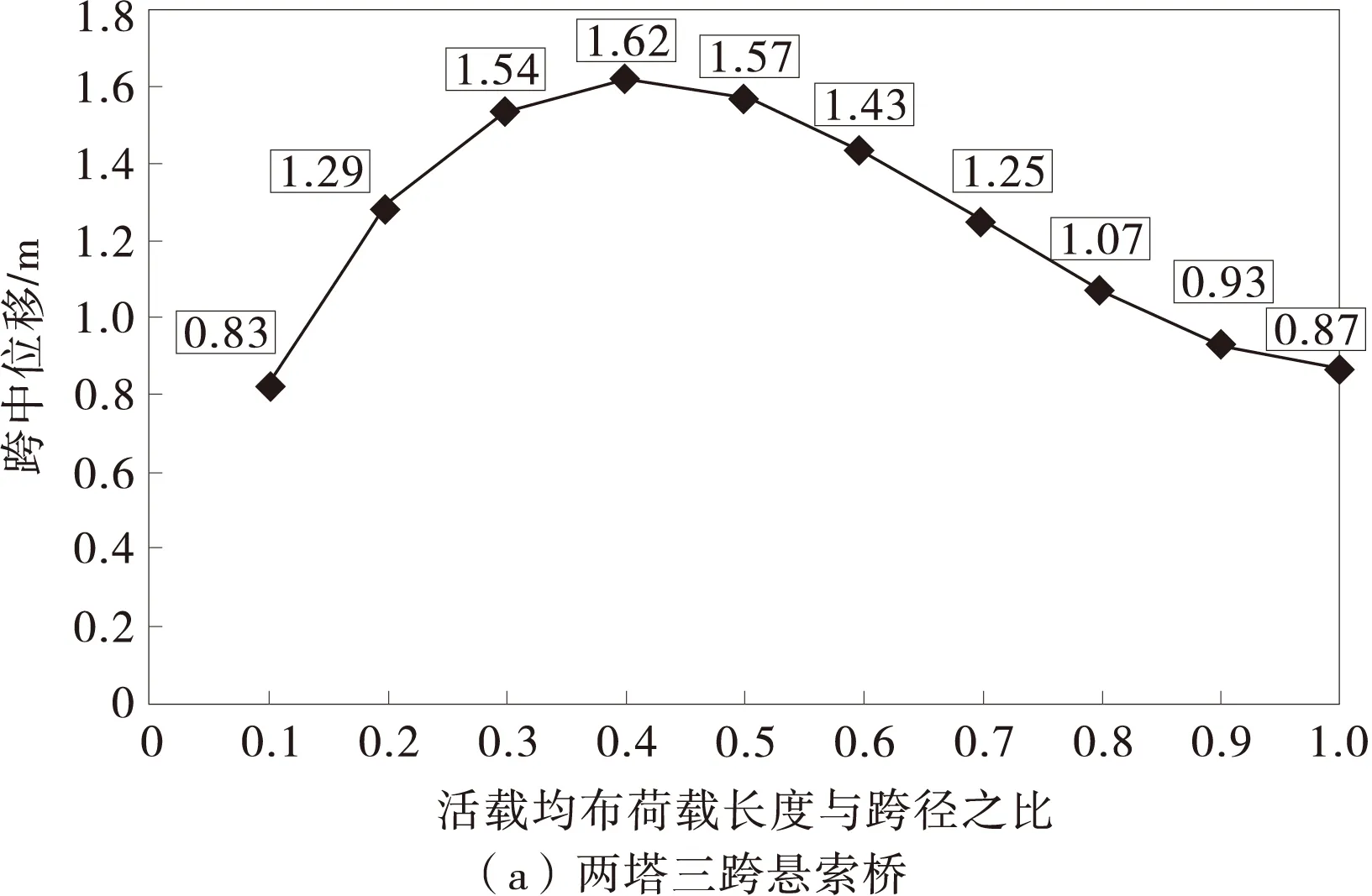
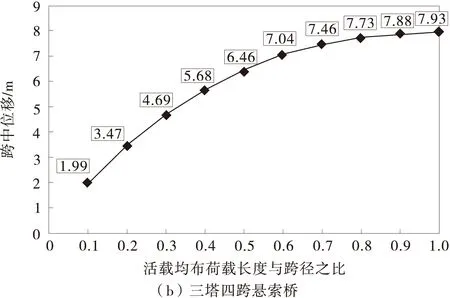
图7 最大竖向位移v与活载分布关系

图7(a)的变化曲线存在明显的极值点。当均布荷载布载长度为0.4l时，跨中重力刚度挠度达到了极值。故在设计两塔三跨悬索桥时，除了考虑常规的满布荷载时的挠度，也应考虑只布置0.4l长度均布荷载时的挠度。而在图7(b)中却并不存在这样的极值点，跨中重力刚度挠度随着均布荷载布载长度的增加而增大，即三塔四跨悬索桥的最不利布载方式是单一主跨满布荷载而另一主跨空载的情形。这一结结论与张劲泉，等[15]及刘晓銮[16]利用有限元软件分析得到结论是相同的。

4 结 论

1)在多塔多跨悬索桥结构中，桥跨数量和边跨影响悬索桥的挠度，跨数越多或边跨越长悬索桥挠度越大。

2)从单跨悬索桥到多跨悬索桥最大位移位置产生了变化，即位移影响线从双峰转变成单峰。

3)多塔多跨悬索桥单纯依靠主缆的重力刚度不能满足规范挠度要求，需要结合主塔抗推刚度和主梁抗弯刚度等其他构件一同作用；相反，传统两塔三跨悬索桥单纯依靠主缆的重力刚度已能满足规范挠度要求，对桥梁其他构件刚度要求较低。

4)在多塔多跨悬索桥结构中，恒载集度的增加会减小挠度。

5)传统两塔三跨悬索桥存在除满布荷载之外的最不利布载方式，即加载长度为0.4l的均布正对称荷载；相反，三塔四跨悬索桥的最不利布载方式就是一主跨满布荷载，另一主跨空载。

6)应用重力刚度法对多跨悬索进行理论分析，得到的多跨悬索桥的力学行为特征与现有诸多文献中对悬索桥整体结构有限元方法计算所得的力学特征有很好的一致性，说明主缆的力学行为特征决定了多跨悬索桥的根本特征。

[1] Buonopane S G,David P B. Theory and history of suspension bridge design from 1823 to 1940 [J]. Structural Engineering,1993,119(3):954-977.

[2] 徐君兰,向中富.关于悬索桥的重力刚度[J].重庆交通学院学报,2000,19(2):71-74. Xu Junlan,Xiang Zhongfu. Discussing gravity stiffness of suspension bridge [J]. Journal of Chongqing Jiaotong University,2000,19(2):71- 74.

[3] 肖恩源.论悬挂索的重力刚度[J].公路,2000 (8):43-49. Xiao Enyuan. Discussing gravity stiffness of suspension cable [J]. Highway,2000 (8):43-49.

[4] 刘钊,刘厚军.悬索桥主缆变形及重力刚度新算法[J].工程力学,2009,26(6):127-132. Liu Zhao,Liu Houjun. New arithmetic for cable deflection and gravity stiffness of suspension bridges [J]. Engineering Mechanics,2009,26(6):127-132.

[5] 张劲泉,曲兆乐,宋建永,等.多塔连跨悬索桥综述[J].公路交通科技,2011,28(9):30-45. Zhang Jinquan,Qu Zhaole,Song Jianyong,et al. Overview of multi-pylon multi-span suspension bridge [J]. Journal of Highway and Transportation Research and Development,2011,28(9):30-45.

[6] 阮静,吉林,祝金鹏.三塔悬索桥中塔结构选型分析[J].山东大学学报:工学版,2008,38(2):106-111. Ruan Jing,Ji Lin,Zhu Jingpeng. Structure style selection of the mid-tower of a three-tower suspension bridge [J]. Journal of Shandong University:Engineering Science,2008,38(2):106-111.

[7] 崔冰,林恰,于旭东,等.桥塔刚度对悬索桥的影响分析[J].中国工程科学,2010,12(7):33-38. Cui Bing,Lin Qia,Yu Xudong,et al. Influence analysis of tower stiffness on suspension bridge [J]. Engineering Sciences,2010,12(7):33-38.

[8] 梁鹏,吴向男,李万恒,等.三塔悬索桥纵向约束体系优化[J].中国公路学报,2011,24(1):59-67. Liang Peng,Wu Xiangnan,Li Wanheng,et al. Longitudinal constraint system optimization for three-tower suspension bridge[J]. China Journal of Highway and Transport,2011,24(1):59-67.

[9] 江南,沈锐利.矢跨比对悬索桥结构刚度的影响[J].土木工程学报,2013,46(7):90-97. Jiang Nan,Shen Ruili. Influence of rise-span ratio on structural stiffness of suspension bridge [J].China Civil Engineering Journal,2013,46 (7):90-97.

[10] Gimsing N J. Cable Supported Bridges Concepts and Design [M]. New York:John Wiley & Sons,1997.

[11] Jennings A. Gravity stiffness of classical suspension bridges [J]. Journal of Structural Engineering,1983,109 (1):16-36.

[12] Pugsley A G. The gravity stiffness of a suspension bridge cable [J]. The Quarterly Journal of Mechanics and Applied Mathematics,1952,5(3):385-394.

[13] 梁鹏,吴向男,李万恒,等.三塔悬索桥静动力特性与中塔选型[J].交通运输工程学报,2011,11(4):29-35. Liang Peng,Wu Xiangnan,Li Wanheng,et al. Static and dynamic properties of three-tower suspension bridge and structural type selection of mid-tower [J]. Journal of Traffic and Transportation Engineering,2011,11(4):29-35.

[14] 钱炜,汪磊.柔性悬索桥静力分析[J].现代交通技术,2009,6(1):52-54. Qian Wei,Wang Lei. Static analysis on flexible suspension bridge [J]. Modern Transportation Technology,2009,6(1):52-54.

[15] 张劲泉,曲兆乐,宋建永,等.多塔悬索桥的两个主要控制指标及其计算工况[J].公路交通科技,2011,28(8):96-99. Zhang Jinquan,Qu Zhaole,Song Jianyong,et al. Two principal control indexes of multi-pylon suspension bridge and related calculation cases [J]. Journal of Highway and Transportation Research and Development,2011,28(8):96-99.

[16] 刘晓銮.三塔悬索桥静力挠度可靠度分析[J].重庆交通大学学报:自然科学版,2011,30(5):895-898. Liu Xiaoluan. Static deflection reliability analysis of three-tower suspension bridge [J]. Journal of Chongqing Jiaotong University:Natural Science,2011,30(5):895-898.

Deflection Characteristics of Three-Pylon Suspension Bridge Based on Gravity Stiffness Method

Wang Libin, Wu Yong, Jin Bohan

(School of Civil Engineering, Nanjing Forestry University, Nanjing 210037, Jiangsu, China)

The dimensionless deflection expressions of main cable for three-pylon-four-span suspension bridges under concentrated load and distributed load were derived by gravity stiffness method. Then the influence rule of the number of spans, the ratio of side span to main span, dead load and live load intensity on the gravity stiffness deflection of three-pylon-four-span suspension bridge was analyzed respectively. And the new characteristics of three-pylon-four-span suspension bridge which were distinguished from the conventional three-pylon-four-span suspension bridge were also analyzed. These conclusion indicates that the mechanical characteristics of the multi-span main cable under dead and live load determine the basic characteristics of structure stiffness of three-pylon-four-span suspension bridges; the different behavior between one-span cable and multi-span cable causes the difference of mechanical characteristics between two-pylon suspension bridges and three-pylon suspension bridges; and the behavior characteristics of three-pylon suspension bridges based on the gravity stiffness deflection method keeps well consistent with the behavior characteristics based on finite elements method on overall structure.

bridge engineering; the gravity stiffness method; displacement expressions; three-pylon-four-span; suspension bridges; deflection analysis

10.3969/j.issn.1674-0696.2015.01.02

2013-12-25；

2014-03-27

江苏省优势学科建设工程资助项目(PAPD)

王立彬(1970—)，男，河北辛集人，副教授，博士，主要从事桥梁工程方面的研究。E-mail:jhwlb@163.com。

吴 勇(1990—)，男，江苏无锡人，硕士研究生，主要从事桥梁设计理论方面的研究。E-mail:wy900516@qq.com。

U448.25 献标志码：A

1674-0696(2015)01-006-06