基底刻槽封装式光纤光栅传感器应变传递影响因素分析

申昊文，朱萍玉，许沛胜，施 维

(广州大学，机电设备状态监测与控制市重点实验室，广东广州 510006)



基底刻槽封装式光纤光栅传感器应变传递影响因素分析

申昊文，朱萍玉，许沛胜，施 维

(广州大学，机电设备状态监测与控制市重点实验室，广东广州 510006)

光纤光栅传感器大多经过封装后粘贴于被测结构表面使用，而封装基底和粘胶的存在，导致结构的真实应变与光纤光栅感测值之间出现偏差。建立了基底刻槽封装的光纤光栅传感器应变传递力学简化模型，推导出相应的平均应变传递率公式；分别分析了基底的长、宽、厚和基底材料弹性模量对光纤光栅传感器平均应变传递率的影响。结果表明，采用刻槽封装后的光纤光栅传感器平均应变传递率，在有效范围内随着基底长度的增加而增加，随着基底的宽、厚和材料弹性模量的增加而减小，为光纤光栅刻槽封装提供定量的指导。

光纤光栅；应变；传递率；影响因素；基底

0 引言

近年来，光纤光栅作为一种新型光无源器件，因其抗电磁干扰和抗化学腐蚀性强、寿命长、复用性好等优良特性，在工程结构监测中逐渐发展起来。但裸光纤光栅自身抗剪能力差，再加之光栅写入时紫外光使无涂敷的光纤变脆，很容易脆断。所以直接将其作为传感器将无法适应实际应用中的恶劣环境，如土木工程中粗放式施工。因此，对裸光纤光栅进行二次开发，即对其进行封装处理，是光纤光栅传感器实际应用中推广的一个重要环节[1]。

根据不同的被测结构，光纤光栅封装方式一般有表面直接粘贴[2]、直接埋入结构[3]、金属薄套管封装[4]、铝片封装[1]和铜片封装[5]、两端夹持固定[6]等方式。无论采取哪一种封装方式，都需要对裸光纤光栅部分进行胶接、涂敷层、或者是基底保护。但与裸光纤光栅相比，不同的胶接层、涂敷层、基底的物理特性存在一定的差异，进行不同封装后的光纤光栅传感器所测得的应变和结构的真实应变值不一致。

Pak[7]、Ansari[8]、高庆[9]、李东升[10]分别得出了具体结构实际应变和光纤传感器所测应变之间的传递率公式，但未仔细分析影响光纤光栅传感器应变传递的各种因素的具体影响。周广东[11]分析了粘贴层的弹性模量、泊松比、厚度及光纤光栅粘贴长度对传感器应变传递率的影响，但未涉及金属基底封装方式中基底尺寸参数对平均应变传递率的影响分析。本文结合已有的研究成果，推导出一种金属基底封装的表面粘贴式光纤光栅传感器的平均应变传递率公式，并详细分析了封装基底的长、宽、厚及其弹性模量对应变传递率的影响，为金属基底封装式光纤光栅传感器的设计提供了各种参数的参考。

1 光纤光栅传感原理

光纤光栅是在光纤纤芯上建立起一种空间周期性折射率分布，使其对特定波长的入射光具有反射作用，被反射光的中心波长称为布拉格波长。

当只有轴向力作用于光纤光栅且温度变化不大时，布拉格波长的漂移为

Δλε=(1-Pe)λBΔε

(1)

式中：Δλε为应变引起的中心波长漂移；Pe为光纤光栅的弹光系数；λB为光纤光栅的中心波长；Δε为应变的变化量[12]。

令1-Pe=Kε，Kε称为光纤光栅相对波长应变灵敏度系数，当选定光纤光栅后，Kε为定值。基于以上分析，光纤光栅中心波长的偏移量与轴向均匀应变呈线性关系。

2 光纤光栅传感器力学模型及平均应变传递率公式

光纤光栅金属基底封装传感器的纵向截面示意图和横向截面示意图分别如图1和图2所示。光纤光栅通过粘胶固定于刻有细槽的金属薄片上。粘贴长度为2L′，大于用作传感的栅格长度。光栅采用激光在光纤上刻写而成，其物理特性较光纤改变不大，可以将两者的弹性模量和几何尺寸做等同处理。封装基底的厚度和宽度分别为H、L；用于铺放光纤的凹槽，其横截面为正方形，边长为l；光纤光栅的半径为r1，光纤光栅下表面到基底之间的粘胶厚度为A，粘贴基底与被测结构的粘胶厚度为B。

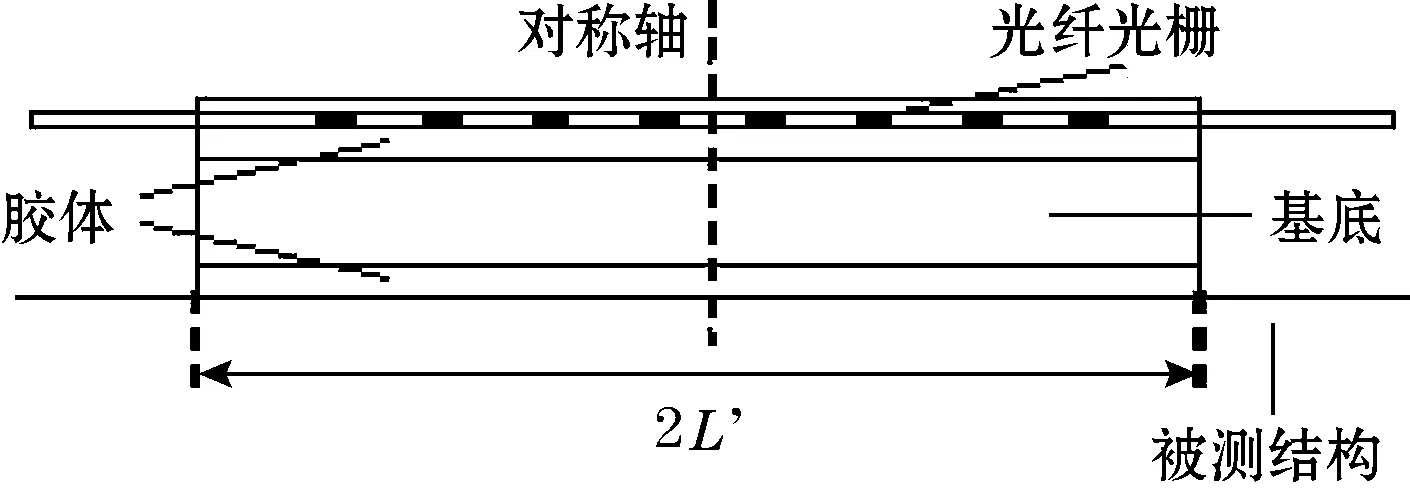
图1 纵向截面示意图

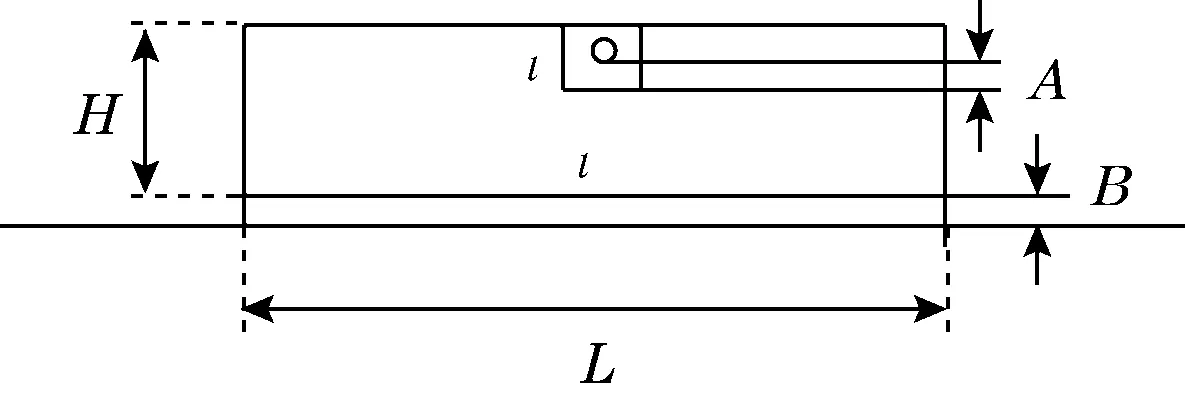
图2 横向截面示意图

应力分布示意图如图3所示。取图1中对称轴右侧的一半对其进行研究，对称轴上光纤光栅圆心处为x和y方向坐标原点，x轴沿光纤光栅轴向，y轴方向竖直向下。并从上到下对传感器的各部分进行编号。

图3 应力分布示意图

在分析中做如下假设，所有材料均为线弹性；被测结构沿光纤轴向均匀拉伸，并通过胶体4使基底产生形变，基底形变通过胶体2使光纤产生形变；传感器各部分之间接触良好，没有相对滑移；粘贴传感器后对被测结构没有影响，粘贴光纤光栅后对基底没有影响。

由图3，取基底3，胶体4所示的微元段为研究对象，此时忽略光纤光栅和胶体2对基底变形的影响。

联立基底3，胶体4的受力平衡方程和应力与应变关系式σ=Eε可得：

(2)

(3)

(4)

只考虑轴向变形，由弹塑性力学相关内容可得：

(5)

式中：u为胶体的轴向变形;G4为胶体4的剪切模量。

(6)

式中：y3为胶体4上表面与基底连接处的坐标值；y4为胶体4下表面与被测结构连接处的坐标值。

(7)

解方程(6)可得:

(8)

取光栅1，胶体2所示的微元段为研究对象，联立其受力平衡方程和应力与应变关系式σ=Eε可得：

(9)

(10)

故可得:

(11)

只考虑轴向变形，由弹塑性力学相关内容可得:

(12)

式中：G2为胶体2的剪切模量；y1为为胶体与光纤光栅下表面连接处的坐标值；y2为胶体2下表面与基底连接处的坐标值。

(13)

(14)

解方程(14)可得：

(15)

由式(8)和式(15)可得应变传递率公式为

(16)

(17)

3 应变传递影响因素分析

制作光纤光栅所用的光纤与普通光纤相同，各个厂家生产的光纤物理性质基本一致，所以对光纤光栅的半径和弹性模量不做讨论。平均应变传递率随着粘胶厚度的增加而减小，随着粘胶剪切模量的增加而增加，以下不再展开讨论。以下主要对基底的长、宽、厚及其弹性模量4个因素对平均应变传递率的影响进行详细分析。

表1给出了各种影响因素的默认值和待分析的4个影响因素的变化范围。当选定某个因素作为变化量时，其余因素的数值取默认值。

表1 影响因素默认值和变化范围

图4是当基底长度变化时，得到的平均应变传递率图形。从图4可以看出，基底越长，也就是光纤光栅的粘贴长度越长，平均应变传递率就越大。传感器基底长度要大于光纤光栅长度。而在制作传感器时，基底长度的变化可塑性较大，所以基底长度是改变传感器平均应变传递率的一个重要因素。但光纤光栅传感器所测得的应变值是粘贴部分的平均应变，如果长度太大，则测得的应变值不能很好地反映粘贴点的应变情况。所以，当不需要很精确地反映某一点的应变值时，可以通过增加基底长度来改变平均应变传递率，由图4可知，当基底半长为25 mm时，传递率达到0.67；当需要精确测量某点应变时，基底不应设计太长，此时应通过改变其他物理量来调节应变传递率。在实际生产中，可以根据不同的结构特征和测试要求来设计传感器的长度。

图4 基底一半长度对平均应变传递率的影响

图5为基底宽度与平均应变传递率的关系。从图5可以看出，平均应变传递率随着基底宽度的增加呈下降趋势，但变化不大。当基地宽度从5 mm变化到10 mm时，传递率减少0.008，可见基底宽度对传感器的平均应变传递率影响不大。但当粘贴宽度增大时，基底面积也会相应增大，从而会影响测量结果的精度。综合考虑基底宽度与平均应变传递率和基底粘贴面积与测量精度之间的关系，对于大多数的结构，基底宽度选择5 mm左右。

图5 基底宽度对平均应变传递率的影响

图6为基底厚度与平均应变传递率的关系。从图6可以看出，平均应变传递率随着基底的厚度增加而呈现下降趋势，且基底厚度对传感器的平均应变传递率影响较大。当基底厚度从0.8 mm增加到3 mm时，平均应变传递率从0.52下降到0.24。基底厚度是影响传感器传递率的另一个重要因素。在设计时，基底的厚度要大于所刻槽的深度，而刻槽深度取决于光纤光栅的直径。当选用的光纤光栅直径为0.27 mm时，在加工精度范围内应使槽深尽量接近这个数值，如加工为0.3 mm，此时的基底厚度应在加工能力范围内尽量接近0.3 mm，可以取0.4～0.5 mm。这样加工可以保证较高的平均应变传递率。而在结构应变较大时，应适当增加基底厚度来减小应变传递率，增大传感器的量程，从而保证结构形变范围在传感器量程之内。

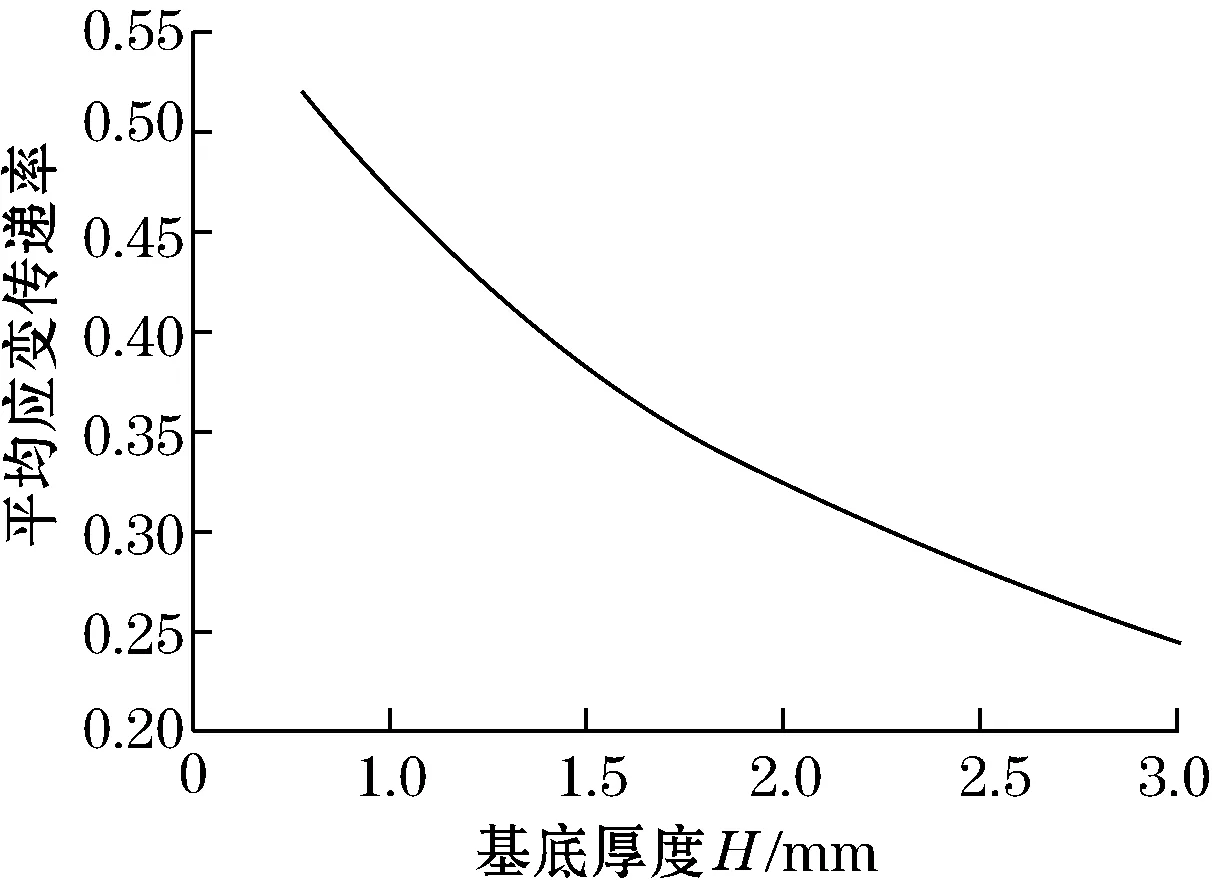
图6 基底厚度对平均应变传递率的影响

图7为基底弹性模量与平均应变传递率的关系。从图7可以看出，平均应变传递率随着基底材料弹性模量的增加而减小，当弹性模量从1×1010Pa增加到9×1010Pa时，平均应变传递率从0.76减小到0.42。设计尺寸一定时，可以通过选取不同材料的基底来灵活改变传感器平均应变传递率。当结构形变不大时可以选择弹性模量较小的基底材料，在满足量程的前提下提高传感器平均应变传递率；当测量大变形结构时，应选择弹性模量较大的基底材料，以增加传感器的量程，满足测量需要。

图7 基底弹性模量对平均应变传递率的影响

4 结论

本文推导出了一种基底封装式光纤光栅传感器的平均应变传递率公式，并通过对影响其平均应变传递率的4个基底参数分别进行分析，得出了一些结论，为生产和进一步研究提供参考。基底封装式光纤光栅传感器的平均应变传递率随着基底长度的增加而增加，随着基底的宽、厚和基底材料弹性模量的增加而减小。相比较，基底的宽度对平均应变传递率影响较小。所以，改变传感器的平均应变传递率应主要从基底的长度、厚度、基底材料3方面着手。当基底的各个尺寸已经确定时，可以通过改变基底材料的弹性模量来调整传感器的平均应变传递率。

以上分析结果是在所建模型基础上进行理论分析、公式推导和仿真得出，以后阶段还要对所得结果进行实验验证。

[1] 詹亚歌,蔡海文,耿建新,等.铝槽封装光纤光栅传感器的增敏特性研究.光子学报,2004(8):952-955.

[2] JONES S C,CIVJIAN S A.Application of fiber reinforced polymer overlays to extend steel fatigue life.Journal of Composites for Construction,2003,7(4):331-338.

[3] TAVAKKOLIZADEH M,SAADATMANESH H.Fatigue strength of steel girders strengthened with CFRP patch.Journal of Structural Engineering,2003,129(2):186-196.

[4] 胡曙阳,赵启大,何士雅,等.金属管封装光纤光栅用于建筑钢筋应变的测量.光电子·激光,2004(6):688-690.

[5] 于秀娟,余有龙,张敏,等.铜片封装光纤光栅传感器的应变和温度传感特性研究.光子学报,2006(9):1325-1328.

[6] 任亮,李宏男,胡志强,等.一种增敏型光纤光栅应变传感器的开发及应用.光电子·激光,2008(11):1437-1441.

[7] PAK Y E.Longitudinal shear transfer in fiber optic sensors.Smart Materials and Structures,1992(1):57-62.

[8] FARHAD A,YUAN L B.Mechanics of bond and interface shear transfer in optical fiber sensors.Journal of Engineering Mechanics,1998(4):385-394.

[9] 高庆,康国正.短纤维复合材料应力传递的修正剪滞理论.固体力学学报,2000,21(3):198-204.

[10] LI D S,LI H G.Strain transfer of fiber Bragg grating sensors.Optical Engineering,2006,45(2):402-409.

[11] 周广东,李宏男,任亮,等.光纤光栅传感器应变传递影响参数研究.工程力学,2007(6):169-173.

[12] 郑卜祥,宋永伦,张东生,等.光纤Bragg光栅温度和应变传感特性的试验研究.仪表技术与传感器,2008(11):12-15.

Strain Transfer Factor Analysis of Basal Grooving Encapsulating Fiber Bragg Grating Sensor

SHEN Hao-wen,ZHU Ping-yu,XU Pei-sheng,SHI Wei

(The Mechanical and Electrical Equipment Condition Monitoring and Control Municipal Key Laboratory of Guangzhou University,Guangzhou 510006,China)

Fiber Bragg grating(FBG)sensor was mostly pasted on the structure surface to measure the strain after encapsulating.However,as the existence of encapsulating basement and viscose,there were some deviations between real strain and FBG sensing value.The simplified strain transfer mechanics model of basal grooving encapsulating FBG sensor was established,and the corresponding average strain transfer ratio formula was deduced.The impact of length,width,thickness and elastic modulus of the base on the average strain transfer rate was analysed.The results show that within the effective range,the average strain transfer rate of basal grooving encapsulating FBG sensor increases with the rise of basement length,decreases with the growth of basement width,thickness and material elastic modulus,providing quantitative guidance for FBG grooving encapsulation.

fiber Bragg grating;strain;transfer rate;affecting factor;basement

国家自然科学基金资助项目(51105140)；广州市重点实验室资助项目(2060402)

2014-10-18 收修改稿日期：2014-12-06

TP212.14

A

1002-1841(2015)02-0096-04

申昊文(1989—)，硕士研究生，主要研究方向为力学分析、光纤光栅传感器的应用研究。E-mail:shentuomasi@163.com 朱萍玉(1971—)，教授，博士，从事光纤传感技术及应用、机电设备智能维护方面的教学和科研工作。 E-mail:pyzhu@gzhu.edu.cn