重基础 强通法 善应变——2015年1月浙江省学考第33题阅卷带来的启示

●沈金兴 (桐乡凤鸣高级中学 浙江桐乡 314500)

重基础 强通法 善应变
——2015年1月浙江省学考第33题阅卷带来的启示

●沈金兴 (桐乡凤鸣高级中学 浙江桐乡 314500)

2015年浙江省普通高中学业水平考试的阅卷工作已结束，笔者有幸担任了数学卷第33题(即解析几何这一题)的阅卷小组长.在阅卷过程中，笔者统计了该题的一些解题方法和错误类型，并从中获得了一些教学启示，在此与大家共享.

1 2种主要解法

1.1 原题呈现

题目已知点P(1，3)，Q(1，2).设过点P的动直线与抛物线y=x2交于点A，B，直线AQ，BQ与该抛物线的另一交点分别为C，D.记直线AB，CD的斜率分别为k1，k2.

1)当k1=0时，求弦AB的长.

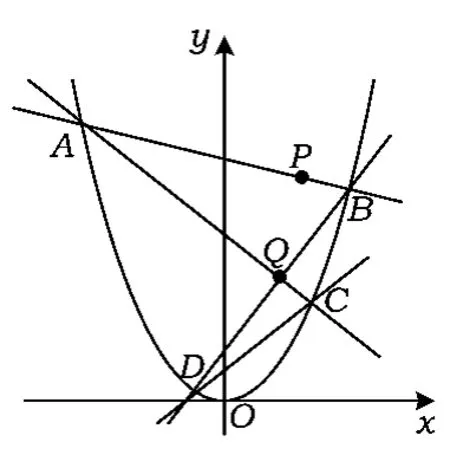
图1

2)当k1≠2时，是否为定值?若是，求出该定值;若不是，请说明理由.

1.2 解法总结

此题的解法较多，归纳一下，主要有2种(其余的解法大同小异，在思维本质上是类似的).

解法11)当k1=0时，直线AB与抛物线的交点为，故.

2)设直线AB的方程为y=k1(x－1)+3，设.联立方程组

解法1即为试卷所提供的参考答案，其中第1)小题满分为3分，第2)小题满分为5分.解法2相对繁琐一些，第1)小题是利用弦长公式，第2)小题是设直线方程求得.

解法21)设直线AB的方程为y=k1(x－1)+3，联立方程组，消去y得

以下过程与解法1相同(略).

这道题的主要解法就是这2种:设点和设直线方程，应该说都是“通性通法”.但就该题而言，解法1计算简便，解法2较繁杂，不易算对.

2 错误类型

2.1 错误类型归类

经过4天的阅卷，笔者发现学生在解答过程中的一些错误情况.本文借鉴了王光明教授等对数学解题错误的类型划分方法，把它们大致分成了4大类［1］.

1)第1类称为习惯性错误:就是学生在解答过程中，由于抄错、写错，看错题目数据、条件，或者到最后计算错误导致的答案不对.

2)第2类称为认知性错误:就是学生在解答过程中，公式记错或代错;知识点理解不到位，或者对题目理解错误等原因导致解题错误.

3)第3类称为逻辑性错误:就是学生在解题过程中，有一定思路，但思考不全面从而做不下去;或者把知道的一些零星知识点罗列在一起，思维混乱;或者书写紊乱，无法进行有效思考，从而得不出正确结论.

4)第4类称为策略性错误:就是学生解题时方法使用不恰当导致错误;或者学生面对题目时，不知从何下手，毫无解决问题的策略，即空白不答，或者纯粹乱写一气.

2.2 第1)小题的错误类型

第1)小题本来是容易的送分题，但也出现了各种各样的错误:

1)第1类是习惯性错误:有较多的学生犯这类错误，比如非常简单的一些计算错误，如x2=3⇒ x=±3;x2=3⇒x=9;;还有看错题目，把点Q(1，2)错当成点P，从而计算得.

2)第2类是认知性错误:如有学生把k1=0时的直线AB的方程写成y=1，从而算错交点;或者求k1=0时，不会用点P代入，而是得到直线方程y=b，从而不知如何算下去;或者采用了抛物线焦点弦的弦长公式，即学生没有弄清该公式的适用情况;或者在使用弦长公式时错用成“点到直线距离公式”等等.

3)第3类是策略性错误，主要表现在以下2种情况:①方法使用不当，如采用弦长公式来解题，但因步骤、计算较繁，从而导致结论错误;②空白不答，学生无能力解决此问题.

4)第4类是逻辑性错误:如学生把知道的一些公式乱写在一起就好了，不会应用，但此类错误总体上不多.

如果学校规模不大，班级人数较少，还可以采用“马蹄形（U型座）”“圆桌会议式”等排座方式。这些新型的排座方式都能最大限度地尊重个体需求，发挥互补合作的作用，促进新的学习模式的建立，也适合当前的教育主题——提高学生的核心素养。我们在编排座位时还应该坚持以下几点：

2.3 第2)小题的错误类型

第2)小题犯错误的学生更多，主要是以逻辑性错误与策略性错误为主.

在逻辑性错误中主要表现为:学生解此题有一定思路，但逻辑不完整，从而最后算不出结果，如有学生只算出k2=x3+x4，k1=x1+x2，代入后得

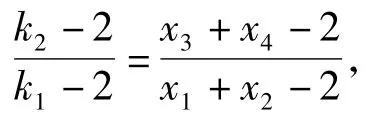
就算不下去了，或继续算到

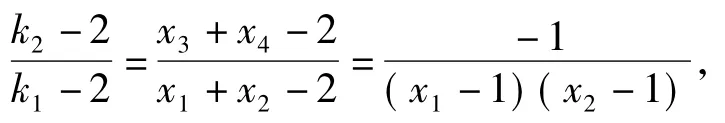
就不会算了，即缺少韦达定理的应用.

策略性错误主要体现在:1)方法使用不恰当，导致计算太繁，从而不能得出正确结论:如求直线AC，BD的方程时采用两点式，方程设得很繁，或者去求出2条直线AC，BD的交点，而不会用点Q去代;2)公式应用不合理:如联立成方程组后，消去y得一元二次方程，接下来不用韦达定理而是用求根公式，因太繁做不下去;3)空白不答或乱写一气:表明学生没有解决该问题的策略.

再是习惯性错误:学生在解此题时，思路、方法全对，但到最后算错，或者一开始直线方程写错，如把点P(1，3)当成了点P(1，1)或点P(3，3)等等.

认知性错误:学生在解题时代错公式，如斜率公式代错，或者直线方程与韦达定理用错等等.

3 数据统计

上面是从定性角度进行了错误类型的分析，接下来就从定量角度进行数据统计.

3.1 调查统计方法

为了弄清学生所犯的这些错误类型的百分比，笔者抽样调查了700份试卷(其中第33题满分的试卷除外).抽样中该题最高得7分(满分8分)，平均得分为3.67分，不到该题分值的一半，因此命题组很惊讶，抽样中竟有21.1%的人得0分.笔者有意识地多抽样了一些0分卷，想了解一下学生得0分的原因，为以后命题提供参考.

3.2 统计结果

为了方便了解，把解题中的错误类型所占的百分比的数据列表统计，见表1.

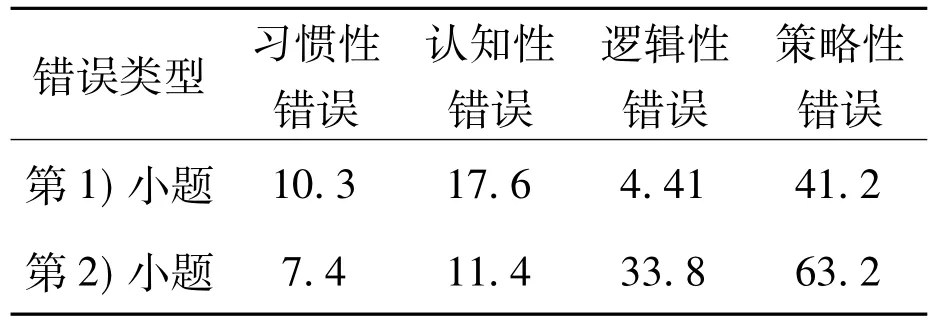
表1 学生在第33题中所犯的错误类型(数据为所占抽查样本的百分比)

从表1可知，第1)小题还是有一部分学生得到了满分，即3分.由于该小题比较简单，要么会做，要么不会做，故犯逻辑错误的较少，犯的最多的还是策略性错误.而第2)小题，有一些学生会犯下不止一个错误，如既犯了策略性错误中的方法不当，且同时又犯了认知性错误或逻辑性错误等，故第4类错误的百分比之和超过100%.

纵观整道题，学生犯的策略性错误最多，这与抽样调查了较多0分卷有关.因为在所抽样的所有0分卷中，第1)小题有67.8%的学生空白不答，第2)小题有90.3%的学生空白不答.另外得0分的原因是学生乱写一气，2个小题分别占12.9%与9.7%.乱写一气是指学生随便写一些数据、公式或其他的字，最终答案不对，表明这类学生还是没有任何解决该题的正确策略，故仍归为策略性错误，而非逻辑性错误.

当然，参加这次学业水平考试的许多学生是上次学考没有通过的，故程度普遍较差一些，这也是得分不高的原因之一.

4 教学启示

通过对学生错误类型的分析和统计，可以为以后的教学带来一些启示，尤其是对学业水平考试的复习，更具有针对性和方向性.

1)重视基础.不管是学业考试还是高考，都有一些基础题，尤其是学业水平考试，更是如此.而重视基础，不仅是要把基本知识、基本概念理解深刻，更要掌握解题的基本技能，即打好“双基”.如这道解析几何题，第1)小题本该是送分题，却有许多学生犯了认知性错误，甚至有的学生空白不答，说明连最基本的解题方法也没有掌握.

2)强调通法.在解题教学中，强调“通性通法”应该是永远不变的主旋律，因为不管大题还是小题，通用方法都能解决问题.比如解析几何题，联立方程组消元后，应用韦达定理来解题是最基本的策略，务必要让每个学生掌握.章建跃博士说:“通性通法”才是解题之大道，因此作为一线教师，一定要多强调通法，而不是炫耀技巧.

3)善于应变.在夯实基础、学会通法的同时，还要学会应变.据命题组组长说:当时命题时，第1)小题本是送分的，可考出来的结果让人大跌眼镜.原因是多种多样的:有算错的，有看错的，还有用“弦长公式”来算因繁杂而出错的，也有认知错误的，乱写的等等.这也表明一些学生不能随机应变，反而把简单的策略遗忘掉.这也是教师在教学中要注意的问题，即要注重变式教学，训练不能太僵化，要善于应变.

4)提高计算力.在阅卷中，有相当多的学生由于计算错误而导致失分，有的甚至到了最后一步还算错，这说明现在学生的计算能力还较差，习惯性错误犯得较多.这也提醒教师在平时的教学中，除了培养学生的逻辑推理能力外还要提高学生的计算能力，把不该犯的错误降到最低.

［1］ 王富英，王光明，魏荣芳.“错误重复现象”产生的原因及消除对策［J］.数学通报，2011 (7):18-21.