近几年活跃在高考中的二次函数绝对值问题探究

●何官勇 (鲁迅中学柯桥校区 浙江绍兴 312028)

近几年活跃在高考中的二次函数绝对值问题探究

●何官勇 (鲁迅中学柯桥校区 浙江绍兴 312028)

绝对值是中学数学中的一个重要概念，贯穿于整个中学数学教学之中.综观近几年全国各地的数学高考试卷，可以发现“绝对值与二次函数结合的问题”备受命题者青睐.因其不仅具有绝对值本身“起点低、入手易”的特点，更能体现学生对函数综合问题的处理能力，是考查转化化归、数形结合与分类讨论思想的好素材.笔者将对二次函数绝对值问题作一些探讨.

1 形如f(x)=|ax2+bx+c|或f(x)=a|x|2+ b|x|+c(其中a不为0)问题探究

这是高中数学教学中的一类基本问题，其图像可由图像翻折变换或者绝对值零点正负讨论得到，这里不再赘述.

解决此类问题的基本策略:

1)作出函数图像，结合图像并比较图像之间的关系，往往需要关注单调区间的转折点与定义域区间的关系;

2)若题中含参数，则分类讨论解题.

例1已知函数f(x)=x2+ax+1，其中a∈R，且a≠0.

1)若f(x)的最小值为－1，求a的值;

2)求y=|f(x)|在区间［0，|a|］上的最大值;

3)若方程|f(x)|=x－1在区间(0，+∞)上有2个不相等实根，求a的取值范围.

(2015年浙江省绍兴市高三期末考试试题)分析 第1)小题考查二次函数的基本问题，易得而第2)和第3)小题重点考查函数y=|f(x)|的图像问题，运用数形结合较容易得到解答.对于第2)小题，因为f(0)=1＞0，所以只需要比较f(0)，，f(|a|)之间的大小即可.解得

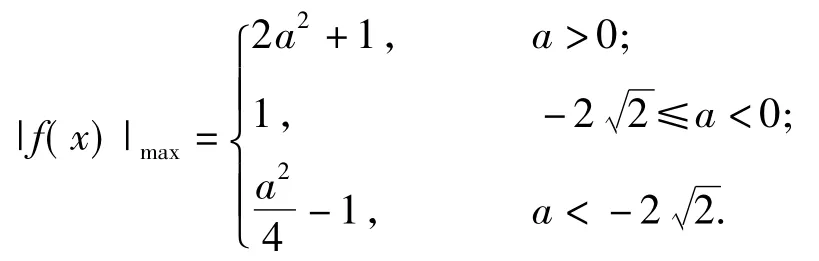
对于第3)小题，只需要考虑函数y=|f(x)|与函数y=x－1的图像交点关系:当a＞0时，如图1可得2个函数没有交点;当，即－2≤a＜0时，结合图2，可得;当 a＜－2时，结合图3，可得必满足题意.

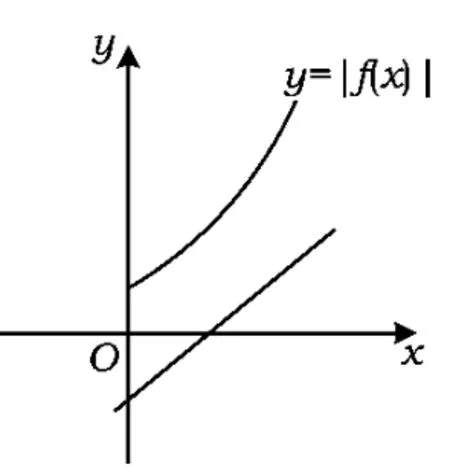
图1

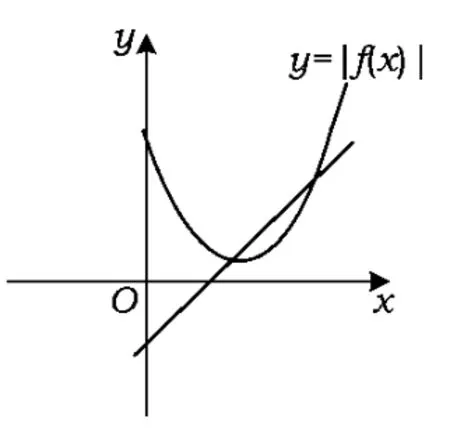
图2

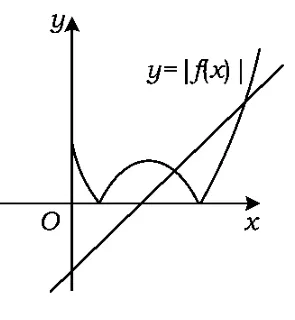
图3

2 形如f(x)=m(x－b)|x－a|+qx+t(其中m不为0)问题探究

这是一类局部绝对值问题，是目前试题中经常出现的题型.其本质是分段函数，且其中一段开口向上，另一段开口向下.我们先研究这类函数图像，原函数可转化为

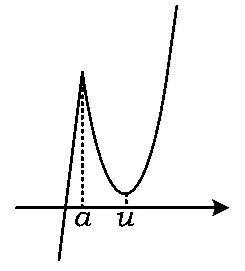
图4

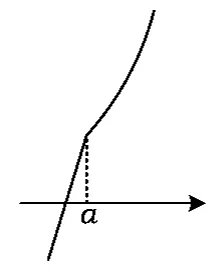
图5

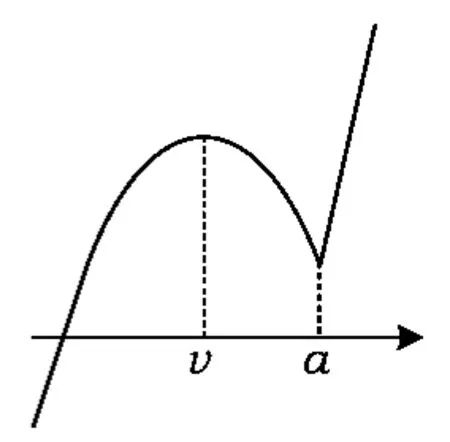
图6

情形2若q=0，可得u=v，即分段函数对称轴相等.此时函数图像转化为:

①当a＞b时，如图7所示;

②当a≤b时，如图8所示.

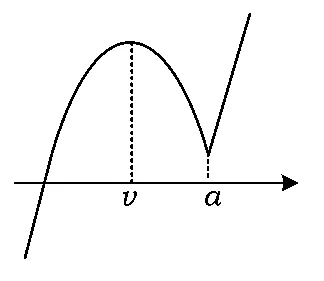
图7

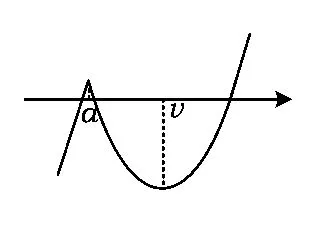
图8

情形3若m＞0，q＜0，则讨论图像时，只需将对称轴u，v的位置交换，再作图即可.

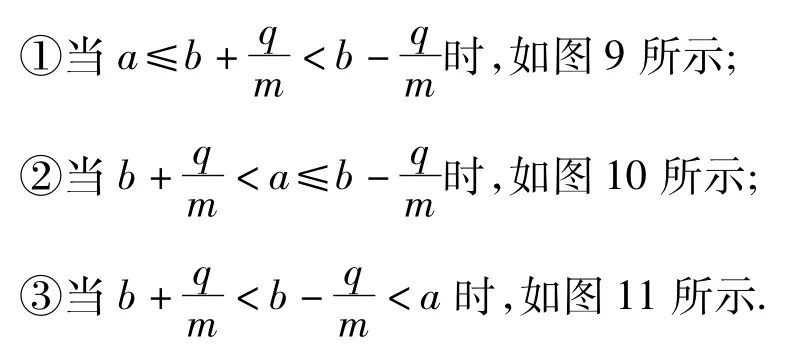
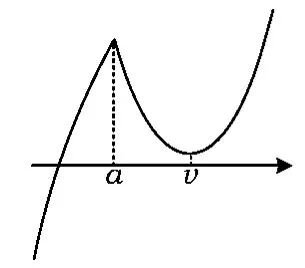
图9

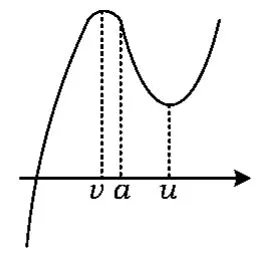
图10

图11

情形4若m＜0，则讨论方式与上述情形一样，只需要开口方向向上换成向下即可(此处不再探究).

由上述分析，可得此类图像可能的单调区间为1个或3个，解题基本策略:

1)比较分段函数的2条对称轴与绝对值零点之间的关系;

2)确定函数类型，弄清属于哪种图像，有1个还是3个单调区间，以及相应的单调区间转折点;

3)比较函数图像的几个单调性转折点与所给函数定义域端点之间的位置关系，若题中带有参数，则进行参数讨论.

例2已知函数f(x)=x|x－a|+2x.若存在a∈［0，4］，使得关于x的方程f(x)=tf(a)有3个不相等的实数根，则实数t的取值范围是 ( )

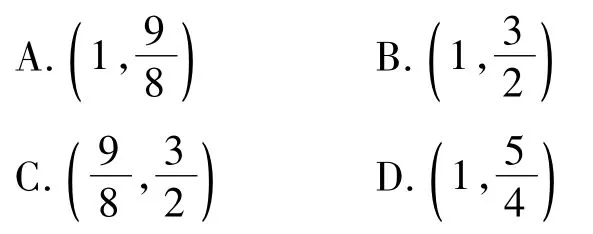
(2015年浙江省杭州市学军中学模拟题)

分析由题意知，

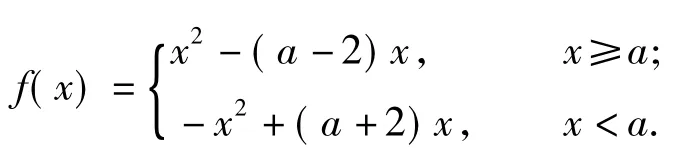
例3已知函数f(x)=|x－m|和函数g(x)= x|x－m|+m2－7m.若对任意的x1∈(－∞，4］，均存在x2∈(3，+∞］使得f(x1)＞g(x2)成立，求实数m的取值范围.

分析本题函数g(x)的图像同情形2，结合图像即可分析得出g(x)的最小值

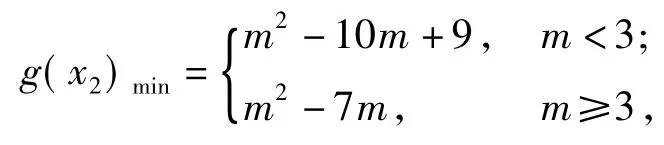
3 形如f(x)=|ax2+bx+c|+qx+t(其中a＞0)问题探究

这是一类二次函数整体放在绝对值内的问题.若b2－4ac≤0，则f(x)=ax2+bx+c+qx+t，是二次函数问题，这里不作研究.当b2－4ac＞0时，记，下面对该类问题的图像进行讨论:原函数可转化为

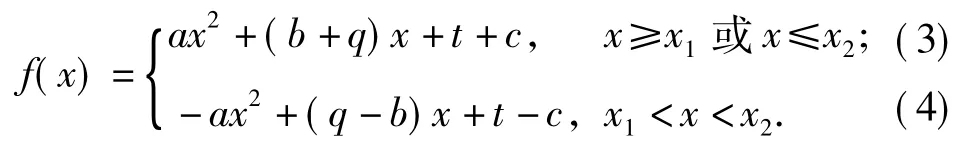
该函数是分段函数，其中一段开口向上，另一段开口向下.对称轴分别为，原题转化为讨论分段二次函数的对称轴与定义域分割点x1，x2之间的关系解决.

情形1为了便于讨论，先考虑q＞0的情形.分析可得u＜v，x1＜v且u＜x2.若，则u≤x1＜x2≤v，如图12所示;若，则x1≤u＜v≤x2，如图13所示.

式中:α为归一化的反应进程;A为指前因子;n为反应级数;E为活化能;R为理想气体常数;t为反应时间,T为样品温度。在绝热追踪阶段,当环境温度和样品温度时刻相等时,满足样品反应自放热完全用于系统温度升高的条件,则可得到热平衡方程:

图12

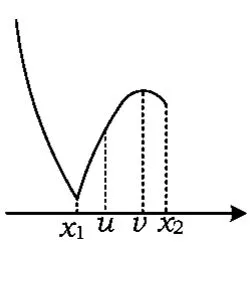
图13

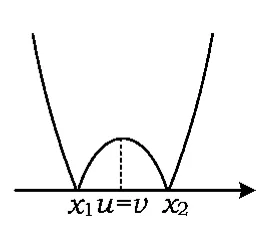
图14

情形2若q=0，可得u=v，即分段函数对称轴相等，即x1＜u=v＜x2，如图14所示.

情形3若q＜0，讨论图像时，只需将对称轴u，v的位置交换，再作图即可.

由上述分析，可得这类图像可能的单调区间为2个或4个，解题基本策略:

1)判断绝对值内二次函数值是否恒大于等于0;

2)若绝对值内的二次函数有2个零点，则比较分段函数的2条对称轴与绝对值内二次函数2个零点之间的关系;

3)确定函数类型，弄清楚属于哪种图像，有2个还是4个单调区间，以及相应的单调区间转折点;

4)比较函数图像的几个单调性转折点与所给函数定义域端点之间的位置关系，若题中带有参数，则进行参数讨论.

例4已知函数f(x)=|a2x2－1|+ax(其中a∈R，且a≠0).

2)当x∈［－1，1］时，求函数y=f(x)(其中a＜0)的最大值M(a).

(2015年浙江省丽水市高考模拟题)

分析第1)小题可转化为函数f(x)=|a2x2－1|+ax的图像与直线y=c的交点问题，由上述图像探究，可得图15.

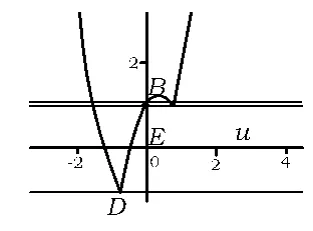
图15

第2)小题中，

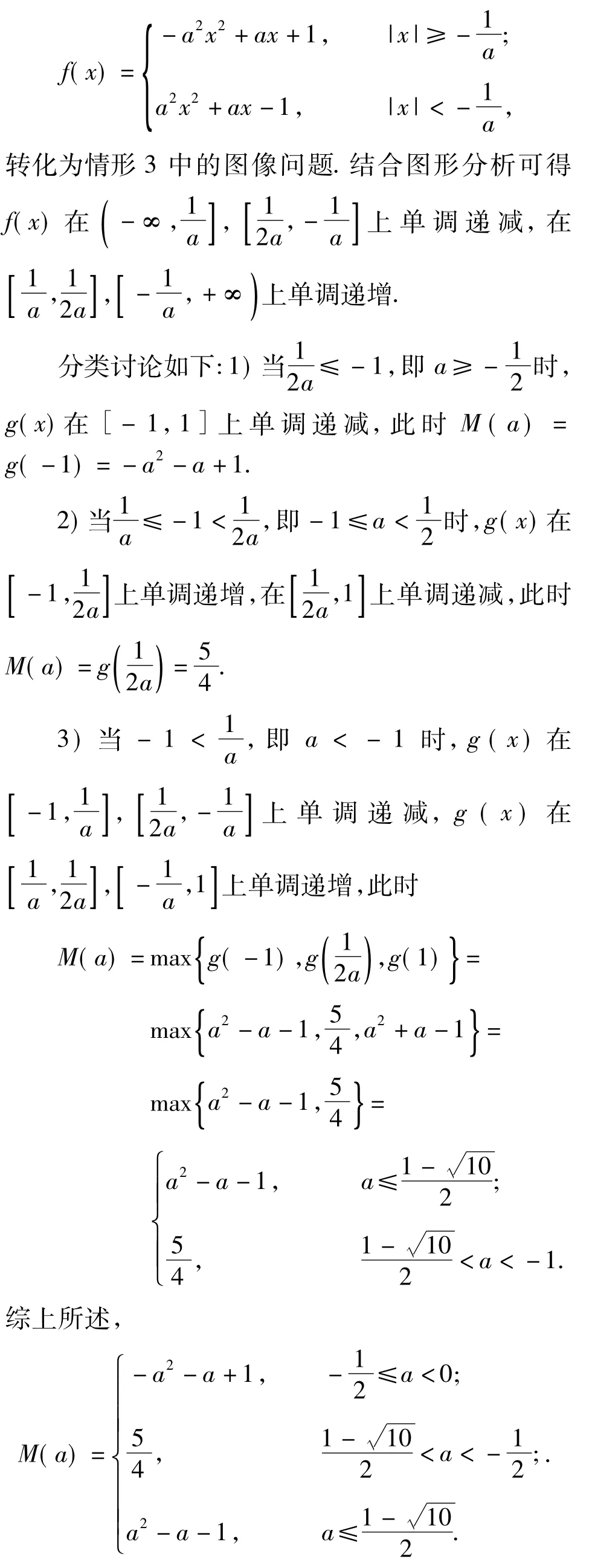
4 其他常考问题

形如f(x)=m(x－b)|x－a|+px2+qx+t，f(x)=|ax2+bx+c|+px2+qx+t，f(x)=|ax2+ bx+c|+|px2+qx+t|等问题.

此类问题与前2类问题相比较，区别在于二次项系数可能出现同正、同负、一正一负或0的情形，这里图像问题不再作讨论，其讨论思路可类比前2类讨论.此类问题的解题基本策略:

1)对绝对值进行零点讨论，写出分段函数的表达式;

2)确定分段函数的对称轴，比较对称轴与零点之间的关系，作出函数图像;

3)数形结合，讨论解题.

例5设 a为实数，函数 f(x)=2x2+(xa)|x－a|，求f(x)的最小值.

分析原函数可化为

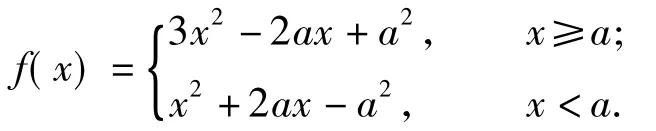
显然二次项系数均大于0，按对称轴与分段零点a之间的关系讨论，可得

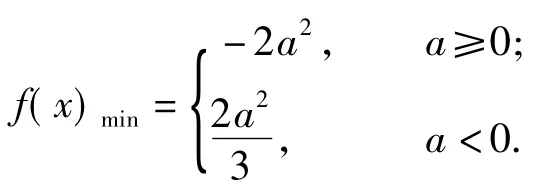
例6已知函数f(x)=x2－1，g(x)=a|x－1|.求函数h(x)=|f(x)|+g(x)在区间［－2，2］上的最大值.

(2015年浙江省杭州市第二中学高考模拟试题)

分析本题是带有双绝对值问题，可按零点讨论，化函数如下

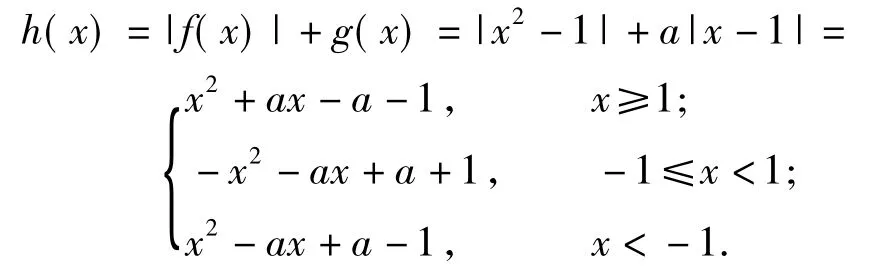
通过分析比较对称轴，与分段零点1，－1及区间端点－2，2之间的关系，结合图像讨论可得:当a≥0时，h(x)在［－2，2］上的最大值为3a+3;当－3≤a＜0时，h(x)在［－2，2］上的最大值为a+3;当a＜－3时，h(x)在［－2，2］上的最大值为0.

绝对值与函数结合是高考的热点与难点之一，尤其是二次函数绝对值问题，常常作为压轴题型出现.对这类问题的处理，如果能准确地掌握其图像特点，结合图像进行分类讨论，往往能起到事半功倍的效果.当然有时直接作图、含参讨论比较困难时，还可以考虑分离参数等方法解题.