品赏美发现妙追求境

陈少萍

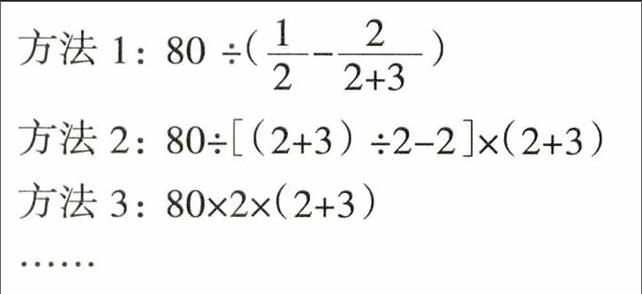
摘 要：数学的美是一种理性的美，教师应当积极引领学生以审美的眼光学习数学，努力做到感悟经验积累的过程美，力现学习探索之奥妙；欣赏数学公式的简洁美，显现模型建构之美妙；感受数形结合的奇巧美，体现几何直观之精妙；品赏思维灵动的智慧美，展现创新发展之绝妙，从而追求品质学习的境界。

关键词：数学美；过程美；简洁美；奇巧美；智慧美

中图分类号：G623.5 文献标识码：A 文章编号：1009-010X（2015）08-0071-03

数学是研究空间形式与数量关系的一门科学。数学的真表征着数学的科学价值，数学的善表征着数学的社会价值，数学的美则表征着数学的艺术价值。数学的美是一种理性的美，数学美具有在语言、体系、结构、模式、形式、思维、方法、创新理论等各方面的丰富表现形式。但是，在实际教学中，数学美的意蕴并没有被教师充分发掘，学生学得被动而缺乏情趣，缺少审美心态而呈现学习低效现象。 因此，教师应当引领学生欣赏数学所特有的“美”，以美激趣、以美融情、以美启智，这必将给数学教学改革注入新的活力。

一、感悟经验积累的过程美，力现学习探索之奥妙

在新课改的背景下，数学学科强调”四基”教学，突出数学活动经验的积累。数学活动既有学生物质化的直接活动，也有展现思维的间接活动，其活动过程有利于学生暴露思维、张扬个性。数学学习就其本质而言，首先应该在于让学生体验数学学习的探索过程，在丰富而又生动的活动中发现学习之奥妙。

教学“梯形的面积计算”时，教师为了让学生经历公式的探索过程，积累丰富的经验，按照方案拟定、验证并得出结论的过程，引领学生积极探索。在小组交流中，学生的探究思路多种多样，有的认为可以转化为长方形，也有的认为可以转化为平行四边形或是三角形进行研究。在操作活动中，各小组成员充分发挥聪明才智，有的借助剪一剪、拼一拼的方法，有的采用旋转和平移的方法，将梯形进行了图形转化，学生踊跃展示研究成果，并且在比较中发现：有的转化前后面积不变；有的是用两个完全一样的梯形拼成了平行四边形，梯形的面积是拼成的平行四边形面积的一半。在探索过程中，学生欣赏着一幅幅组拼的图形，经历着转化、比较、推理、发现等活动，自主推导出面积计算公式，此时此刻，一种审美和成功的愉悦油然而生。

从上面的例子可以看出，学生在活动中积累了动手操作、方法运用和转化策略等经验，在体验中感受到一种美的存在，这样的活动是一种“审美”。

二、欣赏数学公式的简洁美，显现模型建构之美妙

数学学科具有一定的抽象性、符号性。比如，数学中的公式很多，这些公式通常是经过一个由繁到简的模型构建过程，并通过比较、概括推导出来的。一些公式呈现非常简洁的形式，给学生以强烈的形式美，显现出模型建构的美妙之处！比如，圆的面积计算公式是s=πr2；长方体、圆柱体的体积计算公式统一为v=sh；这些公式如此简洁，给学生以审美的愉悦！

在运用已有知识解决数学问题，构建具体模型时，教师可以引导学生尝试寻求“化繁为简”的路径，追求“至简”境界。

我曾在教学中让学生探索“已知圆柱的底面半径r和高h，求表面积计算方法”，学生通常写出：

S=2πr2 +2πrh

教师启迪学生观察：在上面的方法中，是不是显得繁琐，能不能设法变得更简洁一些呢？学生运用乘法分配律进行了下面的变化：

S=2πr（r+h）

教师再次提问：如果一个圆柱的底面半径和高相等，求圆柱的表面积，你还能得到一个怎样的公式呢？

S=2πr（r+h）= 2πr（r+r）= 2πr×2r=4πr2（学生惊奇！正好是底面积的4倍呀！）

可见，许多解决问题的模型都可以简化其结构，使之更加简洁，更具有数学之美！同时，学生也初步构建了数学符号化思想和代数思想，感受到解题模型因符号而简洁，而更具形式美。

三、感受数形结合的奇巧美，体现几何直观之精妙

我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”。数和形是两个最主要的研究对象，它们之间有着十分密切的联系，在一定条件下，数和形之间可以相互转化，相互渗透。可以说，数形结合在小学数学教学中无处不在， 学生总会感悟到一种方法的奇巧之美！

一位教师在数学活动课上出了这样几道题：

1+3=

1+3+5=

1+3+5+7=

……

1+3+5+7+……+99=

学生开始算，但越算越麻烦，能不能有一种简洁的方法呢？

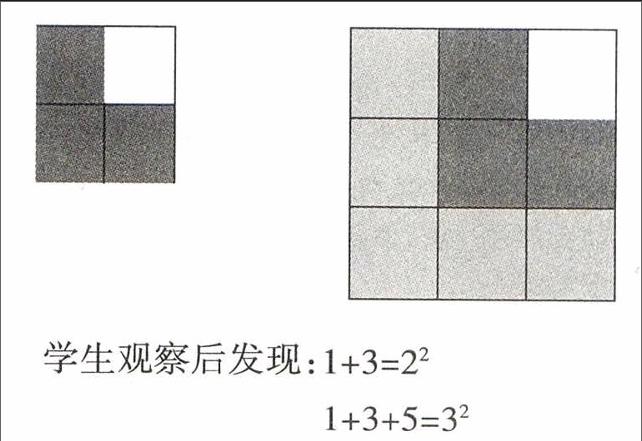
借助多媒体，教师出示了下列图示：

学生观察后发现：1+3=22

1+3+5=32

可以发现，这些题目的共同特点是：求从1开始的连续奇数的和。学生一般采用直接计算的方法，当个数越来越多时，直接计算已经越来越不方便，这时，教师巧妙地借助直观图示让学生一下子捕捉到解决问题的方法。图（1）是1个小正方形（假设边长为1）与3个同样的小正方形拼成一个边长为2的正方形；图（2）是1个小正方形、3个同样的小正方形与5个同样的小正方形拼成了一个边长为3的大正方形；很显然， 1+3+5+7+……99就可以转化为求拼成的正方形中包含着多少个小正方形的个数，正方形的边长是可以这样算的：

（1+99）÷ 2=50，502=2500

借助数形结合，学生惊奇地发现：借助图形可以非常直观地显示出简便的思路，快速算出结果。为了让学生更深刻地感受数形结合的奇巧之美，教师又编拟了下面的题目：

7+9+11……+99=？

学生观察后发现，这些数虽然是连续的奇数相加，但相加的数不是从1开始，他们的思维卡壳了，正方形不能直接构造出来，能不能借助几何直观巧妙解决问题呢？学生进行了小组交流，有学生闪烁出创造的火花：先构造出表示 1+3+5的正方形（32），再构造表示1+3+5+7+……+99（502）的正方形（图略）， 502-32 =2491，这是多么简洁的方法！

数形结合应用广泛，几何直观构思精巧，学生因此而建立正确表象，并能够借助表象深层次思考问题，数形结合的奇巧美与学生的认知情感有机融合，促进了学习活动的深入和问题解决的纵深发展。

四、品赏思维灵动的智慧美，展现创新发展之绝妙

数学教学的核心在于发展学生的思维，让学生思维更加灵动，时时处处展现智慧之美，不断活跃解决问题的思路并勇于创造，这必将展现学生创新发展的无比绝妙！

比如，教学这样一道题：

两车同时从甲、乙两地相向而行，当行到离中点80千米时两车相遇，这时慢车与快车所行路程的比是2：3，求全程。

教师要启迪学生用不同的方法灵活解决问题，从而发展能力。

方法2： 80÷[（2+3） ÷2-2]×（2+3）

方法3： 80×2×（2+3）

……

方法1中，学生在于想方设法找准80千米对应的分率，即80千米占全长的几分之几。

方法2 中，学生设法先求1份是多少千米，再将全程看作这样的5份，从而求出全程。

方法3尤其巧妙，如果把相遇时快车比慢车多行的路程看作 1份，这样的1份正好是2个80千米，再求这样的5份，这种方法很有创造性。

余文森教授在《有效教学十讲》中说，从能力的角度来说，创新性主要表现为求异思维、发散思维。在谈到发散思维的基本特征之一“变通性”时，突出了“思考能变换角度，不限于某一个方面，能提出各种不同的解决问题的办法，富有迂回变化的思路等等。”而不同的解决问题思路所蕴含的智慧，让学生感受到一种思路灵动的智慧之美，产生了数学学习的智趣。

总之，数学学习不仅是一种思维发展、素质提升的过程，同时也是一种审美的过程，只有立足于审美，体悟其美妙， 追求审美境界，数学教学方能凸现应有的价值，学习活动也才能向高层次、高品位方向发展，达成品质学习、高效学习的境界。

参考文献：

[1]余文森.有效教学十讲[M].上海：华东师范大学出版社，2009.