基于BP神经网络的房地产业上市公司财务绩效评价模型研究

王娟 杨雪

摘 要：本文以30家房地产业上市公司为研究对象，以净资产收益率、市盈率等6项指标为评价指标，在matlab环境下构建了基于BP神经网络的财务绩效评价模型，并对模型进行了优化和验证。实验表明，所建模型克服了传统财务评价方法的局限性，在既定条件下具有很好的适用性和动态性。

关键词：BP神经网络;财务绩效评价;房地产;上市公司

一、引言

对上市公司财务绩效进行传统的人工评价难以摆脱人为因素和模糊随机性的影响，进而影响到评价的客观性、准确性。建立适合的BP神经网络财务绩效评价模型不仅能够减少人为因素的影响，其所使用的非线性函数更贴近于复杂的非线性动态经济系统，比人工评价更具有适用性[1]。

二、模型构建与成型

（一）BP神经网络结构分析

1989年Robert Hecht–Nielson证明了对于任何在闭区间的一个连续函数都可以用具有1个隐含层的BP网络来逼近，因而一个3层的BP网络可以完成任意的N维到M维的映射，所以本文先采用3层BP神经网络来建立评价模型。

（二）指标选取与无量纲化处理

1.评价指标选取。房地产业上市公司开发周期长，投资大，受中央和地方政府政策影响大，这些特点都要求房地产业上市公司具有良好的盈利能力。因此，本文建立了以盈利能力为重点的财务绩效评价指标体系。该体系包括反映盈利能力的净资产收益率、主营业务成本率和市盈率，以及反映其他三项能力的基本指标资产负债率、存货周转率、主营业务收入增长率。

2.指标无量纲化处理。本文选择极差法[2]对财务绩效评价指标进行无量纲化处理。首先，将六项指标分为三类，分别为正向型指标：净资产收益率、存货周转率（由于所有样本的存货周转率都小于1，可以判断为越大越好）、主营业务收入增长率;负向型指标：主营业务成本率;区间型指标：资产负债率（最优区间为60%-70%）、市盈率（最优区间为14-20），然后，用matlab语句对正向型指标和负向型指标进行处理，对区间型指标的处理采用for循环语句和matlab条件语句来实现。

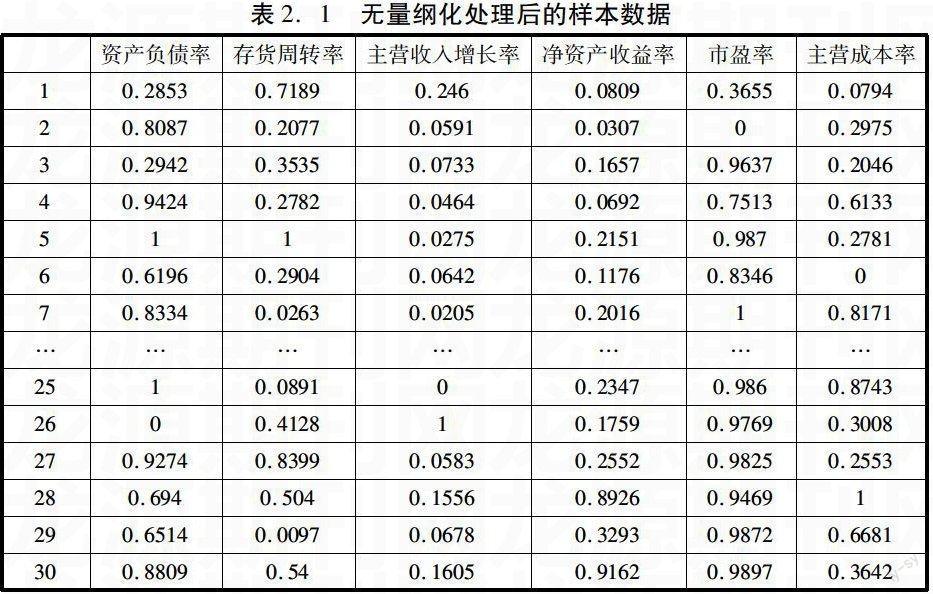
经过无量纲化处理，30个样本的财务指标数据如表2.1所示：

表2.1 无量纲化处理后的样本数据

资产负债率 存货周转率 主营收入增长率 净资产收益率 市盈率 主营成本率

1 0.2853 0.7189 0.246 0.0809 0.3655 0.0794

2 0.8087 0.2077 0.0591 0.0307 0 0.2975

3 0.2942 0.3535 0.0733 0.1657 0.9637 0.2046

4 0.9424 0.2782 0.0464 0.0692 0.7513 0.6133

5 1 1 0.0275 0.2151 0.987 0.2781

6 0.6196 0.2904 0.0642 0.1176 0.8346 0

7 0.8334 0.0263 0.0205 0.2016 1 0.8171

… … … … … … …

25 1 0.0891 0 0.2347 0.986 0.8743

26 0 0.4128 1 0.1759 0.9769 0.3008

27 0.9274 0.8399 0.0583 0.2552 0.9825 0.2553

28 0.694 0.504 0.1556 0.8926 0.9469 1

29 0.6514 0.0097 0.0678 0.3293 0.9872 0.6681

30 0.8809 0.54 0.1605 0.9162 0.9897 0.3642

（三）模型訓练与成型

笔者邀请专家按照相同的思维和判断对30个样本数据进行了评分，然后将前20组数据作为训练样本，后10组作为测试样本。本文用newff函数激活网络，选择能够将输出控制在[0-1]的tansig函数作为传递函数，将允许误差设为le-5，最大训练次数设为50000次，学习速率设为0.01，初始权值和阈值由网络随机生成。在实验中，将前20组样本数据以6行20列的矩阵形式作为输入值，再分别以traingdx、trainlm、trainbfg、traingd、traingdm等5种不同的训练函数和3到13的隐含层单元数进行学习，训练后用10组训练样本数据进行验证，各种不同组合得到的输出值与测试数据对应的期望值的平均相对误差。

实验发现，当以traingd和traingdm为训练函数时，不论隐含层为多少，均不能在训练50000次之内达到允许的误差le-5，因此表2.2没有列出其对应误差平均数。在以traingdx、trainlm和trainbfg为训练函数时，均可以在训练次数内达到允许误差。

当训练函数为trainbfg，隐含层单元数为3时得到的输出值与期望值的趋势最为接近，据表2.2又知，这种组合的相对误差平均值为1.71%，是4种组合中最小的，我们就将评价模型的训练函数确定为trainbfg，隐含层单元数确定为3个，这样评价模型就基本成型了，是一个6-3-1的BP神经网络模型。

三、模型优化与定型

以上成型的网络模型用于房地产业上市公司的财务绩效评价能够将误差控制在1.71%左右，但是财务绩效评价对误差的要求是越小越好，为得到更准确的评价，本文从改变传递函数、调整精度要求、增加隐含层数三个方面进行了探索，对这个模型作了进一步优化，结果如下。

改变传递函数：由于传递函数属性的差异，更改传递函数使得输出值溢出[0-1]的可能大大增加，得到更小的相对误差平均值都源于局部最优的结果。

调整精度要求：使得网络的收敛速度发生变化，但对改进输出值的准确性影响很小。

增加隐含层数：增加1个隐含层，新增隐含层单元数与原有隐含层单元数越接近越好，我们将其确定为3个单元数，这样就将原有模型拓展为4层网络，然后对新网络进行训练，再用测试样本测试。数据表明，增加隐含层进一步提高了模型的预测精度，平均相对误差由1.71%降为1.28%，对每个测试样本的相对误差也没有出现局部最优的情况。

人们在运用BP神经网络进行经济评价时，往往默认地使用3层网络，认为没有必要使用双隐含层网络，这种思路并不是完全正确的，神经网络隐含层数的确定需要具体问题具体分析，比如本文建立的双隐含层模型就可以获得比单隐含层模型更精确的结果。

为体现双隐含层模型的效果，本文再用1个新样本对该模型进行二次验证。新样本的6个指标分别为0.53、0.26、0.46、0.13、39、0.46，专家打分为0.5475，用优化后的模型进行评价，得到的输出值为0.5461，相对误差仅为0.2561%，增加隐含层提高精度的作用得以证实。本文运用BP神经网络对房地产业上市公司财务绩效进行评价的模型就最终定型了，是一个6-3-3-1形式的双隐层网络模型。

BP神经网络模型一经训练结束，就有固定的权值和阈值。训练好的net经保存就可以在以后任何时候调用，调用时会具备已经学习的能力。如果不保存net，在代码相同的情况下，只要以已有的权值和阈值进行初始化，也能得到相同的評价结果。

四、总结

本文从房地产业上市公司的特点出发，确立了以盈利能力为重点的财务绩效评价指标体系，采用极差法对样本数据进行无量纲化处理，建立了6-3-3-1形式的BP神经网络评价模型，克服了传统方法受人为和随机因素影响的缺点，能够对房地产业上市公司财务绩效进行有效评价，本文进行的二次验证表明，该模型具有较强的动态性，能够有效应用于同行业其他公司的评价。（作者单位：西南石油大学经济管理学院）

项目资助：西南石油大学开放实验基金资助

参考文献：

[1] 杜栋，庞庆华等.现代综合评价方法与案例精选[M].第2版.北京：清华大学出版社，2008：102-104.

[2] 于鹏飞，王丽娜.财务预警中样本数据无量纲化方法的选择[J].会计之友，2005（12）：43-44.