应用几何画板进行探究式学习

陈薛琴

【摘要】本文以用“几何画板”探求点的轨迹问题为切入点，论述用“几何画板”进行探究式学习。这种数学学习的步骤是：从实例出发——用“几何画板”进行实验操作——分析验证、发现规律——提出猜想、假设——进行证明——再进一步探究拓展。

【关键词】探究式学习 几何画板 点的轨迹

利用几何画板“探求点的轨迹教学”可以在教师的指导下，让学生独立或分组进行观察和分析，不必用“教师讲学生听”的传统教学方式进行。实现了即充分发挥教师的主导作用、又使学生成为学习主体的效果，是一个让学生自主进行探究式学习的直观环境，创造出了一种新型的探究式学习课堂教学模式。“促进有效学习”的课堂变革。

问题是思维的起点，是学生主动进行探索的动力，我们先来看一个具体的问题。

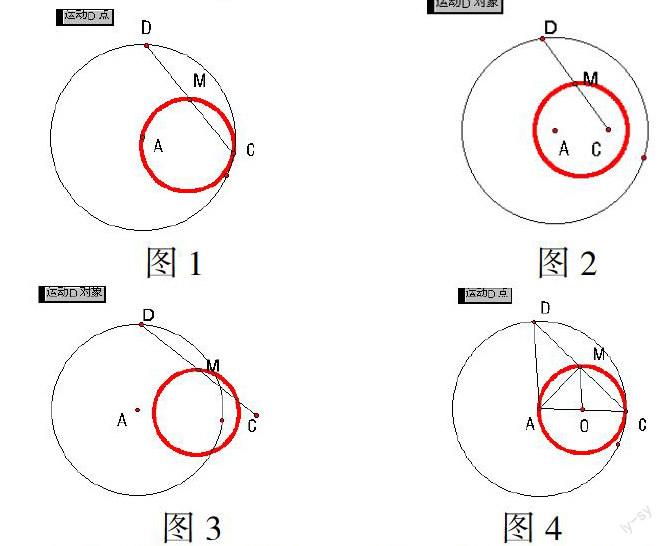
问题：D是圆A上的动点，C是圆A上的一个定点，问线段CD的中点M的轨迹是什么图形？

[进行实验操作]用几何画板进行探究中点M的轨迹

探究1：拖动点C使它分别位于圆A内部，圆A外部，此时，CD中点M的轨迹分别是什么图形？

[发现规律]点M的轨迹均为圆如（图1-4）。

[提出猜测]这些轨迹是不是半径相等的圆！

[从感性上升到理性]

由学生集体讨论分析为什么？观察几何性质，寻找几何关系，进行合情推理，并证明你的结论。

证明：取AC的中点O，OM=1/2AD为定值，所以M的轨迹为以O为圆心圆A半径一半长为半径的圆。

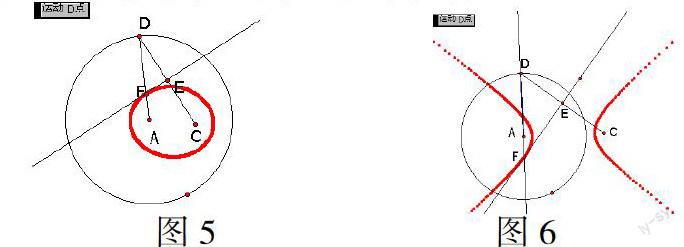
探究2：若C是圆A内一定点，问线段CD的垂直平分线与半径AD的交点F的轨迹图形是什么？

用几何画板进行探究式得点F的轨迹为椭圆（如图5），由学生集体讨论分析为什么？

证明：因为EF为线段CD的中垂线，由中垂线的性质

FD=FC 所以 FA+FC=FA+FD=AD其中AD为定值，点A与点C为定点，且AC

探究3：若拖动点C到圆A外部，问线段CD的垂直平分线与半径AD所在直线的交点F的轨迹图形是什么？

用几何画板进行探究式得点F的轨迹为双曲线（如图6），由学生进一步分析为什么？

证明：因为EF为线段CD的中垂线，由中垂线的性质

FD=FC 所以 其中R为定值，点A与点C为定点，且AC>AD根据双曲线的定义，点F的轨迹是以点A，C焦点，R为实轴长的双曲线.

[总结交流]用“几何画板”的动态功能，探究点的轨迹，通过观察轨迹几何图形，寻找几何不变关系，利用圆、椭圆、双曲线的定义判定轨迹，进而写出轨迹方程。

[拓展探究]

探究4：若C是圆A内一定点，线段CD的垂直平分线与半径AD的交于点F，在直线CF上任取一点L（不是C点）探求点L的轨迹是什么？

用几何画板进行探究得轨迹为椭圆（如图7）.

探究5：若拖动点C到圆A外部，线段CD的垂直平分线与半径AD所在直线的交于点F在直线CF上任取一点L（不是C点）点L的轨迹又会是什么呢？

用几何画板进行探究得轨迹为双曲线（如图8）.

利用几何画板不仅可以让学生在教师的指导下进行探究式学习，还可以让学生主动探究，这样圆中相关的轨迹问题就成为一个开放性问题。

以下学生自主探究内容（让学生猜想探究，用几何画板演示）

自主探究1：在直线EF上取一点S，探求点S的轨迹（如图9）。

自主探究2：在直线CD上取一点T，过T点作CD的垂线TQ交直线AD与Q，探求点Q的轨迹（如图10）。

波利亚说，数学的创造过程与任何其它知识的创造过程一样，在证明一个定理之前，先得猜想，发现出这个定理的内容，在它全面作出详细的证明之前，还得不断检验，完善，修改所提出的猜想，还得推测证明的思路，在这一系列的工作中，需要充分运用的不是论证推理，而是合情推理.利用“几何画板”的动态功能进行探究点的轨迹学习，让学生在动态中观察几何规律，作出猜想，进行合情推理。如在轨迹问题探究1中，改变定点C的位置，线段CD的中点轨迹都是一个圆，学生在观察中找出规律，推理出轨迹圆的半径都为定圆的一半，这样的几何不变关系。

利用“几何画板”进行探究式学习的模式

从实例出发——用“几何画板”进行实验操作——分析验证、发现规律——提出猜想、假设——进行证明——再进一步探究拓展。

【参考文献】

任长松 《探究式学习》 教育科学出版社 2005年2月