不同“视角”，体验别样“精彩”

徐星

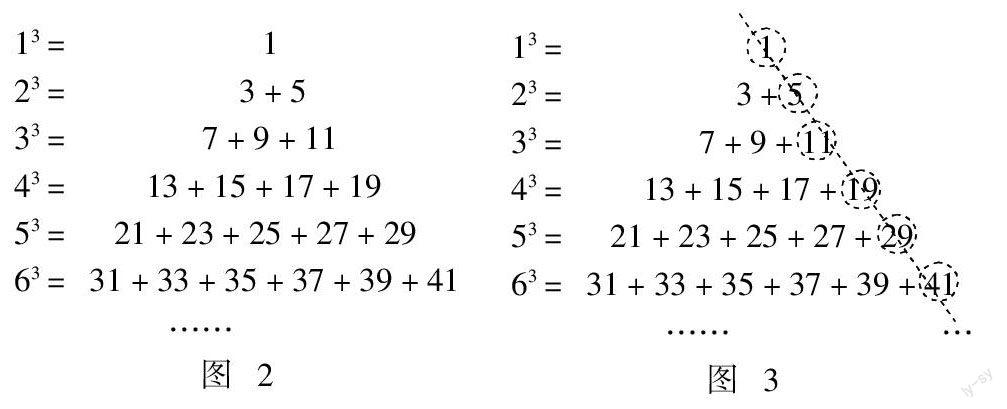
如题：大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和，如23 = 3 + 5，33 = 7 + 9 + 11，43 = 13 + 15 + 17 + 19，若m3分裂后，其中有一个奇数是103，则m的值是 （ ）.

A. 9 B. 10 C. 11 D. 12

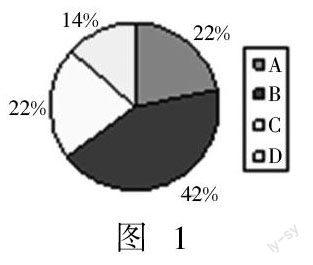
在2014年秋学期七年级期末考试命题中，将这道题作为选择题的最后一题，期望通过这题作为能力题，以便增加考试的区分度.命题之初，预估这道题的难度系数为0.2～0.3，也就是得分率在20%～30%.以班级人均50名同学的学额计算，每班答对人数控制在10～15人. 考试结束后的统计结果如图1.

我所教的班级有51名同学，统计结果表明：其中选择正确的有22人. 也就是该题的得分率比较高，在欣喜之余，我决定找选择正确的22人详细了解这道题的解题思路，以期在解法中遴选优秀的有代表性的思路做有针对性的讲解.

学生甲：根据条件，等式的左边是一个数的立方，等式的右边是连续奇数的和；底数是几，就有几个连续奇数，且下一个立方数的等式的第一个奇数是上一个等式中和最后一个奇数相邻的后一个奇数.于是： 53 = 21 + 23 + 25 + 27 + 29，63 = 31 + 33 + 35 + 37 + 39 + 41，73 = 43 + 45 + 47 + 49 + 51 + 53 + 55，83 = 57 + 59 + 61 + 63 + 65 + 67 + 69 + 71，93 = 73 + 75 + 77 + 79 + 81 + 83 + 85 + 87 + 89，103 = 91 + 93 + 95 + 97 + 99 + 101 + 103 + 105 + 107 + 109.因此103在103对应的等式中，故m = 10.

这时我问：如果不是103，而是1003，那m的值要是确定下来不是就很麻烦啊？学生甲默默地点了点头.我问了一下，用其他方法的人可以自由发表自己的观点.

学生乙：老师，如果将13 = 1补上，那么13 = 1， 23 = 3 + 5， 33 = 7 + 9 + 11，43 = 13 + 15 + 17 + 19，就是从正整数1开始的有规律的一组关于正整数的等式. 等式左边是一个立方数，等式右边是从上往下依次是从1开始的连续奇数的和，且左边底数是几，右边就有几个连续奇数，写成宝塔形就是如图2 .从上往下看最后一个数，如图3：依次是1，5，11，19，29，41，….这些数的规律是m（m + 1） - 1.

当m = 9时，m（m + 1） - 1 = 9 × 10 - 1 = 89；当m = 10时，m（m + 1） - 1 = 10 × 11 - 1 = 109.

103大于89，小于109，故m = 10. 用这个规律很快可以确定1003对应的m = 32.

我追问了一下：你怎么想到将已知条件改写成宝塔形的？学生乙说：以前小学学过的杨辉三角模型就是这个形状，虽然有区别，但是也可以用这个模型来解决这个问题.然后我要求用学生乙的方法的同学也坐下，有其他不同方法的同学自由发表观点.

学生丙：我研究的方法和学生乙差不多，不过我是研究的每个等式的第一个数（如图4），它们依次是：1，3，7，13，21，

31，…. 这些数的规律是m（m + 1） + 1.当m = 10时，m（m - 1） + 1 = 91；当m = 11时，m（m + 1） + 1 = 111. 而103大于91，又小于111，故m = 10.

用这个规律很快也可以确定1003对应的m = 32.

对学生乙、学生丙的解法，我高度肯定了学生丙的建模思想，他们善于从不同的角度，就这些数的特征找到数学规律，利用规律解决问题. 那么，除了从每行最后一列数或者最前一列数这些角度外，能否再从不同角度也能发现规律呢？我不失时机对全班学生进行点拨.

很快，数学课代表提出了他的看法.

学生丁：我研究该模型的中间（如图5），我发现只有当底数是奇数的时候，处在最中间的一列数分别为1，9，25，49，…. 这些数正好是底数的平方. 如果m = 9，那么最中间的数是81，于是81后面连续四个奇数分别为83，85，87，89；如果m = 11，那么最中间的数是121，和121相邻的前面五个奇数分别为119，117，115，113，111；103只能在第10行，故m = 10.

学生丁的视角指向奇数行，并且从奇数个数中找“中位数”这一特定的数发现规律，并从规律中找到解决问题的途径，但是要想顺利地找到1003对应的m值，还是具有一定的难度，因为找到了“中位数”以后，还必须写出当m = 31时和它相邻的后15个奇数以及m = 33时和它相邻的前16个奇数方可确定m = 32.

学生丁的发言刚刚结束，班长迫不及待想要表达自己的观点：

在图5中，在偶数行分别插入一列数：4，16，36，…，插入的这些数正好是底数的平方，因为它们是偶数，所以它们不可能分布在每一行中，因此，以该平方数为中心，成对写出相邻的奇数，使得它们的平均数就是该平方数. 因此在该模型中可以发现：奇数行和偶数行都可以看成最中间的数一定是一个完全平方数，而且和等式前面的立方数底数相同. 当m = 9时，最中间的数是92 = 81；当m = 10时，最中间的数是102 = 100是插入的数，成对就可以得出该行的十个数分别为99，101；97，103；95，105，；93，107；91，109. 显然m = 10. 而且当m = 32时，最中间的数是322=1024是插入的数，以1024为中心成对写出16对奇数，其中有一对是1003，1045，所以1003在第32行.

结合学生丁和班长的发言，我进行了及时的归纳：就每一行的特征看，如果m是奇数，m3 = [m2 - （m - 1）] + … + （m2 - 2） + m2 + （m2 + 2） + … + [m2 + （m - 1）]；如果m是偶数，m3 = [m2 - （m - 1）] + … + （m2 - 1）+（m2 + 1） + … + [m2 + （m - 1）].

“横看成岭侧成峰，远近高低各不同”，诗人描写的意境启迪我们，要努力培养学生从不同的角度思考数学问题，对于学生甲的数学思考，不能说不好，至少他的方法使他体验到成功后的喜悦；学生乙、丙、丁的数学思考，从不同的观察角度，发现并找到规律并利用规律解决问题，尤其是学生乙，能将学到的杨辉三角模型用来解决问题，知识的储备在解决这一题的时候为同学们解决问题提供一个很好的数学模型，将一连串看似简单，实则复杂的数学问题模型化. 班长的思路最值得提倡，为了找出规律，从中间线上的数据入手，发现规律，并利用规律完美地解决问题.

因此，数学老师要鼓励学生从不同的角度进行数学思考，在不同角度进行数学思考的过程中，一步步发现数学问题的本质，揭开数学问题的“庐山真面目”.只有这样，学生对数学问题的探索兴趣会越来越浓，学生对数学问题的解决欲望会越来越强，培养学生真正的数学思考的能力.