数学教学应重视知识的形成过程

宜延安

【摘要】在教学中，只有重视数学知识的形成和发展过程，解题思路的分析和探索过程，解题方法及规律的概括和总结过程，才能使学生在这个过程中展开思维，掌握“双基”提高能力，从而真正起到事半功倍的效果。

【关键词】形成 推导 思考 运用

中学数学课程标准明确指出：“数学教学不仅要教给学生数学知识，而且还要揭示获取知识的思维过程。”这就要求我们，在平时的数学教学中不能仅仅告诉学生具体的数学知识是什么，而更应该重视知识形成过程的教学。现在我想从以下四个方面谈一谈我的看法。

一、数学教学应重视概念形成过程的教学

数学知识都是以概念为基础的，要使学生获得系统的数学知识，首先必须获得清晰明确的数学概念。数学概念是现实世界事物（数量关系和空间形式）的本质属性在人们头脑中的反映。在教学中，对于一些概念、定义的教学，如果我们只注重“结果”，直接把定义教给学生，然后让他们在一知半解的基础上死记硬背，那么他们总是难于理解和掌握。如果我们通过举例子、打比方、作比较、记口诀等一系列教学方法重视概念的形成过程教学，学生理解和掌握起来就容易多了。而中学数学教学中的数学概念是指教材中的那些数学名词、术语等所反映的概念，其中绝大多数概念是以定义的形式表示出来。定义的重要使命是总结研究的结果，把获得结果凝结在一个简练的形式（语句）中，从而揭示出区别于其它事物的本质属性。

例如，初中数学中圆的定义，它是一个比较抽象的定义，学生不容易理解。在教学中，可先向学生渗透集合的观点，再引导学生指出确定一个圆需要的两个因素（一是位置，二是大小）归纳，抽象出圆的定义。这样，学生对圆的概念就理解得深，掌握得牢。再比如完全平方公式，虽然这个公式比较容易理解，但往往有些学生很容易将完全平方公式中的“和”“差”记混淆。因此，我们在教学中可采取先讲解公式推导，再总结口诀得方式“首平方，末平方，首末两倍中间放，符号与前一个样。”这样学生在理解的基础上进行记忆，不仅可以记得牢，而且在以后的应用中也不容易出错，何乐而不为呢？

二、定理、法则的推导过程远比定理法则更重要

对于定理、公式和法则的教学，我们不仅仅是让学生知道了这个定理、公式法则或是让学生记住了这个定理、公式法则，而是更应该重视其发现，推导证明的思维过程，使学生完全了解这些知识是如何发现的，如何获得的，这样他们在以后的应用中才能得心应手。

例如，对于多边形内角和定理的教学，是在学习了三角形内角和定理及多边形对角线的基础上进行的。将一个多边形从同一顶点引所有的对角线，这样就将多边形分成了许多个三角形，再让学生思考如何证明多边形的内角和定理。这样，学生不仅复习巩固了三角形内角和定理，也学习了如何将多边形转化为三角形，还从中掌握了分类、转化、归纳以及从特殊到一般等多种数学思想方法。

三、重视问题的思考探索过程

无论是证明题（包括证明定理）、计算题还是作图题，重要的是教给学生分析、归纳、综合、猜想、探索解题思路和方法，这样才能不断提高学生分析问题和解决问题的能力。

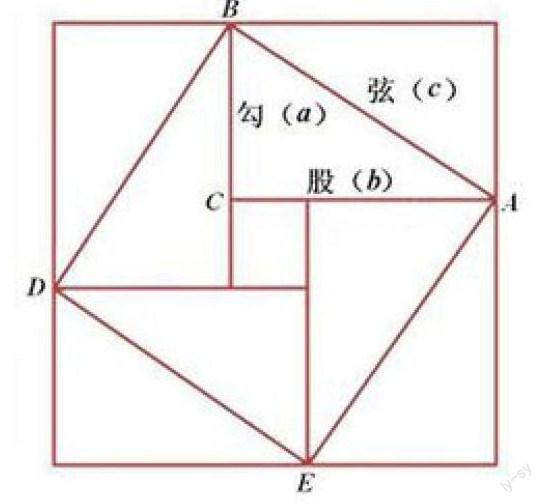
例如，勾股定理的证明过程就非常具有代表性。我国汉代的赵爽在注解《周髀算经》时给出的证法就堪称完美，人们称它为“赵爽弦图”。赵爽根据此图指出：4个全等的直角三角形可以围成一个如图所示的大正方形，而中空的部分是个小正方形。也就是说大正方形的面积等于4个小三角形的面积加上中间一个小正方形的面积，这样就将勾股定理的证明推向了艺术的高度。

四、数学教学应重视知识的反复运用，并及时巩固

学习知识的目的在于运用，一个新知识体系建立之后，要通过解题反复运用不断实践，从各个方面，使新知识体系不断巩固和强化。要把新知识体系作为判断的工具来使用，通过训练，使学生将所学的新知识转化为学生自身的技能技巧，转化为学生的心理品质。在解题训练过程中，要善于运用有关知识组成恰当的判断，进行逻辑推理，不断地加深对所学知识的理解和掌握。数学知识的形成过程是数学知识的重要环节，教学时，要从需要出发、从实际出发，从学生所熟悉的事物出发，从易到难，由浅入深，循序渐进。

数学教育家曹才翰先生说得好：“数学学习与其说是学习数学知识，倒不如说是学习数学的思维过程。”在教学中，只有重视数学知识的形成和发展过程，解题思路的分析和探索过程，解题方法及规律的概括和总结过程，才能使学生在这个过程中展开思维，掌握“双基”提高能力，从而真正起到事半功倍的效果。