基于思维导图下的数学问题解决

袁慧

【摘要】思维导图是一种可视化的图表，能够充分调动大脑进行思维发散.在数学问题解决过程中，思维导图能够将错综复杂的数学知识以及想法连接起来，并有效地加以分析，从而最大限度地实现问题解决.

【关键词】思维导图；问题解决；数学

思维导图（MindMapping），也称为心智图.20世纪70年代被称为“世界记忆之父”的托尼.巴赞发明的“一种非常有用的图形技术”.思维导图由主题、节点、连线、图像和色彩构成，由中心主题分支出节点，节点分支出子节点，并由此发散，随着思维的不断深入，节点不断增加，逐步形成一个向周围发散而有序的树状图.通过捕捉和表达发散，思维导图能够将大脑内部零乱、枯燥的信息用一种有序的、条理清晰的可视化图表呈现出来，从而充分开发大脑潜能，极大激发人们的创造能力.

在数学教学中经常会出现这样一种现象：有些学生上课很认真听讲，听也听懂了，但到做作业时却束手无策；有些学生能够解决熟悉的问題，遇到新问题却无从下手.究其原因，这些学生并没有真正理解.爱因斯坦曾说过：“结论几乎总以完成的形式出现，读者体会不到探索和发现的喜悦，感觉不到思想形成的生动过程，也就很难达到清楚、全面理解的境界.”在问题解决过程中，教师运用思维导图将自己的探索过程、试误过程以及思考的方向等呈现给学生，让学生掌握解决问题的思路是至关重要的.在构作思维导图的过程中，也是师生之间进行交流互动的过程，促使学生的学由“被动”向“主动”转化，让学生积极主动参与到整个教学过程中，提高教学效率.正如英国教育学家哈曼所说：“那些不设法勾起学生求知欲望的教学正如捶打着一块冰冷的生铁.”把解题的思想方法和过程呈现给学生，激发他们自主体会，积极探索，从而到达真正理解.

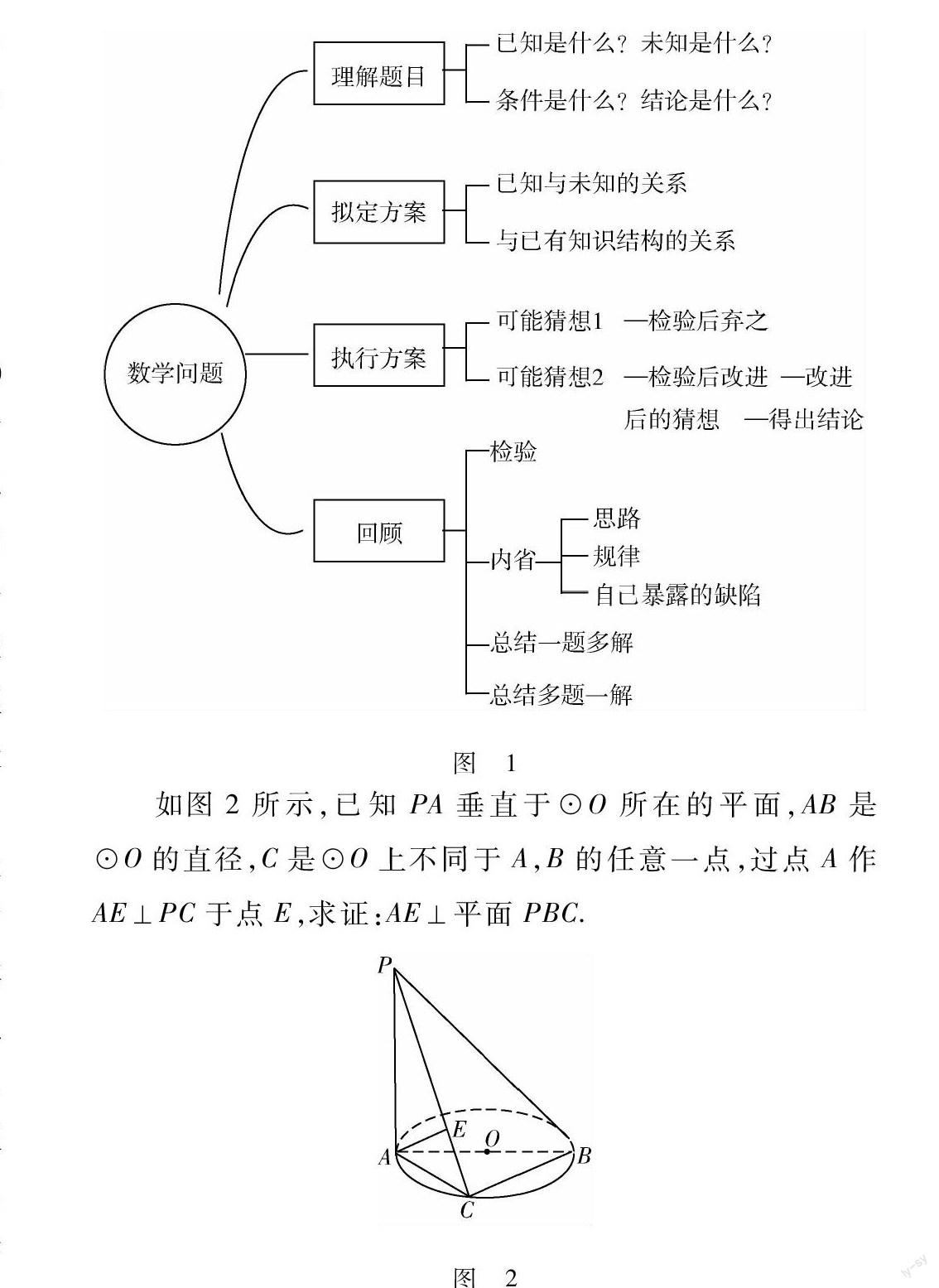
毫无疑问，在数学问题解决研究中的标志性人物当属波利亚.波利亚将解题过程分为四个阶段：理解题目，拟定方案，执行方案，回顾，每一阶段都注重引导学习者进行思维发散.笔者结合自己对波利亚的“怎样解题表”的理解，绘制如下解题思维导图（如图1）.

图1

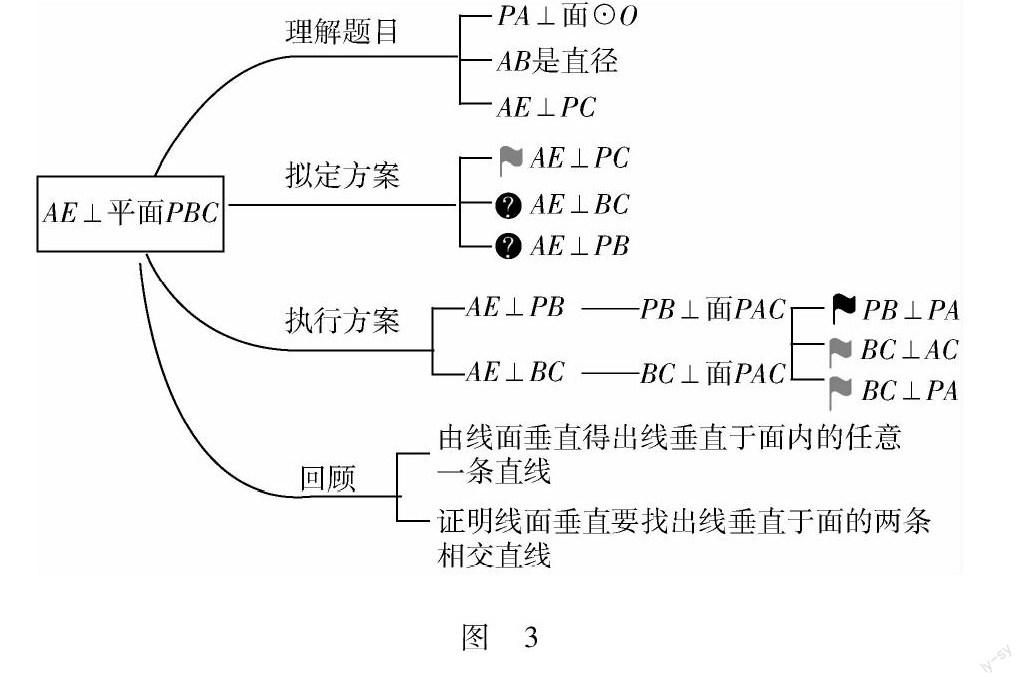
如图2所示，已知PA垂直于⊙O所在的平面，AB是⊙O的直径，C是⊙O上不同于A，B的任意一点，过点A作AE⊥PC于点E，求证：AE⊥平面PBC.

图2

这道题的分析过程：结论是要证AE⊥平面PBC，要证明线面垂直就要找出线垂直于面内的两条相交直线，题上已知AE⊥PC，只需再证AE⊥BC或者AE⊥PB，不管选择哪个垂直来证明，都需要证明两条异面直线垂直，都要由线面垂直来证得.至于选择证BC⊥平面PAC还是选择证PB⊥平面PAC比较好，我们要再回到已知条件，根据PA垂直于⊙O所在的平面，AB是⊙O的直径，可以得出AC⊥BC，PA⊥BC，也即证得BC⊥平面PAC，那么AE⊥BC即得证.上述思维过程，如果只用文字来表述就会显得冗长，不易解读，但如果结合如下思维导图（如图3）进行讲解，思维过程就会清晰明了的多.实践证明：思维导图为学生提供了解题框架，在数学问题解决中引入思维导图，能够有效加强信息之间的全面性和关联性，从不同角度，不同层次引导学生所能想到的知识点和解题思想方法，师生共同探索出一个或

多个解题方案，让学生在整个解题过程中真正了解在什么情况使用什么方法，采取哪种方案更有利于问题解决.“我图画我心”，教师通过学生画出的思维导图，能够知道学生的认知结构，可以很容易了解到学生对问题的理解程度、解题思路以及在问题中暴漏出的不足与错误，找出学生解题过程中的易错点与闪光点，对不同的学生进行有针对性的指导，因材施教.通过将自己的思维导图与教师制作的思维导图作对比，学生能够及时地查漏补缺，最大限度地提高学习效率.

图3

备注：绿色红旗表示“Yes”，黑色表示“No”，问号表示“Question”.

基于思维导图的数学问题解决以核心问题为主线，并将主要问题分解为若干小问题，以问题引导学生思考，将知识的学习贯穿在问题的思考之中.国外的研究发现，学生拥有组织性的知识可以建立学习的“脚手架”，更易产生有意义的学习，思维导图以一种非线性组织形式，整合结构图与文字表征，比传统的文字性叙述更能清晰表征知识，从而促进有效学习的发生和新旧知识之间的整合与建构.基于思维导图下的问题解决可以沟通各部分内容之间的联系，感受数学的整体性，充分调动学生的积极性，激发学生的创新潜能.