“知识发明”教学法示例：欧拉角教学设计

穆华　吴美平　潘献飞

[摘 要]大学课堂教学的一种成功方式是引导学生自己将所要讲授的知识重新“发明”出来。大学老师提出一个或多个问题作为引子，然后引导学生利用已有知识解决所提出的引子问题，并在解决问题的过程中推导出新知识。这种“知识发明”的教学方式有利于调动学生的主观能动性，营造良好的课堂氛围，提高学生解决问题的能力，帮助学生构建系统的知识结构。

[关键词]欧拉角 教学设计 知识发明

[中图分类号] G642 [文献标识码] A [文章编号] 2095-3437（2015）03-0163-03

所谓“知识发明”教学法，是指老师在课堂教学中设计合理的问题，引导学生利用已有的知识解决问题，并在解决问题的过程中“发明”出新知识的一种教学方式。全国数学名师李尚志在教学中推行这种教学方式，他在自己编著的教材《线性代数》[1]中写到：“不从定义出发而从问题出发引入概念，引导学生在尝试解决这些问题的过程中将所要讲授的知识重新‘发明出来”。我们在教学实践中积极采用“知识发明”教学法，尝试通过引导学生解决问题来组织课堂教学，收到了良好的教学效果。本文以本科导航类专业课程中欧拉角的教学设计为例，来说明这种教学方式。描述空间直角坐标系（下文简称“坐标系”）空间关系的欧拉角在理论力学[2]、飞行力学[3] [4]和导航专业课程[5] [6]中都有所涉及。学生在不同课程中多次学习相关内容后，往往还存在以下问题：不能快速找出两个坐标系之间的欧拉角，对12种欧拉角的存在性心存疑惑等等。究其原因，从教材编写到老师授课，往往把重点放在结论上，直接把结论灌输给学生。如果按照教材编写授课，欧拉角的引入通常是一句话“欧拉首先提出可以用三个角度来描述刚体的转动”。接下来就是“拿来主义”，将欧拉提出的欧拉角拿来用。但是学生对于这种拿来的东西往往只知其一、不知其二，很难真正拥为己有。我们在教学实践中尝试引导学生自己把欧拉角“发明”出来，这种课堂教学有助于调动学生的学习兴趣，使学生自主更新知识体系，从而优化教学效果。

一、欧拉角的引入

两个平面直角坐标系的空间关系用一个转角就可以刻画，这是学生所熟悉的，由此引申到空间直角坐标系，请学生思考：能否用转角来刻画两个空间直角坐标系的空间关系？

（一）引子问题

设O-xpypzp和O-xqyqzq是两个原点重合、坐标轴方向不重合的空间直角坐标系，分别以P和Q表示。确定两个坐标系的空间关系可以通过确定坐标系Q在坐标系P中的位置来实现，这相当于取坐标系P为参考坐标系。那么如何确定坐标系Q在坐标系P中的位置呢？

（二）解答

两个平面直角坐标系的空间关系用一个转角就可以刻画。能否用转角来刻画两个空间直角坐标系的空间关系呢？

确定坐标系Q在坐标系P中的位置，只需依次确定坐标系Q的两个坐标轴的位置，以依次确定Oxq轴和Oyq轴的位置为例。

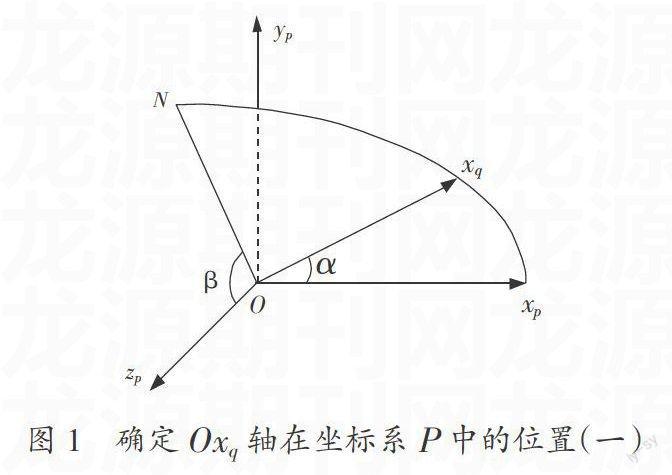
首先确定Oxq轴。在图1中，ON是Oxq轴与OxP轴所在平面OxqxP与平面OypzP的交线，同时是Oxq轴在平面OypzP内的投影。ON到OzP轴的转角记为β，OxP轴到Oxq轴的转角记为α。两个转角可以唯一确定Oxq轴在坐标系P中的位置。对于转角，规定逆时针转动为正，转角取值范围限制为（-180°，180°）。

Oxq轴的位置确定后，由于Oyq轴被限定在Oxq轴的垂面内，所以只需要一个角度来确定Oyq轴在垂面内的位置便可以确定Oyq的空间位置。Oxq轴和Oyq轴的位置确定后，Ozq轴的位置由右手法则确定。可见，可以利用三个转角确定一个坐标系相对于另外一个坐标系的空间关系。

（三）点评

利用两个转角刻画Oxq轴在坐标系P中的位置，这种方式也提供了通过两次转动使得OxP轴与Oxq轴重合的方案。

（1）首先，坐标系P绕OxP轴转动角度90°-β，使得OyP轴与ON重合，得到的中间坐标系记作Ox′P y′P z′P；

（2）接下来，中间坐标系Ox′P y′P z′P 绕OzP 轴转动角度α，便可以使得Ox′P 轴与Oxq轴重合，得到的中间坐标系记作Ox″P y″P z″P。

当坐标系P经过两次转动使得OxP轴与Oxq轴重合后，中间坐标系Ox″P y″P z″P的Oy″P轴与Oyq轴同位于Oxq轴的垂面内，Oyq的空间位置可以用Oy″P轴到Oyq轴的转角γ来刻画。同时，只需将中间坐标系Ox″P y″P z″P再绕重合的坐标轴Oxq轴转动角度γ，便可以使得坐标系P与坐标系Q重合。可见，三个转角<90°-β，α，γ>及转动顺序（1、3、1）（这里1、2、3分别表示坐标系的x轴、y轴、z轴）可以完整刻画两个坐标系的空间关系。这里的转角就称作欧拉角。至此，我们顺理成章的引入了欧拉角的概念。

二、欧拉角的分析

（一）欧拉角的组数

显然，用欧拉角确定两个原点重合坐标系的空间关系有多种选择。一方面，通过两次转动重合的坐标轴可以在第一轴、第二轴和第三轴之间任意选择；另一方面，通过两次转动使一组坐标轴重合也有多种实现方式。下面以Oxq轴与Oxp轴重合为例，分析所有实现方式。

（1）利用Oxq轴与Oxp轴所在平面Oxqxp（见图1）。在对引子问题解答的点评中，给出了按照1、3顺序转动的方案<90°-β，α>。也可以采用另一种方案使得Oxp轴与Oxq轴重合。首先坐标系P绕Oxp轴转动，使得Ozp轴与ON重合，然后绕中间坐标系的Oy′P 转动使Ox′P 轴与Oxq轴重合。两次转动的角度分别为-β和-α，转动顺序为1、2。

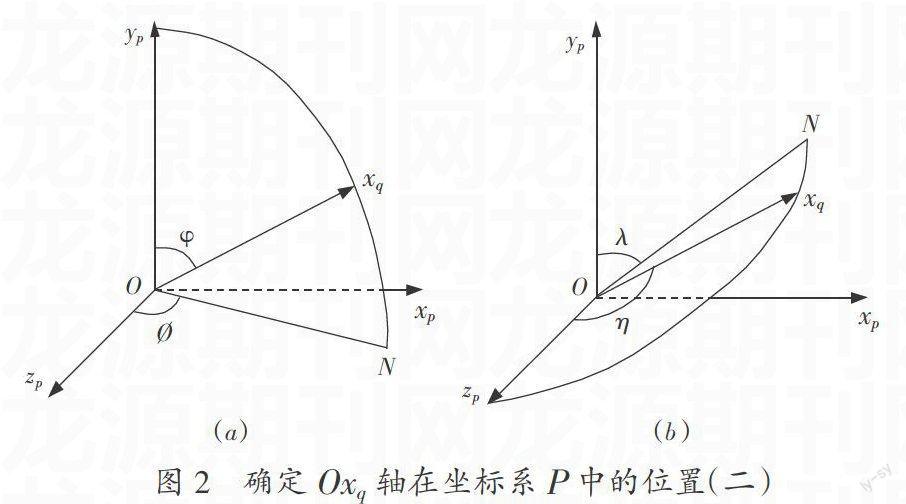
（2）利用Oxq轴与Oyp轴所在平面Oxqxp（见图2a）。只有一种方案：先绕2轴转动使得Oxp轴与ON（Oxq轴在平面Oxpzp的投影）重合，然后绕3轴转动到达Oxq轴的位置。两次转动的角度分别为？覫-90°和90°-φ，转动顺序为2、3。

（3）利用Oxq轴与Ozp轴所在平面Oxqzp（见图2b）。只有一种方案：先绕3轴转动使得Oxp轴与ON（Oxq轴在平面Oxpyp的投影）重合，然后绕2轴转动到达Oxq轴的位置。两次转动的角度分别为90°-λ和η-90°，转动顺序为3、2。

可见，通过两次转动使一组坐标轴重合有四种转法，相应的首先使该组坐标轴重合，然后再使两个坐标系重合的转法也就有四种，对应四组欧拉角。转动使两个坐标系重合时首先重合的轴有三种选择，因此使两个坐标系重合的转法有12种，对应12组欧拉角。

（二）特殊情况

本文所考虑的两个坐标系的坐标轴方向不重合。当两个坐标系的1轴共坐标系P的坐标平面，即Oxq轴位于平面Oxpyp或者平面Oxpzp内时，上述四种转动方案退化为两种。以Oxq轴位于平面Oxpyp内为例，设Oxp轴到Oxq轴的转角为θ，一种方案为按照1、2顺序转动<-90°，-θ>，另一种方案为绕3轴转动θ。此时，如果两个坐标系的2轴和3轴均不共坐标系P的坐标平面，那么使两个坐标系重合的欧拉角有10组，其中一组仅有两个欧拉角。如果两个坐标系的另外一组坐标轴也共坐标平面，例如Oxq轴位于平面Oxpyp内，同时Oyq轴位于平面Oypzp内时，使两个坐标系重合的欧拉角有8组，其中两组仅有两个欧拉角。

（三）确定坐标系转换的欧拉角

在可以实现两个坐标系转换的多组欧拉角中，有些欧拉角可以由已知条件直接获得。清楚欧拉角的来源，可以帮助学生快速确定合适的欧拉角及转动顺序。考虑下面的例子。

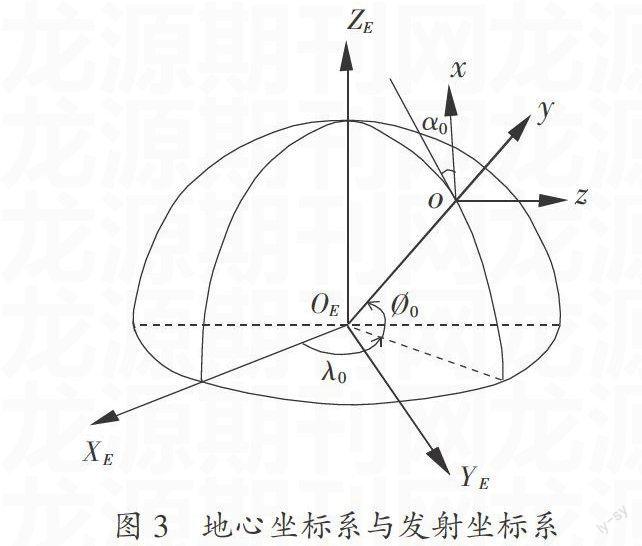
设地球为一圆球，地心坐标系的原点在地心OE，OEXE轴在赤道平面内指向发射时刻的起始子午线并随地球一起转动，OEZE轴垂直于赤道平面指向北极。发射坐标系的原点与发射点o固连，发射点的经度为λ0、地心纬度为？覫0；ox轴在发射点水平面内，与o点正北方向的夹角为α0；oy轴垂直于发射点水平面指向上方。如图3所示。

从欧拉角的引入过程不难体会到，确定欧拉角关键是要找到两个坐标系的某两个轴所在的平面，并且能够确定这个平面在参考坐标系中的位置及平面内两个坐标轴的相对位置。在图3中，发射点o所在子午面正是这样一个平面，它是oy轴和OEZE轴所在平面，其位置可以用发射点的经度λ0来刻画，子午面内oy轴的位置可以用发射点的地心纬度？覫0描述。由此可以确定使地心坐标系与发射坐标系各对应轴平行的三个欧拉角，λ0-90°、？覫0、-（-90°+α0），转动顺序为3、1、2。

说明：这部分属于后续教学内容，不属于本次课内容。这里是为了表明学生自己“发明”欧拉角后，在确定坐标系转换的欧拉角时可以更加得心应手，因此老师在后续课堂教学中可以少用课时。

三、结束语

对于通过解决问题引入新知识的教学方式，我们有以下体会：

1）设计的问题要容易解决，这样才能调动学生的积极性。在本次教学设计中，引子问题的求解仅用到了中学几何知识，能够调动学生的积极性和信心。

2）与传统教学相比，这种教学方式可能需要多一些教学时间；但是由于学生对新知识的理解更为深刻，所以后续教学往往可以少用课时，总的教学时间是相当的，而教学效果会更好。在本次课中，让学生自己“发明”欧拉角的方式比“欧拉提出了欧拉角”一句话引入方式用的课时要多一些，但在后续教学“常用坐标系及其相互转换”中学生可以很快的确定常用坐标系之间的欧拉角，与传统教学方式相比可以少用课时。

[ 参 考 文 献 ]

[1] 李尚志.线性代数[M].北京：高等教育出版社，2011.

[2] 孙世贤.理论力学教程[M].长沙：国防科技大学出版社，2009.

[3] 钱杏芳，林瑞雄，赵亚男.导弹飞行力学[M].北京：北京理工大学出版社，2011.

[4] 胡小平，吴美平，王海丽.导弹飞行力学基础[M].长沙：国防科技大学出版社，2006.

[5] Titterton D.H.and Weston J.L.，Strapdown Inertial Navigation Technology[M]，2nd Ed，The Institution of Electrical Engineers，2004.

[6] Grewal M.S.，Weill L.R. and Andrews A.P.，Global Positioning Systems，Inertial Navigation and Integration [M]，New York：Wiley，2001.

[责任编辑：林志恒]