夯实基础 逐步推进教学过程

李朝阳

摘   要：二次函数是初中数学学习中的重点和难点，结合教学实践，就初中数学中二次函数的教学方法和思路从画图、看图、求解析式、关键点特征、应用等几个方面的逐步推进进行了分析和探讨.

关键词：二次函数;画图;看图;关键点;应用

二次函数是初中九年级的教学内容，是初中函数中最难掌握的一章，在初中数学中占有重要的地位，作为初高中衔接的内容，在中考中也占有较大的份量，学好二次函数，对数学知识的理解和应用有重要意义，下面对如何循序渐进、条理清楚的学好二次函数做探讨.

1   学会画图

1.1   画y=ax2（a≠0）的图像

用列表、描点、连线法画出二次函数的图像，让学生体会到二次函数的图像是抛物线，a决定抛物线的开口方向和开口大小.

1.2   画y=a（x-h）2+k（a≠0）的图像

让学生体会到抛物线的顶点为（h，k），而抛物线的开口方向和开口大小仍是由a决定.而y=ax2可看作y=a（x-0）2+0，顶点坐标为（0，0）.

1.3   画y=ax2+bx+c（a≠0）的图像

先配方成y=ax+2+，从而h=-，k=，函数解析式简写为：y=a（x-h）2+k，顶点坐标为（h，k），即（-，）.

综上所述，系数a决定了抛物线的开口方向和开口大小，系数b、c与a决定抛物线的位置;对于抛物线的上下左右移动，由于平移前后两图形是全等形，所以平移前后a不变，只是顶点（h，k）位置发生变化，而对于平移的规律，要紧紧抓住抛物线的顶点位置的变化来定顶点坐标.如：把二次函数y=2x2-4x-1=2（x-1）2-3的图像向左平移2个单位、向上平移1个单位，只要关注抛物线原顶点（1，-3），平移后顶点（-1，-2），而平移前后a不变，则平移后解析式为（尽可能用顶点式）：y=2（x+1）2-2.

2   学会看图

2.1   看函数图像与系数a的关系

a>0开口向上，a<0开口向下，|a|越大，开口越小;|a|越小，开口越大.

2.2   看函数图像与系数b的关系

由对称轴方程x=-可知，若抛物线的对称轴在y轴左侧，则对称轴x=-<0，则>0，a、b同号;抛物线对称轴若在y轴右侧，则对称轴x=->0，则<0，a、b异号.

2.3   看函数图像与系数c的关系

抛物线与y轴的交点的纵坐标即为c.

2.4   看函数图像与h、k的关系

抛物线的顶点位置为（h，k），h=-，k=.

2.5   看增减性

图像从左向右看，若在某个区域（对称轴的同一侧）是连续的上坡，则是y随x的增大而增大，反之若在某个区域（对称轴的同一侧）是连续的下坡，则是y随x增大而减小.

2.6   看某些自变量取特殊值时的函数值

如当x=1时，可看出a+b+c的值;当x=-1时，可看出a-b+c的值;由图像也可直接看出函数图象的最高点（最大值）或最低点（最小值）.

2.7   看二次函数所对应的方程的解与不等式的解集

抛物线与x轴的两个交点的横坐标即为对应的一元二次方程的解，交点的个数也是函数对应的一元二次方程解的个数;而不等式的解集可由函数图像直接看出：图像在x轴上方对应的x的解集即为不等式ax2+bx+c>0的解集，在x轴下方对应的的解集即为不等式ax2+bx+c<0的解集.

例1   （图1）若二次函数y=ax2+bx+c（a≠0）再加一些条件，则可以看出图像与a、b、c取值的更多的结论.如二次函数y=ax2+bx+c过（-1，2）与（1，0）且与y轴交于负半轴，则我们可以看出如下的结论：

1. a>0;

2. 对称轴在y轴右侧，a、b异号，b<0;

3. c<0;

4. 顶点在第四象限h>0，k<0;对称轴x=-<1，可得2a+b>0;

5. 在对称轴的左侧，y随x增大而减小，在对称轴的右侧，则是y随x增大而增大;

6. 图像过（-1，2）、（1，0），∴a-b+c=2a+b+c=0，

解得b=-1a+c=1;又∵c<0，∴a>1.

3   学会求二次函数解析式

3.1   一般式：y=ax2+bx+c（a≠0）

已知三个点（一般是普通点），用一般式求解.

3.2   交点式：y=a（x-x1）（x-x2）（a≠0，△≥0 ）

已知三个点（与x轴的两个交点和另一个点），可选用交点式求解.

3.3   顶点式y=a（x-h）2+k（a≠0）

已知两个点（一个顶点和另一个任意点），可选用顶点式求解.

当然，交点式的条件也适用于一般式，只是计算方面的简易问题。有时也不一定是上述的这三种情况，但多是这三种情况的延伸，如已知对称轴和两个已知点，就相当于告知对称轴方程x=h=-;已知最值，就相当于告知方程y=k=-，再结合其它的条件求解，而已知顶点的坐标相当于已知两个普通点的坐标.

4   学会求特殊点构成的图形面积、特殊点构成的图形特征、对称轴

关键点A、B、C、D（抛物线与x轴两交点为A、B，抛物线与y轴的交点为C，抛物线顶点为D）所构成的△ABC、△ABD的面积求解;当△ABC、△ABD为Rt△时a、b、c的特征;对称轴的另外求解方法.

例2  （图2）： 以a>0，△>0即抛物线开口朝上、四个点都存在为例进行研究.已知抛物线与x轴两交点为A（x1，0），B（x2，0），与y轴交于C（0，c），顶点D（-，）.

4.1   △ABC、△ABD的面积与a、b、c的关系

|AB|=|x1-x2|=-

==.

S△ABC=|AB|·|OC|=··c=·.

S△ABD=|AB|·|DE|=··

==.

4.2   若△ABD是直角三角形

抛物线是轴对称性图形，A、B是对称点，易知△ABD是等腰三角形，E为线段AB的中点;则Rt△ABD中，AB=2DE ，即=2·=，

解得，Δ=4.

4.3   若△ABC是直角三角形

则A、B两点必定在y轴的异侧，∴x1、x2必定异号.∵OC⊥AB于O点，∴Rt△ABC中，OC2=OA·OB，即c2=x1·x2， ∴c2=-，解得ac=-1.

4.4   对称轴

x=-=-==

==-;当交点坐标不是A（x1，0）、B（x2，0），而是E（x1，h）、F（x2，h），h≠0、 时，上面求对称轴的公式x=一样可用，因为一元二次方程ax2+bx+（c-h）=0在求对称轴时用x=-只与a、b有关，而与常数c-h无关.

5   学会二次函数的实际应用

5.1   应用于解决实际问题中的面积最值问题、利润最大问题

面积最值问题与利润最大问题都是先由题目条件，构造出二次函数关系，然后配方求顶点坐标，从而得出面积、利润的最大（小）值;但是当顶点横坐标不在自变量的取值范围内时，则顶点不可用，最大（小）值就不是顶点纵坐标，而应在自变量的取值范围内来寻找相应的最大（小）值.

例3   （图3）：用一段长为30 m的铁丝网围成一个一边靠围墙的矩形场地，墙长为10 m，这个矩形的长、宽分别是多少米时，矩形场地的面积最大？最大面积是多少？

设BC=x（0

当x=15时，S最大为，但x=15时已超过墙长10 m.

∴x=15不在自变量的取值范围内，不可用，这时在自变量取值范围0

5.2   应用于解决实际问题中的石拱桥问题

这类问题的重点是建立合适的平面直角坐标系，并且把相关数据转化到图形坐标中，然后利用二次函数知识解决问题.

例4   图4是一个抛物线形拱桥，当水面在l时，拱顶离水面2 m，水面宽4 m.若货船在水面上的部分的横截面是矩形，已知货船的宽为2.9 m，且船高出水面1 m，问货船能否顺利通过这座桥？[答案：不能]

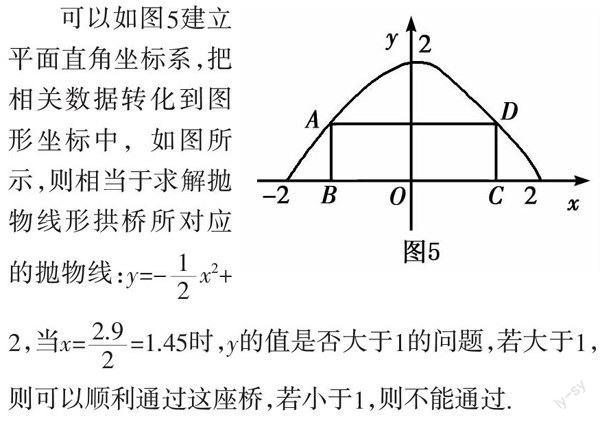
可以如图5建立平面直角坐标系，把相关数据转化到图形坐标中，如图所示，则相当于求解抛物线形拱桥所对应的抛物线：y=-x2+2，当x==1.45时，y的值是否大于1的问题，若大于1，则可以顺利通过这座桥，若小于1，则不能通过.

6   利用二次函数的性质解决其他实际问题

二次函数还可以解决诸如刹车距离与时间问题、投篮等体育运动问题等，这类问题一般难度不大，而应用于与其它图形（直线、三角形、四边形、圆等）的结合则题型较多，一般作为二次函数压轴题考查，如下面两种类型：

6.1   图形运动问题

要注意用运动与变化的眼光去观察和研究图形，把握图形运动与变化的全过程，抓住其中的等量关系和变量关系，并特别关注一些不变的量、不变的关系或特殊关系，善于化动为静，由特殊情形（特殊点，特殊值，特殊位置，特殊图形等）逐步过渡到一般情形，综合运用各种相关知识及数形结合、分类讨论、转化等数学思想加以解决.当一个问题是确定有关图形的变量之间的关系时，通常建立函数模型或不等式模型求解;当确定图形之间的特殊位置关系或者一些特殊的值时，通常建立方程模型去求解.

6.2   存在性问题

当二次函数与三角形、四边形和圆综合考查时，需要用到数形结合思想解决这类问题，把“数”与“形”结合起来，互相渗透;而存在探索型问题是指在给定条件下，判断某种数学现象是否存在、某个结论是否出现的问题.解决这类问题的一般思路是先假设结论的某一方面存在，然后在这个假设下进行演绎推理，若推出矛盾，即可否定假设;若推出合理结论，则可肯定假设.

在二次函数的教学中要充分体现数形结合的数学思想，本章知识对学生基本数学思想和素养的形成起重要推动作用.所以我们应从培养学生的观察能力入手，运用数形结合的思想，通过对比、分析、归纳的方法进行二次函数的教学，激发学生的学习兴趣， 并加深对二次函数的理解和掌握.同时，又能使学生学到学习和探究问题的方法，为今后的学习奠定良好的基础，从而提高学生分析问题和解决问题的能力.