优化定理教学 发展学生思维

王春华

摘   要：在定理教学中，创设适当情境，让学生发现问题，提出问题进行研究，历经猜想、探究、失败、反思、再探究、发现，类似于科学家进行科学研究的过程，可极大地调动学生学习的主动性和创造性，从而达到发展学生思维能力的目的.

关键词：定理教学;思辨能力;推理能力;创新意识

数学定理不仅表达了重要的数学事实，是定义的延伸，而且集中地反映了数学思想、数学方法，反映了前人探究和创新的成果，是提高学生综合素质的好素材.在定理教学中，创设适当情境，让学生发现问题，提出问题进行研究，历经猜想、探究、失败、反思、再探究、发现，类似于科学家进行科学研究的过程，可极大地调动学生的主动性和创造性，从而达到发展学生思维能力的目的.

结合自己多年的教学实践，本文就“初中数学课堂中，如何优化定理教学，发展学生的思维能力”，谈一谈自己的几点体会，与同行们商榷.

1   立足定理讨论，发展学生的思辨能力和求真精神

思辨能力就是思考辨析能力，是一种抽象思维能力.求真即追求真理，是指在科学理论与方法的指导下不断地认识事物的本质，把握事物的规律. [1 ]

很多数学定理都带有高度的抽象性和概括性，不容易理解，给学生造成很大的困惑，致使课堂气氛显得沉闷，学习积极性不高，容易形成教师的一言堂.而这种课堂教学往往过多地发挥教师的主导作用，限制了学生思辨能力的发展.久而久之，学生对数学定理的学习不再有好奇心，也就无从谈及培养学生的思辨能力了.因此教师应以发展学生思辨能力和求真精神为目的，留给学生自己的空间，尊重学生的爱好、个性和人格，以平等、宽容、友善的态度对待学生，形成一种民主和谐的教学环境.在民主和谐的环境中，课堂讨论能吸引学生积极主动参与，做学习的主人.

案例1   在教学“三角形内角和定理”时，教师布置学生准备两个不同形状的纸质三角形.师：这两个三角形的内角和各是多少，是否相等？生：有的摇头表示不知道，有的说都是180°.师：看来，大家的想法不一样.同学们是怎么发现它等于180°呢？请同学们小组交流、讨论.（学生讨论，师巡回指导）师：老师看各小组都有答案，哪个小组来说说你们的奇思妙想.生甲：我们用量角器分别量出三个角的度数，相加是179°.生乙：我们用量角器分别量出三个角的度数，相加是181°.生丙：我们也是用量角器分别量出三个角的度数，相加是180°.师：为什么会出现这种情况？生丁：量得不准.生戊：有的量角器有误差.师：对，这就是测量的误差，但是这些结果都比较接近于多少？生：180°.师：那到底三角形的内角和是不是180°呢？还有其它的方法进行验证吗？生甲：我们撕下三个角，把三个角拼在一起，刚好凑成一个平角，所以是180°.生乙：我们把三角形的三个内角分别往内折，也刚好凑成一个平角.师：同学们，我们刚才用不同的方法，得到了一个相同的发现，这个发现就是？生：三角形的内角和是180°.师：必须通过严格证明确定“三角形的三个内角之和是180°.”

在对定理的讨论中，师与生、生与生、组与组不断互动，学生更积极、更主动，形成一种乐于探究、不惧困难、努力求知的学习氛围，既锻炼了学生的思辨能力，又孕育了数学的求真精神.

2   立足定理探索，发展学生的演绎推理能力

演绎推理是由已知概念、定理推出新的定理的思维方式，是进行数学证明的有力工具，对数学的形成和发展有重要的作用，因此演绎推理能力是数学能力的一个重要方面.目前定理教学“轻过程、重结论”现象比较普遍，学生只是被动地接受知识，这种急于求成的教学，显然不利于学生演绎推理能力的培养.因此，我们在定理教学中，应重视定理产生、形成的过程，引导学生去探索、去发现，发展学生的演绎推理能力.

案例2   在 教学“等腰三角形的性质定理”时，提出这样的问题：将一把三角尺和重锤如图1放置，就能检查一根横梁是否水平，你知道为什么吗？学生有可能会回答“等腰三角形三线合一”，因为不能排除有部分学生已经预习，那就可以追问“等腰三角形三线为什么会合一？”使他们带着问题，带着渴望参与教学活动.教师再因势利导，与学生一起探索等腰三角形的性质定理.1.创设情境：①让学生制作一个等腰三角形纸片，对折、打开、分析;②给出一个直角三角形，让学生画出它以某一直角边为对称轴的对称图形. 2.引导学生探索：通过上面的操作实验，观察、分析、猜想，并与他人交换意见，互相讨论. 3.得出结论：①等腰三角形的两个底角相等;②等腰三角形底边上的高线、中线及顶角平分线互相重合. 4.指导学生论证：①要证两个角相等，一般的思路是什么？学生不难发现用“证明所在两个三角形全等”，进而发现必须添加辅助线，构造三角形;②让学生阐述不同的证明思路，再分别用不同的方法证明;③等腰三角形底边上的高线、中线及顶角平分线互相重合，这一命题包含3种情况，让学生一一推理论证.

对于学生来说，经历这样的探索过程，生动有趣，大大地激发了学生的求知欲和进取心，并运用学过的知识进行严谨的推理论证，发展学生的演绎推理能力.

3   立足定理研究，发展学生的合情推理能力和创新意识

3.1   直观感知，操作确认，发展学生的合情推理能力

合情推理的实质是“发现—猜想”.牛顿有一句名言：“没有大胆的猜想，就做不出伟大的发明.” [2 ]在定理教学中，鼓励学生猜想，引导学生猜想，尊重学生的猜想，让学生真正体验猜想的乐趣，享受探究的过程，进而有序地培养数学合情推理能力.

案例3：在教学“勾股定理”时，课前让每个学生准备一个以3厘米长和4厘米长为直角边的直角三角形纸片、一个以5厘米长和12厘米长为直角边的直角三角形纸片和四个全等的直角三角形纸片.先让学生量一量两个不同的直角三角形的三边的长度，并将各边的长度填入表1：

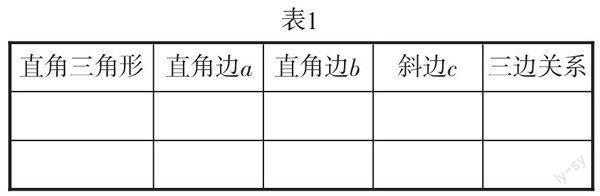
提问：根据上面表格中的数据，对于直角三角形三边的关系你有什么发现？

学生猜想：两直角边的平方和等于斜边的平方.此时，老师还不急于肯定，继续让学生探索：如图2，正方形瓷砖拼成的地面，观察图中的三个正方形有什么关系？让学生观察思考，不难发现：两个小正方形P、Q的面积之和等于大正方形R的面积，即SP+SQ=SR .

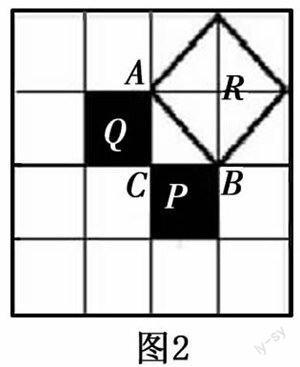
这说明Rt△ACB的三边有什么关系？

学生观察猜想：两直角边的平方和等于斜边的平方.

学生通过自己动手测量、计算和观察，从数和形两个方面得到了一个直观印象：直角三角形两直角边的平方和等于斜边的平方.这就是数学猜想！接着教师指出：猜想得出的结论，必须经过推理论证.然后因势利导，让学生拿出课前准备的4个全等的直角三角形，通过拼图，完成证明.

在定理教学中，教师不仅要充分利用教材，深入挖掘，而且还要引导学生观察、分析、探索、猜想，进而养成勇于探索、善于猜想的品质.同时教师要多鼓励少批评，鼓励学生大胆提出见解和作出猜想，激发学生的热情，培养学生的合情推理能力.

3.2   多方联想，一题多证，培养学生的发散性思维能力

发散性思维，是创造性思维的核心，对培养学生的创造力有着直接的作用.因此我们必须重视培养学生的发散性思维，在定理教学中引导学生从多角度、多方面去认识问题、分析问题、解决问题，以培养学生的发散性思维能力.

案例4：在教学“勾股定理”时，要求每个学习小组（4-6人）课前准备4个全等的直角三角形（两直角边长分别为a、b，斜边长为c）.通过动手操作、小组合作、共同探索勾股定理的证明方法.学生动手拼图、思考，教师适时引导、点拨，让学生逐渐明白数学图形的割补方法和代数恒等关系在几何中的运用，并得出多种的证明方法.下面列举其中三种证明方法：

方法1   学生用四个全等的直角三角形拼成如图3所示的正方形，利用面积相等进行证明.S大正方形=S小正方形+4S直角三角形 .

即（a+b）2=c2+4×ab，

a2+2ab+b2=c2+2ab，

故a2+b2=c2.

方法2   学生用四个全等的直角三角形拼成如图4所示的正方形，利用面积相等进行证明.

S小正方形+4S直角三角形

=S大正方形，

即（b-a）2+4×ab=c2，

b2-2ab+a2+2ab=c2，

故a2+b2=c2.

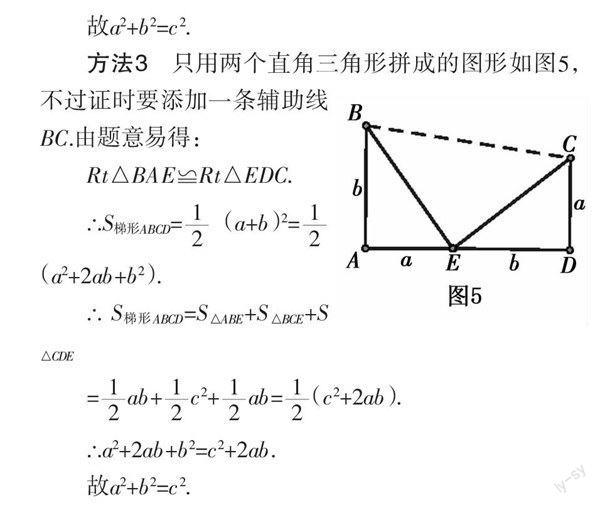
方法3   只用两个直角三角形拼成的图形如图5，不过证时要添加一条辅助线BC.由题意易得：

Rt△BAE≌Rt△EDC.

∴S梯形ABCD=（a+b）2=（a2+2ab+b2）.

∴ S梯形ABCD=S△ABE+S△BCE+S△CDE

=ab+c2+ab=（c2+2ab）.

∴a2+2ab+b2=c2+2ab.

故a2+b2=c2.

此外，教师告诉学生，勾股定理的证明方法还有很多，鼓励学生利用课余时间查阅相关资料，积极探索.

在勾股定理教学中，重视一题多证的教法，使学生在思考问题上具有灵活性、多变性，并且引导学生评价各种不同解法的特点及其优劣，这样不但能提高学生的学习兴趣，而且对于优化解题思路、增强发散思维能力有着十分积极的作用.

3.3   正难则反，正反互化，发展学生的逆向思维能力

所谓逆向思维，是指和正向思维方向相反而又相互联系的思维过程.逆向思维是思维灵活性的一种表现，是一种重要的创造性思维，在数学定理教学中，加强对学生逆向思维的培养，不仅可以让学生发现问题的解题方向，找到解题捷径，还有助于加深对定理的理解，掌握定理，使思维的灵活性和创造性得到有益的发展.

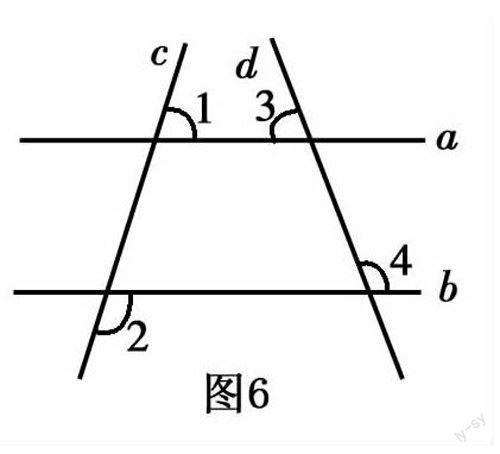
案例5   在教学“平行线的判定定理”时，教师先让学生回忆“平行线的性质”，后提出问题，反过来，得到什么？学生很容易得出对应的三个命题，经推理论证后得到平行线的判定定理.为了训练学生的思维，随即考学生一道题，如图6，∠1+∠2=180°，∠3=110°求∠4的度数.学生作答后，再引导学生分析，在图中∠1和∠2的对顶角是一对同旁内角，且和为180°，从而得出a∥b;再由两直线平行，同旁内角互补，得到∠3的对顶角与∠4互补，从而得出∠4=70°.

当然，逆向思维能力的培养不是一朝一夕的事，需要我们教师在平时的教学中多注意积累，有意识地利用各种教学的手段和方法对学生进行逆向思维的训练.

3.4   观察比较，类比联想，发展学生的求同思维能力

类比思维是从两个对象之间在某些方面的相似关系中受到启发，从而使问题得到解决的一种创造性思维. [3 ]由于类比思维具有从一个特殊领域的知识过渡到另一个特殊领域的知识的优越性，所以将类比用于定理的教学，不但可以加深学生对定理的理解和记忆，也可以使学生对所学知识有个系统化的了解，发展学生的求同思维能力.

案例6   在 教学“角平分线的性质和判定定理”时，由于它与“线段垂直平分线的性质和判定定理”有很多类似的地方，因此引导学生使用类比法.具体如下：①由“线段垂直平分线上的点与这条线段两个端点的距离相等” 类比得到“角的平分线上的点到角两边的距离相等”;②由“与一条线段两个端点距离相等的点，在这条线段的垂直平分线上”类比得到“角的内部到角的两边距离相等的点在角的平分线上”.

通过类比，以旧引新，使学生对新的定理的理解更深入、记忆更牢固，运用更灵活.在学生观察比较过程中，教师启发、引导、点拨，使学生变学为思，促进学生的求同思维能力的发展.

4   结束语

数学定理教学的根本任务不仅在于向学生传授知识，更重要的是开发学生的思维.学生思维能力的培养是多方位的，在定理教学的每个环节中，需要教师积极创设途径，通过引导和启迪，使学生参与到分析知识的形成过程中去，从而使学生的思维能力得到有效的开发和培养.只有师生共同配合，才能教学相长，才能使学生的思维在数学课堂教学中得到发展.

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准[S].北京师范大学出版社，2012.

[2]周述乾.在低年级数学教学中学生创新意识的培养[J].读与算（教研版），2014（1）.

[3]刘仁兰.类比思维在化学教学中的运用[J]. 中学时代：理论版，2013（9）.